28.1.1 正弦函数 同步练习
图片预览

文档简介
28.1.1正弦函数
基础训练
知识点1 正弦函数的定义
1.把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
2.在Rt△ABC,∠C=90°,AC=12,BC=5,则sin A的值为( )
A. B. C. D.
3.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则∠α的正弦值为( )
A. B. C. D.
4.如图,已知△ABC的外接圆O的半径为3,AC=4,则sin B=( )
A. B. C. D.
5.已知锐角A的正弦值sin A是一元二次方程2x2-7x+3=0的根,则sin A=___________.?21世纪教育网版权所有
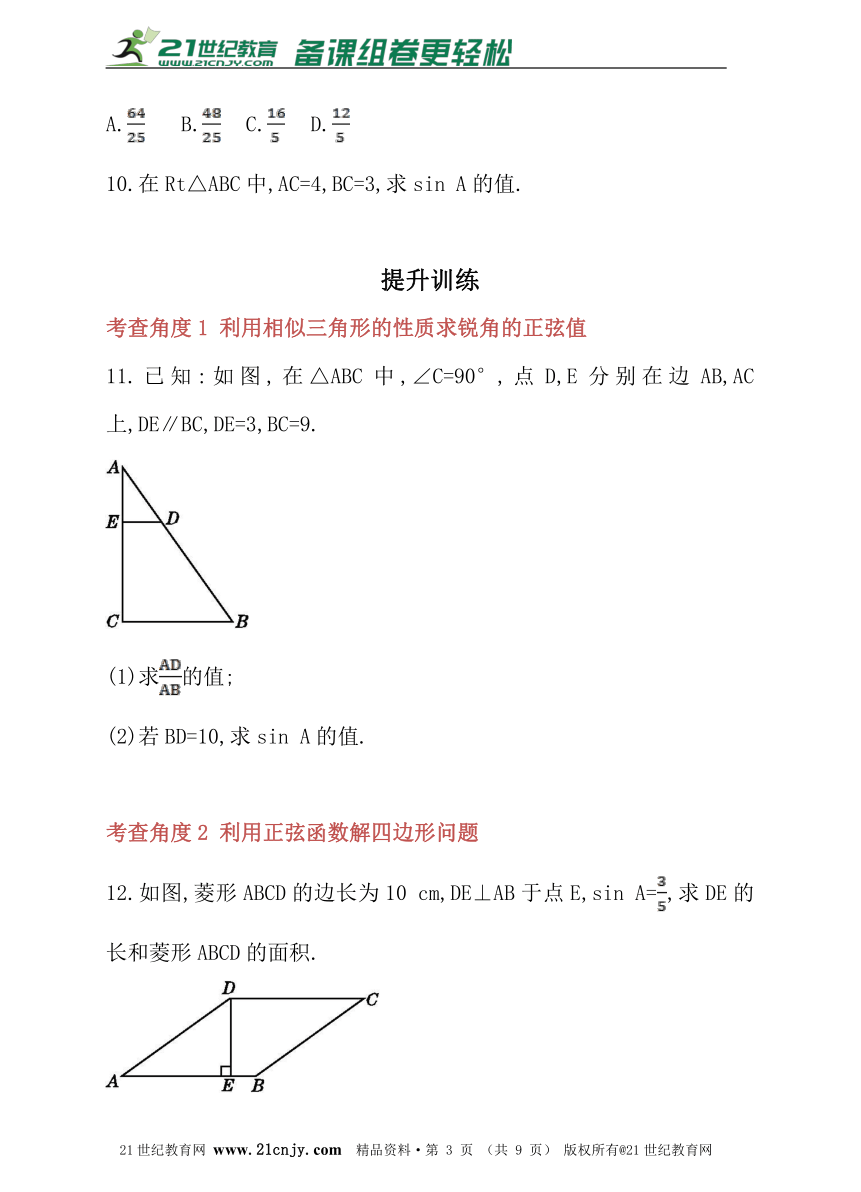
6.如图,在☉O中,过直径AB延长线上的点C作☉O的一条切线,切点为D,若AC=7,AB=4,则sin C的值为___________.www.21-cn-jy.com
知识点2 正弦函数的应用
7.如图,∠α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(b,4),若sin α=,则b= .21·cn·jy·com
8.在Rt△ABC中,∠C=90°,AC=9,sin B=,则AB等于( )
A.15 B.12 C.9 D.6
9.在Rt△ABC中,∠C=90°,若AB=4,sin A=,则斜边上的高等于( )
A. B. C. D.
10.在Rt△ABC中,AC=4,BC=3,求sin A的值.
提升训练
考查角度1 利用相似三角形的性质求锐角的正弦值
11.已知:如图,在△ABC中,∠C=90°,点D,E分别在边AB,AC上,DE∥BC,DE=3,BC=9.2·1·c·n·j·y
(1)求的值;
(2)若BD=10,求sin A的值.
考查角度2 利用正弦函数解四边形问题
12.如图,菱形ABCD的边长为10 cm,DE⊥AB于点E,sin A=,求DE的长和菱形ABCD的面积.【来源:21·世纪·教育·网】
考查角度3 利用正弦函数解一次函数、反比例函数问题
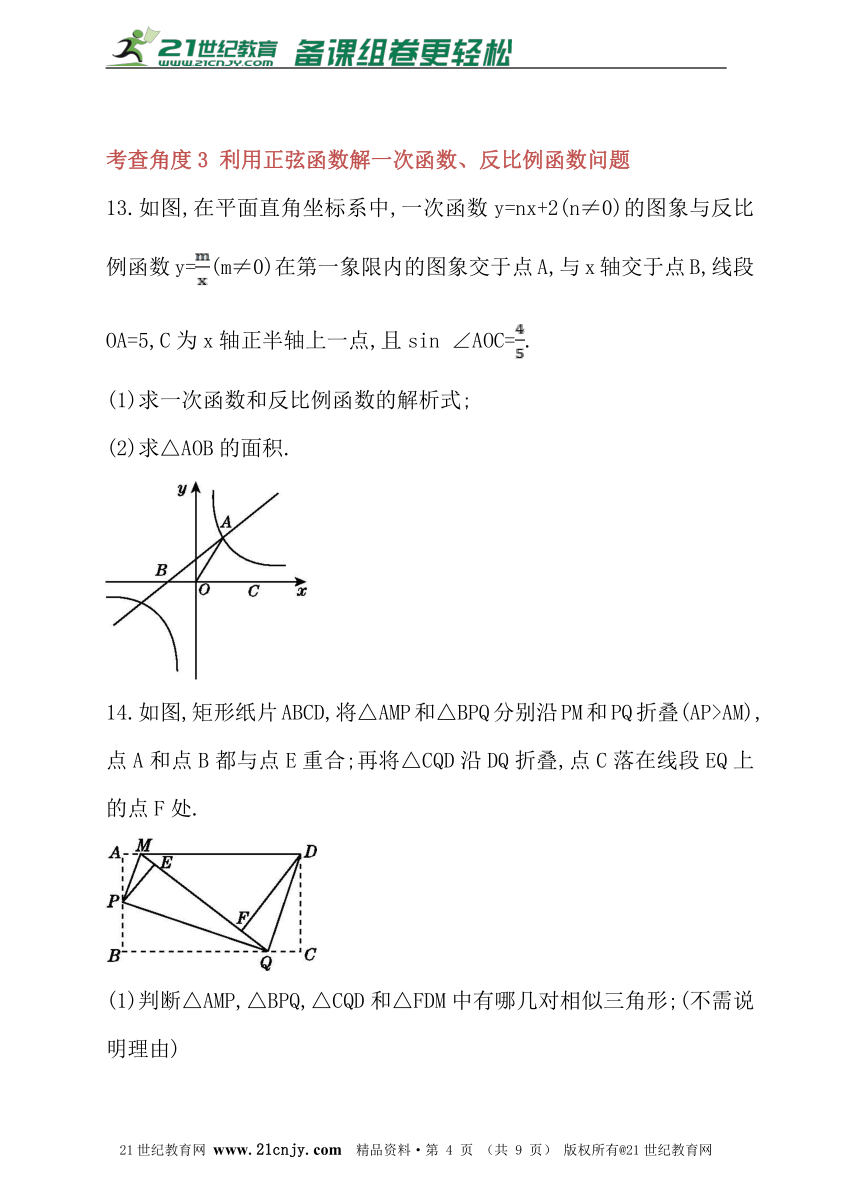
13.如图,在平面直角坐标系中,一次函数y=nx+2(n≠0)的图象与反比例函数y=(m≠0)在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且sin ∠AOC=.21·世纪*教育网
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
14.如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上的点F处.www-2-1-cnjy-com
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形;(不需说明理由)
(2)如果AM=1,sin ∠DMF=,求AB的长.
15.如图,已知☉O的直径AB为3,线段AC=4,直线AC和PM分别与☉O相切于点A,M.
(1)求证:点P是线段AC的中点;
(2)求sin ∠PMC的值.
参考答案
1.【答案】A 2.【答案】D 3.【答案】A
4.【答案】D 5.【答案】
6.【答案】
解:如图,连接OD,∵CD是☉O的切线,∴∠ODC=90°.
∵AC=7,AB=4,∴BC=3,OB=OD=OA=2,
∴OC=5.在Rt△ODC中,sin C==.
7.【答案】3 8.【答案】A 9.【答案】B
10.解:此题分两种情况:①当AC,BC为两直角边时,AB===5,所以sin A==;②当BC为直角边,AC为斜边时,sin A==.21cnjy.com
解:学生往往误认为∠C是直角,AC,BC是两直角边,从而漏掉一个值.
11.解:(1)∵DE∥BC,∴△ADE∽△ABC,∴=.
又∵DE=3,BC=9,∴==.
(2)根据(1)=,得:=.∵BD=10,DE=3,BC=9,
∴=,解得AD=5,∴AB=15.
∴sin A===.
12.解:∵DE⊥AB,∴∠AED=90°,∴sin A==,
∴DE=sin A·AD=×10=6(cm).
∴S菱形ABCD=AB·DE=10×6=60(cm2).
13.解:(1)过点A作AD⊥x轴于点D.
∵sin ∠AOC==,OA=5,∴AD=4,则DO==3.
∵点A在第一象限,∴点A坐标为(3,4).将A(3,4)代入y=,解得m=12,∴反比例函数解析式为y=.将A(3,4)代入y=nx+2,解得n=,∴一次函数解析式为y=x+2.21教育网
(2)∵一次函数y=x+2的图象与x轴交于点B,∴0=x+2,解得x=-3,
∴B点坐标为(-3,0).
∴S△AOB=OB·AD=×3×4=6.
14.解:(1)△AMP∽△BPQ∽△CQD,共3对.
(2)∵AD∥BC,
∴∠DQC=∠MDQ,
根据折叠的性质可知:∠DQC=∠DQM,
∴∠MDQ=∠DQM,
∴MD=MQ.
∵AM=ME,BQ=EQ,
∴BQ=MQ-ME=MD-AM.
∵sin ∠DMF==,
∴设DF=3x,MD=5x,
∴BP=PE=PA=,BQ=5x-1.
∵△AMP∽△BPQ,
∴=,
∴=,
解得:x=或x=2.∵当x=时,AP=x=∴x=应舍去.
∴AB=AP+BP=3x=6.
15.(1)证明:如图,连接AM.
∵AB是☉O的直径,
∴∠AMB=90°,
∴∠AMC=90°.
∴∠MAC+∠C=90°,∠PMC+∠PMA=90°.
∵AC和PM分别与☉O相切于点A,M,
∴PM=PA.
∴∠PMA=∠PAM.
∴∠C=∠PMC.
∴PC=PM.
∴PA=PC,即点P是线段AC的中点.
(2)解:∵AC切☉O于点A,
∴∠BAC=90°.
又∵AB=3,AC=4,∴BC=5.
由(1)知∠C=∠PMC,
∴sin ∠PMC=sin C==.
基础训练
知识点1 正弦函数的定义
1.把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
2.在Rt△ABC,∠C=90°,AC=12,BC=5,则sin A的值为( )
A. B. C. D.
3.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则∠α的正弦值为( )
A. B. C. D.
4.如图,已知△ABC的外接圆O的半径为3,AC=4,则sin B=( )
A. B. C. D.
5.已知锐角A的正弦值sin A是一元二次方程2x2-7x+3=0的根,则sin A=___________.?21世纪教育网版权所有
6.如图,在☉O中,过直径AB延长线上的点C作☉O的一条切线,切点为D,若AC=7,AB=4,则sin C的值为___________.www.21-cn-jy.com
知识点2 正弦函数的应用
7.如图,∠α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(b,4),若sin α=,则b= .21·cn·jy·com
8.在Rt△ABC中,∠C=90°,AC=9,sin B=,则AB等于( )
A.15 B.12 C.9 D.6
9.在Rt△ABC中,∠C=90°,若AB=4,sin A=,则斜边上的高等于( )
A. B. C. D.
10.在Rt△ABC中,AC=4,BC=3,求sin A的值.
提升训练
考查角度1 利用相似三角形的性质求锐角的正弦值
11.已知:如图,在△ABC中,∠C=90°,点D,E分别在边AB,AC上,DE∥BC,DE=3,BC=9.2·1·c·n·j·y
(1)求的值;
(2)若BD=10,求sin A的值.
考查角度2 利用正弦函数解四边形问题
12.如图,菱形ABCD的边长为10 cm,DE⊥AB于点E,sin A=,求DE的长和菱形ABCD的面积.【来源:21·世纪·教育·网】
考查角度3 利用正弦函数解一次函数、反比例函数问题
13.如图,在平面直角坐标系中,一次函数y=nx+2(n≠0)的图象与反比例函数y=(m≠0)在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且sin ∠AOC=.21·世纪*教育网
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
14.如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上的点F处.www-2-1-cnjy-com
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形;(不需说明理由)
(2)如果AM=1,sin ∠DMF=,求AB的长.
15.如图,已知☉O的直径AB为3,线段AC=4,直线AC和PM分别与☉O相切于点A,M.
(1)求证:点P是线段AC的中点;
(2)求sin ∠PMC的值.
参考答案
1.【答案】A 2.【答案】D 3.【答案】A
4.【答案】D 5.【答案】
6.【答案】
解:如图,连接OD,∵CD是☉O的切线,∴∠ODC=90°.
∵AC=7,AB=4,∴BC=3,OB=OD=OA=2,
∴OC=5.在Rt△ODC中,sin C==.
7.【答案】3 8.【答案】A 9.【答案】B
10.解:此题分两种情况:①当AC,BC为两直角边时,AB===5,所以sin A==;②当BC为直角边,AC为斜边时,sin A==.21cnjy.com
解:学生往往误认为∠C是直角,AC,BC是两直角边,从而漏掉一个值.
11.解:(1)∵DE∥BC,∴△ADE∽△ABC,∴=.
又∵DE=3,BC=9,∴==.
(2)根据(1)=,得:=.∵BD=10,DE=3,BC=9,
∴=,解得AD=5,∴AB=15.
∴sin A===.
12.解:∵DE⊥AB,∴∠AED=90°,∴sin A==,
∴DE=sin A·AD=×10=6(cm).
∴S菱形ABCD=AB·DE=10×6=60(cm2).
13.解:(1)过点A作AD⊥x轴于点D.
∵sin ∠AOC==,OA=5,∴AD=4,则DO==3.
∵点A在第一象限,∴点A坐标为(3,4).将A(3,4)代入y=,解得m=12,∴反比例函数解析式为y=.将A(3,4)代入y=nx+2,解得n=,∴一次函数解析式为y=x+2.21教育网
(2)∵一次函数y=x+2的图象与x轴交于点B,∴0=x+2,解得x=-3,
∴B点坐标为(-3,0).
∴S△AOB=OB·AD=×3×4=6.
14.解:(1)△AMP∽△BPQ∽△CQD,共3对.
(2)∵AD∥BC,
∴∠DQC=∠MDQ,
根据折叠的性质可知:∠DQC=∠DQM,
∴∠MDQ=∠DQM,
∴MD=MQ.
∵AM=ME,BQ=EQ,
∴BQ=MQ-ME=MD-AM.
∵sin ∠DMF==,
∴设DF=3x,MD=5x,
∴BP=PE=PA=,BQ=5x-1.
∵△AMP∽△BPQ,
∴=,
∴=,
解得:x=或x=2.∵当x=时,AP=x=
∴AB=AP+BP=3x=6.
15.(1)证明:如图,连接AM.
∵AB是☉O的直径,
∴∠AMB=90°,
∴∠AMC=90°.
∴∠MAC+∠C=90°,∠PMC+∠PMA=90°.
∵AC和PM分别与☉O相切于点A,M,
∴PM=PA.
∴∠PMA=∠PAM.
∴∠C=∠PMC.
∴PC=PM.
∴PA=PC,即点P是线段AC的中点.
(2)解:∵AC切☉O于点A,
∴∠BAC=90°.
又∵AB=3,AC=4,∴BC=5.
由(1)知∠C=∠PMC,
∴sin ∠PMC=sin C==.
