28.1.2 余弦、正切函数 同步练习
文档属性
| 名称 | 28.1.2 余弦、正切函数 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 616.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-02 00:00:00 | ||
图片预览

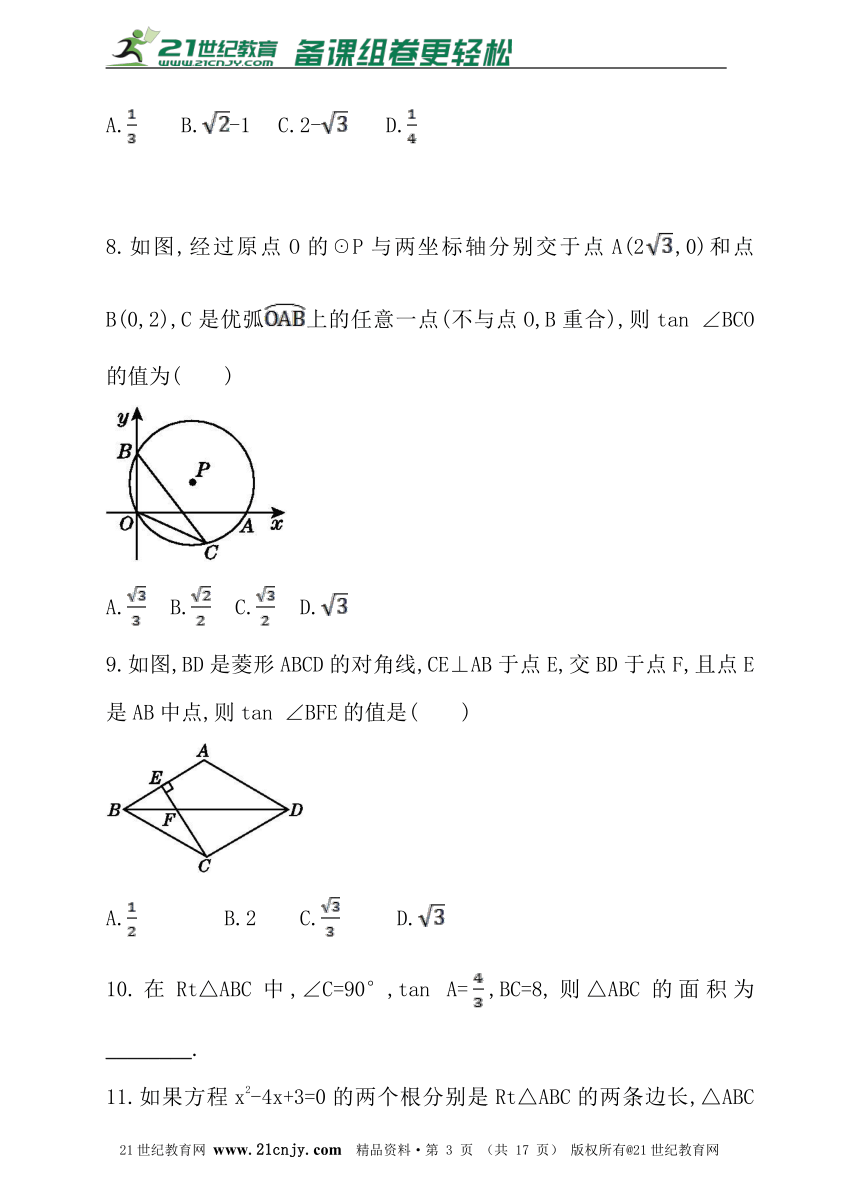

文档简介
28.1.2 余弦、正切函数
基础训练
知识点1 余弦函数
1.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,那么cos A的值等于( )
A. B. C. D.
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cos α的值,错误的是( )21*cnjy*com
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若sin A=,则cos B的值是( )
A. B. C. D.
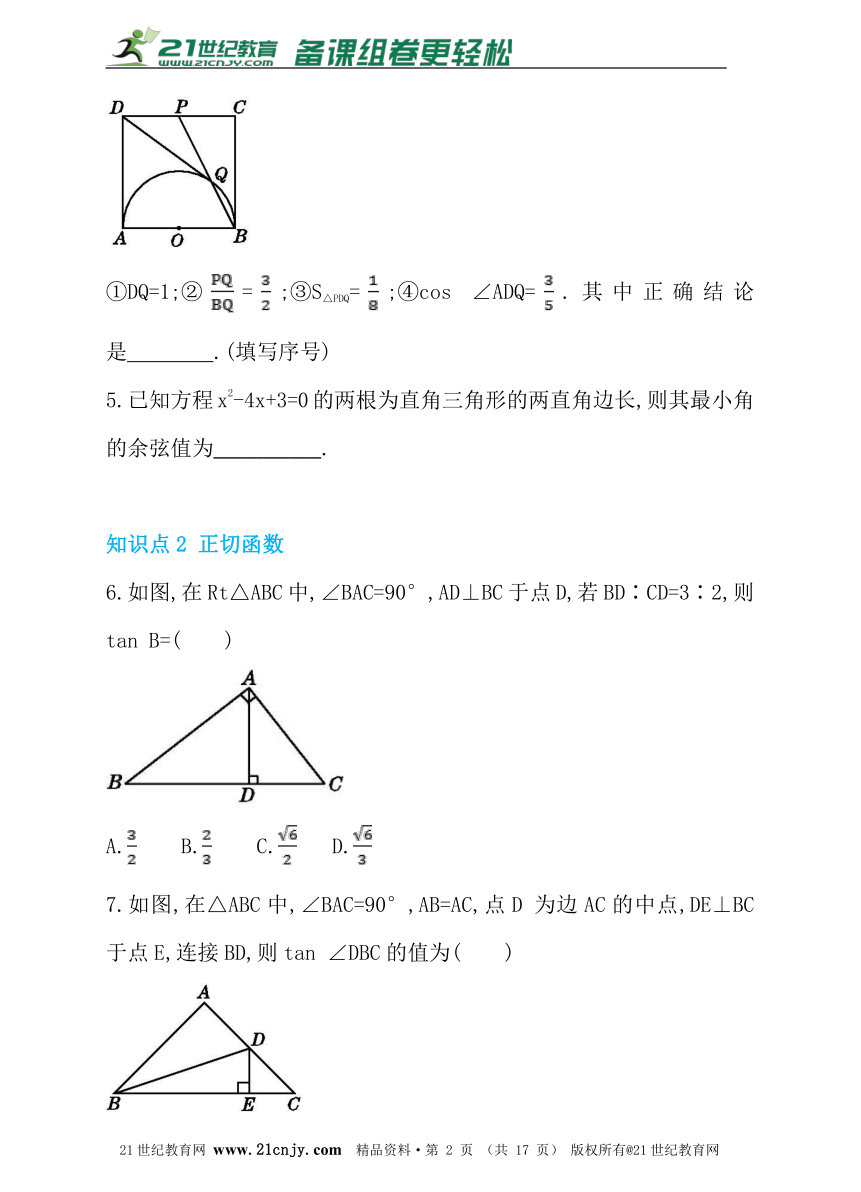
4.如图,正方形ABCD边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连接DQ.给出如下结论:
①DQ=1;②=;③S△PDQ=;④cos ∠ADQ=.其中正确结论是 .(填写序号)?
5.已知方程x2-4x+3=0的两根为直角三角形的两直角边长,则其最小角的余弦值为__________.
知识点2 正切函数
6.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tan B=( )
A. B. C. D.
7.如图,在△ABC中,∠BAC=90°,AB=AC,点D 为边AC的中点,DE⊥BC于点E,连接BD,则tan ∠DBC的值为( )
A. B.-1 C.2- D.
8.如图,经过原点O的☉P与两坐标轴分别交于点A(2,0)和点B(0,2),C是优弧上的任意一点(不与点O,B重合),则tan ∠BCO的值为( )
A. B. C. D.
9.如图,BD是菱形ABCD的对角线,CE⊥AB于点E,交BD于点F,且点E是AB中点,则tan ∠BFE的值是( )21·世纪*教育网
A. B.2 C. D.
10.在Rt△ABC中,∠C=90°,tan A=,BC=8,则△ABC的面积为________.?
11.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC最小的角为∠A,那么tan A的值为________.?
12.在△ABC中,∠C=90°,若把AB,BC都扩大为原来的m倍,则cos B的值是( )
A.mcosB B.cos B C. D.不变
13.已知x=cos α(α为锐角)满足方程2x2-5x+2=0,求cos α的值.
提升训练
考查角度1 利用三角函数定义求锐角三角函数值(定义法)
14.如图,在Rt△ABC中,∠C=90°,AC=2,AB=3,求sin A,cos A,tan A的值.21cnjy.com
考查角度2 利用三角函数定义证明锐角三角函数之间的关系
15.已知∠A为锐角,
证明:(1)sin A=cos (90°-∠A);
(2)sin2 A+cos2 A=1;
(3)tan A=.
考查角度3 利用三角函数定义巧求三角函数值
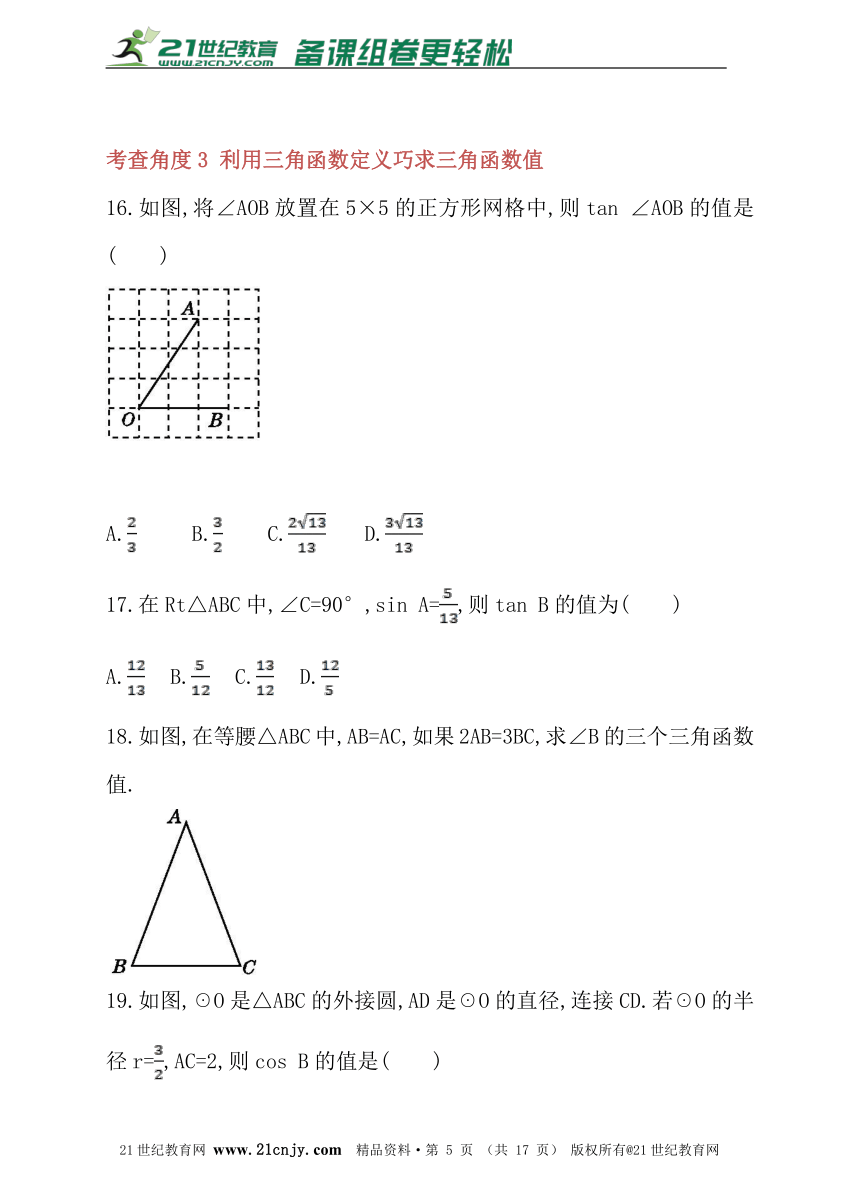
16.如图,将∠AOB放置在5×5的正方形网格中,则tan ∠AOB的值是( )
A. B. C. D.
17.在Rt△ABC中,∠C=90°,sin A=,则tan B的值为( )
A. B. C. D.
18.如图,在等腰△ABC中,AB=AC,如果2AB=3BC,求∠B的三个三角函数值.
19.如图,☉O是△ABC的外接圆,AD是☉O的直径,连接CD.若☉O的半径r=,AC=2,则cos B的值是( )21教育网
A. B. C. D.
考查角度4 利用三角函数解折叠问题(折叠法)
20.如图,E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin ∠DFE=,求tan ∠EBC的值.
21.如图,已知锐角三角形ABC.
(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若BC=5,AD=4,tan ∠BAD=,求DC的长.
22.如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cos A=.【来源:21·世纪·教育·网】
(1)求线段CD的长;
(2)求sin ∠DBE的值.
探究培优
拔尖角度1 利用三角函数解与圆有关的综合问题
23.如图,AB是☉O的直径,点C在☉O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是☉O的切线;
(2)若=,求cos ∠ABC的值.
拔尖角度2 利用构造相似三角形求三角函数值(构造法)
24.已知线段OA⊥OB,C为OB的中点,D为AO上一点,连接AC,BD交于点P.
(1)如图①,当OA=OB,且D为AO的中点时,求的值;
(2)如图②,当OA=OB,=时,求tan ∠BPC的值.
参考答案
1.【答案】D 2.【答案】C 3.【答案】B
4.【答案】①②④
5.【答案】
解:先求出方程x2-4x+3=0的两根,即可得到两直角边长,再根据勾股定理求得斜边长,最后根据余弦的定义即可求得结果.解方程x2-4x+3=0,得x1=1,x2=3,www-2-1-cnjy-com
则直角三角形的两直角边长分别为1,3,斜边长为=.故其最小角的余弦值为=.
6.【答案】D
解:在Rt△ABC中,∵AD⊥BC于点D,∴∠ADB=∠CDA=90°,
∴∠B+∠BAD=90°.
又∵∠BAD+∠DAC=90°,
∴∠B=∠DAC.∴△ABD∽△CAD,
∴=.∵BD∶CD=3∶2,∴设BD=3x(x>0),则
CD=2x,∴AD==x,则tan B===.故选D.
7.【答案】A 8.【答案】A 9.【答案】D
10.【答案】24
11.【答案】或
12.【答案】D
解:∵cos B==,∴cos B的值不变.
常见错解:误认为∠B的邻边与斜边都扩大为原来的m倍,则cos B也扩大为原来的m倍,而错选A,实际上cos B的值只与∠B的大小有关,与∠B的两边长短无关.2·1·c·n·j·y
13.解:∵方程2x2-5x+2=0的解是x1=2,x2=,
又∵0常见错解:∵方程2x2-5x+2=0的解是x1=2,x2=,
此时忽略了cos α(α为锐角)的取值范围是014.解:∵△ABC是直角三角形,
∴根据勾股定理,得BC===.
∴sin A==,
cos A==,
tan A==.
方法解:在直角三角形中,只要已知直角三角形的任意两边,根据勾股定理,可求出第三边,然后根据锐角三角函数的定义,可求出该直角三角形中任意一个锐角的正弦、余弦及正切值.21·cn·jy·com
15.证明:作Rt△ABC,使∠C=90°,如图,
则sin A=,cos A=,
tan A=.
(1)∵cos B=,sin A=,
∴sin A=cos B.
又∵∠A+∠B=90°,∴∠B=90°-∠A,
∴sin A=cos (90°-∠A).
(2)∵sin A=,cos A=,且a2+b2=c2,
∴sin2A+cos2A=+===1.
(3)∵sin A=,cos A=,
∴==.
又∵tan A=,∴tan A=.
16.【答案】B
解:在OB上距点O 2格的位置上取一点,并过该点作OB的垂线,得到一个直角三角形.在该直角三角形中,∠AOB的对边长为3,邻边长为2,所以tan ∠AOB=.故选B.【来源:21cnj*y.co*m】
方法总结:用定义法求锐角三角函数值时,要注意以下两点:(1)要判断这个角所在的三角形的形状,只有在直角三角形中才能利用定义;(2)在直角三角形中求边时,注意勾股定理的应用.此题在图中找“格点”构建直角三角形是关键.【出处:21教育名师】
17.【答案】D
解:如图,sin A==, 可设BC=5k,AB=13k,用勾股定理可求AC==12k.
∴tan B===.
方法总结:已知直角三角形中一个锐角的某个三角函数值,求这个锐角和它的余角的其他三角函数值,可先画出直角三角形,结合图形和已知条件,可利用“设k法”,将直角三角形的各边长用含k的代数式表示,然后根据锐角三角函数的定义,求得锐角的三角函数值.
18.解:过点A作AD⊥BC于点D,如图所示.
∵AB=AC,
∴BD=CD.
又∵2AB=3BC,∴=.
设AB=AC=3k,则BC=2k.
∴BD=CD=k,
∴AD====2k.
∴sin B===,cos B===,
tan B===2.
方法总结:求某一锐角的三角函数值时,正确地构造直角三角形是解题的关键.若已知其中两边的比值或倍数关系,可将这两边设出,再利用勾股定理表示出第三条边,则这个锐角的任一个三角函数值都可求出.
19.【答案】B
解:欲求cos B的值,必须将∠B放在直角三角形中去求,由题图可知,∠B与∠D是同弧所对的圆周角,∴∠B=∠D.∵AD是☉O的直径,∴∠ACD=90°,通过等角转化即求cos D的值.在Rt△ACD中,AC=2,AD=2r=3,由勾股定理可求得CD=,∴cos B=cos D==.21*cnjy*com
20.(1)证明:由题意可得∠A=∠D=∠C=∠BFE=90°,
∴∠ABF=90°-∠AFB,
∠DFE=180°-∠BFE-∠AFB=90°-∠AFB=∠ABF,
∴△ABF∽△DFE.
(2)解:由折叠可得FB=BC,EF=EC,∵sin ∠DFE=,
∴=,即
EF=3DE.∴AB=CD=DE+EC=DE+EF=4DE,DF==DE×=2DE.
∵△ABF∽△DFE,∴=,即FB===3DE.又∵FB=BC,EF=EC,∴tan ∠EBC====.【版权所有:21教育】
21.解:(1)如图,MN为所作.
(2)在Rt△ABD中,tan ∠BAD==,
∴=,
∴BD=3.
∴DC=BC-BD=5-3=2.
22.解:(1)∵AC=15,cos A=,
∴cos A===,
∴AB=25.
∵△ACB为直角三角形,点D是斜边AB的中点,
∴CD=AB=.
(2)∵BC2=AB2-AC2=252-152=400,AD=BD=CD=,
∴设DE=x,EB=y,
则解得x=.
∴sin ∠DBE===.
解:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长.(2)由于点D为AB边的中点,则AD=BD=CD=.设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
23.(1)证明:连接OC.
∵AD是过点A的切线,AB是☉O的直径,
∴AD⊥AB,∴∠DAB=90°.
∵OD∥BC,
∴∠DOC=∠OCB,∠AOD=∠ABC.
∵OC=OB,∴∠OCB=∠ABC,
∴∠DOC=∠AOD.
在△COD和△AOD中,
∴△COD≌△AOD.
∴∠OCD=∠DAB=90°.
∵OC⊥DE于点C,OC是☉O的半径,
∴DE是☉O的切线.
(2)解:由=,可设CE=2k,则DE=3k,
又∵AD,CD都是☉O的切线,
∴AD=DC=k.
在Rt△DAE中,AE==2k.
∵OD∥BC,=,
∴BE=2OB.
∴OA=AE=k.
∴在Rt△AOD中,OD==k=k,
∴cos ∠ABC=cos ∠AOD==.
24.解:(1)过点C作CE∥OA 交BD于点E,∴△BCE∽△BOD.∵C为OB中点,D为AO中点,∴CE=OD=AD.21世纪教育网版权所有
∵CE∥AD,∴△ECP∽△DAP,∴==2.
(2)过点C作CE∥OA交BD于点E.设AD=x,∵OA=OB,=,则AO=OB=4x,OD=3x.∵CE∥OD,∴△BCE∽△BOD,∴CE=OD=x.∵CE∥AD,∴△ECP∽△DAP,∴==.由勾股定理可知BD=5x,则DE=BD=x.∴===,解得PD=x,∴PD=AD.www.21-cn-jy.com
∴∠BPC=∠DPA=∠A.∵OA=OB,C是OB中点,∴CO=OB=AO,
∴tan ∠BPC=tan A==.
分析:看到线段成比例时,一定要想到相似三角形的对应边成比例,如果图形中没有相似三角形,常常用到的辅助线是作平行线构造相似三角形.求一个锐角的正切值时一定要在直角三角形中进行,如果该角不在直角三角形中,可以利用相等的角进行转换.21教育名师原创作品
基础训练
知识点1 余弦函数
1.如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,那么cos A的值等于( )
A. B. C. D.
2.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cos α的值,错误的是( )21*cnjy*com
A. B. C. D.
3.在Rt△ABC中,∠C=90°,若sin A=,则cos B的值是( )
A. B. C. D.
4.如图,正方形ABCD边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连接DQ.给出如下结论:
①DQ=1;②=;③S△PDQ=;④cos ∠ADQ=.其中正确结论是 .(填写序号)?
5.已知方程x2-4x+3=0的两根为直角三角形的两直角边长,则其最小角的余弦值为__________.
知识点2 正切函数
6.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tan B=( )
A. B. C. D.
7.如图,在△ABC中,∠BAC=90°,AB=AC,点D 为边AC的中点,DE⊥BC于点E,连接BD,则tan ∠DBC的值为( )
A. B.-1 C.2- D.
8.如图,经过原点O的☉P与两坐标轴分别交于点A(2,0)和点B(0,2),C是优弧上的任意一点(不与点O,B重合),则tan ∠BCO的值为( )
A. B. C. D.
9.如图,BD是菱形ABCD的对角线,CE⊥AB于点E,交BD于点F,且点E是AB中点,则tan ∠BFE的值是( )21·世纪*教育网
A. B.2 C. D.
10.在Rt△ABC中,∠C=90°,tan A=,BC=8,则△ABC的面积为________.?
11.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边长,△ABC最小的角为∠A,那么tan A的值为________.?
12.在△ABC中,∠C=90°,若把AB,BC都扩大为原来的m倍,则cos B的值是( )
A.mcosB B.cos B C. D.不变
13.已知x=cos α(α为锐角)满足方程2x2-5x+2=0,求cos α的值.
提升训练
考查角度1 利用三角函数定义求锐角三角函数值(定义法)
14.如图,在Rt△ABC中,∠C=90°,AC=2,AB=3,求sin A,cos A,tan A的值.21cnjy.com
考查角度2 利用三角函数定义证明锐角三角函数之间的关系
15.已知∠A为锐角,
证明:(1)sin A=cos (90°-∠A);
(2)sin2 A+cos2 A=1;
(3)tan A=.
考查角度3 利用三角函数定义巧求三角函数值
16.如图,将∠AOB放置在5×5的正方形网格中,则tan ∠AOB的值是( )
A. B. C. D.
17.在Rt△ABC中,∠C=90°,sin A=,则tan B的值为( )
A. B. C. D.
18.如图,在等腰△ABC中,AB=AC,如果2AB=3BC,求∠B的三个三角函数值.
19.如图,☉O是△ABC的外接圆,AD是☉O的直径,连接CD.若☉O的半径r=,AC=2,则cos B的值是( )21教育网
A. B. C. D.
考查角度4 利用三角函数解折叠问题(折叠法)
20.如图,E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin ∠DFE=,求tan ∠EBC的值.
21.如图,已知锐角三角形ABC.
(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若BC=5,AD=4,tan ∠BAD=,求DC的长.
22.如图,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cos A=.【来源:21·世纪·教育·网】
(1)求线段CD的长;
(2)求sin ∠DBE的值.
探究培优
拔尖角度1 利用三角函数解与圆有关的综合问题
23.如图,AB是☉O的直径,点C在☉O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是☉O的切线;
(2)若=,求cos ∠ABC的值.
拔尖角度2 利用构造相似三角形求三角函数值(构造法)
24.已知线段OA⊥OB,C为OB的中点,D为AO上一点,连接AC,BD交于点P.
(1)如图①,当OA=OB,且D为AO的中点时,求的值;
(2)如图②,当OA=OB,=时,求tan ∠BPC的值.
参考答案
1.【答案】D 2.【答案】C 3.【答案】B
4.【答案】①②④
5.【答案】
解:先求出方程x2-4x+3=0的两根,即可得到两直角边长,再根据勾股定理求得斜边长,最后根据余弦的定义即可求得结果.解方程x2-4x+3=0,得x1=1,x2=3,www-2-1-cnjy-com
则直角三角形的两直角边长分别为1,3,斜边长为=.故其最小角的余弦值为=.
6.【答案】D
解:在Rt△ABC中,∵AD⊥BC于点D,∴∠ADB=∠CDA=90°,
∴∠B+∠BAD=90°.
又∵∠BAD+∠DAC=90°,
∴∠B=∠DAC.∴△ABD∽△CAD,
∴=.∵BD∶CD=3∶2,∴设BD=3x(x>0),则
CD=2x,∴AD==x,则tan B===.故选D.
7.【答案】A 8.【答案】A 9.【答案】D
10.【答案】24
11.【答案】或
12.【答案】D
解:∵cos B==,∴cos B的值不变.
常见错解:误认为∠B的邻边与斜边都扩大为原来的m倍,则cos B也扩大为原来的m倍,而错选A,实际上cos B的值只与∠B的大小有关,与∠B的两边长短无关.2·1·c·n·j·y
13.解:∵方程2x2-5x+2=0的解是x1=2,x2=,
又∵0
此时忽略了cos α(α为锐角)的取值范围是0
∴根据勾股定理,得BC===.
∴sin A==,
cos A==,
tan A==.
方法解:在直角三角形中,只要已知直角三角形的任意两边,根据勾股定理,可求出第三边,然后根据锐角三角函数的定义,可求出该直角三角形中任意一个锐角的正弦、余弦及正切值.21·cn·jy·com
15.证明:作Rt△ABC,使∠C=90°,如图,
则sin A=,cos A=,
tan A=.
(1)∵cos B=,sin A=,
∴sin A=cos B.
又∵∠A+∠B=90°,∴∠B=90°-∠A,
∴sin A=cos (90°-∠A).
(2)∵sin A=,cos A=,且a2+b2=c2,
∴sin2A+cos2A=+===1.
(3)∵sin A=,cos A=,
∴==.
又∵tan A=,∴tan A=.
16.【答案】B
解:在OB上距点O 2格的位置上取一点,并过该点作OB的垂线,得到一个直角三角形.在该直角三角形中,∠AOB的对边长为3,邻边长为2,所以tan ∠AOB=.故选B.【来源:21cnj*y.co*m】
方法总结:用定义法求锐角三角函数值时,要注意以下两点:(1)要判断这个角所在的三角形的形状,只有在直角三角形中才能利用定义;(2)在直角三角形中求边时,注意勾股定理的应用.此题在图中找“格点”构建直角三角形是关键.【出处:21教育名师】
17.【答案】D
解:如图,sin A==, 可设BC=5k,AB=13k,用勾股定理可求AC==12k.
∴tan B===.
方法总结:已知直角三角形中一个锐角的某个三角函数值,求这个锐角和它的余角的其他三角函数值,可先画出直角三角形,结合图形和已知条件,可利用“设k法”,将直角三角形的各边长用含k的代数式表示,然后根据锐角三角函数的定义,求得锐角的三角函数值.
18.解:过点A作AD⊥BC于点D,如图所示.
∵AB=AC,
∴BD=CD.
又∵2AB=3BC,∴=.
设AB=AC=3k,则BC=2k.
∴BD=CD=k,
∴AD====2k.
∴sin B===,cos B===,
tan B===2.
方法总结:求某一锐角的三角函数值时,正确地构造直角三角形是解题的关键.若已知其中两边的比值或倍数关系,可将这两边设出,再利用勾股定理表示出第三条边,则这个锐角的任一个三角函数值都可求出.
19.【答案】B
解:欲求cos B的值,必须将∠B放在直角三角形中去求,由题图可知,∠B与∠D是同弧所对的圆周角,∴∠B=∠D.∵AD是☉O的直径,∴∠ACD=90°,通过等角转化即求cos D的值.在Rt△ACD中,AC=2,AD=2r=3,由勾股定理可求得CD=,∴cos B=cos D==.21*cnjy*com
20.(1)证明:由题意可得∠A=∠D=∠C=∠BFE=90°,
∴∠ABF=90°-∠AFB,
∠DFE=180°-∠BFE-∠AFB=90°-∠AFB=∠ABF,
∴△ABF∽△DFE.
(2)解:由折叠可得FB=BC,EF=EC,∵sin ∠DFE=,
∴=,即
EF=3DE.∴AB=CD=DE+EC=DE+EF=4DE,DF==DE×=2DE.
∵△ABF∽△DFE,∴=,即FB===3DE.又∵FB=BC,EF=EC,∴tan ∠EBC====.【版权所有:21教育】
21.解:(1)如图,MN为所作.
(2)在Rt△ABD中,tan ∠BAD==,
∴=,
∴BD=3.
∴DC=BC-BD=5-3=2.
22.解:(1)∵AC=15,cos A=,
∴cos A===,
∴AB=25.
∵△ACB为直角三角形,点D是斜边AB的中点,
∴CD=AB=.
(2)∵BC2=AB2-AC2=252-152=400,AD=BD=CD=,
∴设DE=x,EB=y,
则解得x=.
∴sin ∠DBE===.
解:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长.(2)由于点D为AB边的中点,则AD=BD=CD=.设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
23.(1)证明:连接OC.
∵AD是过点A的切线,AB是☉O的直径,
∴AD⊥AB,∴∠DAB=90°.
∵OD∥BC,
∴∠DOC=∠OCB,∠AOD=∠ABC.
∵OC=OB,∴∠OCB=∠ABC,
∴∠DOC=∠AOD.
在△COD和△AOD中,
∴△COD≌△AOD.
∴∠OCD=∠DAB=90°.
∵OC⊥DE于点C,OC是☉O的半径,
∴DE是☉O的切线.
(2)解:由=,可设CE=2k,则DE=3k,
又∵AD,CD都是☉O的切线,
∴AD=DC=k.
在Rt△DAE中,AE==2k.
∵OD∥BC,=,
∴BE=2OB.
∴OA=AE=k.
∴在Rt△AOD中,OD==k=k,
∴cos ∠ABC=cos ∠AOD==.
24.解:(1)过点C作CE∥OA 交BD于点E,∴△BCE∽△BOD.∵C为OB中点,D为AO中点,∴CE=OD=AD.21世纪教育网版权所有
∵CE∥AD,∴△ECP∽△DAP,∴==2.
(2)过点C作CE∥OA交BD于点E.设AD=x,∵OA=OB,=,则AO=OB=4x,OD=3x.∵CE∥OD,∴△BCE∽△BOD,∴CE=OD=x.∵CE∥AD,∴△ECP∽△DAP,∴==.由勾股定理可知BD=5x,则DE=BD=x.∴===,解得PD=x,∴PD=AD.www.21-cn-jy.com
∴∠BPC=∠DPA=∠A.∵OA=OB,C是OB中点,∴CO=OB=AO,
∴tan ∠BPC=tan A==.
分析:看到线段成比例时,一定要想到相似三角形的对应边成比例,如果图形中没有相似三角形,常常用到的辅助线是作平行线构造相似三角形.求一个锐角的正切值时一定要在直角三角形中进行,如果该角不在直角三角形中,可以利用相等的角进行转换.21教育名师原创作品
