8.2.2多项式与多项式相乘同步练习
图片预览

文档简介
沪科版七年级下册数学8.2整式乘法(2)
多项式与多项式相乘同步练习
一、选择题(本大题共8小题)
1. 已知a+b=2,ab=1,化简(a-2)(b-2)的结果为( )
A.1 B.2 C.-1 21世纪教育网版权所有
2. 方程(x-3)(x+4)=(x+5)(x-6)的解是( )
A.x=9 B.x=-9 C.x=6 D.x=-6
3.下列计算中,正确的有( )
①(2a-3)(3a-1)=6a2-11a+3;
②(m+n)(n+m)=m2+mn+n2;
③(a-2)(a+3)=a2-6;
④(1-a)(1+a)=1-a2.
A.4个 B.3个 C.2个 D.1个
4. 若(x+m)(x-5)的积中不含x的一次项,则m的值为( )
A.0 B.5 C.-5 D.5或-5
5. 若一个长方体的长、宽、高分别是3x-4,2x-1和x,则它的体积是( )
A.6x3-5x2+4x B.6x3-11x2+4x
C.6x3-4x2 D.6x3-4x2+x+4
6. 设M=(x-3)(x-7),N=(x-2)(x-8),则M与N的关系为( )
A.MN C.M=N D.不能确定
7.一个长方形的长2xcm,宽比长少4 cm,若将长和宽都增加3 cm,则面积增大了__________cm2,若x=3,则增加的面积为__________cm2.下列选项正确的是( )。21·cn·jy·com
A. 12x-3 ;33 B. 24x-3 ;24 C. 24x-3 ;33 D. 12x-3 ;24 21*cnjy*com
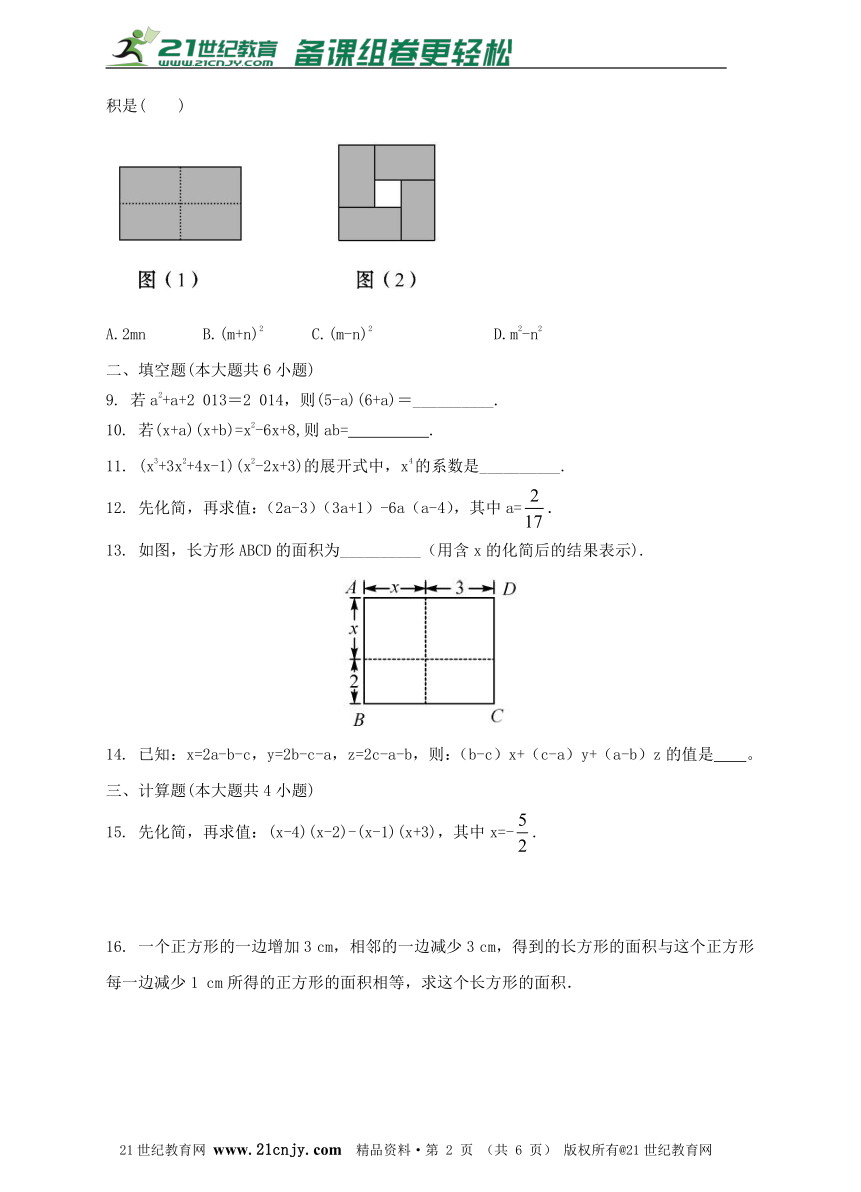
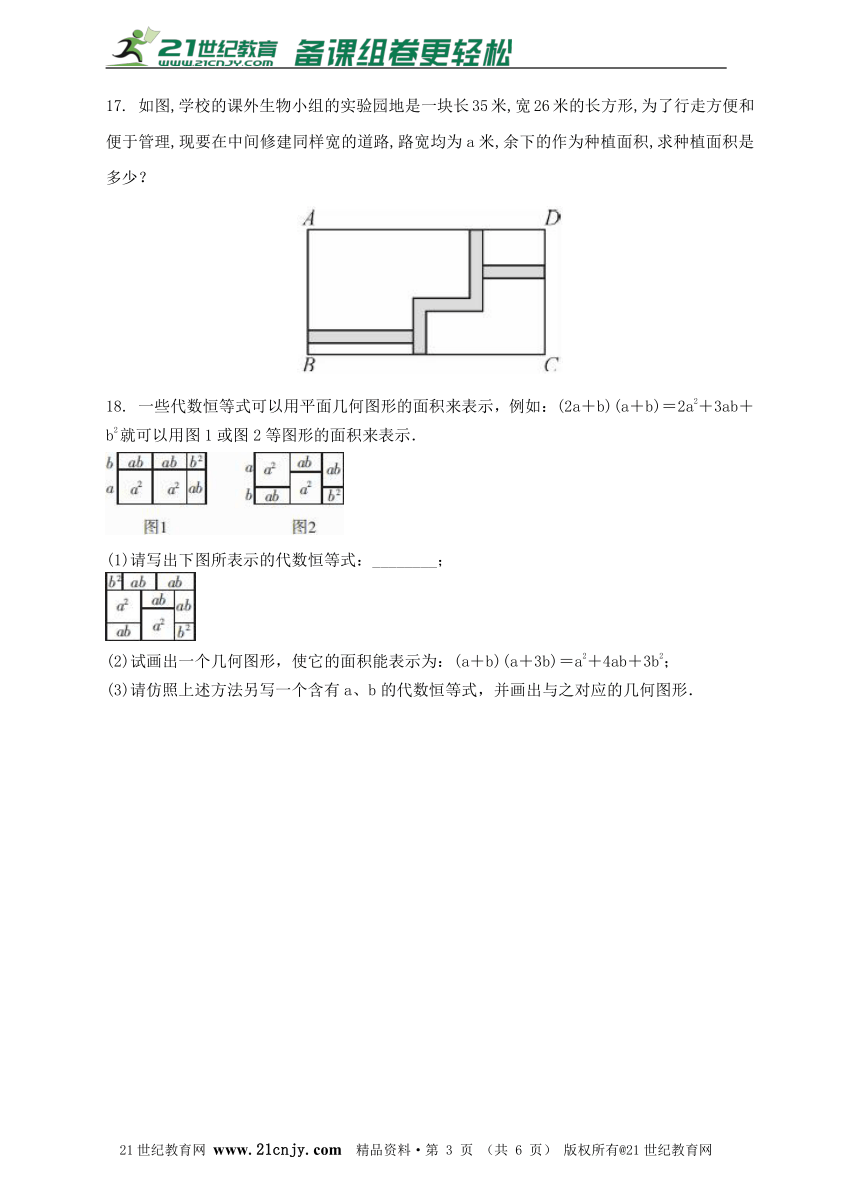
8. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )【出处:21教育名师】
A.2mn B.(m+n)2 C.(m-n)2 D.m2-n2
二、填空题(本大题共6小题)
9. 若a2+a+2 013=2 014,则(5-a)(6+a)=__________.
10. 若(x+a)(x+b)=x2-6x+8,则ab= .
11. (x3+3x2+4x-1)(x2-2x+3)的展开式中,x4的系数是__________.
12. 先化简,再求值:(2a-3)(3a+1)-6a(a-4),其中a=.
13. 如图,长方形ABCD的面积为__________(用含x的化简后的结果表示).
14. 已知:x=2a-b-c,y=2b-c-a,z=2c-a-b,则:(b-c)x+(c-a)y+(a-b)z的值是 。
三、计算题(本大题共4小题)
15. 先化简,再求值:(x-4)(x-2)-(x-1)(x+3),其中x=-.
一个正方形的一边增加3 cm,相邻的一边减少3 cm,得到的长方形的面积与这个正方形每一边减少1 cm所得的正方形的面积相等,求这个长方形的面积.2-1-c-n-j-y
17. 如图,学校的课外生物小组的实验园地是一块长35米,宽26米的长方形,为了行走方便和便于管理,现要在中间修建同样宽的道路,路宽均为a米,余下的作为种植面积,求种植面积是多少?21教育名师原创作品
18. 一些代数恒等式可以用平面几何图形的面积来表示,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2等图形的面积来表示.【版权所有:21教育】
(1)请写出下图所表示的代数恒等式:________;
(2)试画出一个几何图形,使它的面积能表示为:(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述方法另写一个含有a、b的代数恒等式,并画出与之对应的几何图形.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:根据多项式乘多项式的运算法则进行计算,根据系数关系解答。
解:(a-2)(b-2)
=ab-2(a+b)+4,
当a+b= ,ab=1时,原式=1-2×+4=2.故选B。
2.B
分析:利用多项式乘积,化简即可求得。
解:根据(x-3)(x+4)=x2+x-12,(x+5)(x-6))=x2-x-30,解答得到x=-9,选B
3.C
分析:根据平方差公式、完全平方公式以及多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.www.21-cn-jy.com
解:.因为(2a-3)(3a-1)=6a2-11a+3;
(m+n)(n+m)=m2+2mn+n2;(a-2)(a+3)=a2+a-6;(1-a)(1+a)=1-a2,故正确的有2个. 选C
4. B
分析:把式子展开,找到x的一次项的所有系数,令其为0,可求出m的值.
解:∵(x+m)(x-5)=x2+(m-5)x-5m,
又∵结果中不含x的一次项,
∴m-5=0,
解得m=5.故选B
5. B
分析:结合多项式的乘法运算解答即可。
解:根据题意得:x(3x-4)(2x-1)=x(6x2-11x+4)=6x3-11x2+4x. 故选B.21cnjy.com
6. B
分析:根据多项式乘多项式的运算法则进行计算,比较即可得到答案。
解:M=(x-3)(x-7)=x2-10x+21, N=(x-2)(x-8)= x2-10x+16,M-N=5,故M>N,选B。
7.A
分析:面积增大了 (2x+3)(2x-4+3)-2x(2x-4) =(2x+3)(2x-1)-4x2+8x =4x2-2x+6x-3-4x2+8x =12x-3 若x=3cm,则增大的面积为12x-3=12×3-3=36-3=33cm221·世纪*教育网
解:答案为 12x-3 ;33 故选A。
8. C
解:由题意可得,正方形的边长为(m+n),故正方形的面积为(m+n)2,又因为原矩形的面积为4mn,所以中间空的部分的面积=(m+n)2-4mn=(m-n)2. 选C.【来源:21·世纪·教育·网】
二、填空题(本大题共6小题)
9. 分析:本题需先把代数式进行化简,最后把相关代数式代入即可求出正确答案.
解:a2+a+2 013=2 014,所以a2+a=1
又因为(5-a)(6+a)=-a2-a+30,则(5-a)(6+a)=-1+30=29.
10.分析:利用多项式乘法法则计算列出二元二次方程解答可得。
解:因为(x+a)(x+b)=x2+bx+ax+ab=x2+(a+b)x+ab,所以x2+(a+b)x+ab=【来源:21cnj*y.co*m】
x2-6x+8,所以ab=8.答案:8
11.分析:利用多项式乘法法则计算解答可得。
解:(x3+3x2+4x-1)(x2-2x+3)= x5+x4-3x3+8 x2+14x-3,x4的系数是1.21*cnjy*com
12.分析:在求代数式的值时,应先化简后代值计算,使运算简便.
解:(2a-3)(3a+1)-6a(a-4)
=6a2+2a-9a-3-6a2+24a
=17a-3
当a=时,原式=17×-3=-1.
13.分析:多项式乘多项式运算法则解答即可。
解: 根据题意得:(x+3)(x+2)=x2+5x+6,
14.解:(x-1)(x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
…
规律为左边都有(x-1)和关于x的多项式,常数项和每项系数均为1;
右边多项式的次数比左边多项式的次数大1.
故(x-1)(xn-1+xn-2+xn-3+…+x+1)=xn-1.故答案为:xn-1.
三、计算题(本大题共3小题)
15.分析:利用多项式乘法法则计算
解:(x-4)(x-2)-(x-1)(x+3)=x2-6x+8-(x2+2x-3)=-8x+11.
把x=-代入原式,得原式=-8x+11=-8×(-)+11=31.
16. 分析:设原来正方形的边长为xcm,长方形长为x+3,宽为x-3,根据面积相等列出关系式,解得x,进而得到原来正方形的面积.21教育网
解:设正方形的边长为x cm.依题意得(x+3)(x-3)=(x-1)(x-1).解得x=5.∴长方形的面积为(5+3)×(5-3)=16(cm2).2·1·c·n·j·y
17. 分析:利用平移将横向的道路都平移到BC上,纵向的道路都平移到CD上,则不难发现剩余部分恰好是一个长为(35-a)米,宽为(26-a)米的长方形,www-2-1-cnjy-com
解:种植面积为:(35-a)(26-a)=910-61a+a2(平方米).
18.分析:对几何图形作出代数解释和用几何图形的面积表示代数恒等式是互逆的,一般是从面积方面进行考虑.本题需用拼图的方法和同一图形面积的不同表示来解题.
解: (1)(2a+b)(a+2b)=2a2+5ab+2b2;
(2)答案不唯一,如图所示;
(3)答案不唯一,如a(a+2b)=a2+2ab,与之对应的几何图形如图.
多项式与多项式相乘同步练习
一、选择题(本大题共8小题)
1. 已知a+b=2,ab=1,化简(a-2)(b-2)的结果为( )
A.1 B.2 C.-1 21世纪教育网版权所有
2. 方程(x-3)(x+4)=(x+5)(x-6)的解是( )
A.x=9 B.x=-9 C.x=6 D.x=-6
3.下列计算中,正确的有( )
①(2a-3)(3a-1)=6a2-11a+3;
②(m+n)(n+m)=m2+mn+n2;
③(a-2)(a+3)=a2-6;
④(1-a)(1+a)=1-a2.
A.4个 B.3个 C.2个 D.1个
4. 若(x+m)(x-5)的积中不含x的一次项,则m的值为( )
A.0 B.5 C.-5 D.5或-5
5. 若一个长方体的长、宽、高分别是3x-4,2x-1和x,则它的体积是( )
A.6x3-5x2+4x B.6x3-11x2+4x
C.6x3-4x2 D.6x3-4x2+x+4
6. 设M=(x-3)(x-7),N=(x-2)(x-8),则M与N的关系为( )
A.M
7.一个长方形的长2xcm,宽比长少4 cm,若将长和宽都增加3 cm,则面积增大了__________cm2,若x=3,则增加的面积为__________cm2.下列选项正确的是( )。21·cn·jy·com
A. 12x-3 ;33 B. 24x-3 ;24 C. 24x-3 ;33 D. 12x-3 ;24 21*cnjy*com
8. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )【出处:21教育名师】
A.2mn B.(m+n)2 C.(m-n)2 D.m2-n2
二、填空题(本大题共6小题)
9. 若a2+a+2 013=2 014,则(5-a)(6+a)=__________.
10. 若(x+a)(x+b)=x2-6x+8,则ab= .
11. (x3+3x2+4x-1)(x2-2x+3)的展开式中,x4的系数是__________.
12. 先化简,再求值:(2a-3)(3a+1)-6a(a-4),其中a=.
13. 如图,长方形ABCD的面积为__________(用含x的化简后的结果表示).
14. 已知:x=2a-b-c,y=2b-c-a,z=2c-a-b,则:(b-c)x+(c-a)y+(a-b)z的值是 。
三、计算题(本大题共4小题)
15. 先化简,再求值:(x-4)(x-2)-(x-1)(x+3),其中x=-.
一个正方形的一边增加3 cm,相邻的一边减少3 cm,得到的长方形的面积与这个正方形每一边减少1 cm所得的正方形的面积相等,求这个长方形的面积.2-1-c-n-j-y
17. 如图,学校的课外生物小组的实验园地是一块长35米,宽26米的长方形,为了行走方便和便于管理,现要在中间修建同样宽的道路,路宽均为a米,余下的作为种植面积,求种植面积是多少?21教育名师原创作品
18. 一些代数恒等式可以用平面几何图形的面积来表示,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2等图形的面积来表示.【版权所有:21教育】
(1)请写出下图所表示的代数恒等式:________;
(2)试画出一个几何图形,使它的面积能表示为:(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述方法另写一个含有a、b的代数恒等式,并画出与之对应的几何图形.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:根据多项式乘多项式的运算法则进行计算,根据系数关系解答。
解:(a-2)(b-2)
=ab-2(a+b)+4,
当a+b= ,ab=1时,原式=1-2×+4=2.故选B。
2.B
分析:利用多项式乘积,化简即可求得。
解:根据(x-3)(x+4)=x2+x-12,(x+5)(x-6))=x2-x-30,解答得到x=-9,选B
3.C
分析:根据平方差公式、完全平方公式以及多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.www.21-cn-jy.com
解:.因为(2a-3)(3a-1)=6a2-11a+3;
(m+n)(n+m)=m2+2mn+n2;(a-2)(a+3)=a2+a-6;(1-a)(1+a)=1-a2,故正确的有2个. 选C
4. B
分析:把式子展开,找到x的一次项的所有系数,令其为0,可求出m的值.
解:∵(x+m)(x-5)=x2+(m-5)x-5m,
又∵结果中不含x的一次项,
∴m-5=0,
解得m=5.故选B
5. B
分析:结合多项式的乘法运算解答即可。
解:根据题意得:x(3x-4)(2x-1)=x(6x2-11x+4)=6x3-11x2+4x. 故选B.21cnjy.com
6. B
分析:根据多项式乘多项式的运算法则进行计算,比较即可得到答案。
解:M=(x-3)(x-7)=x2-10x+21, N=(x-2)(x-8)= x2-10x+16,M-N=5,故M>N,选B。
7.A
分析:面积增大了 (2x+3)(2x-4+3)-2x(2x-4) =(2x+3)(2x-1)-4x2+8x =4x2-2x+6x-3-4x2+8x =12x-3 若x=3cm,则增大的面积为12x-3=12×3-3=36-3=33cm221·世纪*教育网
解:答案为 12x-3 ;33 故选A。
8. C
解:由题意可得,正方形的边长为(m+n),故正方形的面积为(m+n)2,又因为原矩形的面积为4mn,所以中间空的部分的面积=(m+n)2-4mn=(m-n)2. 选C.【来源:21·世纪·教育·网】
二、填空题(本大题共6小题)
9. 分析:本题需先把代数式进行化简,最后把相关代数式代入即可求出正确答案.
解:a2+a+2 013=2 014,所以a2+a=1
又因为(5-a)(6+a)=-a2-a+30,则(5-a)(6+a)=-1+30=29.
10.分析:利用多项式乘法法则计算列出二元二次方程解答可得。
解:因为(x+a)(x+b)=x2+bx+ax+ab=x2+(a+b)x+ab,所以x2+(a+b)x+ab=【来源:21cnj*y.co*m】
x2-6x+8,所以ab=8.答案:8
11.分析:利用多项式乘法法则计算解答可得。
解:(x3+3x2+4x-1)(x2-2x+3)= x5+x4-3x3+8 x2+14x-3,x4的系数是1.21*cnjy*com
12.分析:在求代数式的值时,应先化简后代值计算,使运算简便.
解:(2a-3)(3a+1)-6a(a-4)
=6a2+2a-9a-3-6a2+24a
=17a-3
当a=时,原式=17×-3=-1.
13.分析:多项式乘多项式运算法则解答即可。
解: 根据题意得:(x+3)(x+2)=x2+5x+6,
14.解:(x-1)(x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
…
规律为左边都有(x-1)和关于x的多项式,常数项和每项系数均为1;
右边多项式的次数比左边多项式的次数大1.
故(x-1)(xn-1+xn-2+xn-3+…+x+1)=xn-1.故答案为:xn-1.
三、计算题(本大题共3小题)
15.分析:利用多项式乘法法则计算
解:(x-4)(x-2)-(x-1)(x+3)=x2-6x+8-(x2+2x-3)=-8x+11.
把x=-代入原式,得原式=-8x+11=-8×(-)+11=31.
16. 分析:设原来正方形的边长为xcm,长方形长为x+3,宽为x-3,根据面积相等列出关系式,解得x,进而得到原来正方形的面积.21教育网
解:设正方形的边长为x cm.依题意得(x+3)(x-3)=(x-1)(x-1).解得x=5.∴长方形的面积为(5+3)×(5-3)=16(cm2).2·1·c·n·j·y
17. 分析:利用平移将横向的道路都平移到BC上,纵向的道路都平移到CD上,则不难发现剩余部分恰好是一个长为(35-a)米,宽为(26-a)米的长方形,www-2-1-cnjy-com
解:种植面积为:(35-a)(26-a)=910-61a+a2(平方米).
18.分析:对几何图形作出代数解释和用几何图形的面积表示代数恒等式是互逆的,一般是从面积方面进行考虑.本题需用拼图的方法和同一图形面积的不同表示来解题.
解: (1)(2a+b)(a+2b)=2a2+5ab+2b2;
(2)答案不唯一,如图所示;
(3)答案不唯一,如a(a+2b)=a2+2ab,与之对应的几何图形如图.
