8.3完全平方公式与平方差同步练习
图片预览


文档简介
沪科版七年级下册数学8.3.2完全平方公式同步练习
一、选择题(本大题共8小题)
1. 若x=1,,则x2+4xy+4y2的值是( )
A.2 B.4 C. D.
2.下面各运算中,结果正确的是( )
A.2a3+3a3=5a6
B.-a2 a3=a5
C.(a+b)(-a-b)=a2-b2
D.(-a-b)2=a2+2ab+b2
3. 若(ax+3y)2=4x2+12xy+by2,则a,b的值分别为( )
A.a=4,b=3 B.a=2,b=3
C.a=4,b=9 D.a=2,b=9
4. 若a+=7,则a2+的值为( )
A.47 B.9 C.5 D.51
5. 已知多项式x2+kx+是一个完全平方式,则k的值为( )
A.±1 B.﹣1 C.1 D.
6.已知(a+b)2-2ab=5,则a2+b2的值为( )
A.10 B.5 C.1 D.不能确定
7. 如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )21教育网
A.a2+4 B.2a2+4 C.3a2-4a-4 D.4a2-a-2
8.下列运算中,正确的运算有( )
①(x+2y)2=x2+4y2;②(a-2b)2=a2-4ab+4b2;③(x+y)2=x2-2xy+y2;④(x-)2=x2-x+.21cnjy.com
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题)
9.已知:a-b=3,ab=1,则a2-3ab+b2=_____.
10. 若4x2﹣2kx+1是完全平方式,则k= .
11. 若a2+b2=7,ab=2,则(a-b)2的结果是________.
12. 已知实数a、b满足(a+b)2=1和(a-b)2=25,则a2+b2+ab= .
13.若a2b2+a2+b2+1-2ab=2ab,则a+b的值为_____.
14. 观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,7×9=82-1,……,请你把发现的规律用含字母n(n为正整数)的等式表示为_________________________.
三、计算题(本大题共4小题)
15.计算:(3x﹣2)(2x+3)﹣(x﹣1)2;
16.已知(a+b)2=24,(a-b)2=20,求:
(1)ab的值是多少?
(2)a2+b2的值是多少?
17. 先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
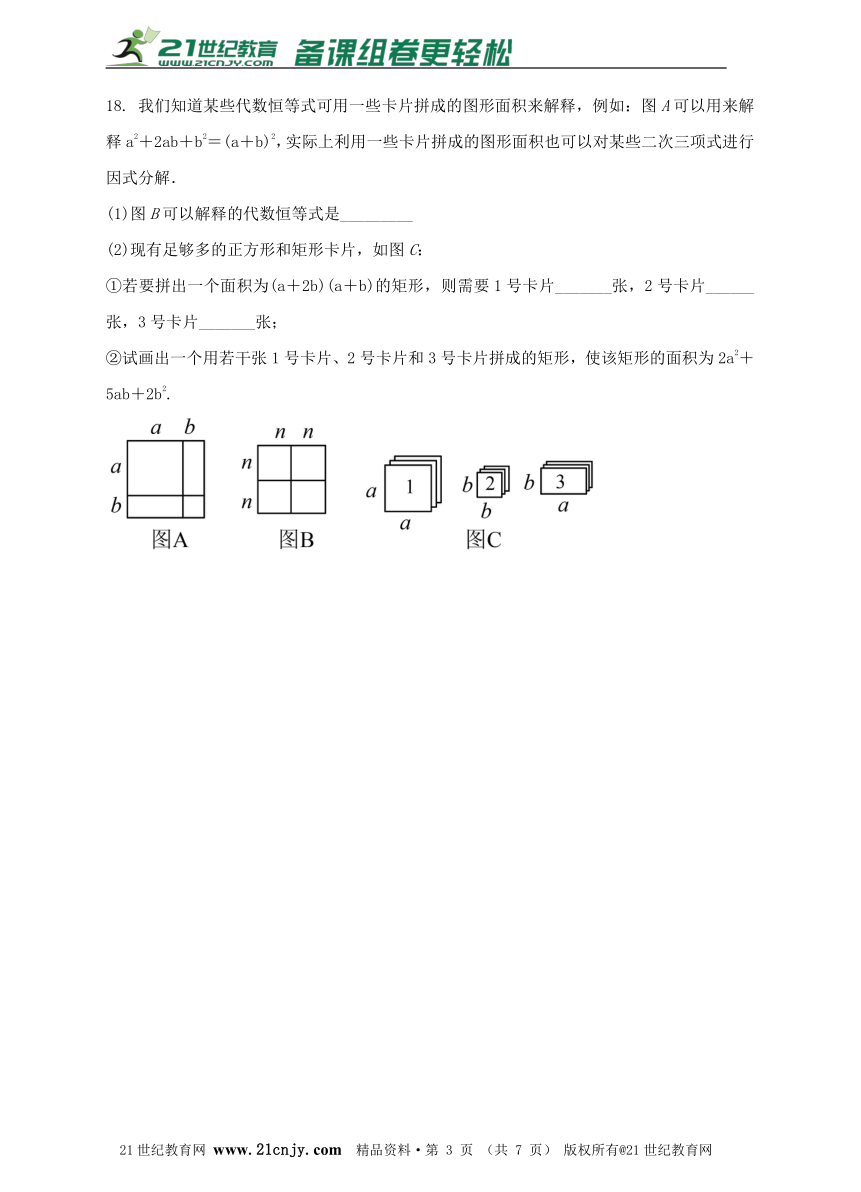
18. 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释a2+2ab+b2=(a+b)2,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.2·1·c·n·j·y
(1)图B可以解释的代数恒等式是_________
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为(a+2b)(a+b)的矩形,则需要1号卡片_______张,2号卡片______张,3号卡片_______张;【来源:21·世纪·教育·网】
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为2a2+5ab+2b2.【来源:21cnj*y.co*m】
参考答案:
一、选择题(本大题共8小题)
1.B
分析:首先用完全平方公式将原式化简,然后再代值计算.
解:原式=(x+2y)2=(1+2×)2=4.故选B.
2.D
分析:A、原式合并同类项得到结果,即可做出判断;
B、原式利用同底数幂的乘法法则计算得到结果,即可做出判断;
C、原式变形后,利用完全平方公式展开得到结果,即可做出判断;
D、原式利用完全平方公式展开得到结果,即可做出判断.
解:A、原式=5a3,故选项错误;
B、原式=-a5,故选项错误;
C、原式=-(a+b)2=-a2-2ab-b2,故选项错误;21·cn·jy·com
D、原式=(a+b)2=a2+2ab+b2,故选项正确.故选D.
3.D
分析:利用完全平方公式进行展开并合并同类型后借助系数解答即可。
解; (ax+3y)2=a2x2+6axy+9y2=4x2+12xy+by2
故得到:a=2,b=9,故选D。
4.A
分析:利用完全公式转化可解答;
解:(a+)2 =49=a2++2,则a2+=47,故选A
5. A
分析:这里首末两项是x和这两个数的平方,那么中间一项为加上或减去x和积的2倍.
解:∵多项式x2+kx+是一个完全平方式,
∴x2+kx+=(x±)2,
∴k=±1,
故选A.
6.B
分析:根据完全平方公式把(a+b)2展开,整理即可.
解::∵(a+b)2-2ab=5,
∴a2+2ab+b2-2ab=5,
∴a2+b2的值为5.故选B.
7. C
分析:根据拼成的平行四边形的面积等于大正方形的面积减去小正方形的面积,列式整理即可得解.
解:(2a)2﹣(a+2)2
=4a2﹣a2﹣4a﹣4
=3a2﹣4a﹣4,
故选:C.
8.B
分析:结合完全平方公式进行运算后进行核对即可。
解:(1)(x+2y)2=x2+4xy+4y2 故错误;(2) (a-2b)2=a2-4ab+4b2正确(3)(x+y)2=x2+2xy+y2故错误;(4)(x-)2=x2-x+.正确。故选B.www.21-cn-jy.com
二、填空题(本大题共6小题)
9.分析:应把所给式子整理为含(a-b)2和ab的式子,然后把值代入即可.
解:∵(a-b)2=32=9,
∴a2-3ab+b2=(a-b)2-ab=9-1=8
10. 分析:这里首末两项是2x和1这两个数的平方,那么中间一项为加上或减去2x和1积的2倍.
解:∵4x2﹣2kx+1是完全平方式,
∵4x2±4x+1=(2x±1)2是完全平方式,
∴﹣2k=±4,
解得k=±2.
11. 分析:根据已知直接将原式展开,利用a2+b2=7,ab=2,直接代入即可.
解:∵a2+b2=7,ab=2,
∴(a-b)2=a2+b2-2ab=7-4=3.
故答案为:3.
12. 分析:首先由(a+b)2=1和(a-b)2=25,可求得a2+b2+2ab=1,a2+b2-2ab=25,然后将a2+b2与ab看作整体,解方程即可求得其值,则可求得答案.www-2-1-cnjy-com
解:∵(a+b)2=1,(a-b)2=25,
∴a2+b2+2ab=1①,a2+b2-2ab=25②,
+②得:a2+b2=13,①-②得:ab=-6,∴a2+b2+ab=13-6=7.
故答案为:7.
13.分析:首先把2ab移到等式的左边,然后变为a2b2+a2+b2+1-2ab-2ab=0,接着利用完全平方公式分解因式,最后利用非负数的性质即可求解.2-1-c-n-j-y
解:∵a2b2+a2+b2+1-2ab=2ab,
∴a2b2+a2+b2+1-2ab-2ab=0,
∴a2b2-2ab+1+a2+b2-2ab=0,
∴(ab-1)2+(a-b)2=0,
∴ab=1,a-b=0,
∴a=b=1或-1,
∴a+b=2或-2.
14.解:根据题意可得:
规律为(2n-1)(2n+1)=(2n)2-1,
故答案为(2n-1)(2n+1)=(2n)2-1.
三、计算题(本大题共4小题)
15. 分析:原式第一项利用多项式乘多项式法则计算,第二项利用完全平方公式展开,去括号合并即可得到结果;21世纪教育网版权所有
解:(1)原式=6x2+9x﹣4x﹣6﹣x2+2x﹣1=5x2+7x﹣7;
16.分析:由(a+b)2=24,(a-b)2=20,可以得到:a2+b2+2ab=24…①,a2+b2-2ab=20…②,通过两式的加减即可求解.21*cnjy*com
解:∵(a+b)2=24,(a-b)2=20,
∴a2+b2+2ab=24…①,
a2+b2-2ab=20…②,
(1)①-②得:4ab=4,则ab=1;
(2)①+②得:2(a2+b2)=44,则a2+b2=22.
17. 分析:原式中括号中第一项利用完全平方公式展开,第二项利用单项式乘以多项式法则计算,合并后利用多项式除以单项式法则计算得到最简结果,将x与y的值代入计算即可求出值.【出处:21教育名师】
解:原式=(x2﹣4xy+4y2﹣x2+4xy﹣8xy)÷4y=(4y2﹣12xy)÷4y=y﹣3x,
当x=﹣1,y=2时,原式=2+3=5.
18. 分析:(1)根据图所示,可以得到正方形面积为,即四个小正方形面积之和,即
(2)①根据题意,可以画出相应的图形,如图所示
21·世纪*教育网
由此可知1号卡片1张,2号卡片2张,3好卡片3张
②根据题意,可以画出相关的图形
解; (1) (2)①.1,2,3
②.
=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 4 页 (共 7 页) 版权所有@21世纪教育网
一、选择题(本大题共8小题)
1. 若x=1,,则x2+4xy+4y2的值是( )
A.2 B.4 C. D.
2.下面各运算中,结果正确的是( )
A.2a3+3a3=5a6
B.-a2 a3=a5
C.(a+b)(-a-b)=a2-b2
D.(-a-b)2=a2+2ab+b2
3. 若(ax+3y)2=4x2+12xy+by2,则a,b的值分别为( )
A.a=4,b=3 B.a=2,b=3
C.a=4,b=9 D.a=2,b=9
4. 若a+=7,则a2+的值为( )
A.47 B.9 C.5 D.51
5. 已知多项式x2+kx+是一个完全平方式,则k的值为( )
A.±1 B.﹣1 C.1 D.
6.已知(a+b)2-2ab=5,则a2+b2的值为( )
A.10 B.5 C.1 D.不能确定
7. 如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )21教育网
A.a2+4 B.2a2+4 C.3a2-4a-4 D.4a2-a-2
8.下列运算中,正确的运算有( )
①(x+2y)2=x2+4y2;②(a-2b)2=a2-4ab+4b2;③(x+y)2=x2-2xy+y2;④(x-)2=x2-x+.21cnjy.com
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题)
9.已知:a-b=3,ab=1,则a2-3ab+b2=_____.
10. 若4x2﹣2kx+1是完全平方式,则k= .
11. 若a2+b2=7,ab=2,则(a-b)2的结果是________.
12. 已知实数a、b满足(a+b)2=1和(a-b)2=25,则a2+b2+ab= .
13.若a2b2+a2+b2+1-2ab=2ab,则a+b的值为_____.
14. 观察下列各式:1×3=22-1,3×5=42-1,5×7=62-1,7×9=82-1,……,请你把发现的规律用含字母n(n为正整数)的等式表示为_________________________.
三、计算题(本大题共4小题)
15.计算:(3x﹣2)(2x+3)﹣(x﹣1)2;
16.已知(a+b)2=24,(a-b)2=20,求:
(1)ab的值是多少?
(2)a2+b2的值是多少?
17. 先化简,再求值:[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y,其中x=﹣1,y=2.
18. 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释a2+2ab+b2=(a+b)2,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.2·1·c·n·j·y
(1)图B可以解释的代数恒等式是_________
(2)现有足够多的正方形和矩形卡片,如图C:
①若要拼出一个面积为(a+2b)(a+b)的矩形,则需要1号卡片_______张,2号卡片______张,3号卡片_______张;【来源:21·世纪·教育·网】
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为2a2+5ab+2b2.【来源:21cnj*y.co*m】
参考答案:
一、选择题(本大题共8小题)
1.B
分析:首先用完全平方公式将原式化简,然后再代值计算.
解:原式=(x+2y)2=(1+2×)2=4.故选B.
2.D
分析:A、原式合并同类项得到结果,即可做出判断;
B、原式利用同底数幂的乘法法则计算得到结果,即可做出判断;
C、原式变形后,利用完全平方公式展开得到结果,即可做出判断;
D、原式利用完全平方公式展开得到结果,即可做出判断.
解:A、原式=5a3,故选项错误;
B、原式=-a5,故选项错误;
C、原式=-(a+b)2=-a2-2ab-b2,故选项错误;21·cn·jy·com
D、原式=(a+b)2=a2+2ab+b2,故选项正确.故选D.
3.D
分析:利用完全平方公式进行展开并合并同类型后借助系数解答即可。
解; (ax+3y)2=a2x2+6axy+9y2=4x2+12xy+by2
故得到:a=2,b=9,故选D。
4.A
分析:利用完全公式转化可解答;
解:(a+)2 =49=a2++2,则a2+=47,故选A
5. A
分析:这里首末两项是x和这两个数的平方,那么中间一项为加上或减去x和积的2倍.
解:∵多项式x2+kx+是一个完全平方式,
∴x2+kx+=(x±)2,
∴k=±1,
故选A.
6.B
分析:根据完全平方公式把(a+b)2展开,整理即可.
解::∵(a+b)2-2ab=5,
∴a2+2ab+b2-2ab=5,
∴a2+b2的值为5.故选B.
7. C
分析:根据拼成的平行四边形的面积等于大正方形的面积减去小正方形的面积,列式整理即可得解.
解:(2a)2﹣(a+2)2
=4a2﹣a2﹣4a﹣4
=3a2﹣4a﹣4,
故选:C.
8.B
分析:结合完全平方公式进行运算后进行核对即可。
解:(1)(x+2y)2=x2+4xy+4y2 故错误;(2) (a-2b)2=a2-4ab+4b2正确(3)(x+y)2=x2+2xy+y2故错误;(4)(x-)2=x2-x+.正确。故选B.www.21-cn-jy.com
二、填空题(本大题共6小题)
9.分析:应把所给式子整理为含(a-b)2和ab的式子,然后把值代入即可.
解:∵(a-b)2=32=9,
∴a2-3ab+b2=(a-b)2-ab=9-1=8
10. 分析:这里首末两项是2x和1这两个数的平方,那么中间一项为加上或减去2x和1积的2倍.
解:∵4x2﹣2kx+1是完全平方式,
∵4x2±4x+1=(2x±1)2是完全平方式,
∴﹣2k=±4,
解得k=±2.
11. 分析:根据已知直接将原式展开,利用a2+b2=7,ab=2,直接代入即可.
解:∵a2+b2=7,ab=2,
∴(a-b)2=a2+b2-2ab=7-4=3.
故答案为:3.
12. 分析:首先由(a+b)2=1和(a-b)2=25,可求得a2+b2+2ab=1,a2+b2-2ab=25,然后将a2+b2与ab看作整体,解方程即可求得其值,则可求得答案.www-2-1-cnjy-com
解:∵(a+b)2=1,(a-b)2=25,
∴a2+b2+2ab=1①,a2+b2-2ab=25②,
+②得:a2+b2=13,①-②得:ab=-6,∴a2+b2+ab=13-6=7.
故答案为:7.
13.分析:首先把2ab移到等式的左边,然后变为a2b2+a2+b2+1-2ab-2ab=0,接着利用完全平方公式分解因式,最后利用非负数的性质即可求解.2-1-c-n-j-y
解:∵a2b2+a2+b2+1-2ab=2ab,
∴a2b2+a2+b2+1-2ab-2ab=0,
∴a2b2-2ab+1+a2+b2-2ab=0,
∴(ab-1)2+(a-b)2=0,
∴ab=1,a-b=0,
∴a=b=1或-1,
∴a+b=2或-2.
14.解:根据题意可得:
规律为(2n-1)(2n+1)=(2n)2-1,
故答案为(2n-1)(2n+1)=(2n)2-1.
三、计算题(本大题共4小题)
15. 分析:原式第一项利用多项式乘多项式法则计算,第二项利用完全平方公式展开,去括号合并即可得到结果;21世纪教育网版权所有
解:(1)原式=6x2+9x﹣4x﹣6﹣x2+2x﹣1=5x2+7x﹣7;
16.分析:由(a+b)2=24,(a-b)2=20,可以得到:a2+b2+2ab=24…①,a2+b2-2ab=20…②,通过两式的加减即可求解.21*cnjy*com
解:∵(a+b)2=24,(a-b)2=20,
∴a2+b2+2ab=24…①,
a2+b2-2ab=20…②,
(1)①-②得:4ab=4,则ab=1;
(2)①+②得:2(a2+b2)=44,则a2+b2=22.
17. 分析:原式中括号中第一项利用完全平方公式展开,第二项利用单项式乘以多项式法则计算,合并后利用多项式除以单项式法则计算得到最简结果,将x与y的值代入计算即可求出值.【出处:21教育名师】
解:原式=(x2﹣4xy+4y2﹣x2+4xy﹣8xy)÷4y=(4y2﹣12xy)÷4y=y﹣3x,
当x=﹣1,y=2时,原式=2+3=5.
18. 分析:(1)根据图所示,可以得到正方形面积为,即四个小正方形面积之和,即
(2)①根据题意,可以画出相应的图形,如图所示
21·世纪*教育网
由此可知1号卡片1张,2号卡片2张,3好卡片3张
②根据题意,可以画出相关的图形
解; (1) (2)①.1,2,3
②.
=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 4 页 (共 7 页) 版权所有@21世纪教育网
