8.4因式分解同步练习
图片预览



文档简介
沪科版七年级下册数学8.4因式分解同步练习
一、选择题(本大题共8小题)
1. 下列各式从左到右的变形中,是因式分解的为( )
A.x(a﹣b)=ax﹣bx B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.x2﹣1=(x+1)(x﹣1) D.ax+bx+c=x(a+b)+c
2. 下列各式中,不含因式a+1的是( )
A.2a2+2a B.a2+2a+1 C.a2﹣1 D.
3. 若多项式x4+mx3+nx-16含有因式(x-2)和(x-1),则mn的值是( )
A.100 B.0 C.-100 D.502·1·c·n·j·y
4. 下列各式的变形中,正确的是( )
A. B.
C. D.
5. 多项式①2x2﹣x,②(x﹣1)2﹣4(x﹣1)+4,③(x+1)2﹣4x(x+1)+4,④﹣4x2﹣1+4x;分解因式后,结果含有相同因式的是( )【来源:21·世纪·教育·网】
A.①④ B.①② C.③④ D.②③
6. 已知不论x为何值,x2-kx-15=(x+5)(x-3),则k值为( )
A、2 B、-2 C、5 D、-3
7. 把多项式(m+1)(m-1)+(m-1)分解因式,一个因式是(m-1),则另一个因式是( )
A、m+1 B、2m C、2 D、m+2
8. 在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3﹣xy2,取x=20,y=10,用上述方法产生的密码不可能是( )21世纪教育网版权所有
A.201010 B.203010 C.301020 D.201030
二、填空题(本大题共6小题)
9. 简便计算:7.292﹣2.712= .
10. 如图所示,根据图形把多项式a2+5ab+4b2因式分解= .
11. 已知a2﹣a﹣1=0,则a3﹣a2﹣a+2016= .
12. 若对x恒成立,则n= .
13. 在实数范围内因式分解:= .
14. 已知a2﹣6a+9与|b﹣1|互为相反数,计算a3b3+2a2b2+ab的结果是 .
三、计算题(本大题共4小题)
15. 分解因式:
(1)2a(y﹣z)﹣3b(z﹣y)
(2)﹣a4+16
(3)a2b﹣2ab+b
(4)3(x﹣2y)2﹣3x+6y.
16. 下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A、提取公因式B.平方差公式
C、两数和的完全平方公式D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底 .(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果 .
请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
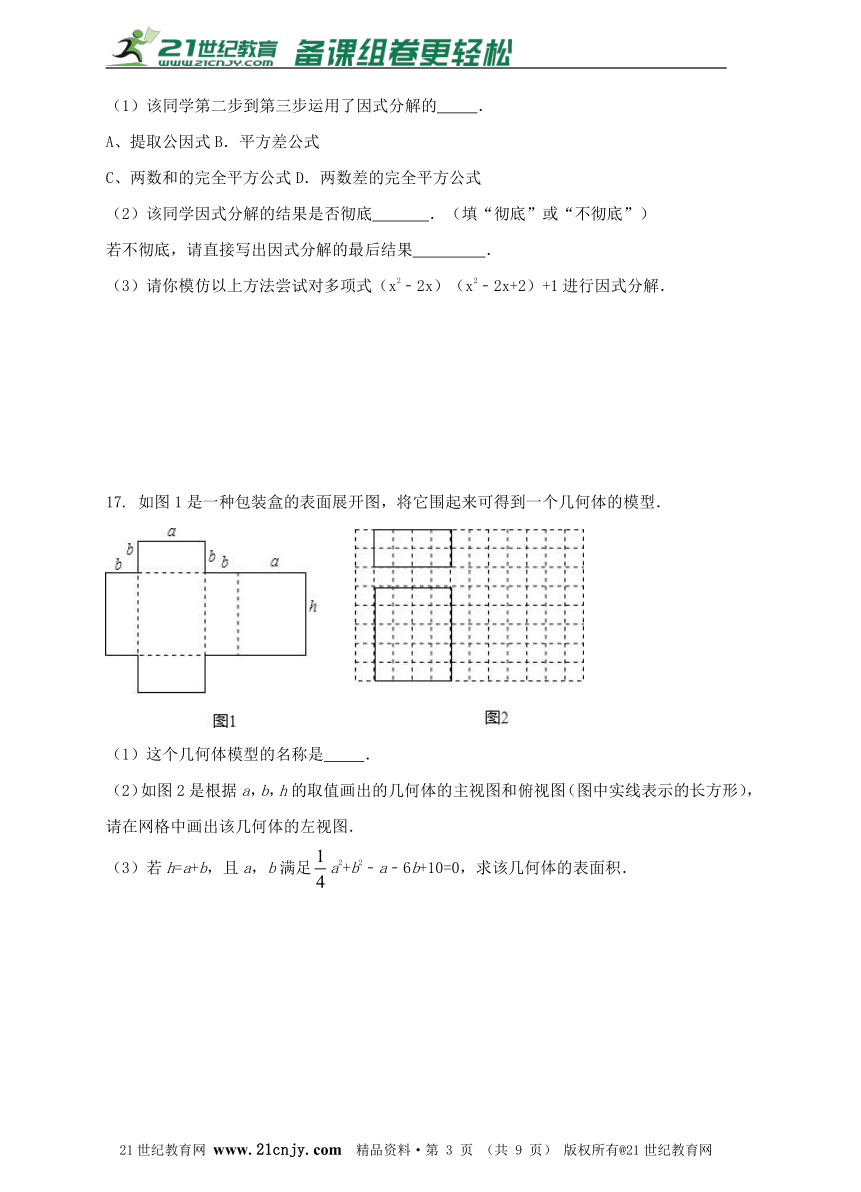
17. 如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.21教育网
若h=a+b,且a,b满足a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
18. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是怎样的?写出得到公式的过程.21·cn·jy·com
参考答案:
一、选择题(本大题共8小题)
1. C
分析:根据因式分解的定义作答.把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式.21·世纪*教育网
解:A、是整式的乘法运算,故选项错误;
B、结果不是积的形式,故选项错误;
C、x2﹣1=(x+1)(x﹣1),正确;
D、结果不是积的形式,故选项错误.
故选:C.
2. D
分析;本题需先对每个式子进行因式分解,即可得出不含因式a+1的式子.
解:A、∵2a2+2a=2a(a+1),故本选项正确;
B、a2+2a+1=(a+1)2,故本选项正确;
C、a2﹣1=(a+1)(a﹣1),故本选项正确;
D、=(a+2,故本选项错误.
故选D.
3. C
分析:根据因式分解的意义解答即可.
解:设x4+mx3+nx-16=(x-1)(x-2)(x2+ax+b),则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b.www-2-1-cnjy-com
比较系数得:a-3=m,b-3a+2=0,2a-3b=n,2b=-16,解得:a=-2,b=-8,m=-5,n=20,所以mn=-5×20=-100.故选C.2-1-c-n-j-y
4.A
分析:1.平方差公式;2.整式的除法;3.因式分解-十字相乘法等;4.分式的加减法.
解:A.,正确;
B.,错误;
C.,错误;
D.,错误;故选A.
5.A
分析:根据提公因式法和完全平方公式把各选项的多项式分解因式,然后再找出结果中含有相同因式的即可.
解:①2x2﹣x=x(2x﹣1);
②(x﹣1)2﹣4(x﹣1)+4=(x﹣3)2;
③(x+1)2﹣4x(x+1)+4无法分解因式;
④﹣4x2﹣1+4x=﹣(4x2﹣4x+1)=﹣(2x﹣1)2.
所以分解因式后,结果中含有相同因式的是①和④.
故选:A.
6. B
分析:直接利用多项式乘以多项式得出等式右边多项式进而得出k的值.
解:∵x2-kx-15=(x+5)(x-3),
∴x2-kx-15=x2+2x-15,
∴-k=2,则k=-2.故选B.
7. D
分析:把多项式(m+1)(m-1)+(m-1)提取公因式(m-1)后,即可知答案.
解:(m+1)(m-1)+(m-1)=(m-1)(m+1+1)=(m-1)(m+2),故选D.
8. A
分析:对多项式利用提公因式法分解因式,利用平方差公式分解因式,然后把数值代入计算即可确定出密码.
解:x3﹣xy2=x(x2﹣y2)=x(x+y)(x﹣y),
当x=20,y=10时,x=20,x+y=30,x﹣y=10,
组成密码的数字应包括20,30,10,
所以组成的密码不可能是201010.
故选A.
二、填空题(本大题共6小题)
9.分析:根据平方差公式,a2﹣b2=(a+b)(a﹣b),即可解答出;
解:根据平方差公式得,
7.292﹣2.712=(7.29+2.71)(7.29﹣2.71),
=10×4.58,
=45.8;
故答案为:45.8.
10. 分析:根据图形和等积法可以对题目中的式子进行因式分解.
解:由图可知,
a2+5ab+4b2=(a+b)(a+4b),
故答案为:(a+b)(a+4b).
11.分析:在代数式a3﹣a2﹣a+2016中提取出a,再将a2﹣a﹣1=0代入其中即可得出结论.
解:∵a2﹣a﹣1=0,
∴a3﹣a2﹣a+2016=a(a2﹣a﹣1)+2016=0+2016=2016.
故答案为:2016.
12.分析:因式分解-十字相乘法等.
解:∵,∴,故,解得:n=4.故答案为:4.
13.分析:实数范围内分解因式.
解:原式==,故答案为:.
14.分析:根据互为相反数的性质和非负数的性质求得a,b的值,再进一步代入求解.
解:a2﹣6a+9=(a﹣3)2.依题意得
(a﹣3)2+|b﹣1|=0,则
a﹣3=0.b﹣1=0,
解得 a=3,b=1.
所以a3b3+2a2b2+ab=ab(a2b2+2ab+1)=ab(ab+1)2=3×16=48,
故答案为:48.
三、计算题(本大题共4小题)
15. 分析:(1)直接提公因式y﹣z即可;
(2)利用平方差分解后,再利用平方差进行二次分解即可;
(3)首先提公因式b,再利用完全平方公式进行分解即可;
(4)首先把后两项组合提公因式3,再提公因式3(x﹣2y)即可.
解:(1)原式=2a(y﹣z)+3b(y﹣z)=(y﹣z)(2a+3b);
(2)原式=(4﹣a2)(4+a2)=(2﹣a)(2+a)(4+a2);
(3)原式=b(a2﹣2a+1)=b(a﹣1)2;
(4)原式=3(x﹣2y)2﹣3(x﹣2y)=3(x﹣2y)(x﹣2y﹣1).
16. 分析:(1)完全平方式是两数的平方和与这两个数积的两倍的和或差;
(2)x2﹣4x+4还可以分解,所以是不彻底.
(3)按照例题的分解方法进行分解即可.
解:(1)运用了C,两数和的完全平方公式;
(2)x2﹣4x+4还可以分解,分解不彻底;
(3)设x2﹣2x=y.
(x2﹣2x)(x2﹣2x+2)+1,
=y(y+2)+1,
=y2+2y+1,
=(y+1)2,
=(x2﹣2x+1)2,
=(x﹣1)4.
17. 分析:(1)侧面四个长方形和上下两个底面也是长方形,所以折叠后能围成长方体.
(2)根据图1所标注的相关线段的长度画出其左视图;
(3)对a2+b2﹣a﹣6b+10=0进行因式分解,求得a、b的值,则易求h的值,然后由几何体的表面积计算公式进行解答.21cnjy.com
解:(1)根据该包装盒的表面展开图知,该几何体模型的名称为:长方体或底面为长方形的直棱柱.
故答案为:长方体或底面为长方形的直棱柱;
(2)如图所示:
;
(3)由题意得,(a﹣1)2+(b﹣3)2=0,
则a=2,b=3,
所以h=a+b=2+3=5.
所以表面积为:2(2×3+5×2+3×5)=62.
18. 分析:根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.www.21-cn-jy.com
解:(a﹣b)2=a2﹣2ab+b2.
∵大正方形的面积=(a﹣b)2,
还可以表示为a2﹣2ab+b2,
∴(a﹣b)2=a2﹣2ab+b2.
一、选择题(本大题共8小题)
1. 下列各式从左到右的变形中,是因式分解的为( )
A.x(a﹣b)=ax﹣bx B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.x2﹣1=(x+1)(x﹣1) D.ax+bx+c=x(a+b)+c
2. 下列各式中,不含因式a+1的是( )
A.2a2+2a B.a2+2a+1 C.a2﹣1 D.
3. 若多项式x4+mx3+nx-16含有因式(x-2)和(x-1),则mn的值是( )
A.100 B.0 C.-100 D.502·1·c·n·j·y
4. 下列各式的变形中,正确的是( )
A. B.
C. D.
5. 多项式①2x2﹣x,②(x﹣1)2﹣4(x﹣1)+4,③(x+1)2﹣4x(x+1)+4,④﹣4x2﹣1+4x;分解因式后,结果含有相同因式的是( )【来源:21·世纪·教育·网】
A.①④ B.①② C.③④ D.②③
6. 已知不论x为何值,x2-kx-15=(x+5)(x-3),则k值为( )
A、2 B、-2 C、5 D、-3
7. 把多项式(m+1)(m-1)+(m-1)分解因式,一个因式是(m-1),则另一个因式是( )
A、m+1 B、2m C、2 D、m+2
8. 在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3﹣xy2,取x=20,y=10,用上述方法产生的密码不可能是( )21世纪教育网版权所有
A.201010 B.203010 C.301020 D.201030
二、填空题(本大题共6小题)
9. 简便计算:7.292﹣2.712= .
10. 如图所示,根据图形把多项式a2+5ab+4b2因式分解= .
11. 已知a2﹣a﹣1=0,则a3﹣a2﹣a+2016= .
12. 若对x恒成立,则n= .
13. 在实数范围内因式分解:= .
14. 已知a2﹣6a+9与|b﹣1|互为相反数,计算a3b3+2a2b2+ab的结果是 .
三、计算题(本大题共4小题)
15. 分解因式:
(1)2a(y﹣z)﹣3b(z﹣y)
(2)﹣a4+16
(3)a2b﹣2ab+b
(4)3(x﹣2y)2﹣3x+6y.
16. 下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A、提取公因式B.平方差公式
C、两数和的完全平方公式D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底 .(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果 .
请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
17. 如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.21教育网
若h=a+b,且a,b满足a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
18. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是怎样的?写出得到公式的过程.21·cn·jy·com
参考答案:
一、选择题(本大题共8小题)
1. C
分析:根据因式分解的定义作答.把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式.21·世纪*教育网
解:A、是整式的乘法运算,故选项错误;
B、结果不是积的形式,故选项错误;
C、x2﹣1=(x+1)(x﹣1),正确;
D、结果不是积的形式,故选项错误.
故选:C.
2. D
分析;本题需先对每个式子进行因式分解,即可得出不含因式a+1的式子.
解:A、∵2a2+2a=2a(a+1),故本选项正确;
B、a2+2a+1=(a+1)2,故本选项正确;
C、a2﹣1=(a+1)(a﹣1),故本选项正确;
D、=(a+2,故本选项错误.
故选D.
3. C
分析:根据因式分解的意义解答即可.
解:设x4+mx3+nx-16=(x-1)(x-2)(x2+ax+b),则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b.www-2-1-cnjy-com
比较系数得:a-3=m,b-3a+2=0,2a-3b=n,2b=-16,解得:a=-2,b=-8,m=-5,n=20,所以mn=-5×20=-100.故选C.2-1-c-n-j-y
4.A
分析:1.平方差公式;2.整式的除法;3.因式分解-十字相乘法等;4.分式的加减法.
解:A.,正确;
B.,错误;
C.,错误;
D.,错误;故选A.
5.A
分析:根据提公因式法和完全平方公式把各选项的多项式分解因式,然后再找出结果中含有相同因式的即可.
解:①2x2﹣x=x(2x﹣1);
②(x﹣1)2﹣4(x﹣1)+4=(x﹣3)2;
③(x+1)2﹣4x(x+1)+4无法分解因式;
④﹣4x2﹣1+4x=﹣(4x2﹣4x+1)=﹣(2x﹣1)2.
所以分解因式后,结果中含有相同因式的是①和④.
故选:A.
6. B
分析:直接利用多项式乘以多项式得出等式右边多项式进而得出k的值.
解:∵x2-kx-15=(x+5)(x-3),
∴x2-kx-15=x2+2x-15,
∴-k=2,则k=-2.故选B.
7. D
分析:把多项式(m+1)(m-1)+(m-1)提取公因式(m-1)后,即可知答案.
解:(m+1)(m-1)+(m-1)=(m-1)(m+1+1)=(m-1)(m+2),故选D.
8. A
分析:对多项式利用提公因式法分解因式,利用平方差公式分解因式,然后把数值代入计算即可确定出密码.
解:x3﹣xy2=x(x2﹣y2)=x(x+y)(x﹣y),
当x=20,y=10时,x=20,x+y=30,x﹣y=10,
组成密码的数字应包括20,30,10,
所以组成的密码不可能是201010.
故选A.
二、填空题(本大题共6小题)
9.分析:根据平方差公式,a2﹣b2=(a+b)(a﹣b),即可解答出;
解:根据平方差公式得,
7.292﹣2.712=(7.29+2.71)(7.29﹣2.71),
=10×4.58,
=45.8;
故答案为:45.8.
10. 分析:根据图形和等积法可以对题目中的式子进行因式分解.
解:由图可知,
a2+5ab+4b2=(a+b)(a+4b),
故答案为:(a+b)(a+4b).
11.分析:在代数式a3﹣a2﹣a+2016中提取出a,再将a2﹣a﹣1=0代入其中即可得出结论.
解:∵a2﹣a﹣1=0,
∴a3﹣a2﹣a+2016=a(a2﹣a﹣1)+2016=0+2016=2016.
故答案为:2016.
12.分析:因式分解-十字相乘法等.
解:∵,∴,故,解得:n=4.故答案为:4.
13.分析:实数范围内分解因式.
解:原式==,故答案为:.
14.分析:根据互为相反数的性质和非负数的性质求得a,b的值,再进一步代入求解.
解:a2﹣6a+9=(a﹣3)2.依题意得
(a﹣3)2+|b﹣1|=0,则
a﹣3=0.b﹣1=0,
解得 a=3,b=1.
所以a3b3+2a2b2+ab=ab(a2b2+2ab+1)=ab(ab+1)2=3×16=48,
故答案为:48.
三、计算题(本大题共4小题)
15. 分析:(1)直接提公因式y﹣z即可;
(2)利用平方差分解后,再利用平方差进行二次分解即可;
(3)首先提公因式b,再利用完全平方公式进行分解即可;
(4)首先把后两项组合提公因式3,再提公因式3(x﹣2y)即可.
解:(1)原式=2a(y﹣z)+3b(y﹣z)=(y﹣z)(2a+3b);
(2)原式=(4﹣a2)(4+a2)=(2﹣a)(2+a)(4+a2);
(3)原式=b(a2﹣2a+1)=b(a﹣1)2;
(4)原式=3(x﹣2y)2﹣3(x﹣2y)=3(x﹣2y)(x﹣2y﹣1).
16. 分析:(1)完全平方式是两数的平方和与这两个数积的两倍的和或差;
(2)x2﹣4x+4还可以分解,所以是不彻底.
(3)按照例题的分解方法进行分解即可.
解:(1)运用了C,两数和的完全平方公式;
(2)x2﹣4x+4还可以分解,分解不彻底;
(3)设x2﹣2x=y.
(x2﹣2x)(x2﹣2x+2)+1,
=y(y+2)+1,
=y2+2y+1,
=(y+1)2,
=(x2﹣2x+1)2,
=(x﹣1)4.
17. 分析:(1)侧面四个长方形和上下两个底面也是长方形,所以折叠后能围成长方体.
(2)根据图1所标注的相关线段的长度画出其左视图;
(3)对a2+b2﹣a﹣6b+10=0进行因式分解,求得a、b的值,则易求h的值,然后由几何体的表面积计算公式进行解答.21cnjy.com
解:(1)根据该包装盒的表面展开图知,该几何体模型的名称为:长方体或底面为长方形的直棱柱.
故答案为:长方体或底面为长方形的直棱柱;
(2)如图所示:
;
(3)由题意得,(a﹣1)2+(b﹣3)2=0,
则a=2,b=3,
所以h=a+b=2+3=5.
所以表面积为:2(2×3+5×2+3×5)=62.
18. 分析:根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.www.21-cn-jy.com
解:(a﹣b)2=a2﹣2ab+b2.
∵大正方形的面积=(a﹣b)2,
还可以表示为a2﹣2ab+b2,
∴(a﹣b)2=a2﹣2ab+b2.
