18.1.2勾股定理的应用同步练习
图片预览


文档简介
沪科版八年级下册数学18.1.2勾股定理的应用同步练习
一、选择题(本大题共8小题)
1. 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
2. 如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160km,BC=120km,则A,C两村之间的距离为( )21·cn·jy·com
A.250km B.240km C.200km D.180km
3. 在长、宽、高分别为12 cm、4 cm、3 cm的木箱中,放一根木棒,能放进去的木棒的最大长度为( )【来源:21·世纪·教育·网】
A.5 cm B.12 cm C.13 cm D. cm
4. 一架长25m的云梯,斜立在一竖直的墙上,这时梯子底端距墙脚7m,如果梯子的顶端沿墙下滑了4m,那么梯子底端将滑动( )
A.8m B.5m C.13m D.15m
5. 要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为( )
A.12m B.13m C.14m D.15m
6. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
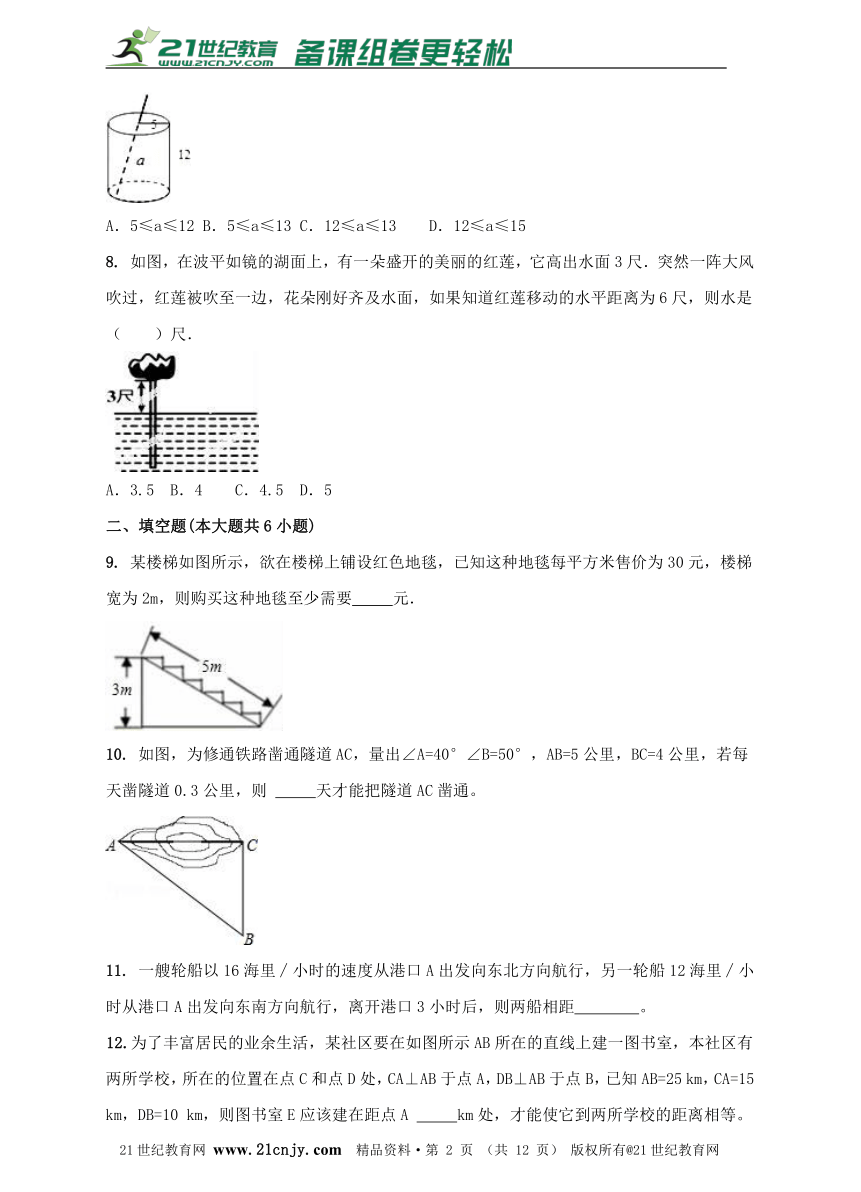
7. 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
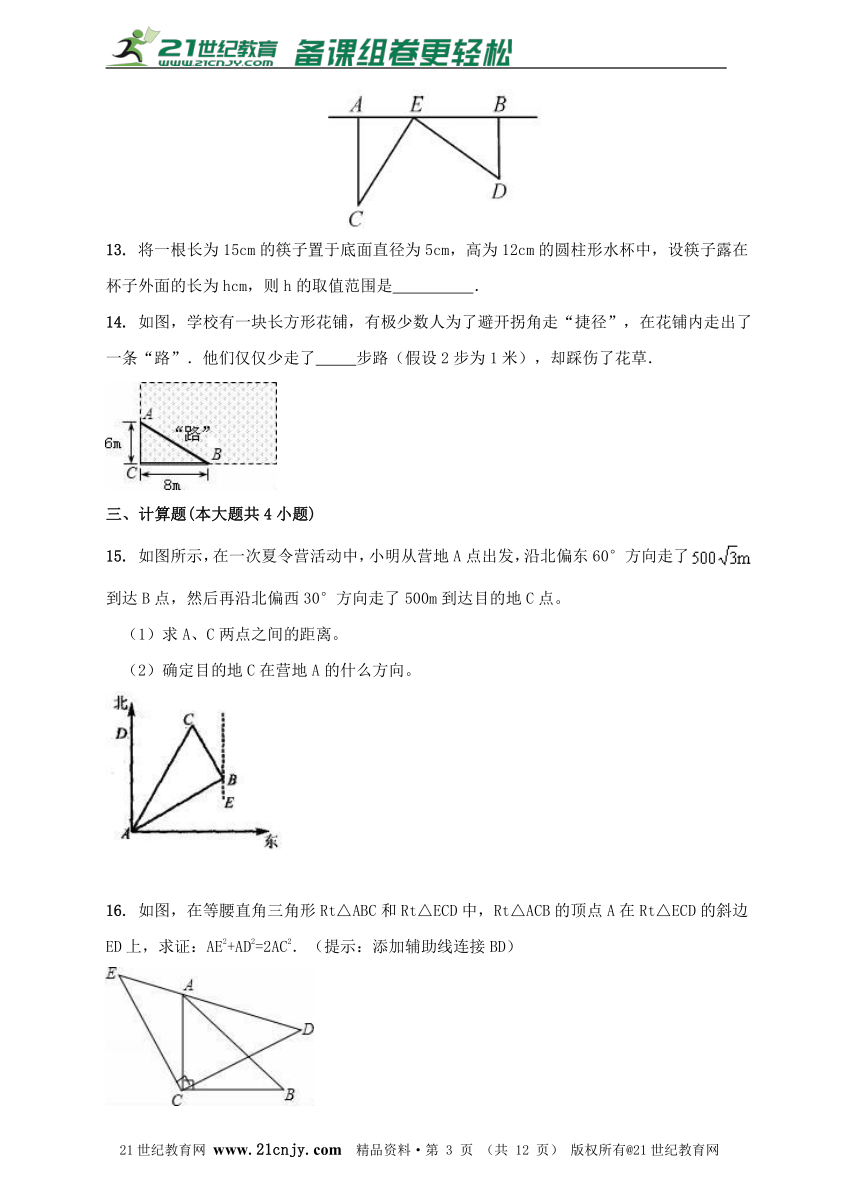
8. 如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.21·世纪*教育网
A.3.5 B.4 C.4.5 D.5
二、填空题(本大题共6小题)
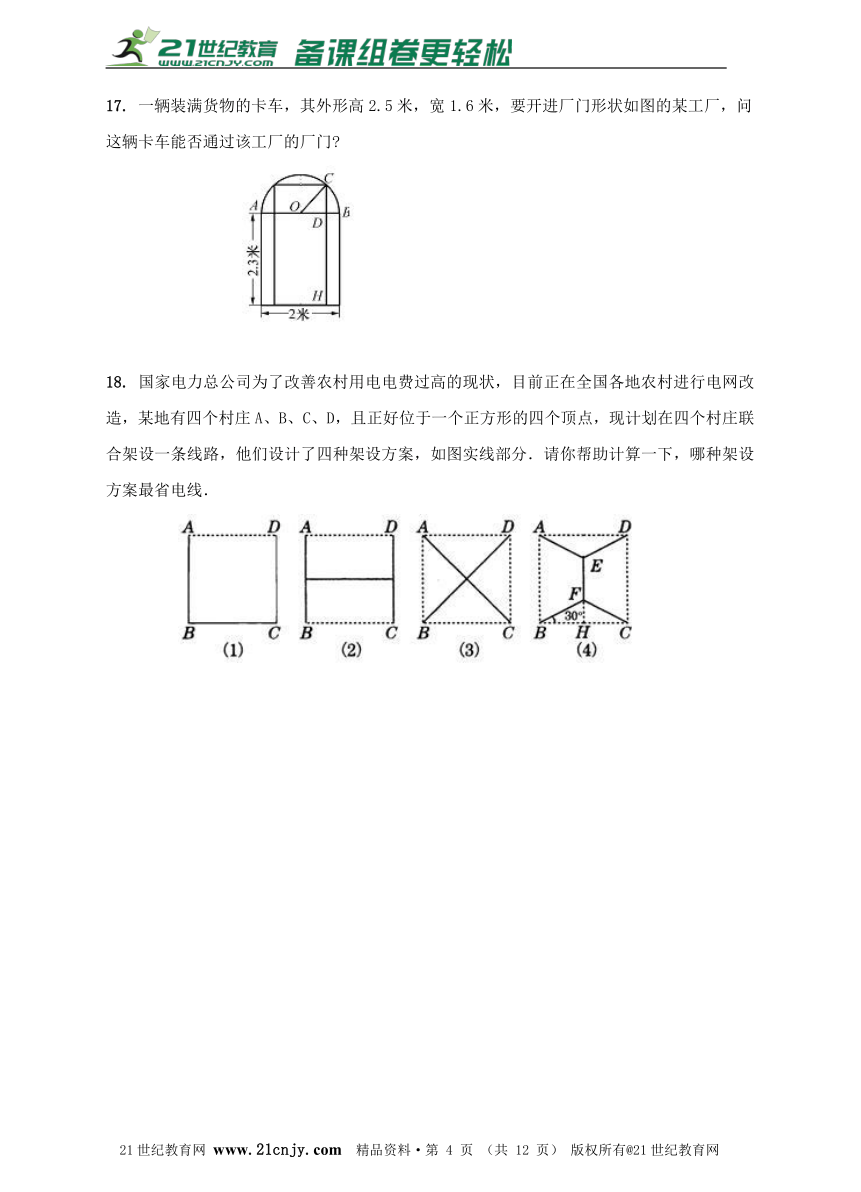
9. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 元.
10. 如图,为修通铁路凿通隧道AC,量出∠A=40°∠B=50°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,则 天才能把隧道AC凿通。2-1-c-n-j-y
11. 一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,另一轮船12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距 。
12.为了丰富居民的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,则图书室E应该建在距点A km处,才能使它到两所学校的距离相等。
13. 将一根长为15cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是 .21*cnjy*com
14. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
三、计算题(本大题共4小题)
15. 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。【来源:21cnj*y.co*m】
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
16. 如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
17. 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门? 21教育名师原创作品
18. 国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进行电网改造,某地有四个村庄A、B、C、D,且正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分.请你帮助计算一下,哪种架设方案最省电线. 21世纪教育网版权所有
参考答案:
一、选择题(本大题共8小题)
1. A
分析:由题意可知消防车的云梯长、地面、建筑物高构成一直角三角形,斜边为消防车的云梯长,根据勾股定理就可求出高度。2·1·c·n·j·y
解:,故选A。
2. B
分析:直接利用平行线的性质得出∠ABC的度数,再利用勾股定理得出答案.
解:∵MN∥EF,∠MAB=65°,
∴∠ABF=65°,
∵∠CBE=25°,
∴∠ABC=180°﹣65°﹣25°=90°,
∴△ABC是直角三角形,
∴AC==200(km).
故选:C.
3. C
分析:要判断能否放进去,关键是求得该木箱中的最长线段的长度,即AD的长,通过比较它们的大小作出判断.【版权所有:21教育】
解:解:如图,连接AC、AD.
在Rt△ABC中,有AC2=AB2+BC2=160,
在Rt△ACD中,有AD2=AC2+CD2=169,
∵AD= ,
∴能放进去的木棒的最大长度为13.故选:C.
4.A
分析:利用勾股定理进行解答.求出下滑后梯子低端距离低端的距离,再计算梯子低端滑动的距离.
解;梯子顶端距离墙角地距离为=24m,
顶端下滑后梯子低端距离墙角的距离为=15m,
15m﹣7m=8m.
故选A.
5. B
分析:如(解答)图,AB为梯子长,AC为底端离建筑物的长5m,BC为顶端离地面的长12m;根据勾股定理即可求得.
解:如图:
∵AC=5m,BC=12m,∠C=90°
∴AB==13m
故选B.
6. A
分析:仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.www-2-1-cnjy-com
解:梯脚与墙角距离: =0.7(米).
故选A.
7.C
分析:如图,当吸管底部在O点时吸管在罐内部分a最短,此时a就是圆柱形的高;当吸管底部在A点时吸管在罐内部分a最长,此时a可以利用勾股定理在Rt△ABO中即可求出.21*cnjy*com
解:当吸管底部在O点时吸管在罐内部分a最短,
此时a就是圆柱形的高,
即a=12;
当吸管底部在A点时吸管在罐内部分a最长, 即线段AB的长,
在Rt△ABO中,AB= ==13,
∴此时a=13,
所以12≤a≤13.
故答案为:12≤a≤13.故选C。
8. C
分析:仔细分析该题,可画出草图,关键是水深、红莲移动的水平距离及红莲的高度构成一直角三角形,解此直角三角形即可.【出处:21教育名师】
解:红莲被吹至一边,花朵刚好齐及水面即AC为红莲的长.
设水深h尺,由题意得:
Rt△ABC中,AB=h,AC=h+3,BC=6,
由勾股定理得:AC2=AB2+BC2,
即(h+3)2=h2+62,
解得:h=4.5.
故选:C.
二、填空题(本大题共6小题)
9. 分析:根据勾股定理可求得水平直角边的长.从而根据地毯的面积乘以每平方米的价格即可得到其所需的钱.
解:已知直角三角形的一条直角边是3m,斜边是5m,
根据勾股定理得到:水平的直角边是4m,地毯水平的部分的和是水平边的长,竖直的部分的和是竖直边的长,
则购买这种地毯的长是3m+4m=7m,则面积是14m2,
价格是14×30=420元.
10. 分析:由题意知:∠A=50°,∠B=40°则∠C为90°,在直角△ABC中,已知AB,BC根据勾股定理即可求AC,则需要天数可求.www.21-cn-jy.com
解:∵∠A=50°,∠B=40°,
∴∠C=90°,
∴AC2=AB2﹣BC2=(3km)2
∴AC=3km,
∵3÷0.3=10,
∴10天才能将隧道凿通.
11.分析:根据方位角可知两船所走的方向正好构成了直角.然后根据路程=速度×时间,得两条船分别走了48,36.再根据勾股定理,即可求得两条船之间的距离.
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得:=60(海里).
12.
解:设AE=x km,则BE=(25-x)km.
在Rt△ACE中,由勾股定理得:CE2=AE2+AC2=x2+152.
同理可得:DE2=(25-x)2+102.
若CE=DE,则
x2+152=(25-x)2+102.解得x=10.
答:图书室E应该建在距A点10 km处,才能使它到两所学校的距离相等.
13. 分析: 根据杯子内筷子的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
解:∵将一根长为15cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,h=12,
最长时等于杯子斜边长度,即:h==13,
∴h的取值范围是:(15﹣13)≤h≤(15﹣12),
即2cm≤h≤3cm.
故答案为:2cm≤h≤3cm.
14.
分析:直接利用勾股定理得出AB的长,再利用AC+BC﹣AB进而得出答案.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
三、计算题(本大题共4小题)
15.分析:可以构造直角三角形,根据勾股定理进行解答即可。
解:(1)过B点作BE//AD
∴∠DAB=∠ABE=60°
∵30°+∠CBA+∠ABE=180°
∴∠CBA=90°
即△ABC为直角三角形
由已知可得:BC=500m,AB=
由勾股定理可得:
所以
(2)在Rt△ABC中,
∵BC=500m,AC=1000m
∴∠CAB=30°
∵∠DAB=60°
∴∠DAC=30°
即点C在点A的北偏东30°的方向。
16. 分析:连结BD,根据等边三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
证明:连结BD,
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD﹣∠ACD=∠ACB﹣∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.
17.分析:结合实际情况进行构造直角三角形,利用勾股定理解答。
解:由于厂门宽度是否足够卡车通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
、 解:OC=1米 (大门宽度一半),
OD=0.8米 (卡车宽度一半)
在Rt△OCD中,由勾股定理得:
CD===0.6米,
CH=0.6+2.3=2.9(米)>2.5(米).
因此高度上有0.4米的余量,所以卡车能通过厂门.
18. 分析:解答本题的思路是:最省电线就是线路长最短,通过利用勾股定理计算线路长,然后进行比较,得出结论.21教育网
解:设正方形的边长为1,则图(1)、图(2)中的总线路长分别为
AB+BC+CD=3,AB+BC+CD=3
图(3)中,在Rt△ABC中
同理
∴图(3)中的路线长为
图(4)中,延长EF交BC于H,则FH⊥BC,BH=CH 由∠FBH= 及勾股定理得:21cnjy.com
EA=ED=FB=FC=,FH=
∴EF=1-2FH=1-
∴此图中总线路的长为4EA+EF= 3>2.828>2.732
∴图(4)的连接线路最短,即图(4)的架设方案最省电线.
一、选择题(本大题共8小题)
1. 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
2. 如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160km,BC=120km,则A,C两村之间的距离为( )21·cn·jy·com
A.250km B.240km C.200km D.180km
3. 在长、宽、高分别为12 cm、4 cm、3 cm的木箱中,放一根木棒,能放进去的木棒的最大长度为( )【来源:21·世纪·教育·网】
A.5 cm B.12 cm C.13 cm D. cm
4. 一架长25m的云梯,斜立在一竖直的墙上,这时梯子底端距墙脚7m,如果梯子的顶端沿墙下滑了4m,那么梯子底端将滑动( )
A.8m B.5m C.13m D.15m
5. 要登上某建筑物,靠墙有一架梯子,底端离建筑物5m,顶端离地面12m,则梯子的长度为( )
A.12m B.13m C.14m D.15m
6. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
7. 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
8. 如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.21·世纪*教育网
A.3.5 B.4 C.4.5 D.5
二、填空题(本大题共6小题)
9. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要 元.
10. 如图,为修通铁路凿通隧道AC,量出∠A=40°∠B=50°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,则 天才能把隧道AC凿通。2-1-c-n-j-y
11. 一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,另一轮船12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距 。
12.为了丰富居民的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,则图书室E应该建在距点A km处,才能使它到两所学校的距离相等。
13. 将一根长为15cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长为hcm,则h的取值范围是 .21*cnjy*com
14. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
三、计算题(本大题共4小题)
15. 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。【来源:21cnj*y.co*m】
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
16. 如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
17. 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门? 21教育名师原创作品
18. 国家电力总公司为了改善农村用电电费过高的现状,目前正在全国各地农村进行电网改造,某地有四个村庄A、B、C、D,且正好位于一个正方形的四个顶点,现计划在四个村庄联合架设一条线路,他们设计了四种架设方案,如图实线部分.请你帮助计算一下,哪种架设方案最省电线. 21世纪教育网版权所有
参考答案:
一、选择题(本大题共8小题)
1. A
分析:由题意可知消防车的云梯长、地面、建筑物高构成一直角三角形,斜边为消防车的云梯长,根据勾股定理就可求出高度。2·1·c·n·j·y
解:,故选A。
2. B
分析:直接利用平行线的性质得出∠ABC的度数,再利用勾股定理得出答案.
解:∵MN∥EF,∠MAB=65°,
∴∠ABF=65°,
∵∠CBE=25°,
∴∠ABC=180°﹣65°﹣25°=90°,
∴△ABC是直角三角形,
∴AC==200(km).
故选:C.
3. C
分析:要判断能否放进去,关键是求得该木箱中的最长线段的长度,即AD的长,通过比较它们的大小作出判断.【版权所有:21教育】
解:解:如图,连接AC、AD.
在Rt△ABC中,有AC2=AB2+BC2=160,
在Rt△ACD中,有AD2=AC2+CD2=169,
∵AD= ,
∴能放进去的木棒的最大长度为13.故选:C.
4.A
分析:利用勾股定理进行解答.求出下滑后梯子低端距离低端的距离,再计算梯子低端滑动的距离.
解;梯子顶端距离墙角地距离为=24m,
顶端下滑后梯子低端距离墙角的距离为=15m,
15m﹣7m=8m.
故选A.
5. B
分析:如(解答)图,AB为梯子长,AC为底端离建筑物的长5m,BC为顶端离地面的长12m;根据勾股定理即可求得.
解:如图:
∵AC=5m,BC=12m,∠C=90°
∴AB==13m
故选B.
6. A
分析:仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.www-2-1-cnjy-com
解:梯脚与墙角距离: =0.7(米).
故选A.
7.C
分析:如图,当吸管底部在O点时吸管在罐内部分a最短,此时a就是圆柱形的高;当吸管底部在A点时吸管在罐内部分a最长,此时a可以利用勾股定理在Rt△ABO中即可求出.21*cnjy*com
解:当吸管底部在O点时吸管在罐内部分a最短,
此时a就是圆柱形的高,
即a=12;
当吸管底部在A点时吸管在罐内部分a最长, 即线段AB的长,
在Rt△ABO中,AB= ==13,
∴此时a=13,
所以12≤a≤13.
故答案为:12≤a≤13.故选C。
8. C
分析:仔细分析该题,可画出草图,关键是水深、红莲移动的水平距离及红莲的高度构成一直角三角形,解此直角三角形即可.【出处:21教育名师】
解:红莲被吹至一边,花朵刚好齐及水面即AC为红莲的长.
设水深h尺,由题意得:
Rt△ABC中,AB=h,AC=h+3,BC=6,
由勾股定理得:AC2=AB2+BC2,
即(h+3)2=h2+62,
解得:h=4.5.
故选:C.
二、填空题(本大题共6小题)
9. 分析:根据勾股定理可求得水平直角边的长.从而根据地毯的面积乘以每平方米的价格即可得到其所需的钱.
解:已知直角三角形的一条直角边是3m,斜边是5m,
根据勾股定理得到:水平的直角边是4m,地毯水平的部分的和是水平边的长,竖直的部分的和是竖直边的长,
则购买这种地毯的长是3m+4m=7m,则面积是14m2,
价格是14×30=420元.
10. 分析:由题意知:∠A=50°,∠B=40°则∠C为90°,在直角△ABC中,已知AB,BC根据勾股定理即可求AC,则需要天数可求.www.21-cn-jy.com
解:∵∠A=50°,∠B=40°,
∴∠C=90°,
∴AC2=AB2﹣BC2=(3km)2
∴AC=3km,
∵3÷0.3=10,
∴10天才能将隧道凿通.
11.分析:根据方位角可知两船所走的方向正好构成了直角.然后根据路程=速度×时间,得两条船分别走了48,36.再根据勾股定理,即可求得两条船之间的距离.
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
两小时后,两艘船分别行驶了16×3=48,12×3=36海里,
根据勾股定理得:=60(海里).
12.
解:设AE=x km,则BE=(25-x)km.
在Rt△ACE中,由勾股定理得:CE2=AE2+AC2=x2+152.
同理可得:DE2=(25-x)2+102.
若CE=DE,则
x2+152=(25-x)2+102.解得x=10.
答:图书室E应该建在距A点10 km处,才能使它到两所学校的距离相等.
13. 分析: 根据杯子内筷子的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
解:∵将一根长为15cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,h=12,
最长时等于杯子斜边长度,即:h==13,
∴h的取值范围是:(15﹣13)≤h≤(15﹣12),
即2cm≤h≤3cm.
故答案为:2cm≤h≤3cm.
14.
分析:直接利用勾股定理得出AB的长,再利用AC+BC﹣AB进而得出答案.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
三、计算题(本大题共4小题)
15.分析:可以构造直角三角形,根据勾股定理进行解答即可。
解:(1)过B点作BE//AD
∴∠DAB=∠ABE=60°
∵30°+∠CBA+∠ABE=180°
∴∠CBA=90°
即△ABC为直角三角形
由已知可得:BC=500m,AB=
由勾股定理可得:
所以
(2)在Rt△ABC中,
∵BC=500m,AC=1000m
∴∠CAB=30°
∵∠DAB=60°
∴∠DAC=30°
即点C在点A的北偏东30°的方向。
16. 分析:连结BD,根据等边三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
证明:连结BD,
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD﹣∠ACD=∠ACB﹣∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.
17.分析:结合实际情况进行构造直角三角形,利用勾股定理解答。
解:由于厂门宽度是否足够卡车通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
、 解:OC=1米 (大门宽度一半),
OD=0.8米 (卡车宽度一半)
在Rt△OCD中,由勾股定理得:
CD===0.6米,
CH=0.6+2.3=2.9(米)>2.5(米).
因此高度上有0.4米的余量,所以卡车能通过厂门.
18. 分析:解答本题的思路是:最省电线就是线路长最短,通过利用勾股定理计算线路长,然后进行比较,得出结论.21教育网
解:设正方形的边长为1,则图(1)、图(2)中的总线路长分别为
AB+BC+CD=3,AB+BC+CD=3
图(3)中,在Rt△ABC中
同理
∴图(3)中的路线长为
图(4)中,延长EF交BC于H,则FH⊥BC,BH=CH 由∠FBH= 及勾股定理得:21cnjy.com
EA=ED=FB=FC=,FH=
∴EF=1-2FH=1-
∴此图中总线路的长为4EA+EF= 3>2.828>2.732
∴图(4)的连接线路最短,即图(4)的架设方案最省电线.
