河北省张家口市万全中学2016-2017学年八年级(上)第一次月考数学试卷(解析版)
文档属性
| 名称 | 河北省张家口市万全中学2016-2017学年八年级(上)第一次月考数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-03 00:00:00 | ||
图片预览



文档简介
2016-2017学年河北省张家口市万全中学八年级(上)第一次月考数学试卷
一、选择题(共14小题,每小题3分,共42分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的代号填在答卷指定位置.
1.下列二次根式中,属于最简二次根式的是( )
A.
B.
C.
D.
2.要使式子有意义,则x的取值范围是( )
A.x>0
B.x≥﹣2
C.x≥2
D.x≤2
3.下列二次根式,不能与合并的是( )
A.
B.
C.
D.
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2
B.36cm2
C.48cm2
D.60cm2
5.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12
B.10
C.7.5
D.5
6.分别以下列五组数为一个三角形的边长:①6,8,10
②13,5,12
③1,2,3
④9,40,41
⑤3,4,5.其中能构成直角三角形的有( )组.
A.2
B.3
C.4
D.5
7.已知a=2﹣,b=,则a、b的关系为( )
A.相等
B.互为相反数
C.互为倒数
D.互为负倒数
8.如图所示,要在离地面5米处引拉线固定电线杆,使拉线和地面成45°角.若要考虑既要符合设计要求,又要节省材料,则在库存的L1=5.2米,L2=6.2米,L3=7.2米,L4=10米四种备用拉线材料中,拉线AC最好选用( )
A.L1
B.L2
C.L3
D.L4
9.如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1=S2
B.S1<S2
C.S1>S2
D.无法确定
10.如图,在周长为26cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
11.如图,长方形ABCD中,E点在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC面积为( )
A.15
B.30
C.45
D.60
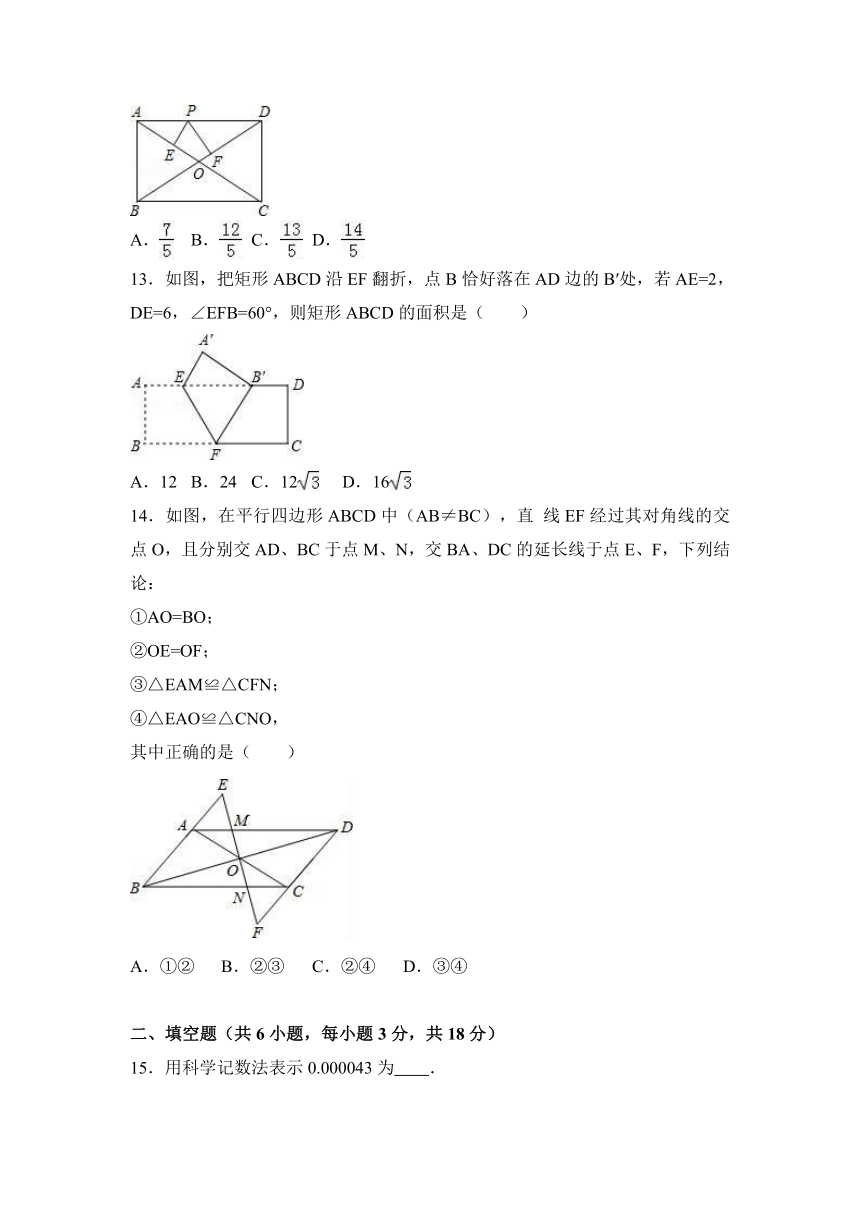
12.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于( )
A.
B.
C.
D.
13.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12
B.24
C.12
D.16
14.如图,在平行四边形ABCD中(AB≠BC),直
线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①AO=BO;
②OE=OF;
③△EAM≌△CFN;
④△EAO≌△CNO,
其中正确的是( )
A.①②
B.②③
C.②④
D.③④
二、填空题(共6小题,每小题3分,共18分)
15.用科学记数法表示0.000043为 .
16.如图,数轴上的点A所表示的数为x,则x2﹣10的立方根为 .
17.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为 .
18.已知y=++5,则x2﹣xy+y2= .
19.命题“同位角相等,两直线平行”的逆命题是: .
20.观察下列各式:
=2,
=3,
=4,…请你找出其中规律,并将第n(n≥1)个等式写出来 .
三、解答题(共6小题,每小题12分,共14分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.
21.计算:
(1)+2﹣(﹣)
(2)(﹣4)﹣(3﹣2)
(3)(2+)2﹣(+)(﹣)
22.先化简,再求值:(﹣)÷,其中x=2.
23.矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,
(1)求AB;
(2)求AD;
(3)求矩形ABCD的面积.
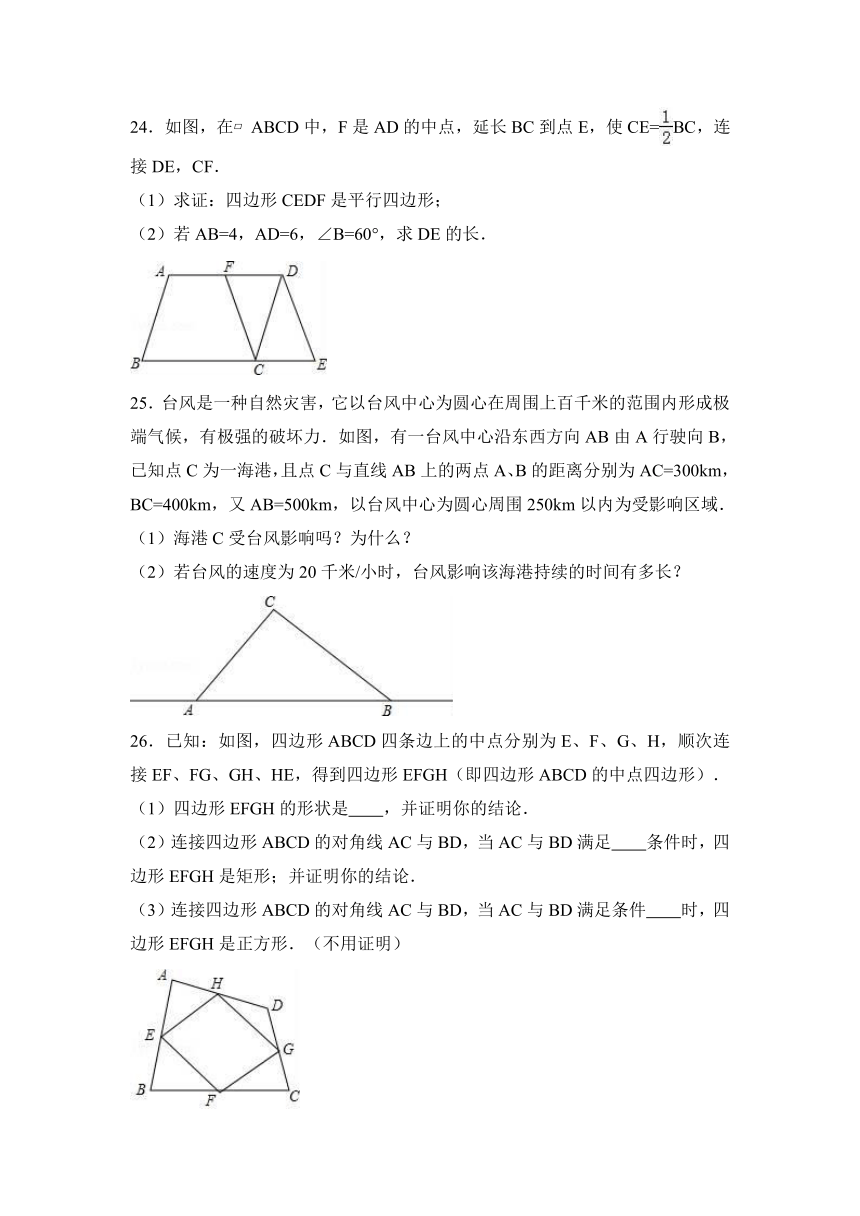
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
25.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
26.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 ,并证明你的结论.
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足 条件时,四边形EFGH是矩形;并证明你的结论.
(3)连接四边形ABCD的对角线AC与BD,当AC与BD满足条件 时,四边形EFGH是正方形.(不用证明)
2016-2017学年河北省张家口市万全中学八年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题(共14小题,每小题3分,共42分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的代号填在答卷指定位置.
1.下列二次根式中,属于最简二次根式的是( )
A.
B.
C.
D.
【考点】最简二次根式.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【解答】解:A、被开方数含分母,故A错误;
B、被开方数含分母,故B错误;
C、被开方数含能开得尽方的因数,故C错误;
D、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
2.要使式子有意义,则x的取值范围是( )
A.x>0
B.x≥﹣2
C.x≥2
D.x≤2
【考点】二次根式有意义的条件.
【分析】根据被开方数大于等于0列式计算即可得解.
【解答】解:根据题意得,2﹣x≥0,
解得x≤2.
故选D.
3.下列二次根式,不能与合并的是( )
A.
B.
C.
D.
【考点】同类二次根式.
【分析】把各二次根式化简,然后根据不能合并的不是同类二次根式进行判断即可.
【解答】解:
=2,
A、=4,能合并,故本选项错误;
B、=3,不能合并,故本选项正确;
C、==,能合并,故本选项错误;
D、﹣=﹣5,能合并,故本选项错误.
故选B.
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2
B.36cm2
C.48cm2
D.60cm2
【考点】勾股定理;完全平方公式.
【分析】要求Rt△ABC的面积,只需求出两条直角边的乘积.根据勾股定理,得a2+b2=c2=100.根据勾股定理就可以求出ab的值,进而得到三角形的面积.
【解答】解:∵a+b=14
∴(a+b)2=196
∴2ab=196﹣(a2+b2)=96
∴ab=24.
故选A.
5.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12
B.10
C.7.5
D.5
【考点】矩形的性质.
【分析】如下图所示:∠AOD=∠BOC=60°,即:∠COD=120°>∠AOD=60°,AD是该矩形较短的一边,根据矩形的性质:矩形的对角线相等且互相平分,所以有OA=OD=OC=OB=7.5,又因为∠AOD=∠BOC=60°,所以AD的长即可求出.
【解答】解:如下图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选C.
6.分别以下列五组数为一个三角形的边长:①6,8,10
②13,5,12
③1,2,3
④9,40,41
⑤3,4,5.其中能构成直角三角形的有( )组.
A.2
B.3
C.4
D.5
【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
【解答】解:因为①62+82=102,②132=52+122,④92+402=412,符合勾股定理的逆定理,所以能构成直角三角形的有三组.故选B.
7.已知a=2﹣,b=,则a、b的关系为( )
A.相等
B.互为相反数
C.互为倒数
D.互为负倒数
【考点】实数的性质;分母有理化.
【分析】根据乘积为1的两个数互为倒数,可得答案.
【解答】解:(2﹣)(2+)=1,故a、b互为倒数,
故选:C.
8.如图所示,要在离地面5米处引拉线固定电线杆,使拉线和地面成45°角.若要考虑既要符合设计要求,又要节省材料,则在库存的L1=5.2米,L2=6.2米,L3=7.2米,L4=10米四种备用拉线材料中,拉线AC最好选用( )
A.L1
B.L2
C.L3
D.L4
【考点】勾股定理的应用.
【分析】先利用勾股定理计算出AC,然后进行无理数估算后进行判断.
【解答】解:在Rt△ACD中,∵AD=5,CD=5,
∴AC==5≈7.07,
∴拉线AC最好选用L3.
故选C.
9.如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1=S2
B.S1<S2
C.S1>S2
D.无法确定
【考点】勾股定理.
【分析】因为是直角三角形,所以可以直接运用勾股定理,然后运用圆的面积公式来求解.
【解答】解:∵△ABC为直角三角形,
∴AB2=AC2+BC2
又∵
∴S1=π=π ,
=()=π =S1
∴S1=S2,
故选A.
10.如图,在周长为26cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
【考点】平行四边形的性质.
【分析】由平行四边形的性质和已知条件求出AB+AD=13cm,由线段垂直平分线的性质得出BE=DE,得出△ABE的周长=AB+BE+AE=AB+AD=13cm即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
∵ ABCD的周长为26cm,
∴AB+AD=13cm,
∵OE⊥BD,
∴BE=DE,
∴△ABE的周长=AB+BE+AE=AB+DE+AE=AB+AD=13cm;
故选:D.
11.如图,长方形ABCD中,E点在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC面积为( )
A.15
B.30
C.45
D.60
【考点】矩形的性质.
【分析】利用角平分线的性质定理可得AC边上的高.进而求得所求三角形的面积.
【解答】解:作EF⊥AC于点F.
∴BE=EF=4.
∴△AEC面积=15×4÷2=30.
故选B.
12.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于( )
A.
B.
C.
D.
【考点】矩形的性质;三角形的面积;勾股定理.
【分析】连接OP,过D作DM⊥AC于M,求出AC长,根据三角形的面积公式求出CM的值,根据S△AOD=S△APO+S△DPO代入求出PE+PF=DM即可.
【解答】解:连接OP,过D作DM⊥AC于M,
∵四边形ABCD是矩形,
∴AO=OC=AC,OD=OB=BD,AC=BD,∠ADC=90°
∴OA=OD,
由勾股定理得:AC==5,
∵S△ADC=×3×4=×5×DM,
∴DM=,
∵S△AOD=S△APO+S△DPO,
∴(AO×DM)=(AO×PE)+(DO×PF),
即PE+PF=DM=,
故选B.
13.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12
B.24
C.12
D.16
【考点】翻折变换(折叠问题);矩形的性质.
【分析】根据平行线的性质和折叠的性质易证得△EFB′是等边三角形,继而可得△A′B′E中,B′E=2A′E,则可求得B′E的长,然后由勾股定理求得A′B′的长,继而求得答案.
【解答】解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB′=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2,即AB=2,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=AB AD=2×8=16.
故答案为:16.
14.如图,在平行四边形ABCD中(AB≠BC),直
线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①AO=BO;
②OE=OF;
③△EAM≌△CFN;
④△EAO≌△CNO,
其中正确的是( )
A.①②
B.②③
C.②④
D.③④
【考点】平行四边形的性质;全等三角形的判定与性质.
【分析】①根据平行四边形的对边相等的性质即可求得AO≠BO,即可求得①错误;
②易证△AOE≌△COF,即可求得EO=FO;
③根据相似三角形的判定即可求得△EAM∽△EBN;
④易证△EAO≌△FCO,而△FCO和△CNO不全等,根据全等三角形的传递性即可判定该选项错误.
【解答】解:①平行四边形中邻边垂直则该平行四边形为矩形,故本题中AC≠BD,即AO≠BO,故①错误;
②∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,
∴∠E=∠F,
在△AOE和△COF中,
∵,
∴△AOE≌△COF(AAS),
∴OE=OF,
故②正确;
③由②知,△AOE≌△COF,则∠A=∠F、AE=CF.
在△EAM与△CFN中,,
∴△EAM≌△CFN(ASA),
故③正确;
④∵△AOE≌△COF,且△FCO和△CNO不全等,
故△EAO和△CNO不全等,故④错误,
即②③正确.
故选B.
二、填空题(共6小题,每小题3分,共18分)
15.用科学记数法表示0.000043为 4.3×10﹣5 .
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000
043=4.3×10﹣5;
故答案为:4.3×10﹣5.
16.如图,数轴上的点A所表示的数为x,则x2﹣10的立方根为 ﹣ .
【考点】勾股定理;立方根;实数与数轴.
【分析】先根据数轴可得x的值,进而可得则x2﹣10的值,再根据立方根的定义即可求得其立方根.
【解答】解:读图可得:点A表示的数为1﹣,
即x=1﹣;
则x2﹣10=3﹣2﹣10=﹣7﹣2,
则它的立方根为﹣.
故答案为:﹣.
17.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为 .
【考点】勾股定理;直角三角形斜边上的中线;勾股定理的逆定理.
【分析】本题考查勾股定理的逆定理和直角三角形的性质,利用了勾股定理的逆定理和直角三角形的性质求解.
【解答】解:观察图形
AB==,AC==3,BC==2
∴AC2+BC2=AB2,∴三角形为直角三角形,
∵直角三角形中斜边上的中线等于斜边的一半
∴CD=.
18.已知y=++5,则x2﹣xy+y2= 19 .
【考点】二次根式有意义的条件.
【分析】先结合二次根式有意义的条件求出x和y的值,然后代入求解即可.
【解答】解:∵y=++5,
∴x﹣3≥0,3﹣x≥0,
∴x=3,
y=5,
∴x2﹣xy+y2=9﹣15+25=19.
故答案为:19.
19.命题“同位角相等,两直线平行”的逆命题是: 两直线平行,同位角相等 .
【考点】命题与定理.
【分析】把一个命题的题设和结论互换就得到它的逆命题.
【解答】解:命题:“同位角相等,两直线平行.”的题设是“同位角相等”,结论是“两直线平行”.
所以它的逆命题是“两直线平行,同位角相等.”
故答案为:“两直线平行,同位角相等”.
20.观察下列各式:
=2,
=3,
=4,…请你找出其中规律,并将第n(n≥1)个等式写出来 .
【考点】算术平方根.
【分析】根据所给例子,找到规律,即可解答.
【解答】解:
=(1+1)=2,
=(2+1)=3,
=(3+1)=4,
…
,
故答案为:.
三、解答题(共6小题,每小题12分,共14分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.
21.计算:
(1)+2﹣(﹣)
(2)(﹣4)﹣(3﹣2)
(3)(2+)2﹣(+)(﹣)
【考点】二次根式的混合运算.
【分析】(1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先把各二次根式化简为最简二次根式,然后合并即可;
(3)利用完全平方公式和平方差公式计算.
【解答】解:(1)原式=2+2﹣3+
=3﹣;
(2)原式=4﹣﹣+
=3;
(3)原式=20+4+3﹣(5﹣2)
=23+4﹣3
=20+4.
22.先化简,再求值:(﹣)÷,其中x=2.
【考点】分式的化简求值.
【分析】按照分式的性质进行化简后代入x=2求值即可.
【解答】解:原式=
=
当x=2时,原式=.
23.矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,
(1)求AB;
(2)求AD;
(3)求矩形ABCD的面积.
【考点】矩形的性质.
【分析】(1)由矩形ABCD中,∠AOB=60°,易得△AOB是等边三角形,又由AC=10,则可求得OA的长,继而求得答案;
(2)在Rt△ABD中,直接利用勾股定理求解即可求得答案;
(3)由S矩形ABCD=AD AB,即可求得答案.
【解答】解:(1)∵矩形ABCD中,AC=10,
∴OA=AC=5,BD=AC=10,
∴OB=BD=5,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=5;
(2)∵∠BAD=90°,
∴AD===5;
(3)S矩形ABCD=AD AB=25.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
【考点】平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
【分析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
【解答】证明:(1)在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=.
又∵CE=BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=CD=2,DH=2.
在 CEDF中,CE=DF=AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE==.
25.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
【考点】勾股定理的应用.
【分析】(1)利用勾股定理的逆定理得出△ABC是直角三角形,进而利用三角形面积得出CD的长,进而得出海港C是否受台风影响;
(2)利用勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间.
【解答】解:(1)海港C受台风影响,
理由:过点C作CD⊥AB,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时),
答:台风影响该海港持续的时间为7小时.
26.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 平行四边形 ,并证明你的结论.
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足 AC⊥BD 条件时,四边形EFGH是矩形;并证明你的结论.
(3)连接四边形ABCD的对角线AC与BD,当AC与BD满足条件 AC⊥BD且AC=BD 时,四边形EFGH是正方形.(不用证明)
【考点】中点四边形.
【分析】(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=BD,FG∥BD,FG═BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)根据邻边相等的矩形为正方形进行解答.
【解答】解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=BD,
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
故答案是:平行四边形;
(2)当AC⊥BD时,四边形EFGH是矩形.理由如下:
如图,连结AC.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案是:AC⊥BD;
(3)当AC⊥BD且AC=BD时,四边形EFGH是正方形.
故答案是:AC⊥BD且AC=BD.
2017年3月3日
一、选择题(共14小题,每小题3分,共42分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的代号填在答卷指定位置.
1.下列二次根式中,属于最简二次根式的是( )
A.
B.
C.
D.
2.要使式子有意义,则x的取值范围是( )
A.x>0
B.x≥﹣2
C.x≥2
D.x≤2
3.下列二次根式,不能与合并的是( )
A.
B.
C.
D.
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2
B.36cm2
C.48cm2
D.60cm2
5.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12
B.10
C.7.5
D.5
6.分别以下列五组数为一个三角形的边长:①6,8,10
②13,5,12
③1,2,3
④9,40,41
⑤3,4,5.其中能构成直角三角形的有( )组.
A.2
B.3
C.4
D.5
7.已知a=2﹣,b=,则a、b的关系为( )
A.相等
B.互为相反数
C.互为倒数
D.互为负倒数
8.如图所示,要在离地面5米处引拉线固定电线杆,使拉线和地面成45°角.若要考虑既要符合设计要求,又要节省材料,则在库存的L1=5.2米,L2=6.2米,L3=7.2米,L4=10米四种备用拉线材料中,拉线AC最好选用( )
A.L1
B.L2
C.L3
D.L4
9.如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1=S2
B.S1<S2
C.S1>S2
D.无法确定
10.如图,在周长为26cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
11.如图,长方形ABCD中,E点在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC面积为( )
A.15
B.30
C.45
D.60
12.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于( )
A.
B.
C.
D.
13.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12
B.24
C.12
D.16
14.如图,在平行四边形ABCD中(AB≠BC),直
线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①AO=BO;
②OE=OF;
③△EAM≌△CFN;
④△EAO≌△CNO,
其中正确的是( )
A.①②
B.②③
C.②④
D.③④
二、填空题(共6小题,每小题3分,共18分)
15.用科学记数法表示0.000043为 .
16.如图,数轴上的点A所表示的数为x,则x2﹣10的立方根为 .
17.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为 .
18.已知y=++5,则x2﹣xy+y2= .
19.命题“同位角相等,两直线平行”的逆命题是: .
20.观察下列各式:
=2,
=3,
=4,…请你找出其中规律,并将第n(n≥1)个等式写出来 .
三、解答题(共6小题,每小题12分,共14分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.
21.计算:
(1)+2﹣(﹣)
(2)(﹣4)﹣(3﹣2)
(3)(2+)2﹣(+)(﹣)
22.先化简,再求值:(﹣)÷,其中x=2.
23.矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,
(1)求AB;
(2)求AD;
(3)求矩形ABCD的面积.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
25.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
26.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 ,并证明你的结论.
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足 条件时,四边形EFGH是矩形;并证明你的结论.
(3)连接四边形ABCD的对角线AC与BD,当AC与BD满足条件 时,四边形EFGH是正方形.(不用证明)
2016-2017学年河北省张家口市万全中学八年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题(共14小题,每小题3分,共42分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的代号填在答卷指定位置.
1.下列二次根式中,属于最简二次根式的是( )
A.
B.
C.
D.
【考点】最简二次根式.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【解答】解:A、被开方数含分母,故A错误;
B、被开方数含分母,故B错误;
C、被开方数含能开得尽方的因数,故C错误;
D、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故D正确;
故选:D.
2.要使式子有意义,则x的取值范围是( )
A.x>0
B.x≥﹣2
C.x≥2
D.x≤2
【考点】二次根式有意义的条件.
【分析】根据被开方数大于等于0列式计算即可得解.
【解答】解:根据题意得,2﹣x≥0,
解得x≤2.
故选D.
3.下列二次根式,不能与合并的是( )
A.
B.
C.
D.
【考点】同类二次根式.
【分析】把各二次根式化简,然后根据不能合并的不是同类二次根式进行判断即可.
【解答】解:
=2,
A、=4,能合并,故本选项错误;
B、=3,不能合并,故本选项正确;
C、==,能合并,故本选项错误;
D、﹣=﹣5,能合并,故本选项错误.
故选B.
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2
B.36cm2
C.48cm2
D.60cm2
【考点】勾股定理;完全平方公式.
【分析】要求Rt△ABC的面积,只需求出两条直角边的乘积.根据勾股定理,得a2+b2=c2=100.根据勾股定理就可以求出ab的值,进而得到三角形的面积.
【解答】解:∵a+b=14
∴(a+b)2=196
∴2ab=196﹣(a2+b2)=96
∴ab=24.
故选A.
5.矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )
A.12
B.10
C.7.5
D.5
【考点】矩形的性质.
【分析】如下图所示:∠AOD=∠BOC=60°,即:∠COD=120°>∠AOD=60°,AD是该矩形较短的一边,根据矩形的性质:矩形的对角线相等且互相平分,所以有OA=OD=OC=OB=7.5,又因为∠AOD=∠BOC=60°,所以AD的长即可求出.
【解答】解:如下图所示:矩形ABCD,对角线AC=BD=15,∠AOD=∠BOC=60°
∵四边形ABCD是矩形
∴OA=OD=OC=OB=×15=7.5(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=7.5,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为7.5,
故选C.
6.分别以下列五组数为一个三角形的边长:①6,8,10
②13,5,12
③1,2,3
④9,40,41
⑤3,4,5.其中能构成直角三角形的有( )组.
A.2
B.3
C.4
D.5
【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
【解答】解:因为①62+82=102,②132=52+122,④92+402=412,符合勾股定理的逆定理,所以能构成直角三角形的有三组.故选B.
7.已知a=2﹣,b=,则a、b的关系为( )
A.相等
B.互为相反数
C.互为倒数
D.互为负倒数
【考点】实数的性质;分母有理化.
【分析】根据乘积为1的两个数互为倒数,可得答案.
【解答】解:(2﹣)(2+)=1,故a、b互为倒数,
故选:C.
8.如图所示,要在离地面5米处引拉线固定电线杆,使拉线和地面成45°角.若要考虑既要符合设计要求,又要节省材料,则在库存的L1=5.2米,L2=6.2米,L3=7.2米,L4=10米四种备用拉线材料中,拉线AC最好选用( )
A.L1
B.L2
C.L3
D.L4
【考点】勾股定理的应用.
【分析】先利用勾股定理计算出AC,然后进行无理数估算后进行判断.
【解答】解:在Rt△ACD中,∵AD=5,CD=5,
∴AC==5≈7.07,
∴拉线AC最好选用L3.
故选C.
9.如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1=S2
B.S1<S2
C.S1>S2
D.无法确定
【考点】勾股定理.
【分析】因为是直角三角形,所以可以直接运用勾股定理,然后运用圆的面积公式来求解.
【解答】解:∵△ABC为直角三角形,
∴AB2=AC2+BC2
又∵
∴S1=π=π ,
=()=π =S1
∴S1=S2,
故选A.
10.如图,在周长为26cm的 ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm
B.6cm
C.8cm
D.10cm
【考点】平行四边形的性质.
【分析】由平行四边形的性质和已知条件求出AB+AD=13cm,由线段垂直平分线的性质得出BE=DE,得出△ABE的周长=AB+BE+AE=AB+AD=13cm即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
∵ ABCD的周长为26cm,
∴AB+AD=13cm,
∵OE⊥BD,
∴BE=DE,
∴△ABE的周长=AB+BE+AE=AB+DE+AE=AB+AD=13cm;
故选:D.
11.如图,长方形ABCD中,E点在BC上,且AE平分∠BAC.若BE=4,AC=15,则△AEC面积为( )
A.15
B.30
C.45
D.60
【考点】矩形的性质.
【分析】利用角平分线的性质定理可得AC边上的高.进而求得所求三角形的面积.
【解答】解:作EF⊥AC于点F.
∴BE=EF=4.
∴△AEC面积=15×4÷2=30.
故选B.
12.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于( )
A.
B.
C.
D.
【考点】矩形的性质;三角形的面积;勾股定理.
【分析】连接OP,过D作DM⊥AC于M,求出AC长,根据三角形的面积公式求出CM的值,根据S△AOD=S△APO+S△DPO代入求出PE+PF=DM即可.
【解答】解:连接OP,过D作DM⊥AC于M,
∵四边形ABCD是矩形,
∴AO=OC=AC,OD=OB=BD,AC=BD,∠ADC=90°
∴OA=OD,
由勾股定理得:AC==5,
∵S△ADC=×3×4=×5×DM,
∴DM=,
∵S△AOD=S△APO+S△DPO,
∴(AO×DM)=(AO×PE)+(DO×PF),
即PE+PF=DM=,
故选B.
13.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12
B.24
C.12
D.16
【考点】翻折变换(折叠问题);矩形的性质.
【分析】根据平行线的性质和折叠的性质易证得△EFB′是等边三角形,继而可得△A′B′E中,B′E=2A′E,则可求得B′E的长,然后由勾股定理求得A′B′的长,继而求得答案.
【解答】解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB′=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等边三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2,即AB=2,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=AB AD=2×8=16.
故答案为:16.
14.如图,在平行四边形ABCD中(AB≠BC),直
线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①AO=BO;
②OE=OF;
③△EAM≌△CFN;
④△EAO≌△CNO,
其中正确的是( )
A.①②
B.②③
C.②④
D.③④
【考点】平行四边形的性质;全等三角形的判定与性质.
【分析】①根据平行四边形的对边相等的性质即可求得AO≠BO,即可求得①错误;
②易证△AOE≌△COF,即可求得EO=FO;
③根据相似三角形的判定即可求得△EAM∽△EBN;
④易证△EAO≌△FCO,而△FCO和△CNO不全等,根据全等三角形的传递性即可判定该选项错误.
【解答】解:①平行四边形中邻边垂直则该平行四边形为矩形,故本题中AC≠BD,即AO≠BO,故①错误;
②∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,
∴∠E=∠F,
在△AOE和△COF中,
∵,
∴△AOE≌△COF(AAS),
∴OE=OF,
故②正确;
③由②知,△AOE≌△COF,则∠A=∠F、AE=CF.
在△EAM与△CFN中,,
∴△EAM≌△CFN(ASA),
故③正确;
④∵△AOE≌△COF,且△FCO和△CNO不全等,
故△EAO和△CNO不全等,故④错误,
即②③正确.
故选B.
二、填空题(共6小题,每小题3分,共18分)
15.用科学记数法表示0.000043为 4.3×10﹣5 .
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000
043=4.3×10﹣5;
故答案为:4.3×10﹣5.
16.如图,数轴上的点A所表示的数为x,则x2﹣10的立方根为 ﹣ .
【考点】勾股定理;立方根;实数与数轴.
【分析】先根据数轴可得x的值,进而可得则x2﹣10的值,再根据立方根的定义即可求得其立方根.
【解答】解:读图可得:点A表示的数为1﹣,
即x=1﹣;
则x2﹣10=3﹣2﹣10=﹣7﹣2,
则它的立方根为﹣.
故答案为:﹣.
17.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为 .
【考点】勾股定理;直角三角形斜边上的中线;勾股定理的逆定理.
【分析】本题考查勾股定理的逆定理和直角三角形的性质,利用了勾股定理的逆定理和直角三角形的性质求解.
【解答】解:观察图形
AB==,AC==3,BC==2
∴AC2+BC2=AB2,∴三角形为直角三角形,
∵直角三角形中斜边上的中线等于斜边的一半
∴CD=.
18.已知y=++5,则x2﹣xy+y2= 19 .
【考点】二次根式有意义的条件.
【分析】先结合二次根式有意义的条件求出x和y的值,然后代入求解即可.
【解答】解:∵y=++5,
∴x﹣3≥0,3﹣x≥0,
∴x=3,
y=5,
∴x2﹣xy+y2=9﹣15+25=19.
故答案为:19.
19.命题“同位角相等,两直线平行”的逆命题是: 两直线平行,同位角相等 .
【考点】命题与定理.
【分析】把一个命题的题设和结论互换就得到它的逆命题.
【解答】解:命题:“同位角相等,两直线平行.”的题设是“同位角相等”,结论是“两直线平行”.
所以它的逆命题是“两直线平行,同位角相等.”
故答案为:“两直线平行,同位角相等”.
20.观察下列各式:
=2,
=3,
=4,…请你找出其中规律,并将第n(n≥1)个等式写出来 .
【考点】算术平方根.
【分析】根据所给例子,找到规律,即可解答.
【解答】解:
=(1+1)=2,
=(2+1)=3,
=(3+1)=4,
…
,
故答案为:.
三、解答题(共6小题,每小题12分,共14分)下列各题需要在答题卷指定位置写出文字说明、证明过程或计算步骤.
21.计算:
(1)+2﹣(﹣)
(2)(﹣4)﹣(3﹣2)
(3)(2+)2﹣(+)(﹣)
【考点】二次根式的混合运算.
【分析】(1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先把各二次根式化简为最简二次根式,然后合并即可;
(3)利用完全平方公式和平方差公式计算.
【解答】解:(1)原式=2+2﹣3+
=3﹣;
(2)原式=4﹣﹣+
=3;
(3)原式=20+4+3﹣(5﹣2)
=23+4﹣3
=20+4.
22.先化简,再求值:(﹣)÷,其中x=2.
【考点】分式的化简求值.
【分析】按照分式的性质进行化简后代入x=2求值即可.
【解答】解:原式=
=
当x=2时,原式=.
23.矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,
(1)求AB;
(2)求AD;
(3)求矩形ABCD的面积.
【考点】矩形的性质.
【分析】(1)由矩形ABCD中,∠AOB=60°,易得△AOB是等边三角形,又由AC=10,则可求得OA的长,继而求得答案;
(2)在Rt△ABD中,直接利用勾股定理求解即可求得答案;
(3)由S矩形ABCD=AD AB,即可求得答案.
【解答】解:(1)∵矩形ABCD中,AC=10,
∴OA=AC=5,BD=AC=10,
∴OB=BD=5,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=5;
(2)∵∠BAD=90°,
∴AD===5;
(3)S矩形ABCD=AD AB=25.
24.如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
【考点】平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
【分析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
【解答】证明:(1)在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=.
又∵CE=BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(2)解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=CD=2,DH=2.
在 CEDF中,CE=DF=AD=3,则EH=1.
∴在Rt△DHE中,根据勾股定理知DE==.
25.台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由A行驶向B,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20千米/小时,台风影响该海港持续的时间有多长?
【考点】勾股定理的应用.
【分析】(1)利用勾股定理的逆定理得出△ABC是直角三角形,进而利用三角形面积得出CD的长,进而得出海港C是否受台风影响;
(2)利用勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间.
【解答】解:(1)海港C受台风影响,
理由:过点C作CD⊥AB,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km,
∵台风的速度为20千米/小时,
∴140÷20=7(小时),
答:台风影响该海港持续的时间为7小时.
26.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 平行四边形 ,并证明你的结论.
(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足 AC⊥BD 条件时,四边形EFGH是矩形;并证明你的结论.
(3)连接四边形ABCD的对角线AC与BD,当AC与BD满足条件 AC⊥BD且AC=BD 时,四边形EFGH是正方形.(不用证明)
【考点】中点四边形.
【分析】(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=BD,FG∥BD,FG═BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)根据邻边相等的矩形为正方形进行解答.
【解答】解:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD.
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=BD,
同理FG∥BD,FG=BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
故答案是:平行四边形;
(2)当AC⊥BD时,四边形EFGH是矩形.理由如下:
如图,连结AC.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案是:AC⊥BD;
(3)当AC⊥BD且AC=BD时,四边形EFGH是正方形.
故答案是:AC⊥BD且AC=BD.
2017年3月3日
同课章节目录
