第17章 函数及其图象 单元测试卷
文档属性
| 名称 | 第17章 函数及其图象 单元测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 524.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-04 23:10:37 | ||
图片预览



文档简介
第17章 函数及其图象 单元测试卷
一、选择题(每题2分,共20分)
1.函数y=+x-2的自变量x的取值范围是( )
A.x≥2 B.x>2
C.x≠2 D.x≤2
2.若反比例函数y=(k≠0)的图象经过点P(-2,3),则该函数的图象不经过的点是( )
A.(3,-2) B.(1,-6)
C.(-1,6) D.(-1,-6)
3.函数y1=3x+b与y2=ax+b的图象如图所示,当y1,y2的值都大于零时,x的取值范围是( )21教育网
A.x>-1 B.x>0
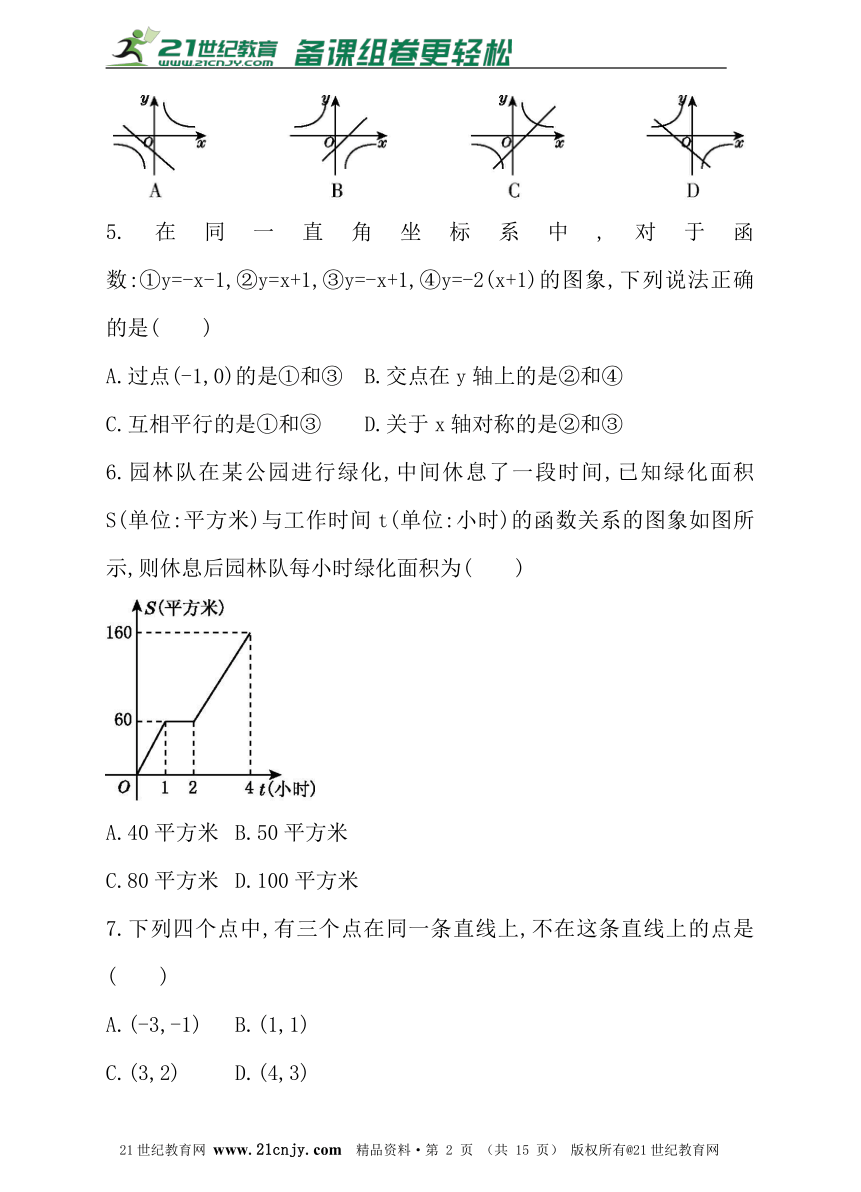
C.04. 在同一平面直角坐标系中,函数y=x-1与函数y=的图象可能是( )
5.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )21·cn·jy·com
A.过点(-1,0)的是①和③ B.交点在y轴上的是②和④
C.互相平行的是①和③ D.关于x轴对称的是②和③
6.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.40平方米 B.50平方米
C.80平方米 D.100平方米
7.下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
A.(-3,-1) B.(1,1)
C.(3,2) D.(4,3)
8.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①f(a,b)=(-a,b),如:f(1,3)=(-1,3);②g(a,b)=(b,a),如:g(1,3)=(3,1);③h(a,b)=(-a,-b),如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),那么f(h(5,-3))等于( )
A.(-5,-3) B.(5,3)
C.(5,-3) D.(-5,3)
9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2xA.x< B.x<3 C.x> D.x>3
10.如图,反比例函数y=(x>0)的图象经过长方形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为9,则k的值为( )
A.1 B.2 C.3 D.4
二、填空题(每题2分,共20分)
11.一次函数y=2x-6的图象与x轴的交点坐标为_____________.?
12.设点M(1,2)关于原点的对称点为M',则点M'的坐标为_____________.?
13.在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第_____________象限.?21世纪教育网版权所有
14.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x115.当m=_____________时,函数y=(2m-1)x|3m-2|+3是一次函数,且y随x的增大而增大.?21·世纪*教育网
16.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连结OA,OB,已知△OAB的面积为2,则k1-k2=_____________.
?
17.根据指令[s,α](s≥0,0°≤α≤360°),机器人在平面上能完成如下动作:先在原地顺时针旋转角度α,再朝其面对的方向沿直线行走距离s,现在机器人在平面直角坐标系的原点,且面对y轴负方向,若指令是[4,180°],则完成指令后机器人所处的位置是_____________.?
18.已知一次函数的图象经过点(-1,2)和(-3,4),则这个一次函数的关系式为_____________.?
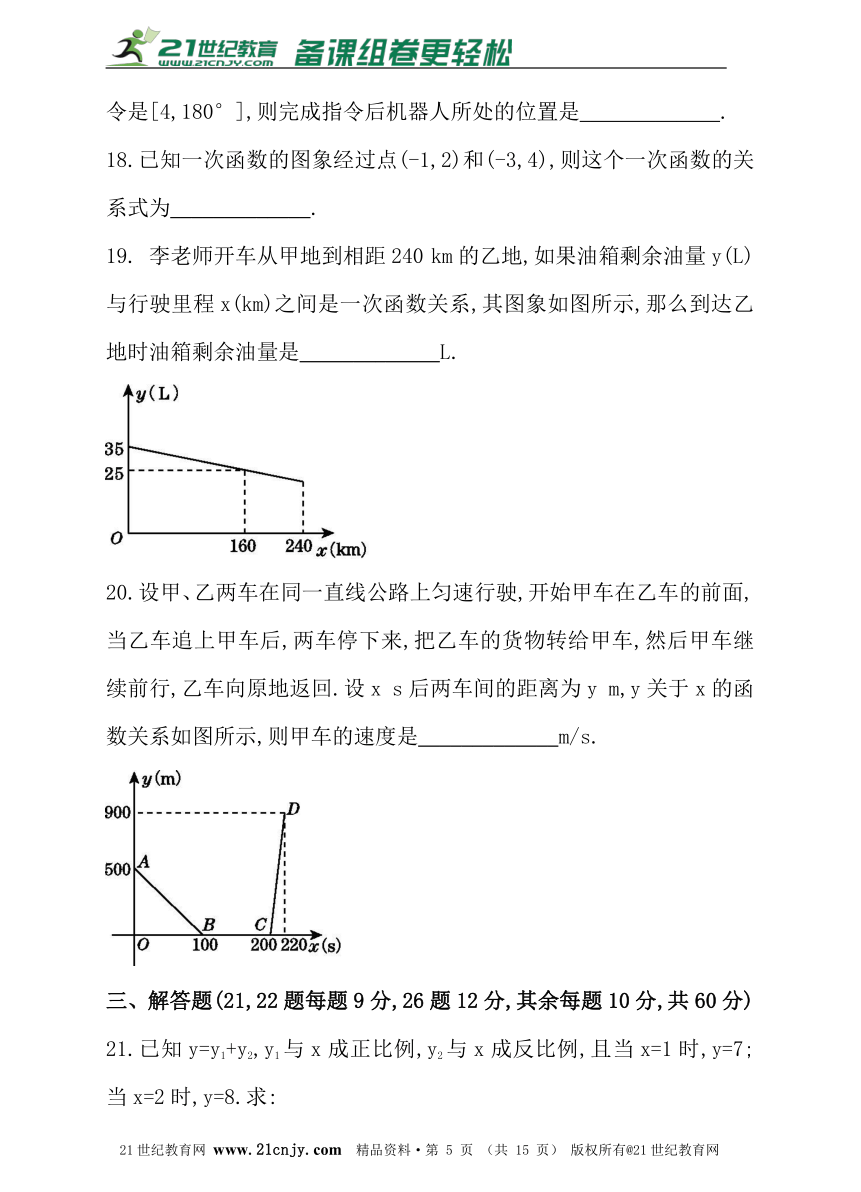
19. 李老师开车从甲地到相距240 km的乙地,如果油箱剩余油量y(L)与行驶里程x(km)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是_____________L.
20.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x s后两车间的距离为y m,y关于x的函数关系如图所示,则甲车的速度是_____________m/s.
三、解答题(21,22题每题9分,26题12分,其余每题10分,共60分)
21.已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=7;当x=2时,y=8.求:
(1)y与x之间的函数关系式;
(2)自变量的取值范围;
(3)当x=4时,y的值.
22.已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),如图所示.【来源:21cnj*y.co*m】
(1)求这两个函数的关系式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
23.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元,3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案.
24.如图所示,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=,且点B的横坐标是其纵坐标的2倍.
(1)求反比例函数的关系式;
(2)设点A的横坐标为m,△ABO的面积为S,求S与m之间的函数关系式,并求出自变量的取值范围.
25.1号探测气球从海拔5 m处出发,以1 m/min的速度上升,与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升.两个气球都匀速上升了50 min.
设气球上升时间为x min(0≤x≤50).
(1)根据题意,填写下表.
上升时间(min)
10
30
…
x
1号探测气球所在位置的海拔(m)
15
…
2号探测气球所在位置的海拔(m)
30
…
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.21*cnjy*com
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
26.2016年3月27日“丽水半程马拉松竞赛”在丽水举行,某运动员从起点万地广场西门出发,途经紫金大
桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程s(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:21*cnjy*com
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线对应的函数关系式;
②该运动员跑完赛程用时多少分钟?
参考答案
一、1.【答案】B 2.【答案】D 3.【答案】D
4.【答案】C 5.【答案】C 6.【答案】B
7.【答案】D
解:设这条直线对应的函数关系式为y=kx+b.把点(-3,-1),(1,1)的坐标分别代入一次函数的关系式y=kx+b中,得-3k+b=-1,k+b=1,解得k=0.5,b=0.5,∴y=0.5x+0.5.当x=3时,y=2,∴点(3,2)在直线y=0.5x+0.5上,当x=4时,y=2.5,∴点(4,3)不在直线y=0.5x+0.5上.
8.【答案】B
解:按照本题的规定可知:h(5,-3)=(-5,3),f(-5,3)=(5,3).所以f(h(5,-3))=(5,3).www-2-1-cnjy-com
9.【答案】A
10.【答案】C
解:由题意得,E,M,D位于反比例函数的图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S长方形ONMG=|k|,又∵M为长方形ABCO对角线的交点,∴S长方形ABCO=4S长方形ONMG=4|k|,由于函数图象在第一象限,k>0,则S四边形ODBE=S长方形ABCO-S△OCE-S△OAD,即9=4k-2·,解得k=3.故选C.2·1·c·n·j·y
二、11.【答案】 (3,0)
12.【答案】(-1,-2)
13.【答案】四
解:∵在一次函数y=kx+2中,y随x的增大而增大,∴k>0,∵2>0,∴此函数的图象经过第一、二、三象限,不经过第四象限.
14.【答案】>
解:当k>0时,反比例函数图象的两个分支分别在第一、三象限内,且在每个象限内,y随x的增大而减小;当k<0时,反比例函数图象的两个分支分别在第二、四象限内,且在每个象限内,y随x的增大而增大.本题中,k=2>0,x1y2.21教育名师原创作品
15.【答案】1
解:由题意知
解得∴m=1.
16.【答案】4
解:k的几何意义是:在反比例函数y=的图象上任意取一点(x,y),从这一点分别向x轴,y轴作垂线,与x轴,y轴所围成的四边形的面积等于|k|.由△ABO的面积为2,可知S△AOP-S△BOP=2,即|k1|-|k2|=k1-k2=(k1-k2)=2,解得k1-k2=4.【出处:21教育名师】
17.【答案】(0,4)
解:∵指令为[4,180°],∴机器人应顺时针旋转180°,再向面对的方向走4个单位长度.∵机器人在平面直角坐标系的坐标原点,且面对y轴负方向,∴机器人旋转后将面对y轴正方向,向y轴正半轴走4个单位长度,∴机器人所处的位置是(0,4).
18.【答案】y=-x+1
19.【答案】20
解:设函数关系式为y=kx+b,∵点(0,35),(160,25)在该函数的图象上,
∴解得
∴函数关系式为y=-x+35.
∴当x=240时,y=-×240+35=20,即到达乙地时油箱剩余油量是20 L.
20.【答案】20
解:设甲车的速度为v m/s,乙车的速度为u m/s,由图象可得方程组解得v=20.
三、21.解:(1)∵y1与x成正比例,∴设y1=k1x(k1≠0),∵y2与x成反比例,∴设y2=(k2≠0),∴y=y1+y2=k1x+(k1≠0,k2≠0).
把与分别代入上式,得
解得
∴y与x的函数关系式为y=3x+.
(2)自变量的取值范围是x≠0.
(3)当x=4时,y=3x+=3×4+=13.
22.解:(1)∵函数y1=的图象过点A(1,4),∴4=,∴k=4,即y1=,又∵点B(m,-2)在y1=的图象上,∴m=-2,∴B(-2,-2),又∵一次函数y2=ax+b的图象过A,B两点,www.21-cn-jy.com
∴解之得
∴y2=2x+2.
综上可得y1=,y2=2x+2.
(2)0(3)过B作BD⊥AC于点D,由图象及题意可得:AC=8,BD=3,∴S△ABC=AC·BD= ×8×3=12.2-1-c-n-j-y
23.解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元.
由题意得解得
∴一只A型节能灯的售价是5元,一只B型节能灯的售价是7元.
(2)设购进A型节能灯m只,总费用为W元,则
W=5m+7×(50-m)=-2m+350.
∵k=-2<0,∴W随m的增大而减小,
当m取最大值时,W最小.
又m≤3(50-m),∴m≤37.5.
又m为正整数,∴当m=37时,W的值最小.
50-37=13(只).
∴最省钱的购买方案是购进37只A型节能灯,13只B型节能灯.
24.解:(1)设点B的坐标为(2t,t),且t<0.由题意得(2t)2+t2=()2,解得t=-1(正值舍去).所以点B的坐标为(-2,-1).设反比例函数的关系式为y=(k1≠0),把点(-2,-1)的坐标代入,求得k1=2.故反比例函数的关系式为y=.【版权所有:21教育】
(2)由一次函数y=kx+b的图象经过点A,B(-2,-1),得
解得(m≠-2).所以一次函数的关系式为
y=x+(m≠-2).故点D的坐标为(m-2,0),则S=S△BDO+S△ADO=|m-2|×|-1|+|m-2|×.因为k>0,b>0,所以有解得025.解:(1)35;x+5;20;0.5x+15
(2)在某时刻两个气球能位于同一高度.
根据题意,得x+5=0.5x+15,解得x=20.
有x+5=25.
答:此时,气球上升了20 min,都位于海拔25 m的高度.
(3)当30≤x≤50时,
由题意,可知1号气球所在位置的海拔始终高于2号气球所在位置的海拔,设两个气球在同一时刻所在位置的海拔相差y m.
则y=(x+5)-(0.5x+15)=0.5x-10.
∵0.5>0,
∴y随x的增大而增大.
∴当x=50时,y取得最大值15.
答:当30≤x≤50时,两个气球所在位置的海拔最多相差15 m.
26.解:(1)∵从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,
∴a=0.3×35=10.5.
(2)①由线段OA经过点O(0,0),A(35,10.5),
易知线段OA对应的函数关系式为s=0.3t(0≤t≤35).
当s=2.1时,0.3t=2.1,解得t=7.
∵该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟,
∴该运动员从起点到第二次经过C点所用的时间是7+68=75(分钟),
∴直线AB经过点(35,10.5),(75,2.1),
设直线AB对应的函数关系式为s=kt+b,
∴解得
∴直线AB对应的函数关系式为s=-0.21t+17.85.
②对于s=-0.21t+17.85,令s=0,则-0.21t+17.85=0,解得t=85.
∴该运动员跑完赛程用时85分钟.
一、选择题(每题2分,共20分)
1.函数y=+x-2的自变量x的取值范围是( )
A.x≥2 B.x>2
C.x≠2 D.x≤2
2.若反比例函数y=(k≠0)的图象经过点P(-2,3),则该函数的图象不经过的点是( )
A.(3,-2) B.(1,-6)
C.(-1,6) D.(-1,-6)
3.函数y1=3x+b与y2=ax+b的图象如图所示,当y1,y2的值都大于零时,x的取值范围是( )21教育网
A.x>-1 B.x>0
C.0
5.在同一直角坐标系中,对于函数:①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是( )21·cn·jy·com
A.过点(-1,0)的是①和③ B.交点在y轴上的是②和④
C.互相平行的是①和③ D.关于x轴对称的是②和③
6.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A.40平方米 B.50平方米
C.80平方米 D.100平方米
7.下列四个点中,有三个点在同一条直线上,不在这条直线上的点是( )
A.(-3,-1) B.(1,1)
C.(3,2) D.(4,3)
8.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①f(a,b)=(-a,b),如:f(1,3)=(-1,3);②g(a,b)=(b,a),如:g(1,3)=(3,1);③h(a,b)=(-a,-b),如:h(1,3)=(-1,-3).
按照以上变换有:f(g(2,-3))=f(-3,2)=(3,2),那么f(h(5,-3))等于( )
A.(-5,-3) B.(5,3)
C.(5,-3) D.(-5,3)
9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x
10.如图,反比例函数y=(x>0)的图象经过长方形OABC对角线的交点M,分别与AB,BC交于点D,E,若四边形ODBE的面积为9,则k的值为( )
A.1 B.2 C.3 D.4
二、填空题(每题2分,共20分)
11.一次函数y=2x-6的图象与x轴的交点坐标为_____________.?
12.设点M(1,2)关于原点的对称点为M',则点M'的坐标为_____________.?
13.在一次函数y=kx+2中,若y随x的增大而增大,则它的图象不经过第_____________象限.?21世纪教育网版权所有
14.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1
16.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连结OA,OB,已知△OAB的面积为2,则k1-k2=_____________.
?
17.根据指令[s,α](s≥0,0°≤α≤360°),机器人在平面上能完成如下动作:先在原地顺时针旋转角度α,再朝其面对的方向沿直线行走距离s,现在机器人在平面直角坐标系的原点,且面对y轴负方向,若指令是[4,180°],则完成指令后机器人所处的位置是_____________.?
18.已知一次函数的图象经过点(-1,2)和(-3,4),则这个一次函数的关系式为_____________.?
19. 李老师开车从甲地到相距240 km的乙地,如果油箱剩余油量y(L)与行驶里程x(km)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是_____________L.
20.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x s后两车间的距离为y m,y关于x的函数关系如图所示,则甲车的速度是_____________m/s.
三、解答题(21,22题每题9分,26题12分,其余每题10分,共60分)
21.已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=7;当x=2时,y=8.求:
(1)y与x之间的函数关系式;
(2)自变量的取值范围;
(3)当x=4时,y的值.
22.已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),如图所示.【来源:21cnj*y.co*m】
(1)求这两个函数的关系式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
23.学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元,3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案.
24.如图所示,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=,且点B的横坐标是其纵坐标的2倍.
(1)求反比例函数的关系式;
(2)设点A的横坐标为m,△ABO的面积为S,求S与m之间的函数关系式,并求出自变量的取值范围.
25.1号探测气球从海拔5 m处出发,以1 m/min的速度上升,与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升.两个气球都匀速上升了50 min.
设气球上升时间为x min(0≤x≤50).
(1)根据题意,填写下表.
上升时间(min)
10
30
…
x
1号探测气球所在位置的海拔(m)
15
…
2号探测气球所在位置的海拔(m)
30
…
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.21*cnjy*com
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
26.2016年3月27日“丽水半程马拉松竞赛”在丽水举行,某运动员从起点万地广场西门出发,途经紫金大
桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程s(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:21*cnjy*com
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线对应的函数关系式;
②该运动员跑完赛程用时多少分钟?
参考答案
一、1.【答案】B 2.【答案】D 3.【答案】D
4.【答案】C 5.【答案】C 6.【答案】B
7.【答案】D
解:设这条直线对应的函数关系式为y=kx+b.把点(-3,-1),(1,1)的坐标分别代入一次函数的关系式y=kx+b中,得-3k+b=-1,k+b=1,解得k=0.5,b=0.5,∴y=0.5x+0.5.当x=3时,y=2,∴点(3,2)在直线y=0.5x+0.5上,当x=4时,y=2.5,∴点(4,3)不在直线y=0.5x+0.5上.
8.【答案】B
解:按照本题的规定可知:h(5,-3)=(-5,3),f(-5,3)=(5,3).所以f(h(5,-3))=(5,3).www-2-1-cnjy-com
9.【答案】A
10.【答案】C
解:由题意得,E,M,D位于反比例函数的图象上,则S△OCE=,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S长方形ONMG=|k|,又∵M为长方形ABCO对角线的交点,∴S长方形ABCO=4S长方形ONMG=4|k|,由于函数图象在第一象限,k>0,则S四边形ODBE=S长方形ABCO-S△OCE-S△OAD,即9=4k-2·,解得k=3.故选C.2·1·c·n·j·y
二、11.【答案】 (3,0)
12.【答案】(-1,-2)
13.【答案】四
解:∵在一次函数y=kx+2中,y随x的增大而增大,∴k>0,∵2>0,∴此函数的图象经过第一、二、三象限,不经过第四象限.
14.【答案】>
解:当k>0时,反比例函数图象的两个分支分别在第一、三象限内,且在每个象限内,y随x的增大而减小;当k<0时,反比例函数图象的两个分支分别在第二、四象限内,且在每个象限内,y随x的增大而增大.本题中,k=2>0,x1
15.【答案】1
解:由题意知
解得∴m=1.
16.【答案】4
解:k的几何意义是:在反比例函数y=的图象上任意取一点(x,y),从这一点分别向x轴,y轴作垂线,与x轴,y轴所围成的四边形的面积等于|k|.由△ABO的面积为2,可知S△AOP-S△BOP=2,即|k1|-|k2|=k1-k2=(k1-k2)=2,解得k1-k2=4.【出处:21教育名师】
17.【答案】(0,4)
解:∵指令为[4,180°],∴机器人应顺时针旋转180°,再向面对的方向走4个单位长度.∵机器人在平面直角坐标系的坐标原点,且面对y轴负方向,∴机器人旋转后将面对y轴正方向,向y轴正半轴走4个单位长度,∴机器人所处的位置是(0,4).
18.【答案】y=-x+1
19.【答案】20
解:设函数关系式为y=kx+b,∵点(0,35),(160,25)在该函数的图象上,
∴解得
∴函数关系式为y=-x+35.
∴当x=240时,y=-×240+35=20,即到达乙地时油箱剩余油量是20 L.
20.【答案】20
解:设甲车的速度为v m/s,乙车的速度为u m/s,由图象可得方程组解得v=20.
三、21.解:(1)∵y1与x成正比例,∴设y1=k1x(k1≠0),∵y2与x成反比例,∴设y2=(k2≠0),∴y=y1+y2=k1x+(k1≠0,k2≠0).
把与分别代入上式,得
解得
∴y与x的函数关系式为y=3x+.
(2)自变量的取值范围是x≠0.
(3)当x=4时,y=3x+=3×4+=13.
22.解:(1)∵函数y1=的图象过点A(1,4),∴4=,∴k=4,即y1=,又∵点B(m,-2)在y1=的图象上,∴m=-2,∴B(-2,-2),又∵一次函数y2=ax+b的图象过A,B两点,www.21-cn-jy.com
∴解之得
∴y2=2x+2.
综上可得y1=,y2=2x+2.
(2)0
23.解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元.
由题意得解得
∴一只A型节能灯的售价是5元,一只B型节能灯的售价是7元.
(2)设购进A型节能灯m只,总费用为W元,则
W=5m+7×(50-m)=-2m+350.
∵k=-2<0,∴W随m的增大而减小,
当m取最大值时,W最小.
又m≤3(50-m),∴m≤37.5.
又m为正整数,∴当m=37时,W的值最小.
50-37=13(只).
∴最省钱的购买方案是购进37只A型节能灯,13只B型节能灯.
24.解:(1)设点B的坐标为(2t,t),且t<0.由题意得(2t)2+t2=()2,解得t=-1(正值舍去).所以点B的坐标为(-2,-1).设反比例函数的关系式为y=(k1≠0),把点(-2,-1)的坐标代入,求得k1=2.故反比例函数的关系式为y=.【版权所有:21教育】
(2)由一次函数y=kx+b的图象经过点A,B(-2,-1),得
解得(m≠-2).所以一次函数的关系式为
y=x+(m≠-2).故点D的坐标为(m-2,0),则S=S△BDO+S△ADO=|m-2|×|-1|+|m-2|×.因为k>0,b>0,所以有解得0
(2)在某时刻两个气球能位于同一高度.
根据题意,得x+5=0.5x+15,解得x=20.
有x+5=25.
答:此时,气球上升了20 min,都位于海拔25 m的高度.
(3)当30≤x≤50时,
由题意,可知1号气球所在位置的海拔始终高于2号气球所在位置的海拔,设两个气球在同一时刻所在位置的海拔相差y m.
则y=(x+5)-(0.5x+15)=0.5x-10.
∵0.5>0,
∴y随x的增大而增大.
∴当x=50时,y取得最大值15.
答:当30≤x≤50时,两个气球所在位置的海拔最多相差15 m.
26.解:(1)∵从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,
∴a=0.3×35=10.5.
(2)①由线段OA经过点O(0,0),A(35,10.5),
易知线段OA对应的函数关系式为s=0.3t(0≤t≤35).
当s=2.1时,0.3t=2.1,解得t=7.
∵该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟,
∴该运动员从起点到第二次经过C点所用的时间是7+68=75(分钟),
∴直线AB经过点(35,10.5),(75,2.1),
设直线AB对应的函数关系式为s=kt+b,
∴解得
∴直线AB对应的函数关系式为s=-0.21t+17.85.
②对于s=-0.21t+17.85,令s=0,则-0.21t+17.85=0,解得t=85.
∴该运动员跑完赛程用时85分钟.
