第18章 平行四边形 单元测试卷
图片预览
文档简介
第18章 平行四边形 单元测试卷
一、选择题(每题3分,共30分)
1.在?ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A.1∶2∶3∶4 B.1∶2∶1∶2
C.1∶1∶2∶2 D.1∶2∶2∶1
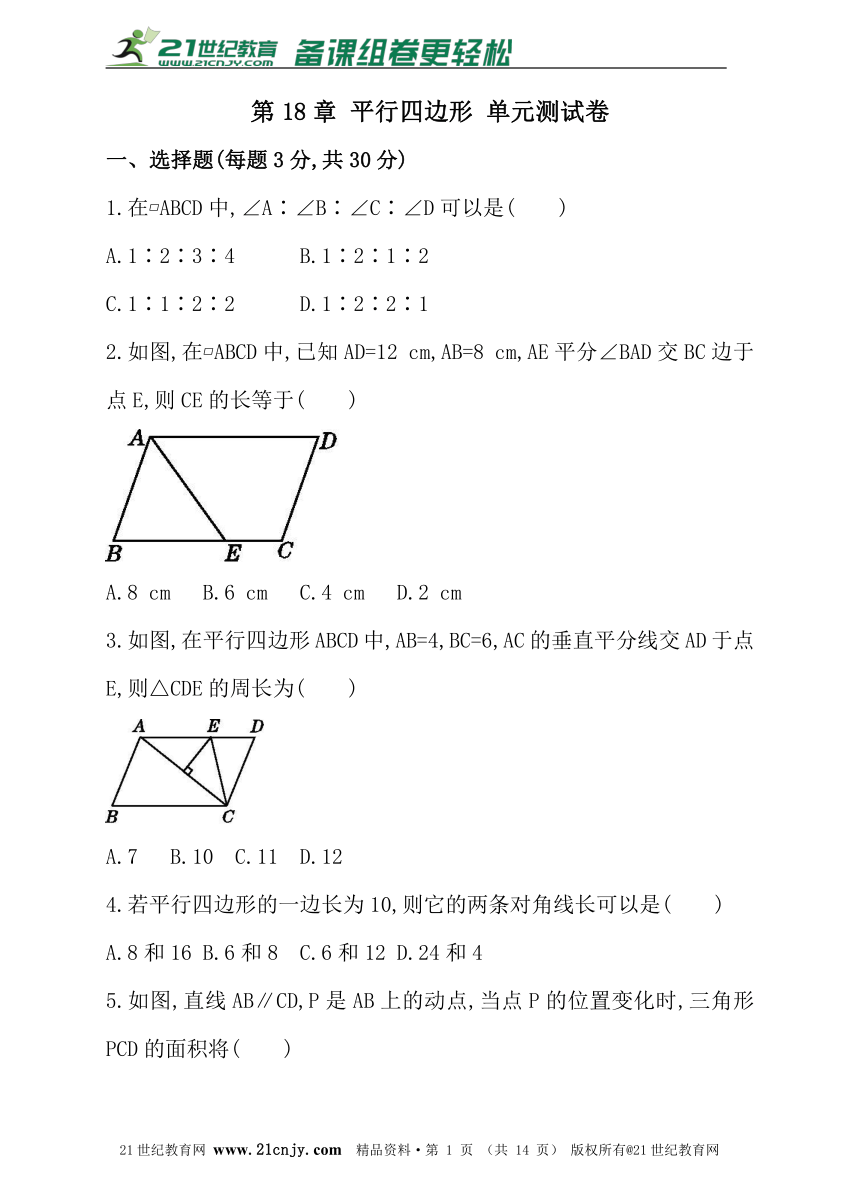
2.如图,在?ABCD中,已知AD=12 cm,AB=8 cm,AE平分∠BAD交BC边于点E,则CE的长等于( )【来源:21cnj*y.co*m】
A.8 cm B.6 cm C.4 cm D.2 cm
3.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长为( )
A.7 B.10 C.11 D.12
4.若平行四边形的一边长为10,则它的两条对角线长可以是( )
A.8和16 B.6和8 C.6和12 D.24和4
5.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大 B.变小
C.不变 D.变大变小要看点P向左还是向右移动
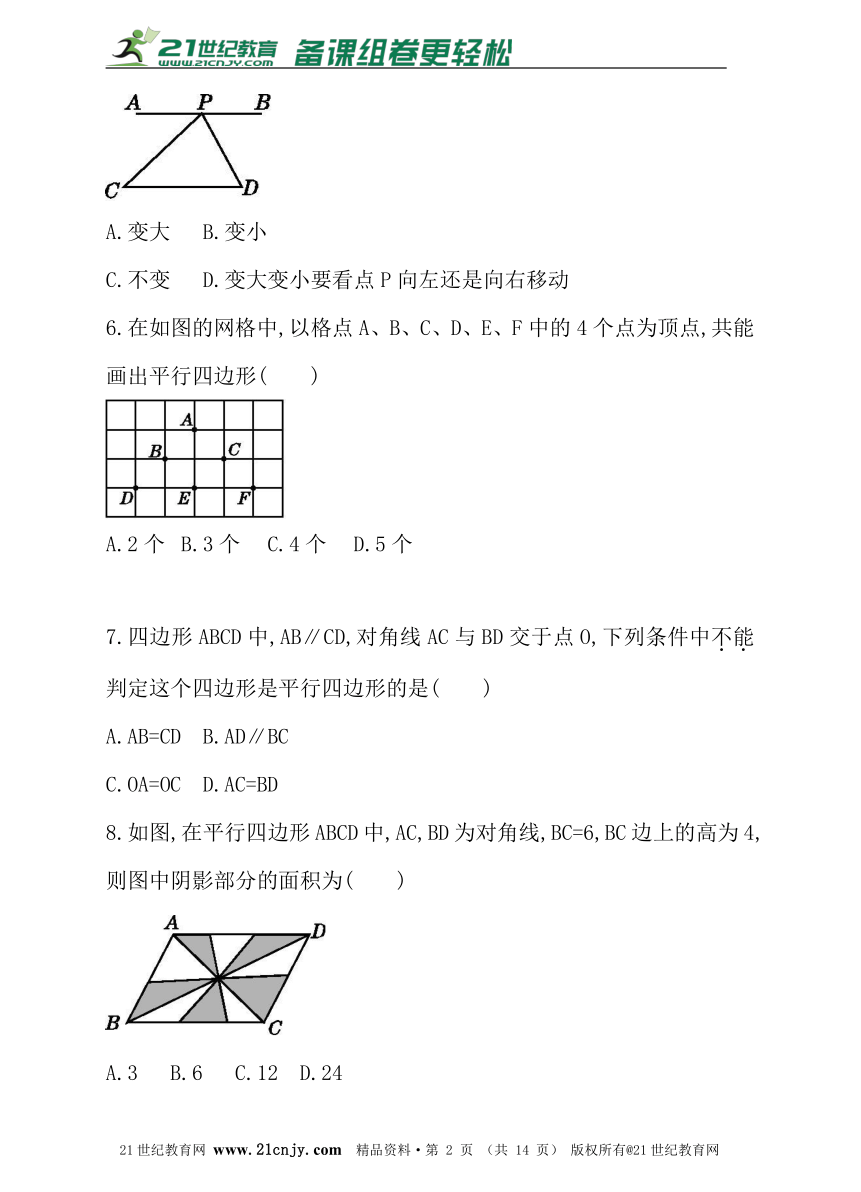
6.在如图的网格中,以格点A、B、C、D、E、F中的4个点为顶点,共能画出平行四边形( )
A.2个 B.3个 C.4个 D.5个
7.四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能判定这个四边形是平行四边形的是( )21教育名师原创作品
A.AB=CD B.AD∥BC
C.OA=OC D.AC=BD
8.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
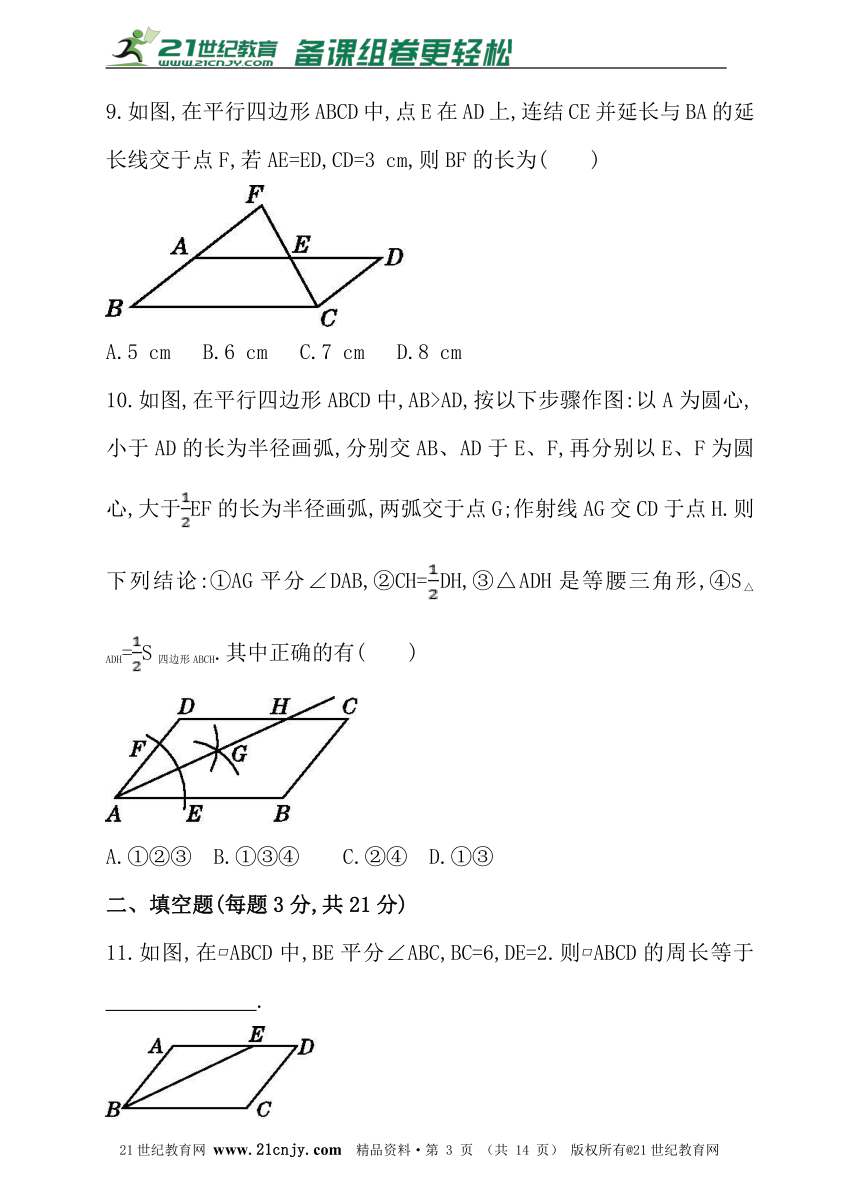
9.如图,在平行四边形ABCD中,点E在AD上,连结CE并延长与BA的延长线交于点F,若AE=ED,CD=3 cm,则BF的长为( )
A.5 cm B.6 cm C.7 cm D.8 cm
10.如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、AD于E、F,再分别以E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=DH,③△ADH是等腰三角形,④S△ADH=S四边形ABCH.其中正确的有( )21世纪教育网版权所有
A.①②③ B.①③④ C.②④ D.①③
二、填空题(每题3分,共21分)
11.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2.则?ABCD的周长等于______________.21·cn·jy·com
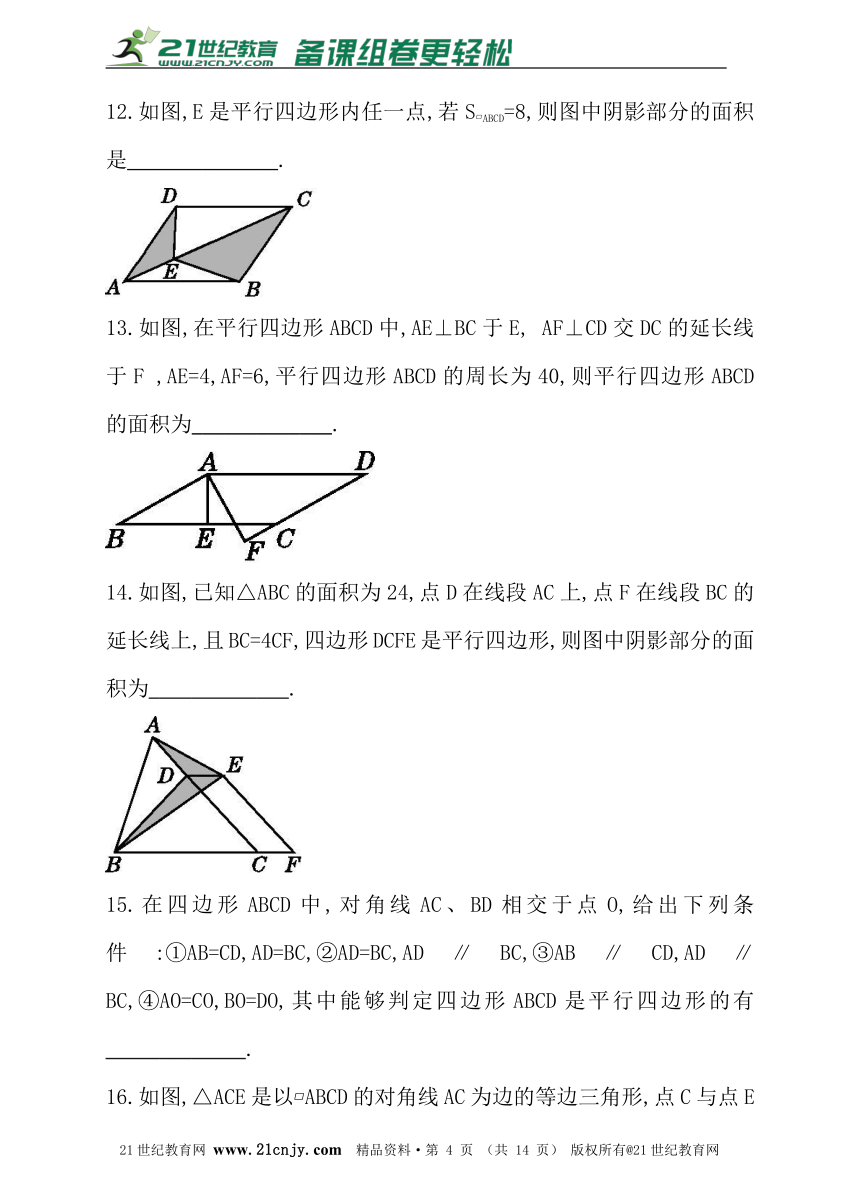
12.如图,E是平行四边形内任一点,若S?ABCD=8,则图中阴影部分的面积是______________.
13.如图,在平行四边形ABCD中,AE⊥BC于E, AF⊥CD交DC的延长线于F ,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为_____________.
14.如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为_____________.?
15.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=BC,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO,其中能够判定四边形ABCD是平行四边形的有_____________.?21教育网
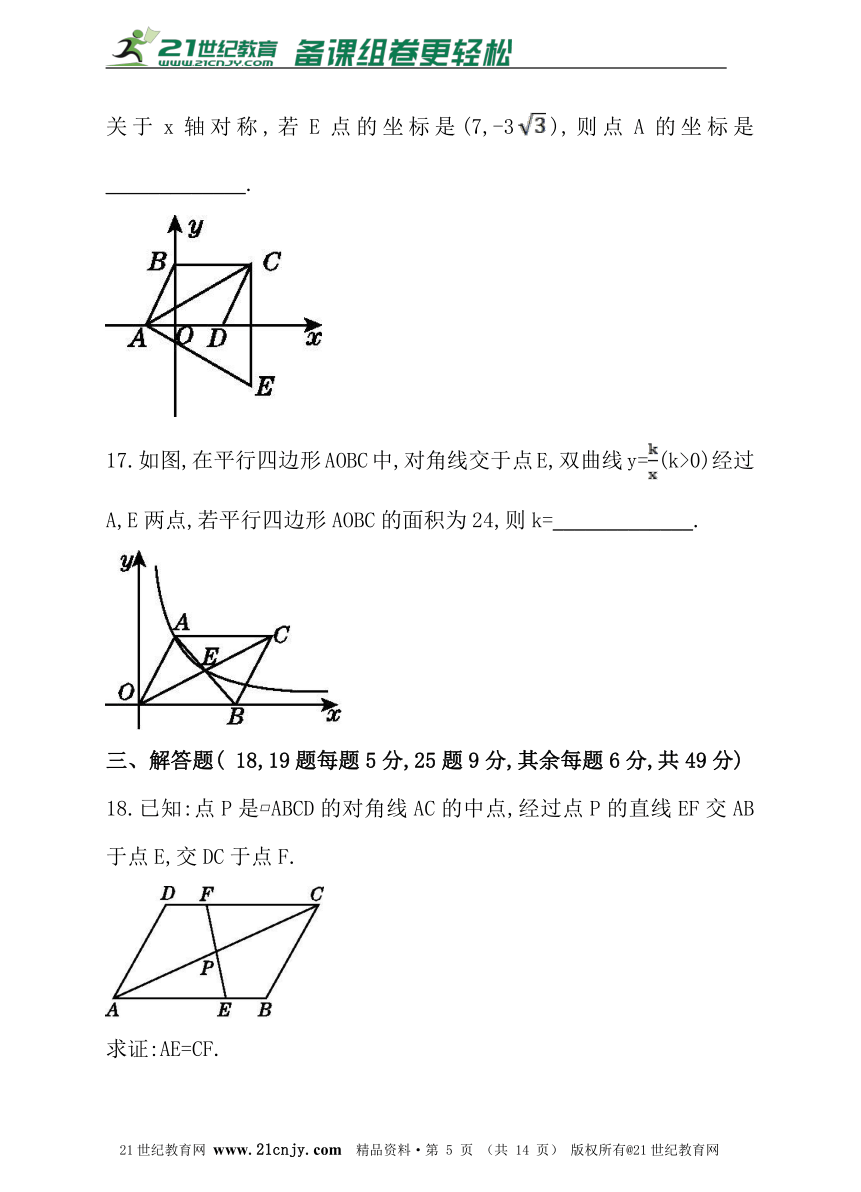
16.如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称,若E点的坐标是(7,-3),则点A的坐标是_____________.
17.如图,在平行四边形AOBC中,对角线交于点E,双曲线y=(k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k=_____________.
三、解答题( 18,19题每题5分,25题9分,其余每题6分,共49分)
18.已知:点P是?ABCD的对角线AC的中点,经过点P的直线EF交AB于点E,交DC于点F.
求证:AE=CF.
19.如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,连结DE、BF.
(1)写出图中所有的全等三角形.
(2)求证:DE∥BF.
20.如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
21.如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE≌△DFE;
(2)连结BD、AF,试判断四边形ABDF的形状,并证明你的结论.
22.已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.
求证:四边形ABOE、四边形DCOE都是平行四边形.
23.如图,在四边形ABCD中,∠ADB=∠CBD=90°,BE∥CD交AD于E,且EA=EB.若AB=4,DB=4.www.21-cn-jy.com
求四边形ABCD的面积.
24.如图①,已知在△ABC中,AB=AC,点P为底边BC上(端点B、C除外)任意一点,且PE∥AC交AB于E,PF∥AB交AC于F.【来源:21·世纪·教育·网】
(1)试问线段PE、PF、AB之间有什么数量关系,并说明理由.
(2)如图②,将“点P为底边BC上任意一点”改为“点P为底边BC延长线上任意一点”,其他条件不变,上述结论还成立吗?如果不成立,你能得到什么结论?请说明你的理由.21·世纪*教育网
25.如图,在平行四边形ABCD中,AB=2 cm,BC=12 cm,∠B=45°,点P在边BC上,由点B向点C运动,速度为每秒2 cm,点Q在边AD上,与点P同时出发,由点D向点A运动,速度为每秒1 cm,连结PQ,设运动时间为t s.2·1·c·n·j·y
(1)当t为何值时,四边形ABPQ为平行四边形?
(2)设四边形ABPQ的面积为y cm2,请用含有t的代数式表示y;
(3)当点P运动至何处时,四边形ABPQ的面积是?ABCD面积的四分之三?
参考答案
一、1.【答案】B
解:由于平行四边形对角相等,所以对角的比数应该相等,其中A,C,D都不满足,只有B满足.故选B.
2.【答案】C
3.【答案】B
解:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
4.【答案】A
解:在?ABCD中,AD=10,对角线相交于O点,根据平行四边形的性质推出OA=OC=AC,OB=OD=BD,求出每个选项中OA和OD的长度,看看线段OA、OD、AD是否能围成三角形(即是否符合三角形的三边关系)即可.
5.【答案】C
解:设平行线AB、CD间的距离为h,则S△PCD=CD·h.∵CD的长度不变,h的大小不变,∴三角形PCD的面积不变.故选C.www-2-1-cnjy-com
6.【答案】B
解:观察题图可知,有?ABEC,?BDEC,?BEFC共3个.故选B.
7.【答案】D 8.【答案】C 9.【答案】B
10.【答案】D
二、11.【答案】20
解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC.∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE.∵AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴?ABCD的周长=4+4+6+6=20,故答案为20.21cnjy.com
12.【答案】4
13.【答案】48
解:设BC=x,则CD=20-x,根据“等面积法”得4x=6(20-x),解得x=12,∴BC=12,∴平行四边形ABCD的面积为AE·BC=4×12=48.
14.【答案】6
解:∵四边形DCFE是平行四边形,∴DE=CF,DE∥CF,∴△DEB的面积为四边形DCFE面积的一半.∵BC=4CF,∴DE=BC.设△ABC中BC边上的高为h,则S△ADE+S△DEB=DE·h=·BC·h=×24=6.21*cnjy*com
15.【答案】①②③④ 16.【答案】(-2,0)
17.【答案】8
解:设A(x,),B(a,0),过点A作AD⊥OB于点D,过点E作EF⊥OB于点F,如图,
由平行四边形的性质可知AE=EB,
∴E.
∵点E在双曲线上,∴·=k,∴a=3x.∵平行四边形的面积是24,∴a·=3x·=3k=24,∴k=8.【版权所有:21教育】
三、18.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠DCA=∠BAC.
又∵点P是AC的中点,∴AP=CP.
在△FCP和△EAP中,
∴△FCP≌△EAP,
∴AE=CF.
19.(1)解:△AED≌△CFB,△ABF≌△CDE,△ABC≌△CDA.
(2)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC.∴∠DAC=∠BCA,
在△ADE和△CBF中,
∴△ADE≌△CBF.∴∠AED=∠CFB.
∴∠DEC=∠AFB.∴DE∥BF.
20.解:(1)∵四边形ABCD是平行四边形,∴AD∥CB,∴∠DAB+∠CBA=180°.又∵AP和BP分别平分∠DAB和∠CBA,∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,∴在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°.
(2)∵AP平分∠DAB且AB∥CD,∴∠DAP=∠PAB=∠DPA,∴△ADP是等腰三角形,∴DP=AD=5 cm.同理可得PC=CB=5 cm,即AB=DC=DP+PC=10 cm.在Rt△APB中,∵∠APB=90°,AB=10 cm,AP=8 cm,∴BP==6(cm),∴△APB的周长为AB+AP+BP=10+8+6=24(cm). 2-1-c-n-j-y
21.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CF,∴∠BAD=∠ADF,∠ABE=∠DFE.∵E是AD的中点,∴AE=DE,∴△ABE≌△DFE.
(2)解:如图,四边形ABDF是平行四边形.
证明:∵△ABE≌△DFE,∴AB=DF.又∵AB∥DF,
∴四边形ABDF是平行四边形.
22.证明:∵在?ABCD中,对角线AC交BD于点O,∴OB=OD.又∵四边形AODE是平行四边形,∴AE∥OD且AE=OD,∴AE∥OB且AE=OB,∴四边形ABOE是平行四边形,∴AB∥OE,且AB=OE.又∵在?ABCD中,AB∥CD,AB=CD,∴OE∥CD,OE=CD,∴四边形DCOE也是平行四边形.
23.解:∵∠ADB=∠CBD=90°,∴DE∥CB.∵BE∥CD,∴四边形BEDC是平行四边形,∴BC=DE.在Rt△ABD中,由勾股定理得AD===8.设DE=x,则EA=8-x,∴EB=EA=8-x.在Rt△BDE中,由勾股定理得 DE2+DB2=EB2,∴x2+42=(8-x)2.解得x=3.∴BC=DE=3,∴S四边形ABCD=S△ABD+S△BDC=AD·DB+DB·BC=16+6=22.
24.解:(1)PE+PF=AB.理由:∵PE∥AC,PF∥AB,∴四边形AEPF是平行四边形,∴AE=PF.∵PE∥AC,∴∠EPB=∠C.又∵AB=AC,∴∠B=∠C=∠EPB,∴BE=PE,∴PE+PF=AB.【出处:21教育名师】
(2)不成立,结论为PE=PF+AB.理由:∵PE∥AC,PF∥AB,∴四边形AFPE是平行四边形,∴PF=AE.∵AF∥PE,∴∠EPB=∠ACB.∵AB=AC,∴∠B=∠ACB,∴∠B=∠EPB,∴BE=PE,∴PE=PF+AB.21*cnjy*com
25.解:(1)由已知可得BP=2t cm,DQ=t cm,∴AQ=(12-t)cm.∵四边形ABPQ为平行四边形,∴12-t=2t,∴t=4,∴当t=4时,四边形ABPQ为平行四边形.
(2)过A作AE⊥BC于E,在Rt△ABE中,∠AEB=90°,
AB=2 cm,∠B=45°,∴AE=BE.
由勾股定理可知AB2=AE2+BE2,
∴AE= cm.
∴S四边形ABPQ=(BP+AQ)·AE=(12+t),
即y=(12+t).
(3)由(2)得S?ABCD=×12=12(cm2).∵×12=(12+t),∴t=6,∴BP=2×6=12(cm),
∴BP=BC,∴当点P与点C重合时,四边形ABPQ的面积是?ABCD面积的四分之三.
一、选择题(每题3分,共30分)
1.在?ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A.1∶2∶3∶4 B.1∶2∶1∶2
C.1∶1∶2∶2 D.1∶2∶2∶1
2.如图,在?ABCD中,已知AD=12 cm,AB=8 cm,AE平分∠BAD交BC边于点E,则CE的长等于( )【来源:21cnj*y.co*m】
A.8 cm B.6 cm C.4 cm D.2 cm
3.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长为( )
A.7 B.10 C.11 D.12
4.若平行四边形的一边长为10,则它的两条对角线长可以是( )
A.8和16 B.6和8 C.6和12 D.24和4
5.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A.变大 B.变小
C.不变 D.变大变小要看点P向左还是向右移动
6.在如图的网格中,以格点A、B、C、D、E、F中的4个点为顶点,共能画出平行四边形( )
A.2个 B.3个 C.4个 D.5个
7.四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能判定这个四边形是平行四边形的是( )21教育名师原创作品
A.AB=CD B.AD∥BC
C.OA=OC D.AC=BD
8.如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
9.如图,在平行四边形ABCD中,点E在AD上,连结CE并延长与BA的延长线交于点F,若AE=ED,CD=3 cm,则BF的长为( )
A.5 cm B.6 cm C.7 cm D.8 cm
10.如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、AD于E、F,再分别以E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=DH,③△ADH是等腰三角形,④S△ADH=S四边形ABCH.其中正确的有( )21世纪教育网版权所有
A.①②③ B.①③④ C.②④ D.①③
二、填空题(每题3分,共21分)
11.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2.则?ABCD的周长等于______________.21·cn·jy·com
12.如图,E是平行四边形内任一点,若S?ABCD=8,则图中阴影部分的面积是______________.
13.如图,在平行四边形ABCD中,AE⊥BC于E, AF⊥CD交DC的延长线于F ,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为_____________.
14.如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为_____________.?
15.在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=BC,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO,其中能够判定四边形ABCD是平行四边形的有_____________.?21教育网
16.如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称,若E点的坐标是(7,-3),则点A的坐标是_____________.
17.如图,在平行四边形AOBC中,对角线交于点E,双曲线y=(k>0)经过A,E两点,若平行四边形AOBC的面积为24,则k=_____________.
三、解答题( 18,19题每题5分,25题9分,其余每题6分,共49分)
18.已知:点P是?ABCD的对角线AC的中点,经过点P的直线EF交AB于点E,交DC于点F.
求证:AE=CF.
19.如图,在?ABCD中,E、F是对角线AC上的两点,且AE=CF,连结DE、BF.
(1)写出图中所有的全等三角形.
(2)求证:DE∥BF.
20.如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
21.如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE≌△DFE;
(2)连结BD、AF,试判断四边形ABDF的形状,并证明你的结论.
22.已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.
求证:四边形ABOE、四边形DCOE都是平行四边形.
23.如图,在四边形ABCD中,∠ADB=∠CBD=90°,BE∥CD交AD于E,且EA=EB.若AB=4,DB=4.www.21-cn-jy.com
求四边形ABCD的面积.
24.如图①,已知在△ABC中,AB=AC,点P为底边BC上(端点B、C除外)任意一点,且PE∥AC交AB于E,PF∥AB交AC于F.【来源:21·世纪·教育·网】
(1)试问线段PE、PF、AB之间有什么数量关系,并说明理由.
(2)如图②,将“点P为底边BC上任意一点”改为“点P为底边BC延长线上任意一点”,其他条件不变,上述结论还成立吗?如果不成立,你能得到什么结论?请说明你的理由.21·世纪*教育网
25.如图,在平行四边形ABCD中,AB=2 cm,BC=12 cm,∠B=45°,点P在边BC上,由点B向点C运动,速度为每秒2 cm,点Q在边AD上,与点P同时出发,由点D向点A运动,速度为每秒1 cm,连结PQ,设运动时间为t s.2·1·c·n·j·y
(1)当t为何值时,四边形ABPQ为平行四边形?
(2)设四边形ABPQ的面积为y cm2,请用含有t的代数式表示y;
(3)当点P运动至何处时,四边形ABPQ的面积是?ABCD面积的四分之三?
参考答案
一、1.【答案】B
解:由于平行四边形对角相等,所以对角的比数应该相等,其中A,C,D都不满足,只有B满足.故选B.
2.【答案】C
3.【答案】B
解:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
4.【答案】A
解:在?ABCD中,AD=10,对角线相交于O点,根据平行四边形的性质推出OA=OC=AC,OB=OD=BD,求出每个选项中OA和OD的长度,看看线段OA、OD、AD是否能围成三角形(即是否符合三角形的三边关系)即可.
5.【答案】C
解:设平行线AB、CD间的距离为h,则S△PCD=CD·h.∵CD的长度不变,h的大小不变,∴三角形PCD的面积不变.故选C.www-2-1-cnjy-com
6.【答案】B
解:观察题图可知,有?ABEC,?BDEC,?BEFC共3个.故选B.
7.【答案】D 8.【答案】C 9.【答案】B
10.【答案】D
二、11.【答案】20
解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC.∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE.∵AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴?ABCD的周长=4+4+6+6=20,故答案为20.21cnjy.com
12.【答案】4
13.【答案】48
解:设BC=x,则CD=20-x,根据“等面积法”得4x=6(20-x),解得x=12,∴BC=12,∴平行四边形ABCD的面积为AE·BC=4×12=48.
14.【答案】6
解:∵四边形DCFE是平行四边形,∴DE=CF,DE∥CF,∴△DEB的面积为四边形DCFE面积的一半.∵BC=4CF,∴DE=BC.设△ABC中BC边上的高为h,则S△ADE+S△DEB=DE·h=·BC·h=×24=6.21*cnjy*com
15.【答案】①②③④ 16.【答案】(-2,0)
17.【答案】8
解:设A(x,),B(a,0),过点A作AD⊥OB于点D,过点E作EF⊥OB于点F,如图,
由平行四边形的性质可知AE=EB,
∴E.
∵点E在双曲线上,∴·=k,∴a=3x.∵平行四边形的面积是24,∴a·=3x·=3k=24,∴k=8.【版权所有:21教育】
三、18.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠DCA=∠BAC.
又∵点P是AC的中点,∴AP=CP.
在△FCP和△EAP中,
∴△FCP≌△EAP,
∴AE=CF.
19.(1)解:△AED≌△CFB,△ABF≌△CDE,△ABC≌△CDA.
(2)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC.∴∠DAC=∠BCA,
在△ADE和△CBF中,
∴△ADE≌△CBF.∴∠AED=∠CFB.
∴∠DEC=∠AFB.∴DE∥BF.
20.解:(1)∵四边形ABCD是平行四边形,∴AD∥CB,∴∠DAB+∠CBA=180°.又∵AP和BP分别平分∠DAB和∠CBA,∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,∴在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°.
(2)∵AP平分∠DAB且AB∥CD,∴∠DAP=∠PAB=∠DPA,∴△ADP是等腰三角形,∴DP=AD=5 cm.同理可得PC=CB=5 cm,即AB=DC=DP+PC=10 cm.在Rt△APB中,∵∠APB=90°,AB=10 cm,AP=8 cm,∴BP==6(cm),∴△APB的周长为AB+AP+BP=10+8+6=24(cm). 2-1-c-n-j-y
21.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CF,∴∠BAD=∠ADF,∠ABE=∠DFE.∵E是AD的中点,∴AE=DE,∴△ABE≌△DFE.
(2)解:如图,四边形ABDF是平行四边形.
证明:∵△ABE≌△DFE,∴AB=DF.又∵AB∥DF,
∴四边形ABDF是平行四边形.
22.证明:∵在?ABCD中,对角线AC交BD于点O,∴OB=OD.又∵四边形AODE是平行四边形,∴AE∥OD且AE=OD,∴AE∥OB且AE=OB,∴四边形ABOE是平行四边形,∴AB∥OE,且AB=OE.又∵在?ABCD中,AB∥CD,AB=CD,∴OE∥CD,OE=CD,∴四边形DCOE也是平行四边形.
23.解:∵∠ADB=∠CBD=90°,∴DE∥CB.∵BE∥CD,∴四边形BEDC是平行四边形,∴BC=DE.在Rt△ABD中,由勾股定理得AD===8.设DE=x,则EA=8-x,∴EB=EA=8-x.在Rt△BDE中,由勾股定理得 DE2+DB2=EB2,∴x2+42=(8-x)2.解得x=3.∴BC=DE=3,∴S四边形ABCD=S△ABD+S△BDC=AD·DB+DB·BC=16+6=22.
24.解:(1)PE+PF=AB.理由:∵PE∥AC,PF∥AB,∴四边形AEPF是平行四边形,∴AE=PF.∵PE∥AC,∴∠EPB=∠C.又∵AB=AC,∴∠B=∠C=∠EPB,∴BE=PE,∴PE+PF=AB.【出处:21教育名师】
(2)不成立,结论为PE=PF+AB.理由:∵PE∥AC,PF∥AB,∴四边形AFPE是平行四边形,∴PF=AE.∵AF∥PE,∴∠EPB=∠ACB.∵AB=AC,∴∠B=∠ACB,∴∠B=∠EPB,∴BE=PE,∴PE=PF+AB.21*cnjy*com
25.解:(1)由已知可得BP=2t cm,DQ=t cm,∴AQ=(12-t)cm.∵四边形ABPQ为平行四边形,∴12-t=2t,∴t=4,∴当t=4时,四边形ABPQ为平行四边形.
(2)过A作AE⊥BC于E,在Rt△ABE中,∠AEB=90°,
AB=2 cm,∠B=45°,∴AE=BE.
由勾股定理可知AB2=AE2+BE2,
∴AE= cm.
∴S四边形ABPQ=(BP+AQ)·AE=(12+t),
即y=(12+t).
(3)由(2)得S?ABCD=×12=12(cm2).∵×12=(12+t),∴t=6,∴BP=2×6=12(cm),
∴BP=BC,∴当点P与点C重合时,四边形ABPQ的面积是?ABCD面积的四分之三.
