第20章 数据的整理与初步处理 单元测试卷
文档属性
| 名称 | 第20章 数据的整理与初步处理 单元测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 516.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-04 00:00:00 | ||
图片预览




文档简介
第20章 数据的整理与初步处理 单元测试卷
一、选择题(每题3分,共30分)
1.下表是山西省11个地市5月份某日最高气温(℃)的统计结果:
太原
大同
朔州
忻州
阳泉
晋中
吕梁
长治
晋城
临汾
运城
27
27
28
28
27
29
28
28
30
30
31
该日最高气温的众数和中位数分别是( )
A.27℃,28℃ B.28℃,28℃ C.27℃,27℃ D.28℃,29℃
2.李华根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表中数据一定不发生变化的是( )
A.平均数 B.众数 C.方差 D.中位数
3.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是=36,=30,则两组成绩的稳定性:( )2-1-c-n-j-y
A.甲组比乙组的成绩稳定
B.乙组比甲组的成绩稳定
C.甲、乙两组的成绩一样稳定
D.无法确定
4.为了解某公司员工的年工资情况,小王随机调查了10名员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司员工年工资中等水平的是( )
A.方差 B.众数 C.中位数 D.平均数
5.某班七个合作学习小组的人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )21*cnjy*com
A.5 B.5.5 C.6 D.7
6.有19名同学参加歌咏比赛,成绩互不相同,前10名的同学进入决赛,某同学知道自己的成绩后,要判断自己能否进入决赛,他只需知道这19名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
7.某班期末考试英语的平均成绩为75分,方差为225,如果每名学生都多考5分,下列说法正确的是( )21世纪教育网版权所有
A.平均分不变,方差不变 B.平均分变大,方差不变
C.平均分不变,方差变大 D.平均分变大,方差变大
8.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:
队员1
队员2
队员3
队员4
队员5
甲队
177
176
175
172
175
乙队
170
175
173
174
183
设甲、乙两队队员身高的平均数分别为,,身高的方差分别为,,则下列关系中完全正确的是( )
A.=,> B.=,<
C.>,> D.<,<
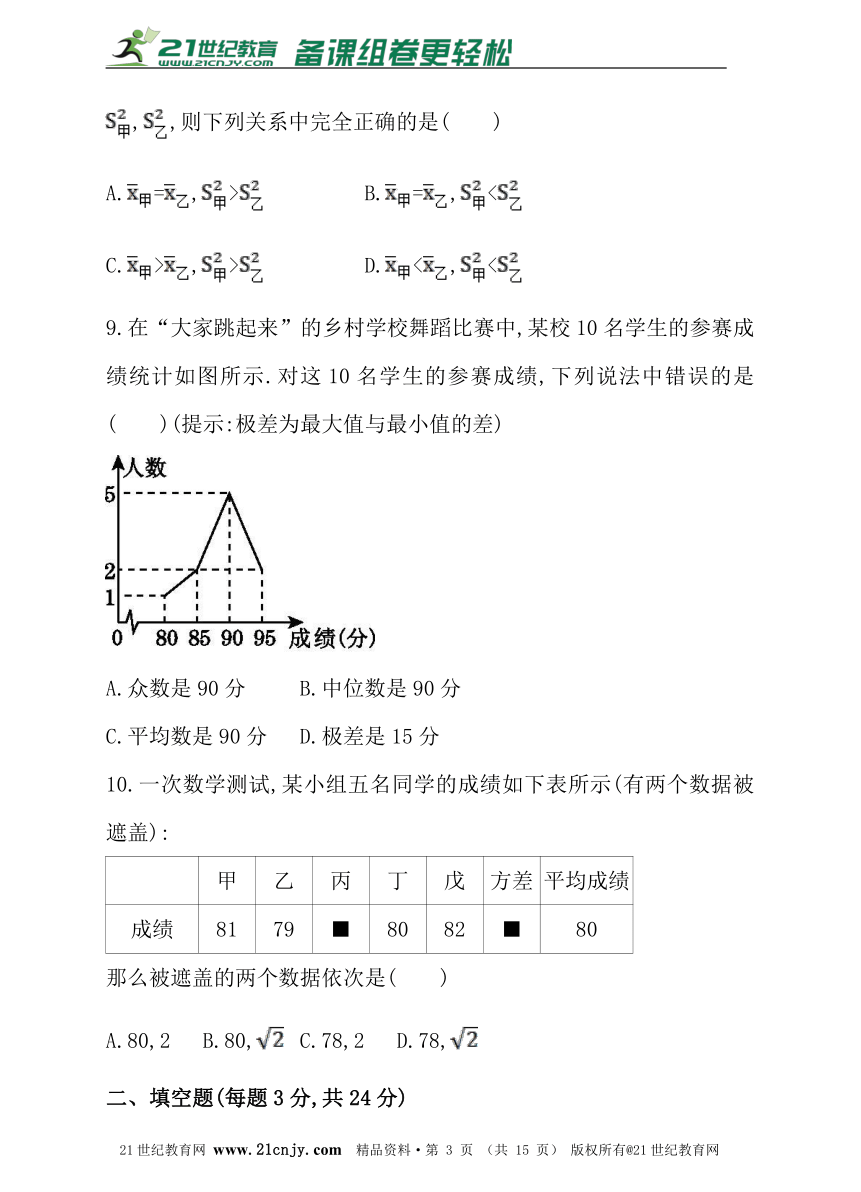
9.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生的参赛成绩统计如图所示.对这10名学生的参赛成绩,下列说法中错误的是( )(提示:极差为最大值与最小值的差)21*cnjy*com
A.众数是90分 B.中位数是90分
C.平均数是90分 D.极差是15分
10.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖):
甲
乙
丙
丁
戊
方差
平均成绩
成绩
81
79
■
80
82
■
80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
二、填空题(每题3分,共24分)
11.一组正整数2、3、4、x从小到大排列,已知这组数据的中位数和平均数相等,那么x的值是____________.?
12.某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是___________岁.?
13.为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数是___________小时.
14.x1,x2,…,x10的平均数为a,x11,x12,…,x50的平均数为b,则x1,x2,…,x50的平均数为___________.?
15.有一组数据:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是___________.?
16.已知2a1+3,2a2+3,2a3+3,2a4+3,…,2an+3的平均数是13,方差是36,则a1,a2,a3,a4,…,an的平均数和方差分别是___________、___________.?
17.跳远运动员李刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这6次成绩的平均数为7.8 m,方差为.如果李刚再跳两次,成绩分别为7.7 m,7.9 m.则李刚这8次跳远成绩的方差___________ (填“变大”、“不变”或“变小”).?
18.某次跳绳比赛中,甲、乙两班学生每分钟跳绳的成绩情况如下表:
班级
参加人数
平均数(次)
中位数(次)
方差
甲
45
135
149
180
乙
45
135
151
130
下列三个结论:
①甲班的平均成绩低于乙班的平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).
其中正确的结论是___________.(只填序号)?
三、解答题(23题10分,其余每题9分,共46分)
19.学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁; 21教育网
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两位选手的平均成绩,从他们的这一成绩看,应选派谁.21·cn·jy·com
20.八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每道题答对得5分,答错扣2分,未答得0分.赛后A、B、C、D、E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:【来源:21·世纪·教育·网】
参赛同学
答对题数(道)
答错题数(道)
未答题数(道)
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
(1)根据以上信息,求A、B、C、D四位同学成绩的平均分;
(2)最后获知:A、B、C、D、E五位同学的成绩分别是95分,81分,64分,83分,58分.
①求E同学答对的题数和答错的题数;
②经计算,A、B、C、D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出是哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).2·1·c·n·j·y
21.某厂生产A,B两种产品.其单价随市场变化而进行相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线统计图: www-2-1-cnjy-com
A,B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元)
6
5.2
6.5
B产品单价(元)
3.5
4
3
并求得A产品三次单价的平均数和方差如下:
=5.9(元);==.
(1)补全图中B产品单价变化的折线统计图.B产品第三次的单价比上一次的单价降低了_____________%;【出处:21教育名师】
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小:
(3)该厂决定第四次调价,A产品的单价仍为6.5元,B产品的单价比3元上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.21教育名师原创作品
22.在八次数学测试中,甲、乙两人的成绩(单位:分)如下:
甲:89,93,88,91,94,90,88,87; 乙:92,90,85,93,95,86,87,92.
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人成绩的极差,并说明谁的成绩变化范围大(极差:最大值与最小值的差);
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定.
23.为了了解学生关注热点新闻的情况,“两会”期间,小明对本班全体同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
根据上述信息,解答下列各题:
(1)该班女生人数是__________人,女生收看“两会”新闻次数的中位数是_________次;?
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班男生对“两会”新闻的“关注指数”比女生低5%,试求该班男生有多少人;
(3)为进一步分析该班男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如下表).
统计量
平均数(次)
中位数(次)
众数(次)
方差
该班男生
3
3
4
2
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班男、女生收看“两会”新闻次数的波动大小.
参考答案
一、1.【答案】B
解:28 ℃出现了4次,出现的次数最多,所以众数为28℃,将这组数由小到大排列
为:27 ℃,27 ℃,27 ℃,28 ℃,28 ℃,28 ℃,28 ℃,29 ℃,30 ℃,30 ℃,31 ℃,所以,中位数为28 ℃,选B.
2.【答案】D
3.【答案】B
解:方差小的比较稳定,故选B.
4.【答案】C
5.【答案】C
解:∵4、5、5、x、6、7、8的平均数是6,
∴(4+5+5+x+6+7+8)÷7=6,解得:x=7.
将这组数据从小到大排列为4、5、5、6、7、7、8,
最中间的数是6,则这组数据的中位数是6.故选C.
6.【答案】B
7.【答案】B
解:每名学生都多考5分,则平均分增加5分,但方差不变.故选B.
8.【答案】B
9.【答案】C
解:根据折线图可得下表:
人数
1
2
5
2
成绩(分)
80
85
90
95
由上表可知,成绩的众数是90分,中位数是90分,平均数是×(80+85×2+90×5+95×2)=89(分),极差是95-80=15(分).由此可见,本题中说法错误的是C.www.21-cn-jy.com
10.【答案】C
解:根据题意得:丙的成绩为80×5-(81+79+80+82)=78,方差为 [(81-80)2+(79-80)2+(78-80)2+(80-80)2+(82-80)2]÷5=2.
二、11.【答案】5
解:∵这组数据的中位数和平均数相等,
∴(3+4)÷2=(2+3+4+x)÷4,
解得:x=5.故答案为:5.
12.【答案】15
解:40名同学中,按照年龄大小排列,处于第20与21位上的年龄分别是15岁、15岁,这两数的平均数还是15岁,故这个班同学年龄的中位数是15岁.21cnjy.com
13.【答案】1
14.【答案】
解:本题中共有50个数据,x1,x2,…,x10的平均数为a,则它们的和为10a;x11,x12,…,x50的平均数为b,则它们的和为40b,所以x1,x2,…,x50的平均数为=.21·世纪*教育网
15.【答案】2
16.【答案】5;9
解:∵2a1+3,2a2+3,2a3+3,2a4+3,…,2an+3的平均数是13,方差是36,∴2a1,2a2,2a3,2a4,…,2an的平均数是10,方差是36,∴a1,a2,a3,a4,…,an的平均数是5,方差是9.
17.【答案】变小
解:∵李刚再跳两次后,这组数据的平均数是=7.8,∴这8次跳远成绩的方差是: [(7.6-7.8)2+(7.8-7.8)2+2×(7.7-7.8)2+(7.8-7.8)2+(8.0-7.8)2+2×(7.9-7.8)2]÷8=,∵<,∴方差变小.
18.【答案】②③
解:两个班的平均成绩均为135次,故①错误;方差表示数据的波动大小,甲班的方差大于乙班的方差,说明甲班成绩的波动比乙班成绩的波动大,故②正确;中位数是数据按大小排列后,中间的一个数或中间两数的平均数,甲班成绩的中位数小于150次,乙班成绩的中位数大于150次,且甲、乙两班参加人数相同,说明甲班成绩优秀人数少于乙班成绩优秀人数,故③正确.故答案为②③.
三、19.解:(1)乙的平均成绩为:
=79.5.
∵80.25>79.5,∴应选派甲.
(2)甲的平均成绩为:
=79.5.
乙的平均成绩为:
=80.4
∵79.5<80.4,∴应选派乙.
20.解:(1)=
82.5(分).
所以A、B、C、D四位同学成绩的平均分是82.5分.
(2)①设E同学答对x道题,答错y道题.
由题意,得解得
所以E同学答对12道题,答错1道题.
②C同学记错了;他实际答对14道题,答错3道题,未答3道题.
21.解:(1)如图所示.25
(2)=(3.5+4+3)=3.5(元),
==.
∵<,∴B产品的单价波动小.
(3)第四次调价后,
对于A产品,这四次单价的中位数为=(元);
对于B产品,∵m>0,∴第四次单价大于3元.
又∵×2-1=>,∴第四次单价小于4元.
∴×2-1=,∴m=25.
22.解:(1)甲成绩的极差为:94-87=7(分),乙成绩的极差为:95-85=10(分),
∴乙的成绩变化范围大.
(2)甲成绩的平均数为:(89+93+88+91+94+90+88+87)÷8=90(分),乙成绩的平均数为:(92+90+85+93+95+86+87+92)÷8=90(分),∴从平均数的角度看,两人的成绩一样好.【版权所有:21教育】
(3)甲成绩的众数为88分,乙成绩的众数为92分,∴从众数的角度看,乙的成绩较优.
(4)甲成绩的中位数为89.5分,乙成绩的中位数为91分,∴从中位数的角度看,乙的成绩较优.
(5)甲成绩的方差
为:[(89-90)2+(93-90)2+(88-90)2+(91-90)2+(94-90)2+(90-90)2+(88-90)2+(87-90)2]÷8=5.5,【来源:21cnj*y.co*m】
乙成绩的方差
为:[(92-90)2+(90-90)2+(85-90)2+(93-90)2+(95-90)2+(86-90)2+(87-90)2+(92-90)2]÷8=11.5,∴甲的成绩更稳定.
23.解:(1)20;3
(2)由题意得,该班女生对“两会”新闻的“关注指数”为×100%=65%,所以该班男生对“两会”新闻的“关注指数”为65%-5%=60%.设该班男生有x人,则60%x=x-(1+3+6),解得:x=25.所以该班男生有25人.
(3)该班女生收看“两会”新闻次数的平均数为
=3(次),
该班女生收看“两会”新闻次数的方差为:
=.
因为2>,所以该班男生比女生收看“两会”新闻次数的波动大.
一、选择题(每题3分,共30分)
1.下表是山西省11个地市5月份某日最高气温(℃)的统计结果:
太原
大同
朔州
忻州
阳泉
晋中
吕梁
长治
晋城
临汾
运城
27
27
28
28
27
29
28
28
30
30
31
该日最高气温的众数和中位数分别是( )
A.27℃,28℃ B.28℃,28℃ C.27℃,27℃ D.28℃,29℃
2.李华根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表中数据一定不发生变化的是( )
A.平均数 B.众数 C.方差 D.中位数
3.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是=36,=30,则两组成绩的稳定性:( )2-1-c-n-j-y
A.甲组比乙组的成绩稳定
B.乙组比甲组的成绩稳定
C.甲、乙两组的成绩一样稳定
D.无法确定
4.为了解某公司员工的年工资情况,小王随机调查了10名员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司员工年工资中等水平的是( )
A.方差 B.众数 C.中位数 D.平均数
5.某班七个合作学习小组的人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )21*cnjy*com
A.5 B.5.5 C.6 D.7
6.有19名同学参加歌咏比赛,成绩互不相同,前10名的同学进入决赛,某同学知道自己的成绩后,要判断自己能否进入决赛,他只需知道这19名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
7.某班期末考试英语的平均成绩为75分,方差为225,如果每名学生都多考5分,下列说法正确的是( )21世纪教育网版权所有
A.平均分不变,方差不变 B.平均分变大,方差不变
C.平均分不变,方差变大 D.平均分变大,方差变大
8.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:
队员1
队员2
队员3
队员4
队员5
甲队
177
176
175
172
175
乙队
170
175
173
174
183
设甲、乙两队队员身高的平均数分别为,,身高的方差分别为,,则下列关系中完全正确的是( )
A.=,> B.=,<
C.>,> D.<,<
9.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生的参赛成绩统计如图所示.对这10名学生的参赛成绩,下列说法中错误的是( )(提示:极差为最大值与最小值的差)21*cnjy*com
A.众数是90分 B.中位数是90分
C.平均数是90分 D.极差是15分
10.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖):
甲
乙
丙
丁
戊
方差
平均成绩
成绩
81
79
■
80
82
■
80
那么被遮盖的两个数据依次是( )
A.80,2 B.80, C.78,2 D.78,
二、填空题(每题3分,共24分)
11.一组正整数2、3、4、x从小到大排列,已知这组数据的中位数和平均数相等,那么x的值是____________.?
12.某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是___________岁.?
13.为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数是___________小时.
14.x1,x2,…,x10的平均数为a,x11,x12,…,x50的平均数为b,则x1,x2,…,x50的平均数为___________.?
15.有一组数据:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是___________.?
16.已知2a1+3,2a2+3,2a3+3,2a4+3,…,2an+3的平均数是13,方差是36,则a1,a2,a3,a4,…,an的平均数和方差分别是___________、___________.?
17.跳远运动员李刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这6次成绩的平均数为7.8 m,方差为.如果李刚再跳两次,成绩分别为7.7 m,7.9 m.则李刚这8次跳远成绩的方差___________ (填“变大”、“不变”或“变小”).?
18.某次跳绳比赛中,甲、乙两班学生每分钟跳绳的成绩情况如下表:
班级
参加人数
平均数(次)
中位数(次)
方差
甲
45
135
149
180
乙
45
135
151
130
下列三个结论:
①甲班的平均成绩低于乙班的平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数(跳绳次数≥150次为优秀).
其中正确的结论是___________.(只填序号)?
三、解答题(23题10分,其余每题9分,共46分)
19.学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁; 21教育网
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两位选手的平均成绩,从他们的这一成绩看,应选派谁.21·cn·jy·com
20.八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每道题答对得5分,答错扣2分,未答得0分.赛后A、B、C、D、E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:【来源:21·世纪·教育·网】
参赛同学
答对题数(道)
答错题数(道)
未答题数(道)
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
(1)根据以上信息,求A、B、C、D四位同学成绩的平均分;
(2)最后获知:A、B、C、D、E五位同学的成绩分别是95分,81分,64分,83分,58分.
①求E同学答对的题数和答错的题数;
②经计算,A、B、C、D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出是哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).2·1·c·n·j·y
21.某厂生产A,B两种产品.其单价随市场变化而进行相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线统计图: www-2-1-cnjy-com
A,B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元)
6
5.2
6.5
B产品单价(元)
3.5
4
3
并求得A产品三次单价的平均数和方差如下:
=5.9(元);==.
(1)补全图中B产品单价变化的折线统计图.B产品第三次的单价比上一次的单价降低了_____________%;【出处:21教育名师】
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小:
(3)该厂决定第四次调价,A产品的单价仍为6.5元,B产品的单价比3元上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.21教育名师原创作品
22.在八次数学测试中,甲、乙两人的成绩(单位:分)如下:
甲:89,93,88,91,94,90,88,87; 乙:92,90,85,93,95,86,87,92.
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人成绩的极差,并说明谁的成绩变化范围大(极差:最大值与最小值的差);
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定.
23.为了了解学生关注热点新闻的情况,“两会”期间,小明对本班全体同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
根据上述信息,解答下列各题:
(1)该班女生人数是__________人,女生收看“两会”新闻次数的中位数是_________次;?
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班男生对“两会”新闻的“关注指数”比女生低5%,试求该班男生有多少人;
(3)为进一步分析该班男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如下表).
统计量
平均数(次)
中位数(次)
众数(次)
方差
该班男生
3
3
4
2
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班男、女生收看“两会”新闻次数的波动大小.
参考答案
一、1.【答案】B
解:28 ℃出现了4次,出现的次数最多,所以众数为28℃,将这组数由小到大排列
为:27 ℃,27 ℃,27 ℃,28 ℃,28 ℃,28 ℃,28 ℃,29 ℃,30 ℃,30 ℃,31 ℃,所以,中位数为28 ℃,选B.
2.【答案】D
3.【答案】B
解:方差小的比较稳定,故选B.
4.【答案】C
5.【答案】C
解:∵4、5、5、x、6、7、8的平均数是6,
∴(4+5+5+x+6+7+8)÷7=6,解得:x=7.
将这组数据从小到大排列为4、5、5、6、7、7、8,
最中间的数是6,则这组数据的中位数是6.故选C.
6.【答案】B
7.【答案】B
解:每名学生都多考5分,则平均分增加5分,但方差不变.故选B.
8.【答案】B
9.【答案】C
解:根据折线图可得下表:
人数
1
2
5
2
成绩(分)
80
85
90
95
由上表可知,成绩的众数是90分,中位数是90分,平均数是×(80+85×2+90×5+95×2)=89(分),极差是95-80=15(分).由此可见,本题中说法错误的是C.www.21-cn-jy.com
10.【答案】C
解:根据题意得:丙的成绩为80×5-(81+79+80+82)=78,方差为 [(81-80)2+(79-80)2+(78-80)2+(80-80)2+(82-80)2]÷5=2.
二、11.【答案】5
解:∵这组数据的中位数和平均数相等,
∴(3+4)÷2=(2+3+4+x)÷4,
解得:x=5.故答案为:5.
12.【答案】15
解:40名同学中,按照年龄大小排列,处于第20与21位上的年龄分别是15岁、15岁,这两数的平均数还是15岁,故这个班同学年龄的中位数是15岁.21cnjy.com
13.【答案】1
14.【答案】
解:本题中共有50个数据,x1,x2,…,x10的平均数为a,则它们的和为10a;x11,x12,…,x50的平均数为b,则它们的和为40b,所以x1,x2,…,x50的平均数为=.21·世纪*教育网
15.【答案】2
16.【答案】5;9
解:∵2a1+3,2a2+3,2a3+3,2a4+3,…,2an+3的平均数是13,方差是36,∴2a1,2a2,2a3,2a4,…,2an的平均数是10,方差是36,∴a1,a2,a3,a4,…,an的平均数是5,方差是9.
17.【答案】变小
解:∵李刚再跳两次后,这组数据的平均数是=7.8,∴这8次跳远成绩的方差是: [(7.6-7.8)2+(7.8-7.8)2+2×(7.7-7.8)2+(7.8-7.8)2+(8.0-7.8)2+2×(7.9-7.8)2]÷8=,∵<,∴方差变小.
18.【答案】②③
解:两个班的平均成绩均为135次,故①错误;方差表示数据的波动大小,甲班的方差大于乙班的方差,说明甲班成绩的波动比乙班成绩的波动大,故②正确;中位数是数据按大小排列后,中间的一个数或中间两数的平均数,甲班成绩的中位数小于150次,乙班成绩的中位数大于150次,且甲、乙两班参加人数相同,说明甲班成绩优秀人数少于乙班成绩优秀人数,故③正确.故答案为②③.
三、19.解:(1)乙的平均成绩为:
=79.5.
∵80.25>79.5,∴应选派甲.
(2)甲的平均成绩为:
=79.5.
乙的平均成绩为:
=80.4
∵79.5<80.4,∴应选派乙.
20.解:(1)=
82.5(分).
所以A、B、C、D四位同学成绩的平均分是82.5分.
(2)①设E同学答对x道题,答错y道题.
由题意,得解得
所以E同学答对12道题,答错1道题.
②C同学记错了;他实际答对14道题,答错3道题,未答3道题.
21.解:(1)如图所示.25
(2)=(3.5+4+3)=3.5(元),
==.
∵<,∴B产品的单价波动小.
(3)第四次调价后,
对于A产品,这四次单价的中位数为=(元);
对于B产品,∵m>0,∴第四次单价大于3元.
又∵×2-1=>,∴第四次单价小于4元.
∴×2-1=,∴m=25.
22.解:(1)甲成绩的极差为:94-87=7(分),乙成绩的极差为:95-85=10(分),
∴乙的成绩变化范围大.
(2)甲成绩的平均数为:(89+93+88+91+94+90+88+87)÷8=90(分),乙成绩的平均数为:(92+90+85+93+95+86+87+92)÷8=90(分),∴从平均数的角度看,两人的成绩一样好.【版权所有:21教育】
(3)甲成绩的众数为88分,乙成绩的众数为92分,∴从众数的角度看,乙的成绩较优.
(4)甲成绩的中位数为89.5分,乙成绩的中位数为91分,∴从中位数的角度看,乙的成绩较优.
(5)甲成绩的方差
为:[(89-90)2+(93-90)2+(88-90)2+(91-90)2+(94-90)2+(90-90)2+(88-90)2+(87-90)2]÷8=5.5,【来源:21cnj*y.co*m】
乙成绩的方差
为:[(92-90)2+(90-90)2+(85-90)2+(93-90)2+(95-90)2+(86-90)2+(87-90)2+(92-90)2]÷8=11.5,∴甲的成绩更稳定.
23.解:(1)20;3
(2)由题意得,该班女生对“两会”新闻的“关注指数”为×100%=65%,所以该班男生对“两会”新闻的“关注指数”为65%-5%=60%.设该班男生有x人,则60%x=x-(1+3+6),解得:x=25.所以该班男生有25人.
(3)该班女生收看“两会”新闻次数的平均数为
=3(次),
该班女生收看“两会”新闻次数的方差为:
=.
因为2>,所以该班男生比女生收看“两会”新闻次数的波动大.
