七年级数学人教版下 5.2.2 平行线的判定 课件 (共25张PPT)
文档属性
| 名称 | 七年级数学人教版下 5.2.2 平行线的判定 课件 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-04 23:18:41 | ||
图片预览


文档简介
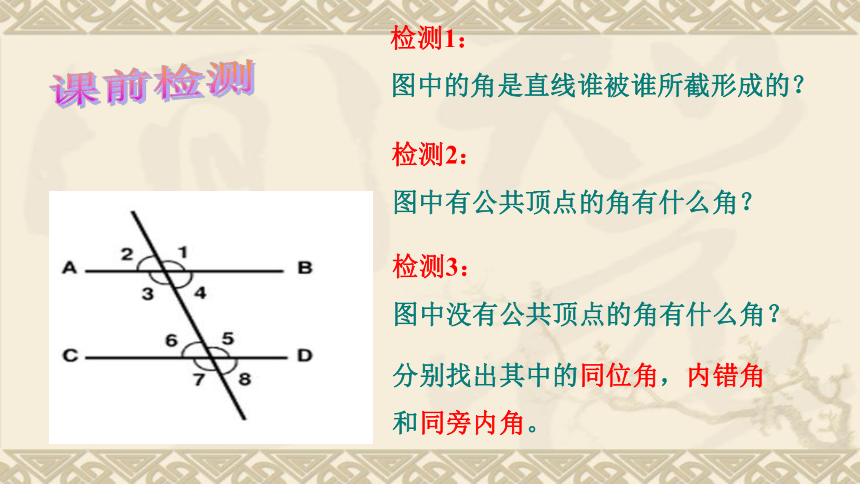
课件25张PPT。5.2.2 平行线的判定第五章 相交线与平行线课前检测检测1:
图中的角是直线谁被谁所截形成的?检测2:
图中有公共顶点的角有什么角?检测3:
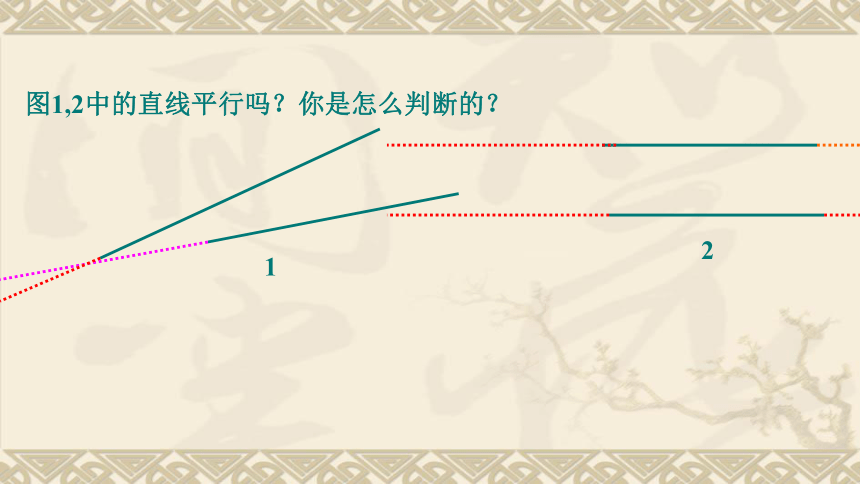
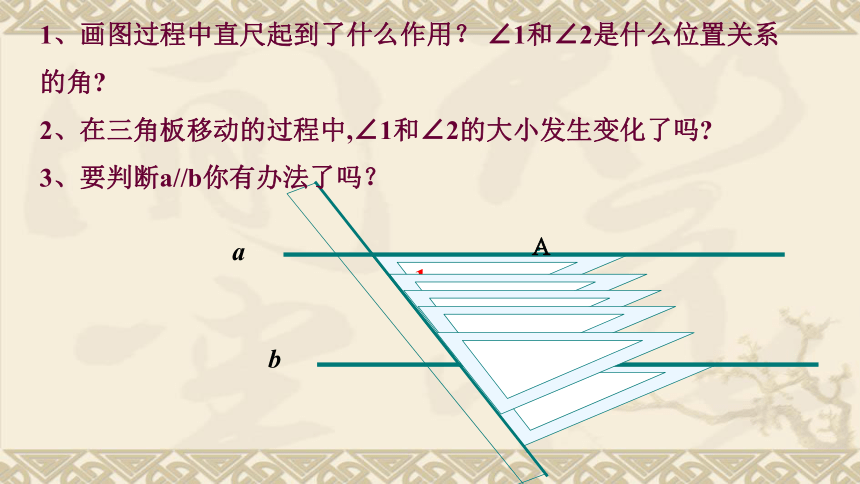
图中没有公共顶点的角有什么角?分别找出其中的同位角,内错角和同旁内角。 回顾 & 思考在同一平面内相交平行(完成下列填空) 两直线的位置关系: 的两直线叫做平行线.同一平面内,不相交还记得如何用三角板和直尺画平行线吗?一放、二靠、三推、四画。12图1,2中的直线平行吗?你是怎么判断的? 12ab.A1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
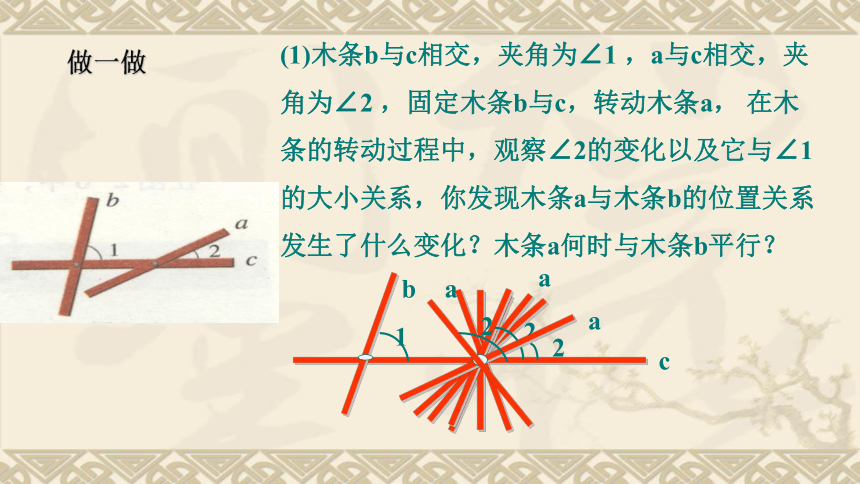
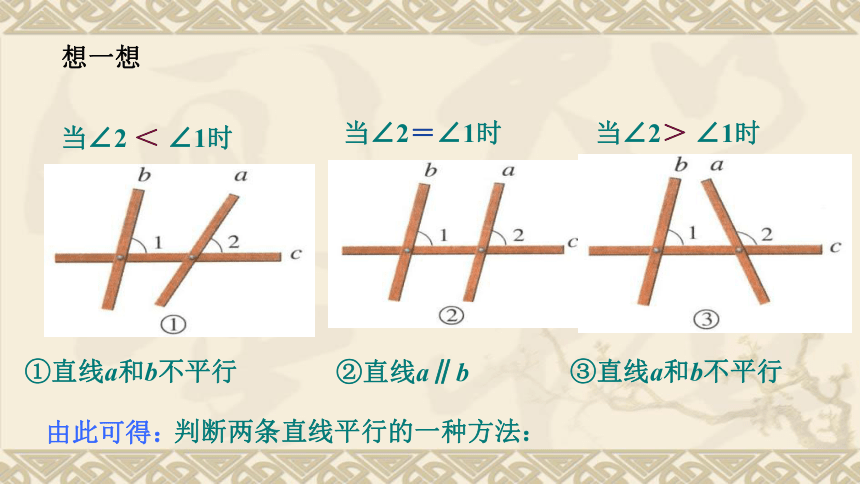
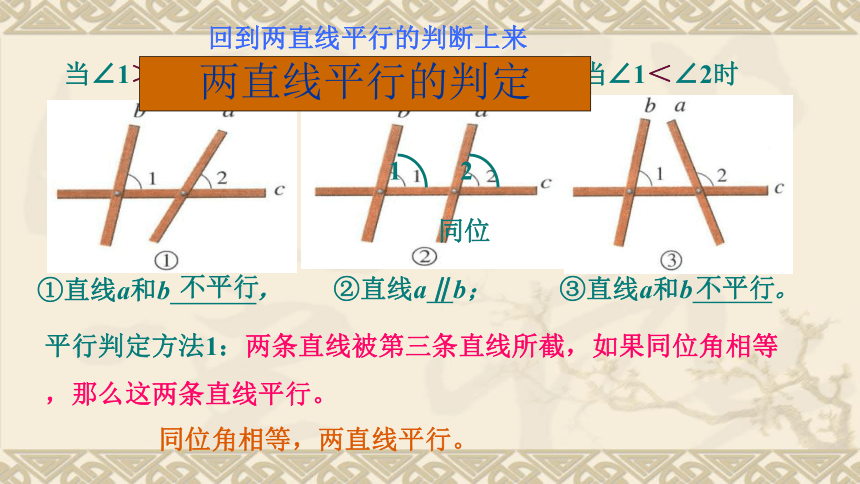
3、要判断a//b你有办法了吗?如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角多少度时,才能使木条a与木条b平行?怎样使得两根木条保持平行呢?答:当木条a与墙壁边缘成90度角时。(1)木条b与c相交,夹角为∠1 ,a与c相交,夹角为∠2 ,固定木条b与c,转动木条a, 在木条的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?做一做①直线a和b不平行②直线a∥b③直线a和b不平行想一想判断两条直线平行的一种方法:由此可得:平行判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。回到两直线平行的判断上来不平行∥不平行同位角相等,两直线平行。两直线平行的判定同位两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.∵∠1 = ∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行).符号语言①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。用判定定理1应该注意: 2.如果 , 能判定哪两条直线平行? ∠1 =∠2ABCEFDHG ∠3 =∠4∠2 =∠5想一想例题解析例1:如图,∠ 1= ∠C ,∠ 2= ∠C ,请找出图中互相平行的直线,并说明理由.解:AB∥CD,AC∥BD,理由如下:
∵∠1 = ∠C (已知)
∴ AB ∥ CD (同位角相等,两直线平行).
同理可得:AC∥BDBE∥CD(1)当∠2=∠3时, ∥b ;(2)当∠1=∠ 时,a∥b;(3)当∠3=∠4时,a∥b?练习 2a4证明:∵∠3=∠4 (已知)
∵∠3=∠1 (对顶角相等)
∴∠1=∠4 (等量代换)
∴a∥b (同位角相等,两直线平行) 如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。DE∵ ∠1 = ∠2 = 55° ∠3 = ∠2, ∴ ∠3 =∠1= 55° ∴ AB∥CD. 小小演练场( )对顶角相等 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?思考:F已知:直线AB、CD被EF所截,∠1=∠2,
求证:AB∥CD证明:
∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
∴AB∥CD (同位角相等,两直线平行) 由此你又获得怎样的判定平行线的方法?C判定方法2两条直线被第三条直线所截,如果内错角相等,那么两条直线平行。
几何语言表述: ∵∠1=∠2(已知)
∴AB∥CD(内错角相等,两直线平行)C已知∠3=45 °,∠1与∠2互余,试求出 解:∵∠1=∠2°(对顶角相等)
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁是高手AB//CD已知如图,∠1=75°,∠5=105°,
问: AB与CD平行吗?为什么?答:平行证明:∴ ∠1+∠5=180°∵ ∠1=75°,∠5=105° (已知)∵ ∠1+∠3=180° (邻补角定义)∴ ∠3=∠5 (同角的补角相等)∴ AB∥CD (内错角相等,两直线平行) 如果?1+?2=1800 能判定a//b吗?写出推理过程?c解:∵?1+?2=180°
?1+?3=180°
∴ ?2=?3
∴ a//b (同位角相等,两直线平行)说一说同旁内角互补,两直线平行。判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?解:这两条直线平行。∵ b⊥a c ⊥a
∴∠1=∠2 = 90 °
∴b ∥ c(同位角相等,两直线平行)
结论:在同一平面内,垂直于同一条直线的两条直线互相( ) 平行 同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
图中的角是直线谁被谁所截形成的?检测2:
图中有公共顶点的角有什么角?检测3:
图中没有公共顶点的角有什么角?分别找出其中的同位角,内错角和同旁内角。 回顾 & 思考在同一平面内相交平行(完成下列填空) 两直线的位置关系: 的两直线叫做平行线.同一平面内,不相交还记得如何用三角板和直尺画平行线吗?一放、二靠、三推、四画。12图1,2中的直线平行吗?你是怎么判断的? 12ab.A1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
3、要判断a//b你有办法了吗?如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角多少度时,才能使木条a与木条b平行?怎样使得两根木条保持平行呢?答:当木条a与墙壁边缘成90度角时。(1)木条b与c相交,夹角为∠1 ,a与c相交,夹角为∠2 ,固定木条b与c,转动木条a, 在木条的转动过程中,观察∠2的变化以及它与∠1的大小关系,你发现木条a与木条b的位置关系发生了什么变化?木条a何时与木条b平行?做一做①直线a和b不平行②直线a∥b③直线a和b不平行想一想判断两条直线平行的一种方法:由此可得:平行判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。回到两直线平行的判断上来不平行∥不平行同位角相等,两直线平行。两直线平行的判定同位两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.∵∠1 = ∠2 (已知)
∴ a ∥ b (同位角相等,两直线平行).符号语言①找出同位角;
②说明这两个同位角相等;
③得出“平行”的结论。用判定定理1应该注意: 2.如果 , 能判定哪两条直线平行? ∠1 =∠2ABCEFDHG ∠3 =∠4∠2 =∠5想一想例题解析例1:如图,∠ 1= ∠C ,∠ 2= ∠C ,请找出图中互相平行的直线,并说明理由.解:AB∥CD,AC∥BD,理由如下:
∵∠1 = ∠C (已知)
∴ AB ∥ CD (同位角相等,两直线平行).
同理可得:AC∥BDBE∥CD(1)当∠2=∠3时, ∥b ;(2)当∠1=∠ 时,a∥b;(3)当∠3=∠4时,a∥b?练习 2a4证明:∵∠3=∠4 (已知)
∵∠3=∠1 (对顶角相等)
∴∠1=∠4 (等量代换)
∴a∥b (同位角相等,两直线平行) 如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。DE∵ ∠1 = ∠2 = 55° ∠3 = ∠2, ∴ ∠3 =∠1= 55° ∴ AB∥CD. 小小演练场( )对顶角相等 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?思考:F已知:直线AB、CD被EF所截,∠1=∠2,
求证:AB∥CD证明:
∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
∴AB∥CD (同位角相等,两直线平行) 由此你又获得怎样的判定平行线的方法?C判定方法2两条直线被第三条直线所截,如果内错角相等,那么两条直线平行。
几何语言表述: ∵∠1=∠2(已知)
∴AB∥CD(内错角相等,两直线平行)C已知∠3=45 °,∠1与∠2互余,试求出 解:∵∠1=∠2°(对顶角相等)
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)看谁是高手AB//CD已知如图,∠1=75°,∠5=105°,
问: AB与CD平行吗?为什么?答:平行证明:∴ ∠1+∠5=180°∵ ∠1=75°,∠5=105° (已知)∵ ∠1+∠3=180° (邻补角定义)∴ ∠3=∠5 (同角的补角相等)∴ AB∥CD (内错角相等,两直线平行) 如果?1+?2=1800 能判定a//b吗?写出推理过程?c解:∵?1+?2=180°
?1+?3=180°
∴ ?2=?3
∴ a//b (同位角相等,两直线平行)说一说同旁内角互补,两直线平行。判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC想一想 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?解:这两条直线平行。∵ b⊥a c ⊥a
∴∠1=∠2 = 90 °
∴b ∥ c(同位角相等,两直线平行)
结论:在同一平面内,垂直于同一条直线的两条直线互相( ) 平行 同位角相等内错角相等同旁内角互补两直线平行平行线的判定示意图判定数量关系位置关系小结
