湖南省邵阳县黄亭市镇中学八年级数学(下)第一次月考试卷(含答案)
文档属性
| 名称 | 湖南省邵阳县黄亭市镇中学八年级数学(下)第一次月考试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-06 21:37:45 | ||
图片预览

文档简介
湘教版八年级数学(下)第一次月考试卷(含答案)
一、选择题(30分)
1、以下列各组数据中的三个数作三角形的三边,其中能构成直角三角形的是(
)
A.
,,;B.
1,,;
C.
6,7,8;D.
2,3,4;
2、如图,AC⊥BE于C,DF⊥BC于F,且BC=EF,如果添加一个条件后,可以直接用“HL”来证明Rt△ABC≌Rt△DEF,这个条件应该是(
)
A.
AC=DE;
B.
AB=DE;
C.
∠B=∠E;
D.
∠D=∠A;
3、已知一直角三角形的木板,三边长的平方和为800cm2,则斜边长为(
)
A.
40cm;
B.
20cm;
C.
80cm;
D.
30cm;
4、能使两个直角三角形全等的条件是(
)
A.
两条直角边对应相等;
B.
一个锐角对应相等;
C.
两个锐角对应相等;
D.
斜边对应相等;
5、如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD
的长是(
)
A.
20;
B.
10;
C.
5;
D.
;
6、如图,直角三角形三边上的半圆面积从小到大依次为S1、S2、S3,则S1、S2、S3的关系是(
)
A.
S1+S2=S3;
B.
S12+S22=S32;
C.
S1+S2>S3;
D.
S1+S27、等腰三角形腰长为10cm,底边长为16cm,则面积为(
)
A.
96cm2;
B.
48cm2;
C.
24cm2;
D.
32cm2;
8、如图,AB=BC=CD=DE=1,AB⊥BC,
AC⊥CD,AD⊥DE,则AE的长为(
)
A.
1;
B.
;
C.
;
D.
2;
9、如图,在Rt△ABC中,∠ACB=90°,CD、
CE分别是斜边AB上的高与中线,CF是
∠ACB的平分线,则∠1与∠2的关系是(
)
A.
∠1<∠2;
B.
∠1=∠2;
C.
∠1>∠2;
D.
不能确定;
10、已知a、b、c是三角形的三边长,如果
,那么△ABC是(
)
A.
以a为斜边的直角三角形;
B.
以b为斜边的直角三角形;
C.
以c为斜边的直角三角形;
D.
锐角三角形;
二、填空题(32分)
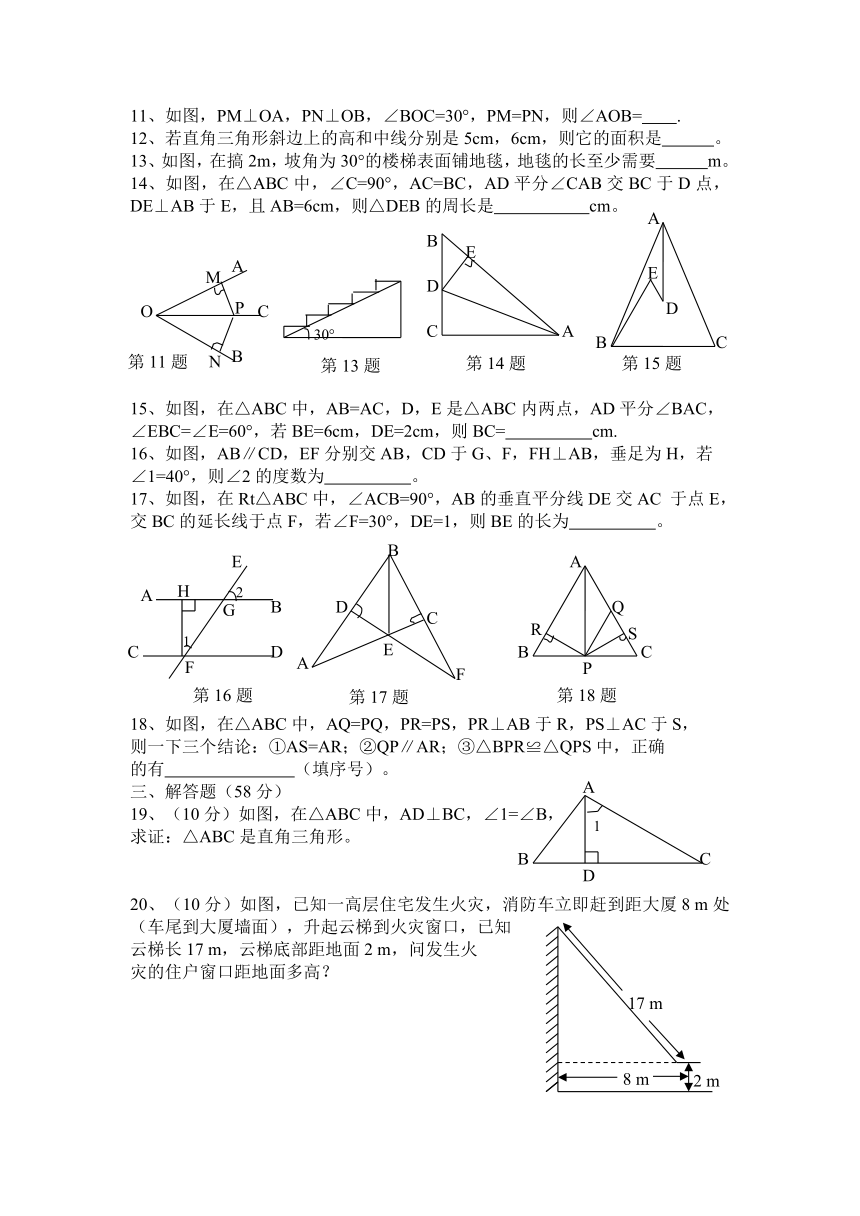
11、如图,PM⊥OA,PN⊥OB,∠BOC=30°,PM=PN,则∠AOB=
.
12、若直角三角形斜边上的高和中线分别是5cm,6cm,则它的面积是
。
13、如图,在搞2m,坡角为30°的楼梯表面铺地毯,地毯的长至少需要
m。
14、如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D点,DE⊥AB于E,且AB=6cm,则△DEB的周长是
cm。
15、如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,
∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=
cm.
16、如图,AB∥CD,EF分别交AB,CD于G、F,FH⊥AB,垂足为H,若
∠1=40°,则∠2的度数为
。
17、如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC
于点E,交BC的延长线于点F,若∠F=30°,DE=1,则BE的长为
。
18、如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,
则一下三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中,正确
的有
(填序号)。
三、解答题(58分)
19、(10分)如图,在△ABC中,AD⊥BC,∠1=∠B,
求证:△ABC是直角三角形。
20、(10分)如图,已知一高层住宅发生火灾,消防车立即赶到距大厦8
m处(车尾到大厦墙面),升起云梯到火灾窗口,已知
云梯长17
m,云梯底部距地面2
m,问发生火
灾的住户窗口距地面多高?
21、(12分)如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD,AF⊥CE,垂足分别是G,F,且AG=AF,求证:AD=AE;
22、(12分)台风过后,海上突然发来求教信号,海防队立即派出两条搜救船进行营救,由于无法知道出事海域的确切位置,于是派甲船向东北方向搜寻,派乙船向东南方向搜寻,甲船每小时行驶80海里,乙船每小时行驶150海里,半小时后,甲船收到乙船的信号,停止前进,乙船已到达出事地点,要求甲船立刻向乙船所在位置行进,请你计算,收到信号后甲船到达出事地点需要多长时间?
23、(14分)已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,
∠MBN=60°,∠MBN的两边分别交AD、DC(或它们的延长线)于E、F两点,
(1)当AE=CF时(如图①),求证:AE+CF=EF;
(2)当AE≠CF时,在如图②和如图③的两种情况下,AE+CF=EF是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需要证明?
参考答案:
一、1、B;2、B;3、C;4、A;5、C;6、A;7、B;8、D;9、B;10、C;
二、11、60°;12、30;13、;14、6;15、8;
16、50°;17、2;18、①②;
三、19、∵AD⊥BC,∴∠1+∠C=90°,又∠1=∠B,∴∠B+∠C=90°,
即∠B与∠C互余,∴△ABC是直角三角形。
20、设火灾窗口距地面(x+2)
m,由勾股定理得:x=15,
∴火灾窗口距地面17
m.
21、提示:先可证得:Rt△ABG≌Rt△ACF,得:∠BAG=∠CAF,
在证得:Rt△AFE≌Rt△AGD,∴AD=AE;
22、根据题意,画出图形,(如右图)
∠CAD=∠BAD=45°,即:∠CAB=90°,
AC=(海里),AB=(海里)
由勾股定理得:BC=85(海里)
∴收到信号后甲船到达出事地点需要:(小时)
23、(1)∵BC⊥CD,AB⊥AD,∴∠C=∠A=90°,
又AB=BC,AE=CF,∴Rt△BCF≌Rt△BAE(SAS),∴∠CBF=∠ABE,BF=BE
∵∠ABC=120°,∠MBN=60°,∴∠CBF=∠ABE=30°,∴△BFE是等边三角形。
BF=EF=BE,而CF=BF,AE=BE,∴CF+AE=BF+BE=EF.
(2)在图②的情况下,AE+CF=EF成立,证明如下:
如图,延长DC至G,使CG=AE,连接BG,
可证得:Rt△BCG≌Rt△BAE(SAS),GC=AE,
继而证得:△GBF≌Rt△EBF,
∴GF=EF,又GC+CF=GF,
∴AE+CF=GF=EF
在图③的情况下,AE+CF=EF不成立,
存在的关系是:AE-CF=EF.
A
B
C
D
E
F
第2题
A
B
C
D
第5题
S2
S1
S3
第6题
A
B
C
D
E
第8题
A
B
C
D
E
F
1
2
第9题
A
B
O
C
P
M
N
第11题
30°
第13题
A
B
C
D
E
第14题
A
B
C
D
E
第15题
A
B
C
D
E
F
H
G
1
2
第16题
A
B
C
D
E
F
第17题
A
B
C
P
Q
R
S
第18题
1
A
B
C
D
17
m
8
m
2
m
A
B
C
D
E
F
G
图①
A
B
C
D
E
F
M
N
图②
A
B
C
D
E
F
M
N
图③
A
B
C
D
E
F
M
N
D
南
北
A
B
C
图②
A
B
C
D
E
F
M
N
G
1
2
3
一、选择题(30分)
1、以下列各组数据中的三个数作三角形的三边,其中能构成直角三角形的是(
)
A.
,,;B.
1,,;
C.
6,7,8;D.
2,3,4;
2、如图,AC⊥BE于C,DF⊥BC于F,且BC=EF,如果添加一个条件后,可以直接用“HL”来证明Rt△ABC≌Rt△DEF,这个条件应该是(
)
A.
AC=DE;
B.
AB=DE;
C.
∠B=∠E;
D.
∠D=∠A;
3、已知一直角三角形的木板,三边长的平方和为800cm2,则斜边长为(
)
A.
40cm;
B.
20cm;
C.
80cm;
D.
30cm;
4、能使两个直角三角形全等的条件是(
)
A.
两条直角边对应相等;
B.
一个锐角对应相等;
C.
两个锐角对应相等;
D.
斜边对应相等;
5、如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD
的长是(
)
A.
20;
B.
10;
C.
5;
D.
;
6、如图,直角三角形三边上的半圆面积从小到大依次为S1、S2、S3,则S1、S2、S3的关系是(
)
A.
S1+S2=S3;
B.
S12+S22=S32;
C.
S1+S2>S3;
D.
S1+S2
)
A.
96cm2;
B.
48cm2;
C.
24cm2;
D.
32cm2;
8、如图,AB=BC=CD=DE=1,AB⊥BC,
AC⊥CD,AD⊥DE,则AE的长为(
)
A.
1;
B.
;
C.
;
D.
2;
9、如图,在Rt△ABC中,∠ACB=90°,CD、
CE分别是斜边AB上的高与中线,CF是
∠ACB的平分线,则∠1与∠2的关系是(
)
A.
∠1<∠2;
B.
∠1=∠2;
C.
∠1>∠2;
D.
不能确定;
10、已知a、b、c是三角形的三边长,如果
,那么△ABC是(
)
A.
以a为斜边的直角三角形;
B.
以b为斜边的直角三角形;
C.
以c为斜边的直角三角形;
D.
锐角三角形;
二、填空题(32分)
11、如图,PM⊥OA,PN⊥OB,∠BOC=30°,PM=PN,则∠AOB=
.
12、若直角三角形斜边上的高和中线分别是5cm,6cm,则它的面积是
。
13、如图,在搞2m,坡角为30°的楼梯表面铺地毯,地毯的长至少需要
m。
14、如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D点,DE⊥AB于E,且AB=6cm,则△DEB的周长是
cm。
15、如图,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,
∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=
cm.
16、如图,AB∥CD,EF分别交AB,CD于G、F,FH⊥AB,垂足为H,若
∠1=40°,则∠2的度数为
。
17、如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC
于点E,交BC的延长线于点F,若∠F=30°,DE=1,则BE的长为
。
18、如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,
则一下三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中,正确
的有
(填序号)。
三、解答题(58分)
19、(10分)如图,在△ABC中,AD⊥BC,∠1=∠B,
求证:△ABC是直角三角形。
20、(10分)如图,已知一高层住宅发生火灾,消防车立即赶到距大厦8
m处(车尾到大厦墙面),升起云梯到火灾窗口,已知
云梯长17
m,云梯底部距地面2
m,问发生火
灾的住户窗口距地面多高?
21、(12分)如图,AB=AC,点D、E分别在AC、AB上,AG⊥BD,AF⊥CE,垂足分别是G,F,且AG=AF,求证:AD=AE;
22、(12分)台风过后,海上突然发来求教信号,海防队立即派出两条搜救船进行营救,由于无法知道出事海域的确切位置,于是派甲船向东北方向搜寻,派乙船向东南方向搜寻,甲船每小时行驶80海里,乙船每小时行驶150海里,半小时后,甲船收到乙船的信号,停止前进,乙船已到达出事地点,要求甲船立刻向乙船所在位置行进,请你计算,收到信号后甲船到达出事地点需要多长时间?
23、(14分)已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,
∠MBN=60°,∠MBN的两边分别交AD、DC(或它们的延长线)于E、F两点,
(1)当AE=CF时(如图①),求证:AE+CF=EF;
(2)当AE≠CF时,在如图②和如图③的两种情况下,AE+CF=EF是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需要证明?
参考答案:
一、1、B;2、B;3、C;4、A;5、C;6、A;7、B;8、D;9、B;10、C;
二、11、60°;12、30;13、;14、6;15、8;
16、50°;17、2;18、①②;
三、19、∵AD⊥BC,∴∠1+∠C=90°,又∠1=∠B,∴∠B+∠C=90°,
即∠B与∠C互余,∴△ABC是直角三角形。
20、设火灾窗口距地面(x+2)
m,由勾股定理得:x=15,
∴火灾窗口距地面17
m.
21、提示:先可证得:Rt△ABG≌Rt△ACF,得:∠BAG=∠CAF,
在证得:Rt△AFE≌Rt△AGD,∴AD=AE;
22、根据题意,画出图形,(如右图)
∠CAD=∠BAD=45°,即:∠CAB=90°,
AC=(海里),AB=(海里)
由勾股定理得:BC=85(海里)
∴收到信号后甲船到达出事地点需要:(小时)
23、(1)∵BC⊥CD,AB⊥AD,∴∠C=∠A=90°,
又AB=BC,AE=CF,∴Rt△BCF≌Rt△BAE(SAS),∴∠CBF=∠ABE,BF=BE
∵∠ABC=120°,∠MBN=60°,∴∠CBF=∠ABE=30°,∴△BFE是等边三角形。
BF=EF=BE,而CF=BF,AE=BE,∴CF+AE=BF+BE=EF.
(2)在图②的情况下,AE+CF=EF成立,证明如下:
如图,延长DC至G,使CG=AE,连接BG,
可证得:Rt△BCG≌Rt△BAE(SAS),GC=AE,
继而证得:△GBF≌Rt△EBF,
∴GF=EF,又GC+CF=GF,
∴AE+CF=GF=EF
在图③的情况下,AE+CF=EF不成立,
存在的关系是:AE-CF=EF.
A
B
C
D
E
F
第2题
A
B
C
D
第5题
S2
S1
S3
第6题
A
B
C
D
E
第8题
A
B
C
D
E
F
1
2
第9题
A
B
O
C
P
M
N
第11题
30°
第13题
A
B
C
D
E
第14题
A
B
C
D
E
第15题
A
B
C
D
E
F
H
G
1
2
第16题
A
B
C
D
E
F
第17题
A
B
C
P
Q
R
S
第18题
1
A
B
C
D
17
m
8
m
2
m
A
B
C
D
E
F
G
图①
A
B
C
D
E
F
M
N
图②
A
B
C
D
E
F
M
N
图③
A
B
C
D
E
F
M
N
D
南
北
A
B
C
图②
A
B
C
D
E
F
M
N
G
1
2
3
同课章节目录
