湘教版八年级数学(下)第一章直角三角形 基础卷(含答案)
文档属性
| 名称 | 湘教版八年级数学(下)第一章直角三角形 基础卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 27.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-06 00:00:00 | ||
图片预览

文档简介
湘教版八年级数学(下)第一章《直角三角形》基础卷(含答案)
一、选择题(30分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为(
)
A.
4
cm;
B.
2cm;
C.
1
cm;
D.
cm;
2、下列长度的三条线段能组成钝角三角形的是(
)
A.
3,4,4;
B.
3,4,5;
C.
3,4,6;
D.
3,4,7;
3、如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的实数为(
)
A.
2;
B.
;
C.
;
D.
;
4、如图,公路AC、BC互相垂直,公路AB的中点M于点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为(
)
A.
0.5km;
B.
0.6km;
C.
0.9km;
D.
1.2km;
5、已知一个直角三角形的两边长分别为3和4,则第三边的平方是(
)
A.
25;
B.
14;
C.
7;
D.
7或25;
6、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;
③∠A=90°-∠B;④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有(
)
A.
1个;
B.
2个;
C.
3个;
D.
4个;
7、如图,若BE⊥CD,BE=CD,BC=DA,则∠CFD
(
)
A.大于90°;
B.
等于90°;
C.
小于90°;
D.
不确定;
8、等边三角形的边长为2,则该三角形的面积为
(
)
A.
;
B.
;
C.
;
D.
3;
9、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是
AC的垂直平分线,DE交AB于点D,连接CD,则CD=(
)
A.
3;
B.
4;
C.4.8;
D.
5;
10、如图,分别以直角三角形的三边为边长向外作正方
形,然后分别以正方形的中心为圆心,正方形的边长
一半为半径作圆,记三个圆的面积分别为S1
,S2,
S3
则S1
,S2,
S3之间的关系是(
)
A.
S1+S2>S3;
B.
S1+S2=S3;
C.
S1+S2D.
无法确定;
二、填空题(24分)
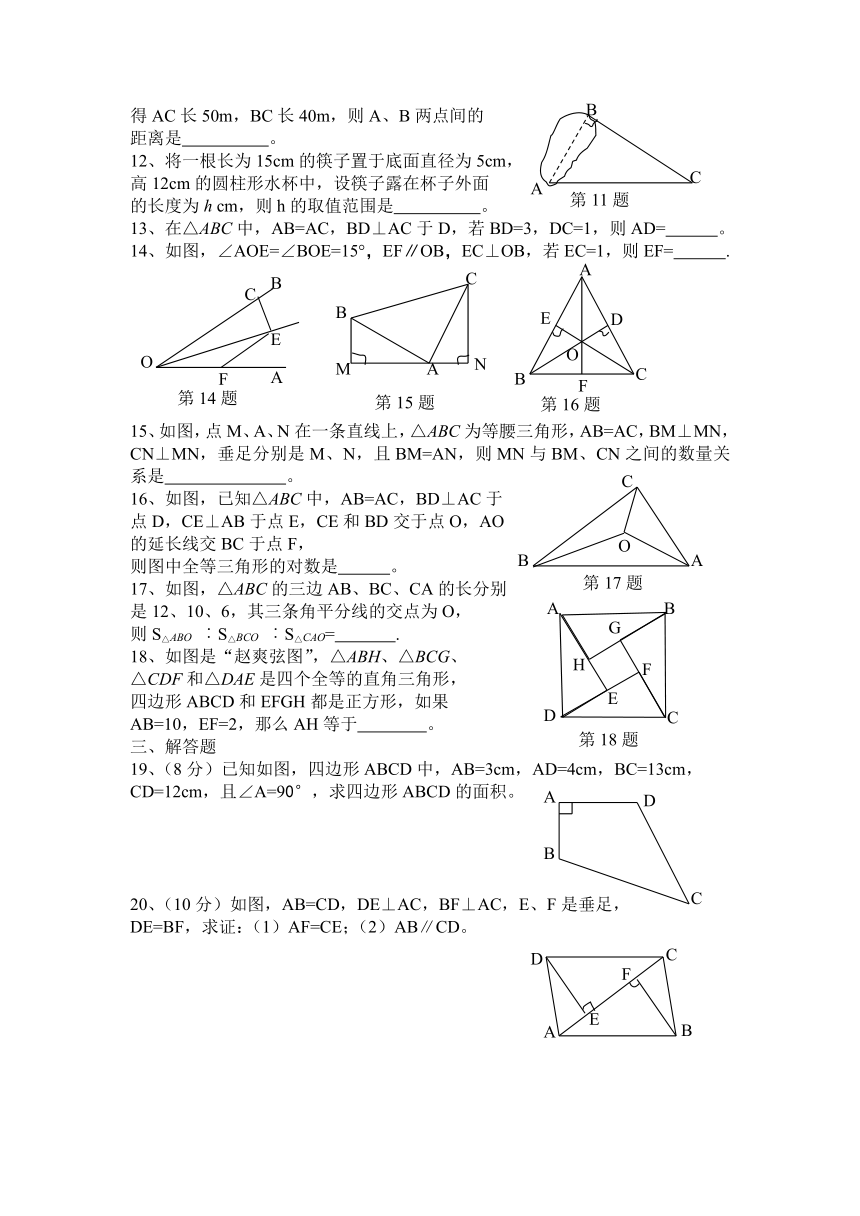
11、如图,为测得池塘两岸点A和点B间的距离,
一个观测者在C点设桩,使∠ABC=90°,并测
得AC长50m,BC长40m,则A、B两点间的
距离是
。
12、将一根长为15cm的筷子置于底面直径为5cm,
高12cm的圆柱形水杯中,设筷子露在杯子外面
的长度为h
cm,则h的取值范围是
。
13、在△ABC中,AB=AC,BD⊥AC于D,若BD=3,DC=1,则AD=
。
14、如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF=
.
15、如图,点M、A、N在一条直线上,△ABC为等腰三角形,AB=AC,BM⊥MN,
CN⊥MN,垂足分别是M、N,且BM=AN,则MN与BM、CN之间的数量关系是
。
16、如图,已知△ABC中,AB=AC,BD⊥AC于
点D,CE⊥AB于点E,CE和BD交于点O,AO
的延长线交BC于点F,
则图中全等三角形的对数是
。
17、如图,△ABC的三边AB、BC、CA的长分别
是12、10、6,其三条角平分线的交点为O,
则S△ABO
︰S△BCO
︰S△CAO=
.
18、如图是“赵爽弦图”,△ABH、△BCG、
△CDF和△DAE是四个全等的直角三角形,
四边形ABCD和EFGH都是正方形,如果
AB=10,EF=2,那么AH等于
。
三、解答题
19、(8分)已知如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,
CD=12cm,且∠A=90°,求四边形ABCD的面积。
20、(10分)如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,
DE=BF,求证:(1)AF=CE;(2)AB∥CD。
21、(10分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,
DB=9,(1)求CD的长;(2)求AB长;
22、(8分)“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h,
如图,一辆小汽车在一条城街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A点正前方30m处的C点,过了2s后,测得小汽车与车速检测仪间的距离为50m,这辆小汽车超速了吗?
23、(10分)如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,E、F是垂足,
AE=AF,求证:(1)PE=PF;(2)点P在∠BAC的角平分线上;
参考答案:
一、1、C;2、C;3、C;4、D;5、D;6、D;7、B;8、B;9、D;10、B;
二、11、30;12、;13、4;14、2;15、MN=BM+CN;
16、7对;17、6︰5︰3;18、6;
三、19、提示;连接BD,四边形ABCD的面积是36cm2;
20、(1)提示;证明:Rt△ABF≌Rt△CDE(HL);∴AF=CE;
(2)∵Rt△ABF≌Rt△CDE(HL);∴∠DCE=∠BAF,∴AB∥CD;
21、(1)CD=12;(2)AB=25;
22、由题意知AC=30m,AB=50m,∵AC⊥BC,
∴,∴BC=40m,
∴,这辆小汽车超速了。
23、证明:(1)连接AP并延长,∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,又∵AE=AF,AP=AP;
∴Rt△AEP≌Rt△AFP(HL);∴PE=PF;
(2)∵Rt△AEP≌Rt△AFP(HL);∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线;即:点P在∠BAC的角平分线上;
A
B
C
D
E
F
第7题
0
-1
1
A
B
C
D
M
第3题
A
B
C
M
第4题
A
B
C
D
E
第9题
S2
S3
S1
第10题
A
B
C
第11题
A
B
C
D
E
F
O
第16题
A
B
C
M
N
第15题
A
B
C
E
F
O
第14题
A
B
C
O
第17题
A
B
C
D
E
F
G
H
第18题
A
B
C
D
A
B
C
D
E
F
A
B
C
D
A
B
C
小汽车
小汽车
检测点
A
B
C
P
E
F
一、选择题(30分)
1、在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC的长为(
)
A.
4
cm;
B.
2cm;
C.
1
cm;
D.
cm;
2、下列长度的三条线段能组成钝角三角形的是(
)
A.
3,4,4;
B.
3,4,5;
C.
3,4,6;
D.
3,4,7;
3、如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的实数为(
)
A.
2;
B.
;
C.
;
D.
;
4、如图,公路AC、BC互相垂直,公路AB的中点M于点C被湖隔开,若测得AM的长为1.2km,则M,C两点间的距离为(
)
A.
0.5km;
B.
0.6km;
C.
0.9km;
D.
1.2km;
5、已知一个直角三角形的两边长分别为3和4,则第三边的平方是(
)
A.
25;
B.
14;
C.
7;
D.
7或25;
6、下列条件:①∠A+∠B=∠C;②∠A︰∠B︰∠C=1︰2︰3;
③∠A=90°-∠B;④∠A=∠B=∠C,其中能确定△ABC是直角三角形的条件有(
)
A.
1个;
B.
2个;
C.
3个;
D.
4个;
7、如图,若BE⊥CD,BE=CD,BC=DA,则∠CFD
(
)
A.大于90°;
B.
等于90°;
C.
小于90°;
D.
不确定;
8、等边三角形的边长为2,则该三角形的面积为
(
)
A.
;
B.
;
C.
;
D.
3;
9、如图,已知△ABC中,AB=10,AC=8,BC=6,DE是
AC的垂直平分线,DE交AB于点D,连接CD,则CD=(
)
A.
3;
B.
4;
C.4.8;
D.
5;
10、如图,分别以直角三角形的三边为边长向外作正方
形,然后分别以正方形的中心为圆心,正方形的边长
一半为半径作圆,记三个圆的面积分别为S1
,S2,
S3
则S1
,S2,
S3之间的关系是(
)
A.
S1+S2>S3;
B.
S1+S2=S3;
C.
S1+S2
无法确定;
二、填空题(24分)
11、如图,为测得池塘两岸点A和点B间的距离,
一个观测者在C点设桩,使∠ABC=90°,并测
得AC长50m,BC长40m,则A、B两点间的
距离是
。
12、将一根长为15cm的筷子置于底面直径为5cm,
高12cm的圆柱形水杯中,设筷子露在杯子外面
的长度为h
cm,则h的取值范围是
。
13、在△ABC中,AB=AC,BD⊥AC于D,若BD=3,DC=1,则AD=
。
14、如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF=
.
15、如图,点M、A、N在一条直线上,△ABC为等腰三角形,AB=AC,BM⊥MN,
CN⊥MN,垂足分别是M、N,且BM=AN,则MN与BM、CN之间的数量关系是
。
16、如图,已知△ABC中,AB=AC,BD⊥AC于
点D,CE⊥AB于点E,CE和BD交于点O,AO
的延长线交BC于点F,
则图中全等三角形的对数是
。
17、如图,△ABC的三边AB、BC、CA的长分别
是12、10、6,其三条角平分线的交点为O,
则S△ABO
︰S△BCO
︰S△CAO=
.
18、如图是“赵爽弦图”,△ABH、△BCG、
△CDF和△DAE是四个全等的直角三角形,
四边形ABCD和EFGH都是正方形,如果
AB=10,EF=2,那么AH等于
。
三、解答题
19、(8分)已知如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,
CD=12cm,且∠A=90°,求四边形ABCD的面积。
20、(10分)如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,
DE=BF,求证:(1)AF=CE;(2)AB∥CD。
21、(10分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,
DB=9,(1)求CD的长;(2)求AB长;
22、(8分)“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h,
如图,一辆小汽车在一条城街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A点正前方30m处的C点,过了2s后,测得小汽车与车速检测仪间的距离为50m,这辆小汽车超速了吗?
23、(10分)如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,E、F是垂足,
AE=AF,求证:(1)PE=PF;(2)点P在∠BAC的角平分线上;
参考答案:
一、1、C;2、C;3、C;4、D;5、D;6、D;7、B;8、B;9、D;10、B;
二、11、30;12、;13、4;14、2;15、MN=BM+CN;
16、7对;17、6︰5︰3;18、6;
三、19、提示;连接BD,四边形ABCD的面积是36cm2;
20、(1)提示;证明:Rt△ABF≌Rt△CDE(HL);∴AF=CE;
(2)∵Rt△ABF≌Rt△CDE(HL);∴∠DCE=∠BAF,∴AB∥CD;
21、(1)CD=12;(2)AB=25;
22、由题意知AC=30m,AB=50m,∵AC⊥BC,
∴,∴BC=40m,
∴,这辆小汽车超速了。
23、证明:(1)连接AP并延长,∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,又∵AE=AF,AP=AP;
∴Rt△AEP≌Rt△AFP(HL);∴PE=PF;
(2)∵Rt△AEP≌Rt△AFP(HL);∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线;即:点P在∠BAC的角平分线上;
A
B
C
D
E
F
第7题
0
-1
1
A
B
C
D
M
第3题
A
B
C
M
第4题
A
B
C
D
E
第9题
S2
S3
S1
第10题
A
B
C
第11题
A
B
C
D
E
F
O
第16题
A
B
C
M
N
第15题
A
B
C
E
F
O
第14题
A
B
C
O
第17题
A
B
C
D
E
F
G
H
第18题
A
B
C
D
A
B
C
D
E
F
A
B
C
D
A
B
C
小汽车
小汽车
检测点
A
B
C
P
E
F
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
