青岛版八年级第二学期期末检测试题(含答案)
文档属性
| 名称 | 青岛版八年级第二学期期末检测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 260.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-07 00:00:00 | ||
图片预览



文档简介
八年级数学第二学期期末学业检测试题
(时间120分钟,满分120分)
一、选择题(本题共12小题,在每小题给出
( http: / / www.21cnjy.com )的四个选项中,只有一个是正确的,请把正确的选项选出来填在第Ⅱ卷的表格里,每小题选对得3分,满分36分.
多选、不选、错选均记零分.)
1.
下列四幅图案在设计中用到平移变换方式的是(
)
( http: / / www.21cnjy.com )
2.
一元一次方程的解,函数的图象与轴的交点坐标为(
)
A.
(-3
,0)
B.
(3
,0)
C.(a
,0)
D.(-b
,0)
3.
计算的结果是(
)
A.
B.
C.-
D.
4.
下列计算正确的是(
)
A.
B.
C.
D.
5.已知一次函数,随着的增大而减小,且,则在直角坐标系内它的大致图象是(
)
6.
如图,矩形ABCD中,AB=3,AD
( http: / / www.21cnjy.com )=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数是(
)
A.2
B.
C.
D.
7.在如图所示的平面直角坐标系内,画在透明
( http: / / www.21cnjy.com )胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,﹣1)处,则此平移可以是( )
A.
先向右平移5个单位,再向下平移1个单位
B.
先向右平移5个单位,再向下平移3个单位
C.
先向右平移4个单位,再向下平移1个单位
D.
先向右平移4个单位,再向下平移3个单位
8.
下列二次根式是最简二次根式的是(
)
A.
B.
C.
D.
9.
在潍坊召开的出租汽车
( http: / / www.21cnjy.com )价格听证会上,物价局拟定了两套客运出租汽车运价调整方案,方案一,起步价调至7元/2公里,而后每公里1.6元(不足1公里,按1公里计算);方案二:起步价调至8元/3公里,而后每公里1.8元(不足1公里,按1公里计算),若某乘客乘坐出租车(路程多于3公里)时用方案一比较合算,则该乘客乘坐出租车的路程可能为(
)
A.
7公里
B.
5公里
C.
4公里
D.
3.5公里
10.
如图,是一台自动测温记录仪的图
( http: / / www.21cnjy.com )像,它反映了我市去年冬天某天气温T随时间t变化而变化的关系,观察图像得到下列信息,其中错误的是(
)
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时到14时,气温随时间增长而上升
D.从14时到24时,气温随时间增长而下降
11.不等式组的最小整数解是(
)
A.1
B.2
C.3
D.4
12.如图,四边形ABCD中,AD
( http: / / www.21cnjy.com )=BC,E、F、G分别是AB、DC、AC的中点,若∠ACB=64°,
∠DAC=22°,则∠EFG的度数为(
)
A.
42°
B.
38°
C.
32°
D.
21°
二、填空题(本题共6小题,
每小题3分,满分18分)
13.
一次函数的图像过,且随的增大而增大,则
.
14.如果点在第一象限,且为整数,则点的坐标为
.
15.
若二次根式有意义,则x的取值范围是
.
16.
在等腰三角形ABC中,,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为
.
17.
如图,函数和的图像相交于点A(m,3),则不等式的解集为
.
18.
如图,AB=4,BC=3,CD=13,AD=12,AB⊥BC,则四边形ABCD的面积是
.
三、解答题(本题共6小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.
(本题满分10分)
解关于x、y的方程组:
(1)为何值时,x、y都小于1;
(2)为何值时,大于0,小于2.
20.
(本题满分10分,每小题5分)
已知:,,求下列各式的值.
(1)
(2)
21.
(本题满分10分)
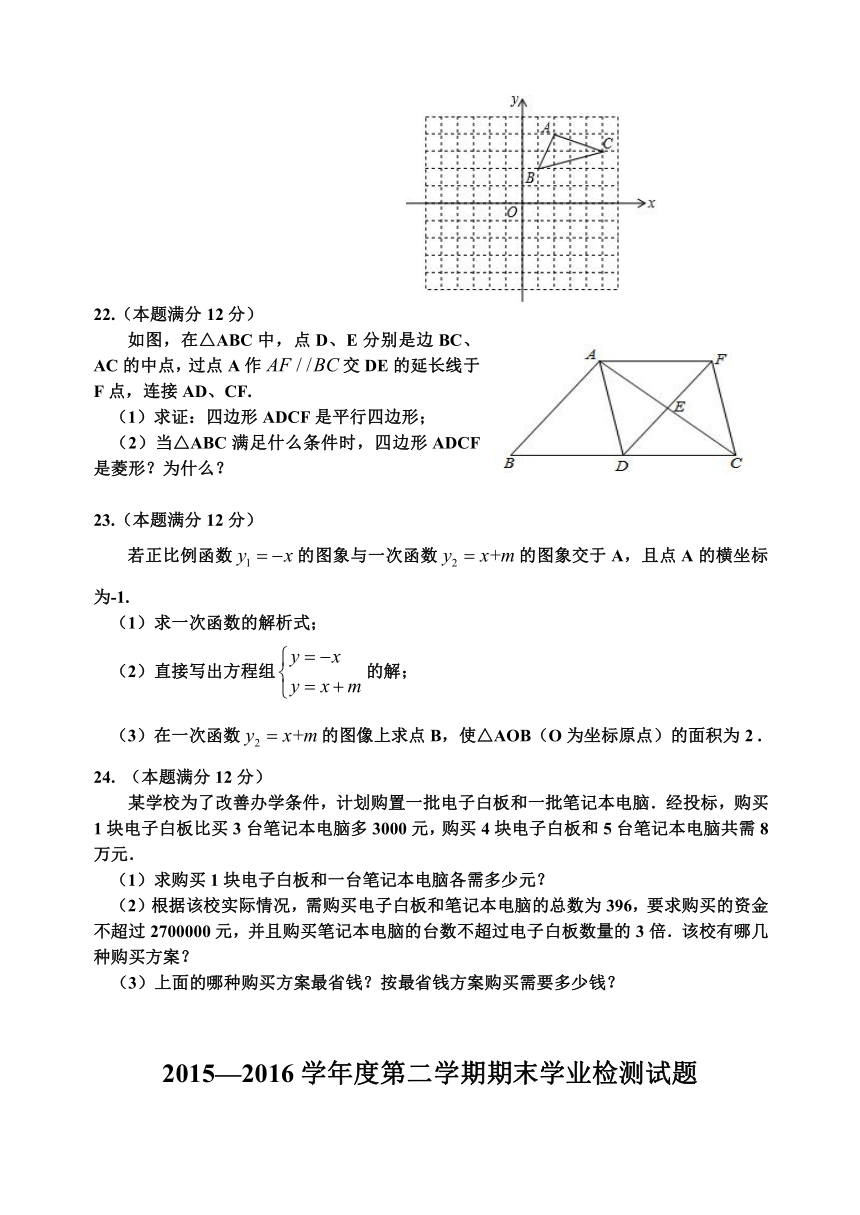
在平面直角坐标系中,△ABC的点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
(1)以点O(0,0)为旋转中心将
( http: / / www.21cnjy.com )△ABC顺时针转动90°,得到△A1B1C1,在坐标系中画出△A1B1C1,并直接写出A1,B1,C1点的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),请直接写出在△A1B1C1上对应点P1的坐标.
22.(本题满分12分)
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
23.(本题满分12分)
若正比例函数的图象与一次函数的图象交于A,且点A的横坐标为-1.
(1)求一次函数的解析式;
(2)直接写出方程组的解;
(3)在一次函数的图像上求点B,使△AOB(O为坐标原点)的面积为2
.
24.
(本题满分12分)
某学校为了改善办学条件,计划购置一批电子白板
( http: / / www.21cnjy.com )和一批笔记本电脑.经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需8万元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需
( http: / / www.21cnjy.com )购买电子白板和笔记本电脑的总数为396,要求购买的资金不超过2700000元,并且购买笔记本电脑的台数不超过电子白板数量的3倍.该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
2015—2016学年度第二学期期末学业检测试题
八年级数学答案及评分标准
一、选择题(共12个小题,每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
B
A
C
B
B
A
C
C
D
二、填空题(每题3分,共计18分)
13.2
14.
15.
x>
16.
17.
18.
36
三、解答题(本大题共计66分)
19.(本题满分10分,每小题5分)
解:解得……………………………………2分
(1)由已知的
即
解得
所以k<0
……6分
(2)由已知的
即
解得所以
……10分
(说明:根据步骤,酌情给分)
20.(本题满分10分)
(1)8
(2)
21.(本题满分10分)
解:(1)如图,△A1B
( http: / / www.21cnjy.com )1C1为所作,写出A1,B1,C1点的坐标分别为A1(4,-2),B1(2,-1),C1(3,-5);
……………3分
……………7分
(2)点P
(m,n)的对应点P1(n,-m).
……………10分
22.(本题满分12分)
(1)证明:∵点D
,E
分别是边BC
,AC的中点
∴DE//AB
∵AF//BC
∴四边形ABDF是平行四边形……………3分
∴AF=BD
又∵BD=DC
∴AF=DC
∵AF//BC
∴四边形ADCF是平行四边形
……………6分
(2)当AB⊥AC时,四边形ADCF是菱形
……………8分
理由:∵点D是边BC的中点,△ABC是直角三角形
∴AD=BC=DC
……………10分
又∵四边形ADCF是平行四边形
∴平行四边形ADCF是菱形
……………12分
23.(本题满分12分)
解:(1)将代入,得,则点A坐标为(-1,1)
将A(-1,1)代入,得,
所以此一函数的解析式为;
……………2分
(2)方程组的解为
……………4分
(3)设直线与y
轴的交点为C,与x轴的交点为D,则C(0,2),D(-2,0),
∵A(-1,1),
∴
①当B点在第一象限时,则,
设B点的横坐标为m,
∴,解得m=1,
∴B(1,3);
……………8分
②当B点在第三象限时,则,
设B点的横坐标为n,
∴,解得n=-1,
∴B(-3,-1);
……………12分
总上B点的坐标为(1,3)或(-3,-1)
24.(本大题满分12分)
解:(1)设购买一台笔记本电脑需x元,购买1块电子白板需y元,根据题意得
…………………………………………………………2分
解得x=4000,y=15000
……………………………………………………3分
所以购买一台笔记本电脑需4000元,购买1块电子白板和需15000元.
(2)设购买电子白板z台,所以笔记本电脑台数是(396-z)台,所以得出不等式组
…………………………………………5分
解得:
………………………………………………………………6分
∵z是正整数,∴z的正整数值是99、100、101,(396-z)的值分别是297、296、295,
∴该校有3种购买方案:
方案一:购买电子白板与电脑分别是99与297
方案二:购买电子白板与电脑分别是100与296
方案三:购买电子白板与电脑分别是101与295
……………………………………9分
(3)方法一:
直接判断最少的方案:上面的购买方案最省
( http: / / www.21cnjy.com )钱的方案是总数在396的情况下,购买电子白板最少的情况,因此是方案一:即是购买电子白板与电脑分别是99与297
最省钱方案购买需要钱数是:15000×99+4000×297=2673000(元)
………………12分
方法二:分别计算,比较数额大小;…………………………(计算各1分,共计3分)
方法三:运用一次函数性质,确定最少的方案
需要钱数P=15000z+4000(396-z)=11000z+1584000
∵11000>0,∴P随z的增大而增大
∴第一种方案当z=99时,P取最小值
即:P=11000×99+1584000=2673000(元)
…………………………………………12分
y
x
O
y
x
O
y
x
O
y
x
O
A
B
C
D
第10题图
第7题图
第6题图
第12题图
(时间120分钟,满分120分)
一、选择题(本题共12小题,在每小题给出
( http: / / www.21cnjy.com )的四个选项中,只有一个是正确的,请把正确的选项选出来填在第Ⅱ卷的表格里,每小题选对得3分,满分36分.
多选、不选、错选均记零分.)
1.
下列四幅图案在设计中用到平移变换方式的是(
)
( http: / / www.21cnjy.com )
2.
一元一次方程的解,函数的图象与轴的交点坐标为(
)
A.
(-3
,0)
B.
(3
,0)
C.(a
,0)
D.(-b
,0)
3.
计算的结果是(
)
A.
B.
C.-
D.
4.
下列计算正确的是(
)
A.
B.
C.
D.
5.已知一次函数,随着的增大而减小,且,则在直角坐标系内它的大致图象是(
)
6.
如图,矩形ABCD中,AB=3,AD
( http: / / www.21cnjy.com )=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数是(
)
A.2
B.
C.
D.
7.在如图所示的平面直角坐标系内,画在透明
( http: / / www.21cnjy.com )胶片上的平行四边形ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,﹣1)处,则此平移可以是( )
A.
先向右平移5个单位,再向下平移1个单位
B.
先向右平移5个单位,再向下平移3个单位
C.
先向右平移4个单位,再向下平移1个单位
D.
先向右平移4个单位,再向下平移3个单位
8.
下列二次根式是最简二次根式的是(
)
A.
B.
C.
D.
9.
在潍坊召开的出租汽车
( http: / / www.21cnjy.com )价格听证会上,物价局拟定了两套客运出租汽车运价调整方案,方案一,起步价调至7元/2公里,而后每公里1.6元(不足1公里,按1公里计算);方案二:起步价调至8元/3公里,而后每公里1.8元(不足1公里,按1公里计算),若某乘客乘坐出租车(路程多于3公里)时用方案一比较合算,则该乘客乘坐出租车的路程可能为(
)
A.
7公里
B.
5公里
C.
4公里
D.
3.5公里
10.
如图,是一台自动测温记录仪的图
( http: / / www.21cnjy.com )像,它反映了我市去年冬天某天气温T随时间t变化而变化的关系,观察图像得到下列信息,其中错误的是(
)
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时到14时,气温随时间增长而上升
D.从14时到24时,气温随时间增长而下降
11.不等式组的最小整数解是(
)
A.1
B.2
C.3
D.4
12.如图,四边形ABCD中,AD
( http: / / www.21cnjy.com )=BC,E、F、G分别是AB、DC、AC的中点,若∠ACB=64°,
∠DAC=22°,则∠EFG的度数为(
)
A.
42°
B.
38°
C.
32°
D.
21°
二、填空题(本题共6小题,
每小题3分,满分18分)
13.
一次函数的图像过,且随的增大而增大,则
.
14.如果点在第一象限,且为整数,则点的坐标为
.
15.
若二次根式有意义,则x的取值范围是
.
16.
在等腰三角形ABC中,,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为
.
17.
如图,函数和的图像相交于点A(m,3),则不等式的解集为
.
18.
如图,AB=4,BC=3,CD=13,AD=12,AB⊥BC,则四边形ABCD的面积是
.
三、解答题(本题共6小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.
(本题满分10分)
解关于x、y的方程组:
(1)为何值时,x、y都小于1;
(2)为何值时,大于0,小于2.
20.
(本题满分10分,每小题5分)
已知:,,求下列各式的值.
(1)
(2)
21.
(本题满分10分)
在平面直角坐标系中,△ABC的点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
(1)以点O(0,0)为旋转中心将
( http: / / www.21cnjy.com )△ABC顺时针转动90°,得到△A1B1C1,在坐标系中画出△A1B1C1,并直接写出A1,B1,C1点的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),请直接写出在△A1B1C1上对应点P1的坐标.
22.(本题满分12分)
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
23.(本题满分12分)
若正比例函数的图象与一次函数的图象交于A,且点A的横坐标为-1.
(1)求一次函数的解析式;
(2)直接写出方程组的解;
(3)在一次函数的图像上求点B,使△AOB(O为坐标原点)的面积为2
.
24.
(本题满分12分)
某学校为了改善办学条件,计划购置一批电子白板
( http: / / www.21cnjy.com )和一批笔记本电脑.经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需8万元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需
( http: / / www.21cnjy.com )购买电子白板和笔记本电脑的总数为396,要求购买的资金不超过2700000元,并且购买笔记本电脑的台数不超过电子白板数量的3倍.该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
2015—2016学年度第二学期期末学业检测试题
八年级数学答案及评分标准
一、选择题(共12个小题,每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
B
A
C
B
B
A
C
C
D
二、填空题(每题3分,共计18分)
13.2
14.
15.
x>
16.
17.
18.
36
三、解答题(本大题共计66分)
19.(本题满分10分,每小题5分)
解:解得……………………………………2分
(1)由已知的
即
解得
所以k<0
……6分
(2)由已知的
即
解得所以
……10分
(说明:根据步骤,酌情给分)
20.(本题满分10分)
(1)8
(2)
21.(本题满分10分)
解:(1)如图,△A1B
( http: / / www.21cnjy.com )1C1为所作,写出A1,B1,C1点的坐标分别为A1(4,-2),B1(2,-1),C1(3,-5);
……………3分
……………7分
(2)点P
(m,n)的对应点P1(n,-m).
……………10分
22.(本题满分12分)
(1)证明:∵点D
,E
分别是边BC
,AC的中点
∴DE//AB
∵AF//BC
∴四边形ABDF是平行四边形……………3分
∴AF=BD
又∵BD=DC
∴AF=DC
∵AF//BC
∴四边形ADCF是平行四边形
……………6分
(2)当AB⊥AC时,四边形ADCF是菱形
……………8分
理由:∵点D是边BC的中点,△ABC是直角三角形
∴AD=BC=DC
……………10分
又∵四边形ADCF是平行四边形
∴平行四边形ADCF是菱形
……………12分
23.(本题满分12分)
解:(1)将代入,得,则点A坐标为(-1,1)
将A(-1,1)代入,得,
所以此一函数的解析式为;
……………2分
(2)方程组的解为
……………4分
(3)设直线与y
轴的交点为C,与x轴的交点为D,则C(0,2),D(-2,0),
∵A(-1,1),
∴
①当B点在第一象限时,则,
设B点的横坐标为m,
∴,解得m=1,
∴B(1,3);
……………8分
②当B点在第三象限时,则,
设B点的横坐标为n,
∴,解得n=-1,
∴B(-3,-1);
……………12分
总上B点的坐标为(1,3)或(-3,-1)
24.(本大题满分12分)
解:(1)设购买一台笔记本电脑需x元,购买1块电子白板需y元,根据题意得
…………………………………………………………2分
解得x=4000,y=15000
……………………………………………………3分
所以购买一台笔记本电脑需4000元,购买1块电子白板和需15000元.
(2)设购买电子白板z台,所以笔记本电脑台数是(396-z)台,所以得出不等式组
…………………………………………5分
解得:
………………………………………………………………6分
∵z是正整数,∴z的正整数值是99、100、101,(396-z)的值分别是297、296、295,
∴该校有3种购买方案:
方案一:购买电子白板与电脑分别是99与297
方案二:购买电子白板与电脑分别是100与296
方案三:购买电子白板与电脑分别是101与295
……………………………………9分
(3)方法一:
直接判断最少的方案:上面的购买方案最省
( http: / / www.21cnjy.com )钱的方案是总数在396的情况下,购买电子白板最少的情况,因此是方案一:即是购买电子白板与电脑分别是99与297
最省钱方案购买需要钱数是:15000×99+4000×297=2673000(元)
………………12分
方法二:分别计算,比较数额大小;…………………………(计算各1分,共计3分)
方法三:运用一次函数性质,确定最少的方案
需要钱数P=15000z+4000(396-z)=11000z+1584000
∵11000>0,∴P随z的增大而增大
∴第一种方案当z=99时,P取最小值
即:P=11000×99+1584000=2673000(元)
…………………………………………12分
y
x
O
y
x
O
y
x
O
y
x
O
A
B
C
D
第10题图
第7题图
第6题图
第12题图
同课章节目录
