18.2勾股定理的逆定理同步练习
图片预览




文档简介
沪科版八年级下册数学18.2勾股定理的逆定理同步练习
一、选择题(本大题共8小题)
1.分以下各组数为三角形的三条边长,其中能作成直角三角形的是( )
A.2,3,4 B.4,5,6 C.1,, D.2,,4
2. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )【来源:21·世纪·教育·网】
A.∠A:∠B:∠C=3:4:5 B.a:b:c=5:12:13
C.a2=b2﹣c2 D.∠A=∠C﹣∠B
3. 如图,在4×3的长方形网格中,已知A、B两点为格点(网格线的交点称为格点),若C也为该网格中的格点,且△ABC为等腰直角三角形,则格点C的个数为 .
A.5 B.6 C.3 D.4
4. 在△ABC中,∠B=30°,AB=12,AC的长度可以在6,24,4,2中取值,则满足上述条件的直角三角形有( )【出处:21教育名师】
A.1个 B.2个 C.3个 D.4个
5. 直角三角形的两直角边分别为5cm,12cm,其斜边上的高为( )
A.6cm B.8.5cm C. cm D. cm
6. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
7. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.【版权所有:21教育】
A.54 B.108 C.216 D.270
8. 已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
二、填空题(本大题共6小题)
9. 如图,△ABC中,AD=8,AC=10,DC=6,AB=17,则AC的长是 .
10. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
11. 已知两线段长分别为6cm,10cm,则当第三条线段长为 cm时,这三条线段能组成直角三角形.21教育名师原创作品
12. 已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,则BC的长为 .
13. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是 .21世纪教育网版权所有
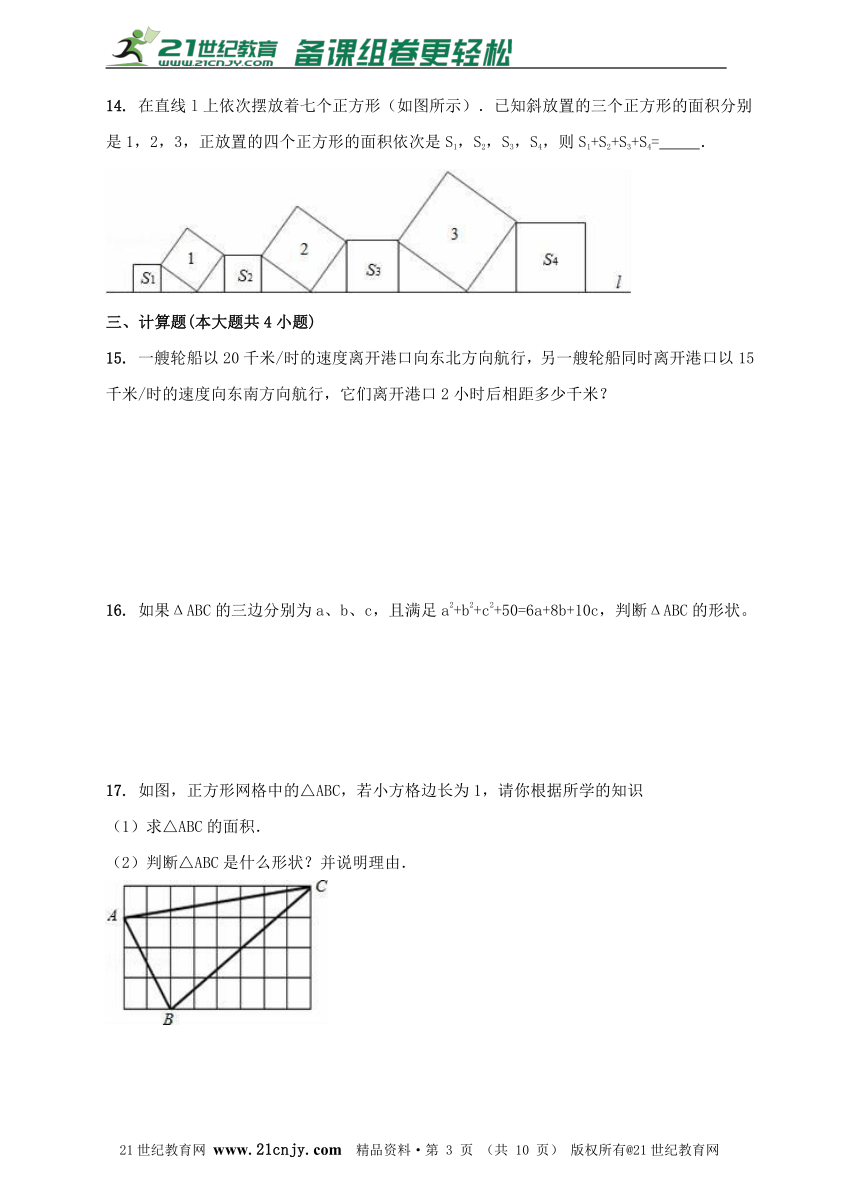
14. 在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .
三、计算题(本大题共4小题)
15. 一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
16. 如果ΔABC的三边分别为a、b、c,且满足a2+b2+c2+50=6a+8b+10c,判断ΔABC的形状。
17. 如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
(1)求△ABC的面积.
(2)判断△ABC是什么形状?并说明理由.
18. 如图3中的(1)是用硬纸板做成的形状大小完全相同的直角三角形,两直角边的长分别为a和b,斜边长为c;如图3中(2)是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明出勾股定理的图形.【来源:21cnj*y.co*m】
(1)画出拼成的这个图形的示意图,写出它是什么图形.
(2)用这个图形推出a2+b2=c2.(勾股定理)
(3)假设图中的(1)中的直角三角形有若干个,你能运用图中的(1)所给的直角三角形拼出另一种能推出a2+b2=c2的图形吗?请画出拼后的示意图.(无需证明)
参考答案:
一、选择题(本大题共8小题)
1.C
分析:由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解:A、22+32=13≠42=16,故A选项错误;
B、42+52=41≠62=36,故B选项错误;
C、12+()2=3=()2,此三角形是直角三角形,故C选项正确;
D、22+()2=6≠42=16,故D选项错误.
故选:C.
2. A
分析:利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解:A、∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,可求得∠C≠90°,故△ABC不是直角三角形;www.21-cn-jy.com
B、不妨设a=5,b=12,c=13,此时a2+b2=132=c2,即a2+b2=c2,故△ABC是直角三角形;
C、由条件可得到a2+c2=b2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC是直角三角形;
故选A.
3. B
分析:根据等腰直角三角形的判定和长方形网格的特点易作出满足条件的C点.
解:如图: 故6个.
4. B
分析:当∠A=90°,求得AC=4,当∠C=90°,求得AC=6,于是得到结论.
解:当∠A=90°,
∵∠B=30°,AB=12,
∴AC=4,
当∠C=90°,
∵∠B=30°,AB=12,
∴AC=6,
∴满足上述条件的直角三角形有2个,
故选B.
5. D
分析:先根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
解:∵直角三角形的两条直角边分别为5cm,12cm,
∴斜边==13cm,
设斜边上的高为h,则直角三角形的面积=×5×12=×13?h,
∴h=cm.
故选D.
6. A
分析:仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.21·cn·jy·com
【解答】解:梯脚与墙角距离: =0.7(米).
故选A.
7.C
分析:连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差.www-2-1-cnjy-com
解:连接AC,则在Rt△ADC中,
AC2=CD2+AD2=122+92=225,
∴AC=15,在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC﹣S△ACD=AC?BC﹣AD?CD=×15×36﹣×12×9=270﹣54=216.
答:这块地的面积是216平方米.
故选项为C。
8. D
分析:首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.21教育网
解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选D.
二、填空题(本大题共6小题)
9. 分析:先根据勾股定理的逆定理证明△ACD是直角三角形,再由勾股定理可以求得BD的长度,再根据线段的和差关系即可求解.21cnjy.com
解:∵AD2+CD2=82+62=102=AC2,
∴△ACD是直角三角形,
∴AD⊥BC,
在Rt△ABD中,BD==15,
BC=BD+CD=15+6=21,.
故答案为:21.
10. 分析:直接利用勾股定理得出AB的长,再利用AC+BC﹣AB进而得出答案.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
11. 分析:已知直角三角形的二边求第三边时,一定区分所求边是直角三角形斜边和短边二种情况下的结果.2-1-c-n-j-y
解:根据勾股定理,当10cm和6cm都为直角边时,第三条线段长为==2cm;
当10cm为斜边,6cm为直角边时,第三条线段长为=8cm,
故答案为:8或2.
12.分析:利用勾股定理的逆定理判断出△ABC为直角三角形,在直角三角形ABC中,由勾股定理求出CB即可.
解:因为△ABD中,∠ABD=90°,∠DAB=30°
所以BD= AD 又AD=12
所以BD=6 则AB=6
因为C=90°,所以三角形ABC是直角三角形
在直角三角形ABC中,AC=BC AB=6
所以=54,则 BC=3
13.分析:利用勾股定理的逆定理进行验证分析即可得到。
设小正方形的边长为1,
则AB 2=22+22=8,CD 2=22+42=20,EF 2=12+22=5,GH 2=22+32=13.21*cnjy*com
因为AB 2+EF 2=GH 2,所以能构成一个直角三角形三边的线段是AB、EF、GH.
14. 分析:运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=1,
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
故答案为:4.
三、计算题(本大题共4小题)
15. 分析:结合实际意境作图并构造直角三角形解答即可。
解:如图所示,直角三角形的两条直角边分别是OA=20×=40km,OB=15×2=30km.
再根据勾股定理,得两条船相距AB= =50km.
16. 分析:要判断ΔABC的形状,需要找到a、b、c的关系,而题目中只有条件a2+b2+c2+50=6a+8b+10c,故只有从该条件入手,解决问题。21·世纪*教育网
解:由a2+b2+c2+50=6a+8b+10c,得 :
a2-6a+9+b2-8b+16+c2-10c+25=0,
∴ (a-3)2+(b-4)2+(c-5)2=0。
∵ (a-3)2≥0, (b-4)2≥0, (c-5)2≥0。
∴ a=3,b=4,c=5。
∵ 32+42=52,
∴ a2+b2=c2。
由勾股定理的逆定理,得ΔABC是直角三角形。 17. 分析:(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解:(1)△ABC的面积=4×8﹣1×8÷2﹣2×3÷2﹣6×4÷2=13.
故△ABC的面积为13;
(2)∵正方形小方格边长为1
∴AC==,AB==,BC==2,
∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.
18. 解:(1)如图所示,是梯形;
(2)由上图我们根据梯形的面积公式可知,梯形的面积=(a+b)(a+b). 从上图我们还发现梯形的面积=三个三角形的面积,2·1·c·n·j·y
即++c2.两者列成等式化简即可得:a2+b2=c2;
(3)画边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边.
一、选择题(本大题共8小题)
1.分以下各组数为三角形的三条边长,其中能作成直角三角形的是( )
A.2,3,4 B.4,5,6 C.1,, D.2,,4
2. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )【来源:21·世纪·教育·网】
A.∠A:∠B:∠C=3:4:5 B.a:b:c=5:12:13
C.a2=b2﹣c2 D.∠A=∠C﹣∠B
3. 如图,在4×3的长方形网格中,已知A、B两点为格点(网格线的交点称为格点),若C也为该网格中的格点,且△ABC为等腰直角三角形,则格点C的个数为 .
A.5 B.6 C.3 D.4
4. 在△ABC中,∠B=30°,AB=12,AC的长度可以在6,24,4,2中取值,则满足上述条件的直角三角形有( )【出处:21教育名师】
A.1个 B.2个 C.3个 D.4个
5. 直角三角形的两直角边分别为5cm,12cm,其斜边上的高为( )
A.6cm B.8.5cm C. cm D. cm
6. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米 B.0.8米 C.0.9米 D.1.0米
7. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积S为( )cm2.【版权所有:21教育】
A.54 B.108 C.216 D.270
8. 已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是( )
A.底与腰不相等的等腰三角形 B.等边三角形
C.钝角三角形 D.直角三角形
二、填空题(本大题共6小题)
9. 如图,△ABC中,AD=8,AC=10,DC=6,AB=17,则AC的长是 .
10. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
11. 已知两线段长分别为6cm,10cm,则当第三条线段长为 cm时,这三条线段能组成直角三角形.21教育名师原创作品
12. 已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,则BC的长为 .
13. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是 .21世纪教育网版权所有
14. 在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .
三、计算题(本大题共4小题)
15. 一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
16. 如果ΔABC的三边分别为a、b、c,且满足a2+b2+c2+50=6a+8b+10c,判断ΔABC的形状。
17. 如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
(1)求△ABC的面积.
(2)判断△ABC是什么形状?并说明理由.
18. 如图3中的(1)是用硬纸板做成的形状大小完全相同的直角三角形,两直角边的长分别为a和b,斜边长为c;如图3中(2)是以c为直角边的等腰直角三角形,请你开动脑筋,将它们拼成一个能证明出勾股定理的图形.【来源:21cnj*y.co*m】
(1)画出拼成的这个图形的示意图,写出它是什么图形.
(2)用这个图形推出a2+b2=c2.(勾股定理)
(3)假设图中的(1)中的直角三角形有若干个,你能运用图中的(1)所给的直角三角形拼出另一种能推出a2+b2=c2的图形吗?请画出拼后的示意图.(无需证明)
参考答案:
一、选择题(本大题共8小题)
1.C
分析:由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解:A、22+32=13≠42=16,故A选项错误;
B、42+52=41≠62=36,故B选项错误;
C、12+()2=3=()2,此三角形是直角三角形,故C选项正确;
D、22+()2=6≠42=16,故D选项错误.
故选:C.
2. A
分析:利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解:A、∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,可求得∠C≠90°,故△ABC不是直角三角形;www.21-cn-jy.com
B、不妨设a=5,b=12,c=13,此时a2+b2=132=c2,即a2+b2=c2,故△ABC是直角三角形;
C、由条件可得到a2+c2=b2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC是直角三角形;
故选A.
3. B
分析:根据等腰直角三角形的判定和长方形网格的特点易作出满足条件的C点.
解:如图: 故6个.
4. B
分析:当∠A=90°,求得AC=4,当∠C=90°,求得AC=6,于是得到结论.
解:当∠A=90°,
∵∠B=30°,AB=12,
∴AC=4,
当∠C=90°,
∵∠B=30°,AB=12,
∴AC=6,
∴满足上述条件的直角三角形有2个,
故选B.
5. D
分析:先根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
解:∵直角三角形的两条直角边分别为5cm,12cm,
∴斜边==13cm,
设斜边上的高为h,则直角三角形的面积=×5×12=×13?h,
∴h=cm.
故选D.
6. A
分析:仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.21·cn·jy·com
【解答】解:梯脚与墙角距离: =0.7(米).
故选A.
7.C
分析:连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差.www-2-1-cnjy-com
解:连接AC,则在Rt△ADC中,
AC2=CD2+AD2=122+92=225,
∴AC=15,在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC﹣S△ACD=AC?BC﹣AD?CD=×15×36﹣×12×9=270﹣54=216.
答:这块地的面积是216平方米.
故选项为C。
8. D
分析:首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.21教育网
解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选D.
二、填空题(本大题共6小题)
9. 分析:先根据勾股定理的逆定理证明△ACD是直角三角形,再由勾股定理可以求得BD的长度,再根据线段的和差关系即可求解.21cnjy.com
解:∵AD2+CD2=82+62=102=AC2,
∴△ACD是直角三角形,
∴AD⊥BC,
在Rt△ABD中,BD==15,
BC=BD+CD=15+6=21,.
故答案为:21.
10. 分析:直接利用勾股定理得出AB的长,再利用AC+BC﹣AB进而得出答案.
解:由题意可得:AB==10(m),
则AC+BC﹣AB=14﹣10=4(m),
故他们仅仅少走了:4×2=8(步).
故答案为:8.
11. 分析:已知直角三角形的二边求第三边时,一定区分所求边是直角三角形斜边和短边二种情况下的结果.2-1-c-n-j-y
解:根据勾股定理,当10cm和6cm都为直角边时,第三条线段长为==2cm;
当10cm为斜边,6cm为直角边时,第三条线段长为=8cm,
故答案为:8或2.
12.分析:利用勾股定理的逆定理判断出△ABC为直角三角形,在直角三角形ABC中,由勾股定理求出CB即可.
解:因为△ABD中,∠ABD=90°,∠DAB=30°
所以BD= AD 又AD=12
所以BD=6 则AB=6
因为C=90°,所以三角形ABC是直角三角形
在直角三角形ABC中,AC=BC AB=6
所以=54,则 BC=3
13.分析:利用勾股定理的逆定理进行验证分析即可得到。
设小正方形的边长为1,
则AB 2=22+22=8,CD 2=22+42=20,EF 2=12+22=5,GH 2=22+32=13.21*cnjy*com
因为AB 2+EF 2=GH 2,所以能构成一个直角三角形三边的线段是AB、EF、GH.
14. 分析:运用勾股定理可知,每两个相邻的正方形面积和都等于中间斜放的正方形面积,据此即可解答.
解:观察发现,
∵AB=BE,∠ACB=∠BDE=90°,
∴∠ABC+∠BAC=90°,∠ABC+∠EBD=90°,
∴∠BAC=∠EBD,
∴△ABC≌△BDE(AAS),
∴BC=ED,
∵AB2=AC2+BC2,
∴AB2=AC2+ED2=S1+S2,
即S1+S2=1,
同理S3+S4=3.
则S1+S2+S3+S4=1+3=4.
故答案为:4.
三、计算题(本大题共4小题)
15. 分析:结合实际意境作图并构造直角三角形解答即可。
解:如图所示,直角三角形的两条直角边分别是OA=20×=40km,OB=15×2=30km.
再根据勾股定理,得两条船相距AB= =50km.
16. 分析:要判断ΔABC的形状,需要找到a、b、c的关系,而题目中只有条件a2+b2+c2+50=6a+8b+10c,故只有从该条件入手,解决问题。21·世纪*教育网
解:由a2+b2+c2+50=6a+8b+10c,得 :
a2-6a+9+b2-8b+16+c2-10c+25=0,
∴ (a-3)2+(b-4)2+(c-5)2=0。
∵ (a-3)2≥0, (b-4)2≥0, (c-5)2≥0。
∴ a=3,b=4,c=5。
∵ 32+42=52,
∴ a2+b2=c2。
由勾股定理的逆定理,得ΔABC是直角三角形。 17. 分析:(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解:(1)△ABC的面积=4×8﹣1×8÷2﹣2×3÷2﹣6×4÷2=13.
故△ABC的面积为13;
(2)∵正方形小方格边长为1
∴AC==,AB==,BC==2,
∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.
18. 解:(1)如图所示,是梯形;
(2)由上图我们根据梯形的面积公式可知,梯形的面积=(a+b)(a+b). 从上图我们还发现梯形的面积=三个三角形的面积,2·1·c·n·j·y
即++c2.两者列成等式化简即可得:a2+b2=c2;
(3)画边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边.
