7.3.1一元一次不等式组同步练习
图片预览

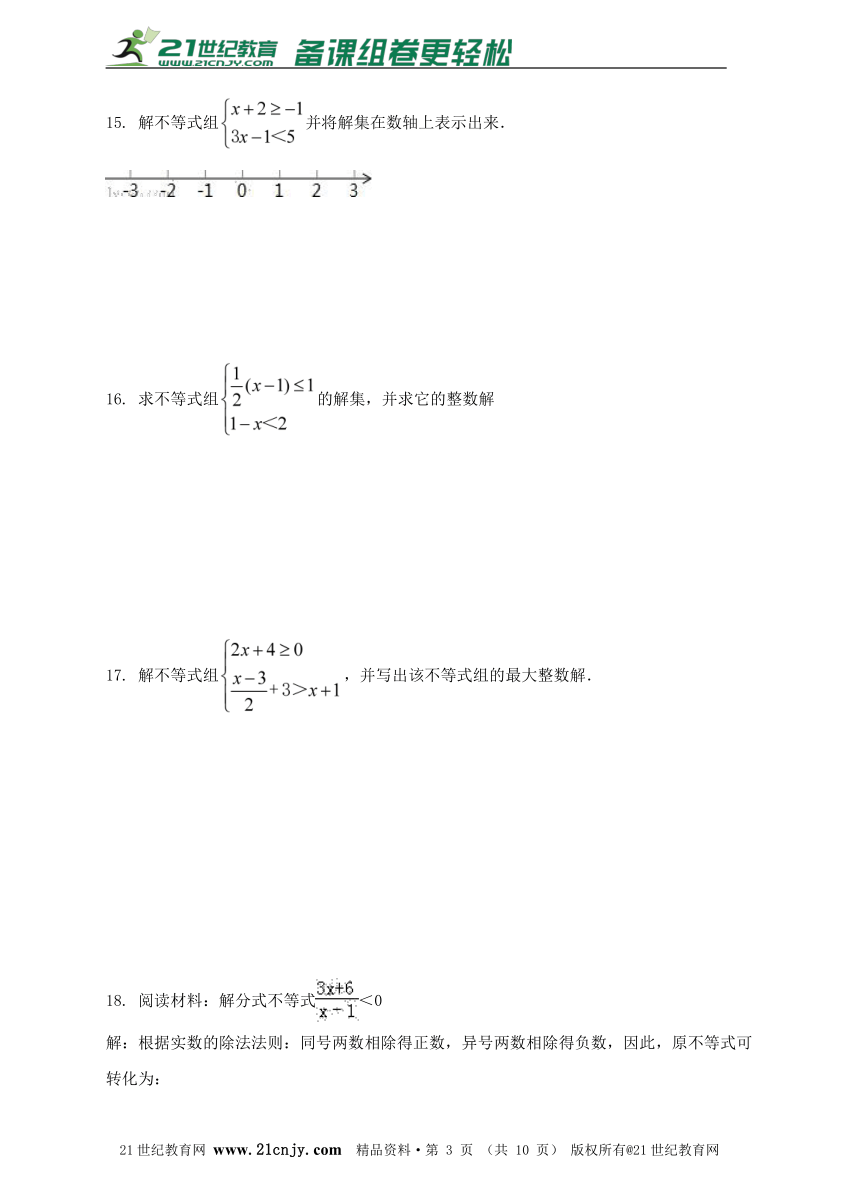


文档简介
沪科版七年级下册数学7.3.1一元一次不等式组同步练习
一、选择题(本大题共8小题)
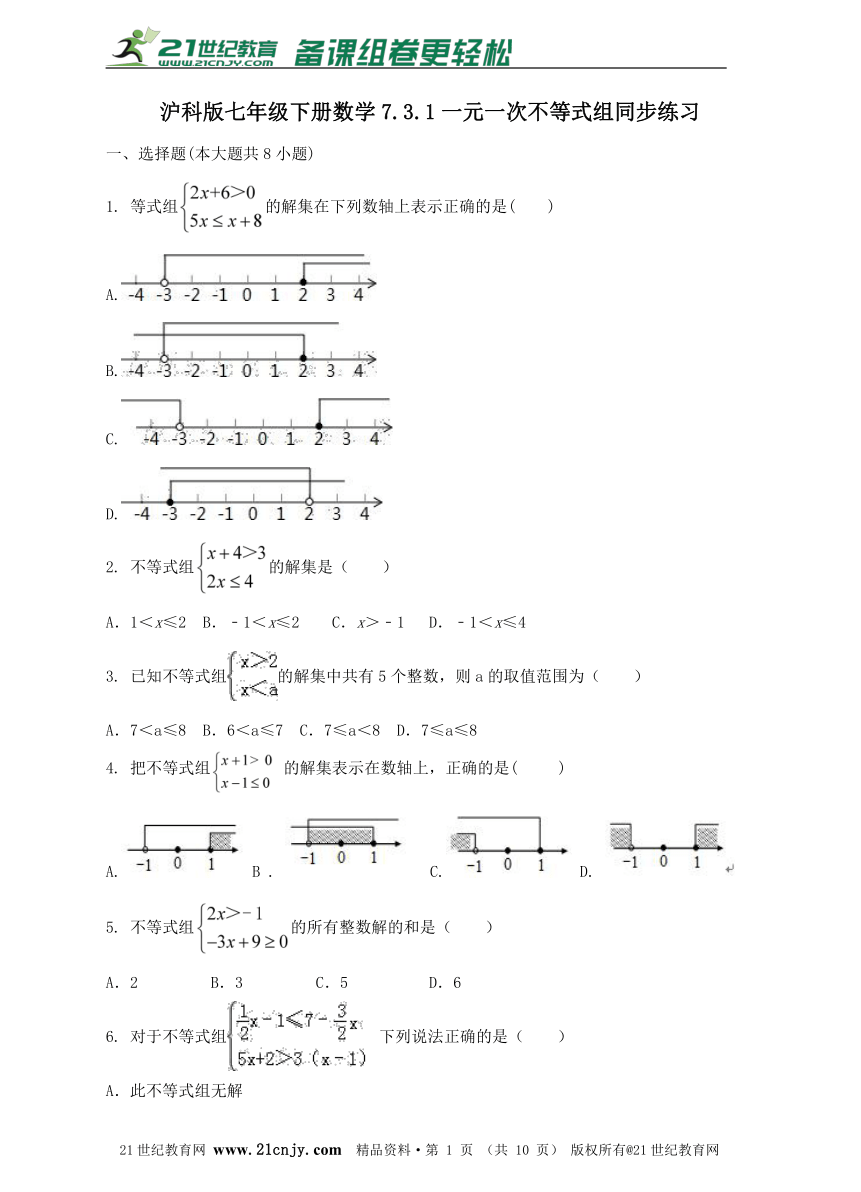
1. 等式组的解集在下列数轴上表示正确的是( )
A.
B.
C.
D.
2. 不等式组的解集是( )
A.1<x≤2 B.﹣1<x≤2 C.x>﹣1 D.﹣1<x≤4
3. 已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
4. 把不等式组的解集表示在数轴上,正确的是( )
A.B . C. D.
5. 不等式组的所有整数解的和是( )
A.2 B.3 C.5 D.6
6. 对于不等式组下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣<x≤2
7. 小亮在解不等式组时,解法步骤如下:
解不等式①,得x>3,…第一步;
解不等式②,得x>﹣8,…第二步;
所有原不等式组组的解集为﹣8<x<3…第三步.
对于以上解答,你认为下列判断正确的是( )
A.解答有误,错在第一步 B.解答有误,错在第二步
C.解答有误,错在第三步 D.原解答正确无误
8. △ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A.4 B.4或5 C.5或6 D.6
二、填空题(本大题共6小题)
9. 关于x的不等式组的解集是_____.
10. 不等式组的所有整数解是 .
11. 不等式组的所有整数解的积为 .
12. 若不等式组有解,则a的取值范围是 .
13. 对于任意实数m、n,定义一种运运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是 .21教育网
14. 已知关于x、y的方程组的解是一对异号的数,则k的取值范围是_____.
三、计算题(本大题共4小题)
15. 解不等式组并将解集在数轴上表示出来.
16. 求不等式组的解集,并求它的整数解
17. 解不等式组,并写出该不等式组的最大整数解.
18. 阅读材料:解分式不等式<0
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:无解,解②得:﹣2<x<1
所以原不等式的解集是﹣2<x<1
请仿照上述方法解下列分式不等式:
(1)≤0
(2)>0.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:本题应该先对不等式组进行化简,然后在数轴上分别表示出x的取值范围,它们的公共部分就是不等式组的解集.21世纪教育网版权所有
解:不等式可化为:.
在数轴上表示为: 故选B.
2. B
分析:分别解两个不等式得到x>﹣1和x≤2,然后根据大小小大中间找确定不等数组的解集.
解: ,
解①得x>﹣1,
解②得x≤2,
所以不等式组的解集为﹣1<x≤2.
故选B.
3. A
分析:根据不等式组的解集中共有5个整数解,求出a的范围即可.
解:∵不等式组的解集中共有5个整数,
∴a的范围为7<a≤8,故选A.
4. B
分析:先根据不等式组解答得出x的范围再在数轴上进行标记即可。
解:
解不等式(1)得x>-1,
解不等式(2)得x≤1,
所以解集为-1故选B
5.D
分析:先求出不等式组的解集,再求出不等式组的整数解,最后求出答案即可.
解:
∵解不等式①得;x>﹣,
解不等式②得;x≤3,
∴不等式组的解集为﹣<x≤3,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
6.B
分析:分别解两个不等式得到x≤4和x>﹣2.5,利用大于小的小于大的取中间可确定不等式组的解集,再写出不等式组的整数解,然后对各选项进行判断.21·cn·jy·com
解::,
解①得x≤4,
解②得x>﹣2.5,
所以不等式组的解集为﹣2.5<x≤4,
所以不等式组的整数解为﹣2,﹣1,0,1,2,3,4.
故选B.
7. A
分析:先计算出每个不等式的解集,再根据过程进行判断。
解:解不等式①,得x>3,
解不等式②,得x>﹣8,
所以原不等式组的解集为x>3.
故选C.
8. B
分析:先设长度为4、12的高分别是a、b边上的,边c上的高为h,△ABC的面积是S,根据三角形面积公式,可求a=,b=,c=,结合三角形三边的不等关系,可得关于h的不等式,解即可.21cnjy.com
解:设长度为4、12的高分别是a,b边上的,边c上的高为h,△ABC的面积是S,那么
a=,b=,c=,
又∵a﹣b<c<a+b,
∴﹣<c<+,
即<<S,
解得3<h<6,
∴h=4或h=5,故选B.
二、填空题(本大题共6小题)
9. 分析:分别求出每个不等式的解集,再求其解集的公共部分即可.
解: 由①得,x≥2, 由②得,x>4, 根据“同大取较大”原则,原不等式组的解集为x>4.
10.分析:先求出两个不等式的解集,再求其公共解,然后写出范围内的整数即可.
解:,
解不等式①得,x>﹣,
解不等式②得,x≤1,
所以不等式组的解集为﹣x≤1,
所以原不等式组的整数解是0,1.
故答案为:0,1.
11.分析:先分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的所有整数解相乘即可求解.www.21-cn-jy.com
解:,
解不等式①得:x,
解不等式②得:x≤50,
∴不等式组的整数解为﹣1,0,1…50,
所以所有整数解的积为0,
故答案为:0.
12.分析:先把x当作已知条件得出不等式的解集,再根据不等式组有解集得出a的取值范围即可.
解:,
由①得,x≥a,
由②得x<1,
∵不等式组有解集,
∴a≤x<1,
∴a<1.
13.分析:利用题中的新定义化简所求不等式,求出a的范围即可.
解:根据题意得:2※x=2x﹣2﹣x+3=x+1,
∵a<x+1<7,即a﹣1<x<6解集中有两个整数解,
∴a的范围为4≤a<5,
故答案为:4≤a<5
14. 分析:先由①-②得3y=6k-6,求出y=2k-2,再把y的值代入②可得到x=k+2,然后利用x与y异号得到或,再解不等式组即可得到k的取值范围.
解:
①-②得3y=6k-6, 解得y=2k-2③, 把③代入②得x-2k+2=-k+4, 解得x=k+2, 所以方程组的解为.2·1·c·n·j·y
∵x与y异号, ∴或, 解第一个不等式组得-2<k<1,解第二个不等式组得无解, 所以k的取值范围是-2<k<1.【来源:21·世纪·教育·网】
三、计算题(本大题共4小题)
15.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分,就是不等式组的解集.
解: ,
解①得:x≥﹣3,
解②得:x<2.
不等式组的解集是:﹣3≤x<2.
16. 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的整数解即可.21·世纪*教育网
解: ,
解①得:x≤3,
解②得:x>﹣1.
则不等式组的解集是:﹣1<x≤3.
则整数解是:0,1,2,3.
17. 分析:先求出每个不等式的解集,再求出不等式组的解集即可.
解:∵解不等式2x+4≥0得:x≥﹣2,
解不等式得:x<1,
∴不等式组的解集是﹣2≤x<1,
∴该不等式组的最大整数解为0.
18. 分析:先把不等式转化为不等式组,然后通过解不等式组来求分式不等式.
解:(1)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:无解,
解②得:﹣2.5<x≤4
所以原不等式的解集是:﹣2.5<x≤4;
(2)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:x>3,
解②得:x<﹣2.
所以原不等式的解集是:x>3或x<﹣2.
一、选择题(本大题共8小题)
1. 等式组的解集在下列数轴上表示正确的是( )
A.
B.
C.
D.
2. 不等式组的解集是( )
A.1<x≤2 B.﹣1<x≤2 C.x>﹣1 D.﹣1<x≤4
3. 已知不等式组的解集中共有5个整数,则a的取值范围为( )
A.7<a≤8 B.6<a≤7 C.7≤a<8 D.7≤a≤8
4. 把不等式组的解集表示在数轴上,正确的是( )
A.B . C. D.
5. 不等式组的所有整数解的和是( )
A.2 B.3 C.5 D.6
6. 对于不等式组下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣<x≤2
7. 小亮在解不等式组时,解法步骤如下:
解不等式①,得x>3,…第一步;
解不等式②,得x>﹣8,…第二步;
所有原不等式组组的解集为﹣8<x<3…第三步.
对于以上解答,你认为下列判断正确的是( )
A.解答有误,错在第一步 B.解答有误,错在第二步
C.解答有误,错在第三步 D.原解答正确无误
8. △ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A.4 B.4或5 C.5或6 D.6
二、填空题(本大题共6小题)
9. 关于x的不等式组的解集是_____.
10. 不等式组的所有整数解是 .
11. 不等式组的所有整数解的积为 .
12. 若不等式组有解,则a的取值范围是 .
13. 对于任意实数m、n,定义一种运运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是 .21教育网
14. 已知关于x、y的方程组的解是一对异号的数,则k的取值范围是_____.
三、计算题(本大题共4小题)
15. 解不等式组并将解集在数轴上表示出来.
16. 求不等式组的解集,并求它的整数解
17. 解不等式组,并写出该不等式组的最大整数解.
18. 阅读材料:解分式不等式<0
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:无解,解②得:﹣2<x<1
所以原不等式的解集是﹣2<x<1
请仿照上述方法解下列分式不等式:
(1)≤0
(2)>0.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:本题应该先对不等式组进行化简,然后在数轴上分别表示出x的取值范围,它们的公共部分就是不等式组的解集.21世纪教育网版权所有
解:不等式可化为:.
在数轴上表示为: 故选B.
2. B
分析:分别解两个不等式得到x>﹣1和x≤2,然后根据大小小大中间找确定不等数组的解集.
解: ,
解①得x>﹣1,
解②得x≤2,
所以不等式组的解集为﹣1<x≤2.
故选B.
3. A
分析:根据不等式组的解集中共有5个整数解,求出a的范围即可.
解:∵不等式组的解集中共有5个整数,
∴a的范围为7<a≤8,故选A.
4. B
分析:先根据不等式组解答得出x的范围再在数轴上进行标记即可。
解:
解不等式(1)得x>-1,
解不等式(2)得x≤1,
所以解集为-1
5.D
分析:先求出不等式组的解集,再求出不等式组的整数解,最后求出答案即可.
解:
∵解不等式①得;x>﹣,
解不等式②得;x≤3,
∴不等式组的解集为﹣<x≤3,
∴不等式组的整数解为0,1,2,3,
0+1+2+3=6,
故选D.
6.B
分析:分别解两个不等式得到x≤4和x>﹣2.5,利用大于小的小于大的取中间可确定不等式组的解集,再写出不等式组的整数解,然后对各选项进行判断.21·cn·jy·com
解::,
解①得x≤4,
解②得x>﹣2.5,
所以不等式组的解集为﹣2.5<x≤4,
所以不等式组的整数解为﹣2,﹣1,0,1,2,3,4.
故选B.
7. A
分析:先计算出每个不等式的解集,再根据过程进行判断。
解:解不等式①,得x>3,
解不等式②,得x>﹣8,
所以原不等式组的解集为x>3.
故选C.
8. B
分析:先设长度为4、12的高分别是a、b边上的,边c上的高为h,△ABC的面积是S,根据三角形面积公式,可求a=,b=,c=,结合三角形三边的不等关系,可得关于h的不等式,解即可.21cnjy.com
解:设长度为4、12的高分别是a,b边上的,边c上的高为h,△ABC的面积是S,那么
a=,b=,c=,
又∵a﹣b<c<a+b,
∴﹣<c<+,
即<<S,
解得3<h<6,
∴h=4或h=5,故选B.
二、填空题(本大题共6小题)
9. 分析:分别求出每个不等式的解集,再求其解集的公共部分即可.
解: 由①得,x≥2, 由②得,x>4, 根据“同大取较大”原则,原不等式组的解集为x>4.
10.分析:先求出两个不等式的解集,再求其公共解,然后写出范围内的整数即可.
解:,
解不等式①得,x>﹣,
解不等式②得,x≤1,
所以不等式组的解集为﹣x≤1,
所以原不等式组的整数解是0,1.
故答案为:0,1.
11.分析:先分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的所有整数解相乘即可求解.www.21-cn-jy.com
解:,
解不等式①得:x,
解不等式②得:x≤50,
∴不等式组的整数解为﹣1,0,1…50,
所以所有整数解的积为0,
故答案为:0.
12.分析:先把x当作已知条件得出不等式的解集,再根据不等式组有解集得出a的取值范围即可.
解:,
由①得,x≥a,
由②得x<1,
∵不等式组有解集,
∴a≤x<1,
∴a<1.
13.分析:利用题中的新定义化简所求不等式,求出a的范围即可.
解:根据题意得:2※x=2x﹣2﹣x+3=x+1,
∵a<x+1<7,即a﹣1<x<6解集中有两个整数解,
∴a的范围为4≤a<5,
故答案为:4≤a<5
14. 分析:先由①-②得3y=6k-6,求出y=2k-2,再把y的值代入②可得到x=k+2,然后利用x与y异号得到或,再解不等式组即可得到k的取值范围.
解:
①-②得3y=6k-6, 解得y=2k-2③, 把③代入②得x-2k+2=-k+4, 解得x=k+2, 所以方程组的解为.2·1·c·n·j·y
∵x与y异号, ∴或, 解第一个不等式组得-2<k<1,解第二个不等式组得无解, 所以k的取值范围是-2<k<1.【来源:21·世纪·教育·网】
三、计算题(本大题共4小题)
15.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分,就是不等式组的解集.
解: ,
解①得:x≥﹣3,
解②得:x<2.
不等式组的解集是:﹣3≤x<2.
16. 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后确定解集中的整数解即可.21·世纪*教育网
解: ,
解①得:x≤3,
解②得:x>﹣1.
则不等式组的解集是:﹣1<x≤3.
则整数解是:0,1,2,3.
17. 分析:先求出每个不等式的解集,再求出不等式组的解集即可.
解:∵解不等式2x+4≥0得:x≥﹣2,
解不等式得:x<1,
∴不等式组的解集是﹣2≤x<1,
∴该不等式组的最大整数解为0.
18. 分析:先把不等式转化为不等式组,然后通过解不等式组来求分式不等式.
解:(1)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:无解,
解②得:﹣2.5<x≤4
所以原不等式的解集是:﹣2.5<x≤4;
(2)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为:
①或②
解①得:x>3,
解②得:x<﹣2.
所以原不等式的解集是:x>3或x<﹣2.
