第3章图形与坐标单元检测B卷

湘教版八年级下第3章图形与坐标单元检测B卷
姓名：__________班级：__________考号：__________
一、单选题（共12题 ）
1、 如图，点A（﹣2，1）到y轴的距离为（　　）
A、-2 B、1 C、2 D、
2、已知A（2，﹣5），AB平行于y轴，则点B的坐标可能是（　　）
A、（﹣2，5） B、（2，6） C、（5，﹣5） D、（﹣5，5）
3、点P在直线y=-x+1上，且到y轴的距离为1，则点P的坐标是（?? ）
A、（1，0） B、（-1，2） C、（1，0）或（-1，2） D、（0，1）
4、将△ABC的三个点坐标的横坐标乘以-1，纵坐标不变，则所得图形与原图的关系是（???）?
A、关于x轴对称 B、关于y轴对称
C、关于原点对称 D、将原图的x轴的负方向平移了了1个单位
5、直线y=﹣2x+m与直线y=2x﹣1的交点在第四象限，则m的取值范围是
A、m＞﹣1 B、m＜1 C、﹣1＜m＜1 D、﹣1≤m≤1
6、如图，在平面直角坐标系中，以点O为圆心，适当长为半径画弧，交x轴于点M ， 交y轴于点N ， 再分别以点M、N为圆心，大于 MN的长为半径画弧，两弧在第二象限交于点P ， 若点P的坐标为（6a ， 2b-1），则a和b的数量关系为（　　）
A、6a-2b=1 B、6a+2b=1 C、6a-b=1 D、6a+b=1
7、如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个 单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2012次相遇地点的坐标是（ ）
A、（2，0） B、（－1，1） C、（－2，1） D、（－1，－1）
8、已知M（a,3）和N（4，b）关于y轴对称，则（a+b）2010的值为（　 　）
A、1　　 B、－1　　　 C、72007 D、-72007
9、已知两点A（3，2）和B（1，－2），点P在y轴上且使AP＋BP最短，则点P的坐标是（　　）．
A、（0， ） B、（0， ） C、（0，－1） D、（0， ）
10、已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标为（　　）
A、（﹣4，0） B、（6，0） C、（﹣4，0）或（6，0） D、无法确定
11、在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0），（5，0），（2，3），则顶点C的坐标是（? ）
A、（3，7） B、（5，3） C、（7，3） D、（8，2）
12、如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作：将线段OP0按逆时针方向旋转60°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转60°，长度伸长为OP1的2倍，得到线段OP2 ， 如此重复操作下去，得到线段OP3 ， OP4 ， …则P32的坐标为（　　）?
A、（﹣231 ， 231） B、（231 ， 231）C、（﹣232 ， 232） D、（232 ， 232）
二、填空题（共6题 ）
13、已知A（－1，－2）和B（1，3），将点A向________平移________个单位长度后得到的点与点B关于y轴对称．
14、点P（m+5，m+1）在直角坐标系的y轴上，则点P的坐标为?________．
15、 如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向左转90°后直行400m到达梅花阁C，则点C的坐标是________?．
16、 菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为________?．
17、如图，在平面直角坐标系中，四边形OABC是正方形，点A的坐标是（4,0），点P为边AB上一点，， 沿CP折叠正方形，折叠后，点B落在平面内点B’处，则点B’的坐标是________?
18、如图：在4×4的网格中存在线段AB，每格表示一个单位长度，并构建了平面直角坐标系．（1）直接写出点A、B的坐标：A（________?，________），B（________?，________）；（2）请在图中确定点C（1，﹣2）的位置并连接AC、BC，则△ABC是________三角形（判断其形状）；（3）在现在的网格中（包括网格的边界）存在一点P，点P的横纵坐标为整数，连接PA、PB后得到△PAB为等腰三角形，则满足条件的点P有________个．
三、解答题（共8题 ）
19、在平面直角坐标系中，点A（a，3﹣2a）在第一象限．（1）若点A到x轴的距离与到y轴的距离相等，求a的值；（2）若点A到x轴的距离小于到y轴的距离，求a的取值范围．

20、若x，y为实数，且满足|x﹣3|+=0．（1）如果实数x，y对应为平面直角坐标系上的点A（x，y），则点A在第几象限？（2）求（）2015的值？
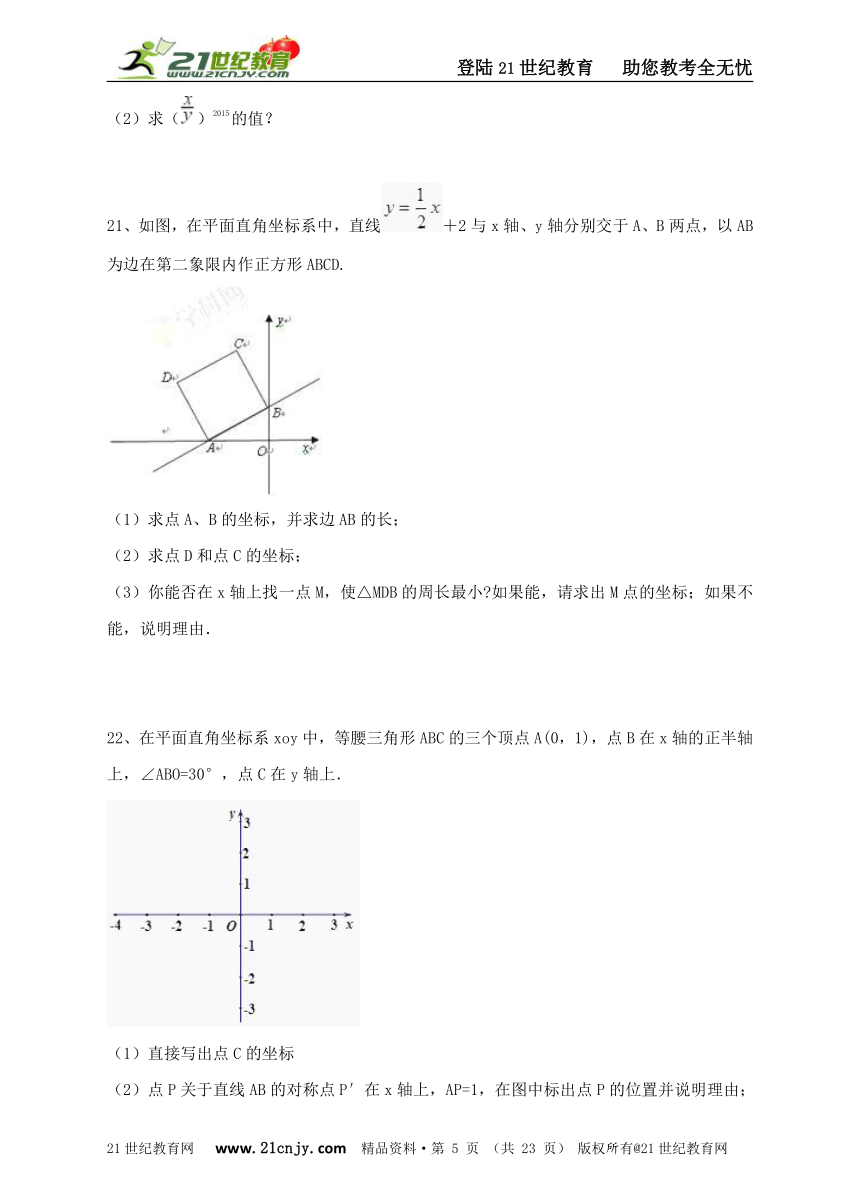
21、如图，在平面直角坐标系中，直线＋2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD. （1）求点A、B的坐标，并求边AB的长；（2）求点D和点C的坐标；（3）你能否在x轴上找一点M，使△MDB的周长最小?如果能，请求出M点的坐标；如果不能，说明理由．
22、在平面直角坐标系xoy中，等腰三角形ABC的三个顶点A(0，1)，点B在x轴的正半轴上，∠ABO=30°，点C在y轴上． （1）直接写出点C的坐标（2）点P关于直线AB的对称点P′在x轴上，AP=1，在图中标出点P的位置并说明理由；（3）在（2）的条件下，在y轴上找到一点M，使PM+BM的值最小，则这个最小值是？

23、位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示．（1）建立适当的平面直角坐标系，使医院的坐标为（3，0）并写出小明家、学校、游乐场的坐标；（2）根据蜀河大坝蓄水工程需要，小明家及学校、医院、游乐场需要等距离整体迁移，已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示，且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，请先在图中描出A、B、C、D的位置，画出四边形ABCD，然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的？
24、在某河流的北岸有A、B两个村子，A村距河北岸的距离为1千米，B村距河北岸的距离为4千米，且两村相距5千米，B在A的右边，现以河北岸为x轴，A村在y轴正半轴上（单位：千米）．（1）请建立平面直角坐标系，并描出A、B两村的位置，写出其坐标．（2）近几年，由于乱砍滥伐，生态环境受到破坏，A、B两村面临缺水的危险．两村商议，共同在河北岸修一个水泵站，分别向两村各铺一条水管，要使所用水管最短，水泵站应修在什么位置在图中标出水泵站的位置，并求出所用水管的长度．
25、如图，一个小正方形网格的边长表示50米．A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校．（1）以学校为坐标原点，向东为x轴正方向，向北为y轴正方向，在图中建立直角坐标系：（2）B同学家的坐标是（3）在你所建的直角坐标系中，如果C同学家的坐标为（﹣150，100），请你在图中描出表示C同学家的点．
26、在平面直角坐标系中，O为坐标原点，点A的坐标为（a，﹣a），点B坐标为（b，c），a，b，c满足． （1）若a没有平方根，判断点A在第几象限并说明理由；（2）若点A到x轴的距离是点B到x轴距离的3倍，求点B的坐标；（3）点D的坐标为（4，﹣2），△OAB的面积是△DAB面积的2倍，求点B的坐标．
答案解析
一、选择题
1。分析：根据点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度解答．
解：点A的坐标为（﹣2，1），则点A到y轴的距离为2．故选C．
2. 分析：根据题意，画出直角坐标系，找出A点，在图上找出经过A点的平行于y轴的直线，那么B点肯定在这条直线上，再根据这条直线的信息确定B点的坐标．
解： ∵直线AB平行于y轴，且A（2，﹣5），∴直线AB上所有点横坐标为2，又∵B点在直线AB上，∴B的横坐标必须是2，A，C，D均不合题意．故选B．
3. 分析：本题考查了一次函数图象上点的坐标特征．解答该题时，要注意：到y轴的距离为1的点P有两个．根据题意知点P的横坐标是x=±1，然后将x的值代入直线方程y=-x+1即可求得点P的纵坐标
解：∵点P在直线y=-x+1上，且到y轴的距离为1，∴点P的横坐标是x=±1；①当x=1时，y=-1+1=0，∴点P的坐标是（1，0)；②当x=-1时，y=-（-1)+1=2，∴点P的坐标是（-1，2)；综合①②，点P的坐标是（1，0)或（-1，2)；故选C．．
4. 分析：熟悉：平面直角坐标系中任意一点P（x，y)，分别关于x轴的对称点的坐标是（x，-y)，关于y轴的对称点的坐标是（-x，y)．
解：根据对称的性质，得三个顶点坐标的横坐标都乘以-1，并保持纵坐标不变，就是横坐标变成相反数．即所得到的点与原来的点关于y轴对称．故选B．
5.解：∵由解得，∴两直线的交点坐标为。∵交点在第四象限，∴根据平面直角坐标系中各象限点的特征，判断其所在象限，四个象限的符号特征分别是：第一象限（＋，＋）；第二象限（－，＋）；第三象限（－，－）；第四象限（＋，－）。因此，。故选C。
6. 分析：根据作图方法可得点P在第二象限的角平分线上，根据角平分线的性质和第二象限内点的坐标符号可得6a+2b-1=0，然后再整理可得答案
解：根据作图方法可得点P在第二象限角平分线上；点P到x轴、y轴的距离相等；点P的横纵坐标互为相反数，则P点横纵坐标的和为0，故6a+2b-1=0（或-6a=2b-1），整理得：6a+2b=1选：B．
7.分析：利用行程问题中的相遇问题，由于矩形的长宽分别为4和2，物体乙是物体甲的速度的2倍，求得每一次相遇的地点，找出规律即可解答．此题主要考查了行程问题中的相遇问题及按比例分配的运用，通过计算发现规律就可以解决问题．
解：矩形的长宽分别为4和2，因为物体乙是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1：2，由题意知：
①第一次相遇物体甲与物体乙行的路程和为12×1，物体甲行的路程为12×=4，物体乙行的路程为12×=8，在BC边相遇；②第二次相遇物体甲与物体乙行的路程和为12×2，物体甲行的路程为12×2×=8，物体乙行的路程为12×2×=16，在DE边相遇；③第三次相遇物体甲与物体乙行的路程和为12×3，物体甲行的路程为12×3×=12，物体乙行的路程为12×3×=24，在A点相遇；…此时甲、乙回到原出发点，则每相遇三次，两点回到出发点，∵2012÷3=670…2，故两个物体运动后的第2012次相遇地点的是：第二次相遇地点，即物体甲行的路程为12×2×=8，物体乙行的路程为12×2×=16，在DE边相遇；此时相遇点的坐标为：（-1，-1)，故选：D．

8.分析：首先根据关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得a=-4，b=3，再计算（a+b)2010的值。【解答】∵点M（a，3)和点N（4，b)关于y轴对称，∴a=-4，b=3，∴（a+b)2010=（-4+3)2010=1，故选A．
9. 分析：根据已知条件和两点间线段最短，可知P点是“其中一点关于y轴的对称点与另一点的连线和y轴的交点
解：根据已知条件，点A关于y轴的对称点A′为（－3，2）．设过A′B的解析式为y＝kx＋b，则－3k＋b＝2；k＋b＝－2．解得k＝－1，b＝－1那么此函数解析式为y＝－x－1．与y轴的交点是（0，－1），此点就是所求的点P．故选C．．
10. 分析：根据B点的坐标可知AP边上的高为2，而△PAB的面积为5，点P在x轴上，说明AP=5，已知点A的坐标，可求P点坐标．
解：∵A（1，0），B（0，2），点P在x轴上，∴AP边上的高为2，又△PAB的面积为5，∴AP=5，而点P可能在点A（1，0）的左边或者右边，∴P（﹣4，0）或（6，0）．故选C．
11. 分析：因为D点坐标为（2，3），由平行四边形的性质，可知C点的纵坐标一定是3，又由D点相对于A点横坐标移动了2，故可得C点横坐标为2+5=7，即顶点C的坐标（7，3）．
解：已知A，B，D三点的坐标分别是（0，0），（5，0），（2，3）， ∵AB在x轴上，∴点C与点D的纵坐标相等，都为3，又∵D点相对于A点横坐标移动了2﹣0=2，∴C点横坐标为2+5=7，∴即顶点C的坐标（7，3）．故选：C．
12. 分析：根据题意得出OP1=2，OP2=4，OP3=8，进而得出P点坐标变化规律，得出点P23的坐标即可．
解：由题意可得出：OP1=2，OP2=4=22 ， OP3=8=23 ， 则OP32=232 ， ∵将线段OP按逆时针方向旋60°，∴每6个点循环一圈，∵32÷6=5…2，∴点P32的坐标与点P2的坐标在第2象限，∵OP32=232 ， ∴P32到x轴的距离为：232?sin60°=231?到y轴的距离为232?cos60°=231 ， ∴点P32的坐标是：（﹣231?，231?）．故选：A．
二、填空题
13. 分析：关于y轴对称的两点的坐标特点为横坐标互为相反数，纵坐标相等．
解：点B关于y轴对称点的坐标为（－1，3），由点A（－1，－2）得到点（－1，3）需向上平移5个单位长度．
14. 分析：根据y轴上点的横坐标等于零，可得关于m的方程，根据m的值，可得答案．
解：由P（m+5，m+1）在直角坐标系的y轴上，得m+5=0，解得m=﹣5．m+1=﹣4，点P的坐标为（0，﹣4），故答案为：（0，﹣4）．
15. 分析：根据题意结合全等三角形的判定与性质得出△AOD≌△ACB（SAS），进而得出C，A，D也在一条直线上，求出CD的长即可得出C点坐标．
解：连接AC，由题意可得：AB=300m，BC=400m，在△AOD和△ACB中∵，∴△AOD≌△ACB（SAS），∴∠CAB=∠OAD，∵B、O在一条直线上，∴C，A，D也在一条直线上，∴AC=AO=500m，则CD=AC=AD=800m，∴C点坐标为：（400，800）．故答案为：（400，800）．
16. 分析：点B的对称点是点D，连接ED，交OC于点P，再得出ED即为EP+BP最短，解答即可．
解：连接ED，如图， ∵点B的对称点是点D，∴DP=BP，∴ED即为EP+BP最短，∵四边形ABCD是菱形，顶点B（2，0），∠DOB=60°，∴点D的坐标为（1，），∴点C的坐标为（3，），∴可得直线OC的解析式为：y=x，∵点E的坐标为（0，﹣1），∴可得直线ED的解析式为：y=（1+）x﹣1， ∵点P是直线OC和直线ED的交点，∴点P的坐标为方程组的解，解方程组得：，所以点P的坐标为（2-32-），故答案为：（2-32-）．
17. 分析：此题考查了图形的翻折变换性质。
解：过点B′作B′D⊥y轴于D，B′E⊥x轴于E， ∵OABC是正方形，点A的坐标是（4，0），点C的坐标是（0，4），∴BC=OC=4，∵∠BPC=60°，∴由折叠的性质求得B′C=BC=4，∠B′CP=∠BCP=30°∴∠DCB′=90°﹣∠B′CP﹣∠BCP=30°，∴B′D=B′C=CB=2，CD=BC=，∴OD=OC﹣CD=4﹣2， ∴B’点的坐标为．
18. 分析：（1）根据平面直角坐标系可直接写出A、B的坐标；（2）画出图形，利用勾股定理计算出AB2、CB2、AC2 ， 再利用逆定理证明△ACB是等腰直角三角形；（3）分别以A、B为圆心，AB长为半径画圆可得P的位置及个数．
解：（1）根据平面直角坐标系可得A（0，1），B（﹣1，﹣1），故答案为：0；1；﹣1；﹣1；（2）∵AB2=12+22=5，CB2=12+22=5，AC2=12+32=10，∴AB2+BC2=AC2 ， ∴△ACB是等腰直角三角形，故答案为：等腰直角；（3）如图所示：， 满足条件的点P有8个，故答案为：8．
三、解答题
19. 分析：（1）根据第一象限内点的横坐标与纵坐标都是正数，到x、y轴的距离相等列出方程求解即可；（2）根据点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度列出不等式，然后求解即可．
解：（1）∵点A（a，3﹣2a）在第一象限∴点A到y轴的距离为a、到x轴的距离为3﹣2a，∴a=3﹣2a，解得a=1；（2）∵点A到x轴的距离小于到y轴的距离，∴a＞3﹣2a，解得a＞1，∵点A（a，3﹣2a）在第一象限，∴，即0＜a＜，∴当1＜a＜?时，点A到x轴的距离小于到y轴的距离．
20. 分析：（1）由绝对值、偶次方根的非负性，可以求出x、y的值，写出点的坐标即可以求出点A的象限；（2）由（1）中求得x、y值，得?=﹣1，进而求出答案．
解：（1）∵|x+3|≥0，≥0，且|x﹣3|+=0，∴x﹣3=0，y+3=0，∴x=3，y=﹣3，∴A（3，﹣3），∴点A在第四象限．（2）由（1）得：x=3，y=﹣3，∴=﹣1，∴（）2015=﹣1．
21. 分析：（1）要求A,B点的坐标，实际上就是求一次函数与两坐标轴的交点问题，那么就令x=0及y=0可以求出A,B点的坐标，由此就可以求出AB的长度（2）要求点C,D的坐标首先需要证△DEA≌△AOB，证出OA=DE，AE=OB，即可求出D的坐标，同理可以求出点C的坐标；（3）先作出D关于X轴的对称点F，连接BF，BF于X轴交点M就是符合条件的点，求出F的坐标，进而求出直线BF，再求出与X轴交点即可．
解：（1）当y=0时，x=－4，则A的坐标（－4，0），当x=0时，y="2" ，则B的坐标（0，2），∴;（2）过D做线段DE垂直x轴，交x轴与E则△DEA≌△AOB ，∴DE=AO＝4，EA＝OB＝2∴D的坐标为（－6，4），同理可得C的坐标为（－2，6）; (3)作B关于x轴的对称点， 连接M,与x轴的交点即为点M,则（0，-2），设直线M的解析式为， 则有直线M的解析式为当y=0，x=-2，则M的坐标为（-2,0）. ?
22. 分析：（1）先确定A的位置，再作出△AOB，就可以求出AB=2，OB=， 在y轴上符合条件的有两点C1和C2，求出即可；（2）根据AP=AO=1，得出P的对称点是O点，求出OC，即可得出OP，解直角三角形求出PQ和OQ即可；（3）作出B关于y轴的对称点，连接PB′即可得出M点的位置，求出PB′长即可．
解：（1）符合条件的有两点，以A为圆心，以AB为半径画弧，交y轴于C1、C2点， ∵A（0，1），∴OA=1，∵在Rt△AOB中，OA=1，∠ABO=30°，∴AB=2OA=2，OB=， 即AC1=AC2=2，∴OC1=1+2=3，OC2=2-1=2，∴C的坐标是（0，3）或（0，-1），（2）P的坐标是（， ?），理由是：过P作PQ⊥x轴于Q，∵OA=1，AP=1，AO⊥x轴，∴x轴和以A为圆心，以1为半径的圆相切，∵AP=1，∴P在圆上，∵点P关于直线AB的对称点P′在x轴上，AP=1，∴P′点和O重合，如图： ∵P和P′关于直线AB对称，∴PP′⊥AB，PC=P′C，由三角形面积公式得：S△AOB=AO×OB=AB×CO，∴×1=2OC，∴OC=， ∴PP′=2OC=， ∵∠ABO=30°，∠OCB=90°，∴∠POB=60°，∴PQ=OP×sin60°=?，OQ=OP×cos60°=， 即P的坐标是（， ）；（3）作B关于y轴的对称点B′，连接PB′交y轴于M，则M为所求， ∵OB=， ∴OB′=， 即BB′=2， ∵PQ=， ∴由勾股定理得：PB′=， ∴PM+BM=PM+B′M=PB′=．
23. 分析：（1）首先建立平面直角坐标系，进而得出小明家、学校、游乐场的坐标；（2）利用平移规律得出各对应点位置，进而得出答案．
解：（1）如图所示：小明家的坐标为：（0，0）、学校的坐标为：（2，2）、游乐场的坐标为：（5，2）；（2）∵四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，∴A、B、C、D的位置如图所示，则四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过向左平移5个单位再向上平移2个单位得到的．?
24.分析：（1）根据题意建立坐标系解答；（2）利用两点之间线段最短的数学道理作图即可．
解：（1）如图，点A（0，1），点B（4，4）； （2）找A关于x轴的对称点A′，连接A′B交x轴于点P，则P点即为水泵站的位置，PA+PB=PA′+PB=A′B且最短（如图）．过B、A′分别作x轴、y轴的垂线交于E，作AD⊥BE，垂足为D，则BD=3，在Rt△ABD中，AD==4，所以A点坐标为（0，1），B点坐标为（4，4），A′点坐标为（0，﹣1），由A′E=4，BE=5，在Rt△A′BE中，A′B==．故所用水管最短长度为千米．
25. 分析：（1）由于A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校，则可确定A点位置，然后画出直角坐标系；（2）利用第一象限点的坐标特征写出B点坐标；（3）根据坐标的意义描出点C．
解：（1）如图，（2）B同学家的坐标是（200，150）；（3）如图．故答案为（200，150）．
26. 分析：（1）根据平方根的意义得到a＜0，然后根据各象限点的坐标特征可判断点A在第二象限；（2）先利用方程组， 用a表示b、c得b=a，c=4﹣a，则B点坐标为（a，4﹣a），再利用点A到x轴的距离是点B到x轴距离的3倍得到|﹣a|=3|4﹣a|，则a=3（4﹣a）或a=﹣3（4﹣a），分别解方程求出a的值，然后计算出c的值，于是可写出B点坐标；（3）利用A（a，﹣a）和B（a，4﹣a）得到AB=4，AB与y轴平行，由于点D的坐标为（4，﹣2），△OAB的面积是△DAB面积的2倍，则判断点A、点B在y轴的右侧，即a＞0，根据三角形面积公式得到×4×a=2××4×|4﹣a|，解方程得a=或a=8，然后写出B点坐标．
解：（1）∵a没有平方根，∴a＜0，∴﹣a＞0，∴点A在第二象限；（2）解方程组，用a表示b、c得b=a，c=4﹣a，∴B点坐标为（a，4﹣a），∵点A到x轴的距离是点B到x轴距离的3倍，∴|﹣a|=3|4﹣a|，当a=3（4﹣a），解得a=3，则c=4﹣3=1，此时B点坐标为（3，1）；当a=﹣3（4﹣a），解得a=6，则c=4﹣6=﹣2，此时B点坐标为（6，﹣2）；综上所述，B点坐标为（3，1）或（6，﹣2）；（3）∵点A的坐标为（a，﹣a），点B坐标为（a，4﹣a），∴AB=4，AB与y轴平行，∵点D的坐标为（4，﹣2），△OAB的面积是△DAB面积的2倍，∴点A、点B在y轴的右侧，即a＞0，∴×4×a=2××4×|4﹣a|，解得a=或a=8，∴B点坐标为（，）或（8，﹣4）．