湖北省宜昌市部分重点中学2016-2017学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 湖北省宜昌市部分重点中学2016-2017学年高二(上)期末数学试卷(文科)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 315.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 00:00:00 | ||
图片预览




文档简介
2016-2017学年湖北省宜昌市部分重点中学高二(上)期末数学试卷(文科)
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数的共轭复数是( )
A.i+2
B.i﹣2
C.﹣2﹣i
D.2﹣i
2.命题:“ x0∈R,”的否定为( )
A. x∈R,
B. x∈R,
C. x∈R,
D. x∈R,
3.在长为3m的线段AB上任取一点P,则点P与线段两端点A、B的距离都大于1m的概率是( )
A.
B.
C.
D.
4.经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
A.y=2x或x﹣y+1=0
B.y=2x,x+y﹣3=0
C.x+y﹣3=0,或x﹣y+1=0
D.y=2x,或x+y﹣3=0,或x﹣y+1=0
5.某产品的广告费用x与销售额y的不完整统计数据如表:
广告费用x(万元)
3
4
5
销售额y(万元)
22
28
m
若已知回归直线方程为=9x﹣6,则表中m的值为( )
A.40
B.39
C.38
D.37
6.已知约束条件若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
A.0<a<
B.a≥
C.a>
D.0<a<
7.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )
A.24
B.20
C.0
D.﹣4
8.如图,给出的是计算×××…×的值的程序框图,其中判断框内不能填入的是( )
A.i≤2017?
B.i<2018?
C.i≤2015?
D.i≤2016?
9.“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
10.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
11.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是( )
A.若m、n都平行于平面α,则m、n一定不是相交直线
B.若m、n都垂直于平面α,则m、n一定是平行直线
C.已知α、β互相平行,m、n互相平行,若m∥α,则n∥β
D.若m、n在平面α内的射影互相平行,则m、n互相平行
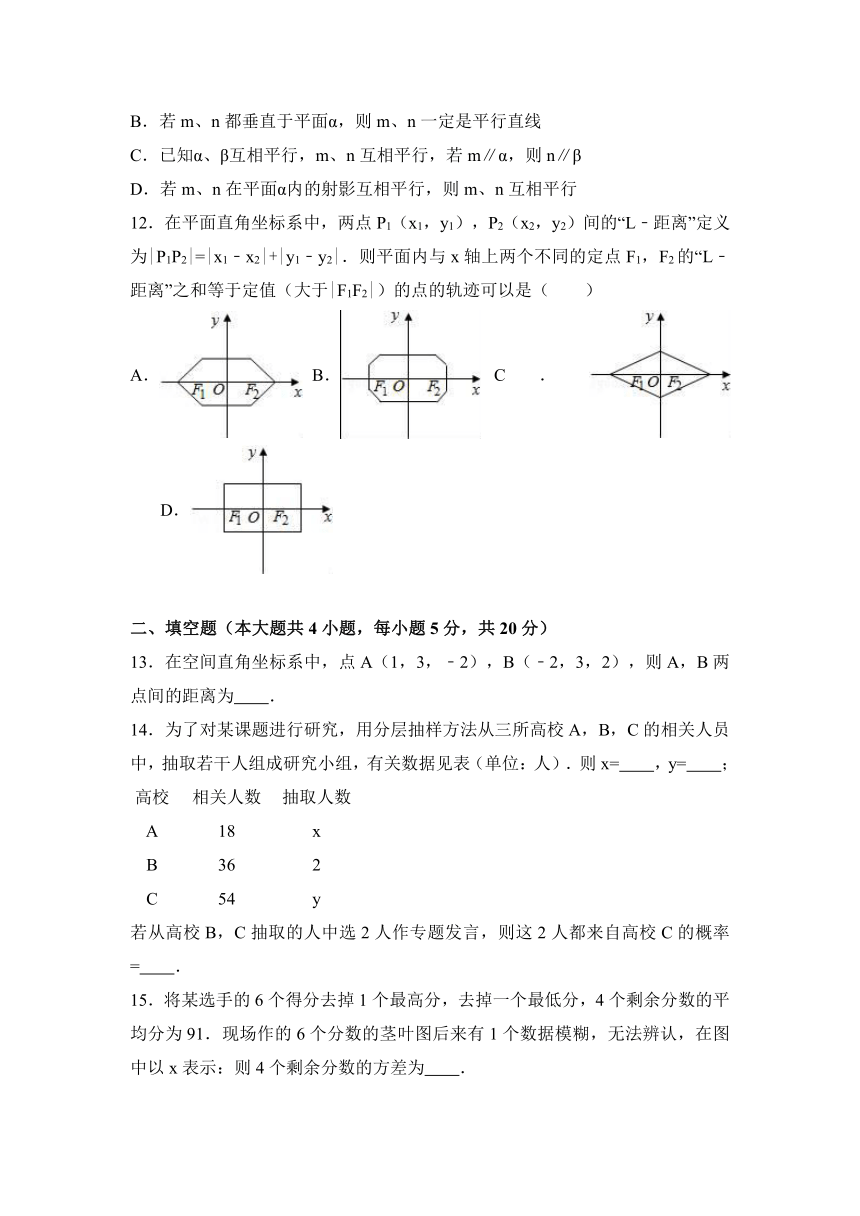
12.在平面直角坐标系中,两点P1(x1
( http: / / www.21cnjy.com ),y1),P2(x2,y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.则平面内与x轴上两个不同的定点F1,F2的“L﹣距离”之和等于定值(大于|F1F2|)的点的轨迹可以是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),则A,B两点间的距离为 .
14.为了对某课题进行研究,用分层抽样方法
( http: / / www.21cnjy.com )从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人).则x= ,y= ;
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
若从高校B,C抽取的人中选2人作专题发言,则这2人都来自高校C的概率= .
15.将某选手的6个得分去掉1个最高分,去
( http: / / www.21cnjy.com )掉一个最低分,4个剩余分数的平均分为91.现场作的6个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:则4个剩余分数的方差为 .
16.已知双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),则a= ,b= .
三、解答题(17小题10分,18-22小题每题12分;共70分)
17.我国是世界上严重缺水
( http: / / www.21cnjy.com )的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
18.已知命题p: x∈R,不等式恒成立,命题q:椭圆的焦点在x轴上.若命题p∨q为真命题,求实数m的取值范围.
19.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
20.如图,四棱锥P﹣ABCD中,PA
( http: / / www.21cnjy.com )⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
21.袋子中放有大小和形状相同的小
( http: / / www.21cnjy.com )球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(I)求n的值;
(II)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.
22.已知椭圆+=1(a>b>
( http: / / www.21cnjy.com )0)的左右焦点分别为F1和F2,由4个点M(﹣a,b)、N(a,b)、F2和F1组成了一个高为,面积为3的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A、B,求△F2AB面积的最大值.
2016-2017学年湖北省宜昌市部分重点中学高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数的共轭复数是( )
A.i+2
B.i﹣2
C.﹣2﹣i
D.2﹣i
【考点】复数的基本概念;复数代数形式的乘除运算.
【分析】首先要对所给的复数进行整理,分子和分母同乘以分母的共轭复数,化简到最简形式,把得到的复数虚部变为相反数,得到要求的共轭复数.
【解答】解:∵复数==﹣2﹣i,
∴共轭复数是﹣2+i
故选B.
2.命题:“ x0∈R,”的否定为( )
A. x∈R,
B. x∈R,
C. x∈R,
D. x∈R,
【考点】命题的否定.
【分析】根据已知中的原命题,结合特称命题否定的定义,可得答案.
【解答】解:命题:“ x0∈R,”的否定为“ x∈R,”,
故选:B
3.在长为3m的线段AB上任取一点P,则点P与线段两端点A、B的距离都大于1m的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】由题意可得,属于与区间长度有关的几何概率模型,试验的全部区域长度为3,基本事件的区域长度为1,代入几何概率公式可求
【解答】解:设“长为3m的线段AB”对应区间[0,3]
“与线段两端点A、B的距离都大于1m”为事件
A,则满足A的区间为[1,2]
根据几何概率的计算公式可得,
故选:B
4.经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
A.y=2x或x﹣y+1=0
B.y=2x,x+y﹣3=0
C.x+y﹣3=0,或x﹣y+1=0
D.y=2x,或x+y﹣3=0,或x﹣y+1=0
【考点】待定系数法求直线方程.
【分析】直线在两个坐标轴上的截距的绝对值相等,有三种情况,一是过原点,二是斜率为1,三是斜率为﹣1,分别求解即可.
【解答】解:经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线:
当截距为0时,直线过原点:y=2x;
当斜率为1时,直线方程:x﹣y+1=0;
当斜率为﹣1时,直线方程:x+y﹣3=0.
综上所述,直线方程为y=2x或x+y﹣3=0或x﹣y+1=0.
故选D.
5.某产品的广告费用x与销售额y的不完整统计数据如表:
广告费用x(万元)
3
4
5
销售额y(万元)
22
28
m
若已知回归直线方程为=9x﹣6,则表中m的值为( )
A.40
B.39
C.38
D.37
【考点】线性回归方程.
【分析】求出数据中心(,),代入回归方程解出m.
【解答】解:由题意,回归方程过样本平均数点(,),可求出=4
代入得;
=36﹣6=30,
则30=,∴m=40.
故选:A.
6.已知约束条件若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
A.0<a<
B.a≥
C.a>
D.0<a<
【考点】简单线性规划的应用.
【分析】先根据约束条件画出可行域,再利用几何意义求最值的方法,利用直线斜率之间的关系,只需求出直线z=x+ay的斜率的取值范围即可.
【解答】解:画出已知约束条件的可行域为△ABC内部(包括边界),
如图,易知当a=0时,不符合题意;
当a>0时,由目标函数z=x+ay得y=﹣x+,
则由题意得﹣3=kAC<﹣<0,故a>.
综上所述,a>.
故选C.
7.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )
A.24
B.20
C.0
D.﹣4
【考点】直线的一般式方程与直线的垂直关系.
【分析】先由两直线平行斜率相等,求出m,第一直线的方程确定了,把垂足坐标代入,可求p,垂足坐标确定了.
把垂足坐标代入第二条直线的方程可得
n,进而求得m﹣n+p的值.
【解答】解:∵直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,
∴×=﹣1,
∴m=10,
直线mx+4y﹣2=0
即
5x+2y﹣1=0,垂足(1,p)代入得,5+2p﹣1=0,∴p=﹣2.
把P(1,﹣2)代入2x﹣5y+n=0,可得
n=﹣12,
∴m﹣n+p=20,
故选B.
8.如图,给出的是计算×××…×的值的程序框图,其中判断框内不能填入的是( )
A.i≤2017?
B.i<2018?
C.i≤2015?
D.i≤2016?
【考点】程序框图.
【分析】根据程序运行后输出的算式,分析倒数第一圈,即i=2016时满足条件,i=2018不满足循环条件;由此可得判断框内不能填入的选项.
【解答】解:∵程序运行后输出的是S=×××…×的值,
∴分析倒数第一圈,i=2016时,满足条件,执行循环S=×××…×,
i=i+2=2018,此时不满足条件,终止循环,输出S=×××…×的值;
∴判断框内能填入“i≤2017?”,“i<2018?”,“i≤2016?”,
不能填入“i≤2015?”.
故选:C.
9.“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】直线的一般式方程与直线的平行关系.
【分析】根据充分必要条件的定义,分别进行判断从而得到结论.
【解答】解:m=1时,直线mx+y﹣2=0与直线x+my+1﹣m=0相互平行,是充分条件,
若直线mx+y+2=0与直线x+my+1﹣m=0相互平行,
则,解得:m=1,是必要条件,
故选:C.
10.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
【考点】由三视图求面积、体积.
【分析】三视图复原的几何体是一个半圆锥和圆柱的组合体,根据三视图的数据,求出半圆锥和圆柱的体积,相加可得答案.
【解答】解:三视图复原的几何体是一个半圆锥和圆柱的组合体,
它们的底面直径均为2,故底面半径为1,
圆柱的高为1,半圆锥的高为2,
故圆柱的体积为:π×12×1=π,
半圆锥的体积为:×=,
故该几何体的体积V=π+=,
故选:B
11.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是( )
A.若m、n都平行于平面α,则m、n一定不是相交直线
B.若m、n都垂直于平面α,则m、n一定是平行直线
C.已知α、β互相平行,m、n互相平行,若m∥α,则n∥β
D.若m、n在平面α内的射影互相平行,则m、n互相平行
【考点】命题的真假判断与应用;空间中直线与直线之间的位置关系;空间中直线与平面之间的位置关系;平面与平面之间的位置关系.
【分析】A,平行于同一平面的两条直线可能相交,也可能平行;
B,垂直于同一平面的两条直线一定平行;
C,α、β互相平行,m、n互相平行,若m∥α,则n∥β或
n β;
D,m、n在平面α内的射影互相平行,则m、n互相平行或相交,
【解答】解:对于A,平行于同一平面的两条直线可能相交,也可能平行,故错;
对于B,垂直于同一平面的两条直线一定平行,故正确;
对于C,α、β互相平行,m、n互相平行,若m∥α,则n∥β或
n β,故错;
对于D,m、n在平面α内的射影互相平行,则m、n互相平行或相交,故错,
故选:B.
12.在平面直角坐标系中,两点P1(x1,y
( http: / / www.21cnjy.com )1),P2(x2,y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.则平面内与x轴上两个不同的定点F1,F2的“L﹣距离”之和等于定值(大于|F1F2|)的点的轨迹可以是( )
A.
B.
C.
D.
【考点】轨迹方程.
【分析】设出F1,F2的坐标,在设出动点M的坐标,由新定义列式后分类讨论去绝对值,然后结合选项得答案.
【解答】解:设F1(﹣c,0),F2(c,0),
再设动点M(x,y),动点到定点F1,F2的“L﹣距离”之和等于m(m>2c>0),
由题意可得:|x+c|+|y|+|x﹣c|+|y|=m,
即|x+c|+|x﹣c|+2|y|=m.
当x<﹣c,y≥0时,方程化为2x﹣2y+m=0;
当x<﹣c,y<0时,方程化为2x+2y+m=0;
当﹣c≤x<c,y≥0时,方程化为y=;
当﹣c≤x<c,y<0时,方程化为y=c﹣;
当x≥c,y≥0时,方程化为2x+2y﹣m=0;
当x≥c,y<0时,方程化为2x﹣2y﹣m=0.
结合题目中给出的四个选项可知,选项A中的图象符合要求.
故选:A.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),则A,B两点间的距离为 5 .
【考点】空间两点间的距离公式.
【分析】利用空间中两点间的距离公式求解.
【解答】解:∵在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),
∴A,B两点间的距离:
|AB|==5,
故答案为:5.
14.为了对某课题进行研究
( http: / / www.21cnjy.com ),用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人).则x= 1 ,y= 3 ;
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
若从高校B,C抽取的人中选2人作专题发言,则这2人都来自高校C的概率= .
【考点】频率分布表.
【分析】由已知得,由此能求出x=1,y=3,从高校B,C抽取的人中选2人作专题发言,基本事件总数n==10,这2人都来自高校C包含基本事件个数m==3,由此能求出这2人都来自高校C的概率.
【解答】解:由已知得,
解得x=1,y=3,
从高校B,C抽取的人中选2人作专题发言,
基本事件总数n==10,
这2人都来自高校C包含基本事件个数m==3,
∴这2人都来自高校C的概率:p=.
故答案为:1,3,.
15.将某选手的6个得分去掉1个最高分
( http: / / www.21cnjy.com ),去掉一个最低分,4个剩余分数的平均分为91.现场作的6个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:则4个剩余分数的方差为 .
【考点】茎叶图.
【分析】根据茎叶图求出平均数,即可计算方差的大小.
【解答】解:去掉最低分87,若x≥3,则90+x被去掉,
此时剩余的分数为90,90,91,93,平均数为91,
满足条件,
此时对应的方差为
[(90﹣91)2+(90﹣91)2+(91﹣91)2+(93﹣91)2]=(1+1+4)=,
故答案为:.
16.已知双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),则a= 1 ,b= 2 .
【考点】双曲线的标准方程.
【分析】由双曲的一条渐近线为2x+y=0,一个焦点为(,0),列出方程组,由此能出a,b.
【解答】解:∵双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),
∴,
解得a=1,b=2.
故答案为:1,2.
三、解答题(17小题10分,18-22小题每题12分;共70分)
17.我国是世界上严重缺水的国家,某市
( http: / / www.21cnjy.com )为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
【考点】频率分布直方图;众数、中位数、平均数.
【分析】(I)先根据频率分布直方图中的频率等于纵坐标乘以组距求出9个矩形的面积即频率,再根据直方图的总频率为1求出a的值;
(II)根据已知中的频率分布直方图先求出月均用水量不低于3吨的频率,结合样本容量为30万,进而得解.
(Ⅲ)根据频率分布直方图,求出使直方图中左右两边频率相等对应的横坐标的值.
【解答】解:(I)∵1=(0.08
( http: / / www.21cnjy.com )+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5,整理可得:2=1.4+2a,
∴解得:a=0.3.
(II)估计全市居民中月均用水量不低于3吨的人数为3.6万,理由如下:
由已知中的频率分布直方图可得月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12,
又样本容量=30万,
则样本中月均用水量不低于3吨的户数为30×0.12=3.6万.
(Ⅲ)根据频率分布直方图,得;
0.08×0.5+0.16×0.5+0.30×0.5+0.40×0.5=0.47<0.5,
0.47+0.5×0.52=0.73>0.5,
∴中位数应在(2,2.5]组内,设出未知数x,
令0.08×0.5+0.16×0.5+0.30×0.5+0.4×0.5+0.5×x=0.5,
解得x=0.06;
∴中位数是2+0.06=2.06.
18.已知命题p: x∈R,不等式恒成立,命题q:椭圆的焦点在x轴上.若命题p∨q为真命题,求实数m的取值范围.
【考点】复合命题的真假.
【分析】分别求出p,q为真时的m的范围,根据p∨q为假命题,得到关于m的不等式组,解出即可.
【解答】解:p真:,∴…
q真:m﹣1>3﹣m>0∴2<m<3…6分
若p∨q为假命题,则…
∴实数m的取值范围是…
19.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
【考点】解三角形.
【分析】(Ⅰ)已知等式利用正弦定理化简,
( http: / / www.21cnjy.com )整理后利用两角和与差的正弦函数公式及诱导公式化简,根据sinC不为0求出cosC的值,即可确定出出C的度数;
(2)利用余弦定理列出关系式,利用三角形面积公式列出关系式,求出a+b的值,即可求△ABC的周长.
【解答】解:(Ⅰ)已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
∵sinC≠0,sin(A+B)=sinC
∴cosC=,
又0<C<π,
∴C=;
(Ⅱ)由余弦定理得7=a2+b2﹣2ab ,
∴(a+b)2﹣3ab=7,
∵S=absinC=ab=,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周长为5+.
20.如图,四棱锥P﹣ABCD中,P
( http: / / www.21cnjy.com )A⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.
【分析】(Ⅰ)取BC中点E,连结EN,EM,得NE是△PBC的中位线,推导出四边形ABEM是平行四边形,由此能证明MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,NF是△
( http: / / www.21cnjy.com )PAC的中位线,推导出NF⊥面ABCD,延长BC至G,使得CG=AM,连结GM,则四边形AGCM是平行四边形,由此能求出四面体N﹣BCM的体积.
【解答】证明:(Ⅰ)取BC中点E,连结EN,EM,
∵N为PC的中点,∴NE是△PBC的中位线
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN 平面NEM,∴MN∥平面PAB.
解:(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF==2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AMCG,∴四边形AGCM是平行四边形,
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=,
∴S△BCM===2,
∴四面体N﹣BCM的体积VN﹣BCM===.
21.袋子中放有大小和形状相同
( http: / / www.21cnjy.com )的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(I)求n的值;
(II)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.
【考点】几何概型;古典概型及其概率计算公式.
【分析】(Ⅰ)利用从袋子中随机抽取1个小球,取到标号是2的小球的概率是,确定n的值.
(Ⅱ)①从袋子中不放回地随机抽取2个球
( http: / / www.21cnjy.com ),共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率.②记“x2+y2>(a﹣b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型可求得结论.
【解答】解:(Ⅰ)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是可得,
解得n=2.
(Ⅱ)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,则P(A)=.
②记“x2+y2>(a﹣b)2恒成立”为事
( http: / / www.21cnjy.com )件B,则事件B等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},
所以P(B)=1﹣.
22.已知椭圆+=1(a>b>0)的左右焦点分别为F1和F2,由4个点M(﹣a,b)、N(a,b)、F2和F1组成了一个高为,面积为3的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A、B,求△F2AB面积的最大值.
【考点】直线与圆锥曲线的关系;椭圆的标准方程.
【分析】解:(1)由题意知b=,
=3,即a+c=3①,又a2=3+c2②,联立①②解得a,c,;
(2)设A(x1,y1),B(x2,y
( http: / / www.21cnjy.com )2),过点F1的直线方程为x=ky﹣1,代入椭圆方程消掉x得y的二次方程,△F2AB的面积S==|y1﹣y2|=,由韦达定理代入面积表达式变为k的函数,适当变形借助函数单调性即可求得S的最大值;
【解答】解:(1)由题意知b=,
=3,所以a+c=3①,
又a2=b2+c2,即a2=3+c2②,
联立①②解得a=2,c=1,
所以椭圆方程为:;
(2)由(1)知F1(﹣1,0),
设A(x1,y1),B(x2,y2),过点F1的直线方程为x=ky﹣1,
由得(3k2+4)y2﹣6ky﹣9=0,△>0成立,
且,,
△F2AB的面积S==|y1﹣y2|=
==12=,
又k2≥0,所以递增,
所以9+1+6=16,
所以≤=3,当且仅当k=0时取得等号,
所以△F2AB面积的最大值为3.
2017年3月7日
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数的共轭复数是( )
A.i+2
B.i﹣2
C.﹣2﹣i
D.2﹣i
2.命题:“ x0∈R,”的否定为( )
A. x∈R,
B. x∈R,
C. x∈R,
D. x∈R,
3.在长为3m的线段AB上任取一点P,则点P与线段两端点A、B的距离都大于1m的概率是( )
A.
B.
C.
D.
4.经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
A.y=2x或x﹣y+1=0
B.y=2x,x+y﹣3=0
C.x+y﹣3=0,或x﹣y+1=0
D.y=2x,或x+y﹣3=0,或x﹣y+1=0
5.某产品的广告费用x与销售额y的不完整统计数据如表:
广告费用x(万元)
3
4
5
销售额y(万元)
22
28
m
若已知回归直线方程为=9x﹣6,则表中m的值为( )
A.40
B.39
C.38
D.37
6.已知约束条件若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
A.0<a<
B.a≥
C.a>
D.0<a<
7.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )
A.24
B.20
C.0
D.﹣4
8.如图,给出的是计算×××…×的值的程序框图,其中判断框内不能填入的是( )
A.i≤2017?
B.i<2018?
C.i≤2015?
D.i≤2016?
9.“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
10.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
11.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是( )
A.若m、n都平行于平面α,则m、n一定不是相交直线
B.若m、n都垂直于平面α,则m、n一定是平行直线
C.已知α、β互相平行,m、n互相平行,若m∥α,则n∥β
D.若m、n在平面α内的射影互相平行,则m、n互相平行
12.在平面直角坐标系中,两点P1(x1
( http: / / www.21cnjy.com ),y1),P2(x2,y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.则平面内与x轴上两个不同的定点F1,F2的“L﹣距离”之和等于定值(大于|F1F2|)的点的轨迹可以是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),则A,B两点间的距离为 .
14.为了对某课题进行研究,用分层抽样方法
( http: / / www.21cnjy.com )从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人).则x= ,y= ;
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
若从高校B,C抽取的人中选2人作专题发言,则这2人都来自高校C的概率= .
15.将某选手的6个得分去掉1个最高分,去
( http: / / www.21cnjy.com )掉一个最低分,4个剩余分数的平均分为91.现场作的6个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:则4个剩余分数的方差为 .
16.已知双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),则a= ,b= .
三、解答题(17小题10分,18-22小题每题12分;共70分)
17.我国是世界上严重缺水
( http: / / www.21cnjy.com )的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
18.已知命题p: x∈R,不等式恒成立,命题q:椭圆的焦点在x轴上.若命题p∨q为真命题,求实数m的取值范围.
19.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
20.如图,四棱锥P﹣ABCD中,PA
( http: / / www.21cnjy.com )⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
21.袋子中放有大小和形状相同的小
( http: / / www.21cnjy.com )球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(I)求n的值;
(II)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.
22.已知椭圆+=1(a>b>
( http: / / www.21cnjy.com )0)的左右焦点分别为F1和F2,由4个点M(﹣a,b)、N(a,b)、F2和F1组成了一个高为,面积为3的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A、B,求△F2AB面积的最大值.
2016-2017学年湖北省宜昌市部分重点中学高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数的共轭复数是( )
A.i+2
B.i﹣2
C.﹣2﹣i
D.2﹣i
【考点】复数的基本概念;复数代数形式的乘除运算.
【分析】首先要对所给的复数进行整理,分子和分母同乘以分母的共轭复数,化简到最简形式,把得到的复数虚部变为相反数,得到要求的共轭复数.
【解答】解:∵复数==﹣2﹣i,
∴共轭复数是﹣2+i
故选B.
2.命题:“ x0∈R,”的否定为( )
A. x∈R,
B. x∈R,
C. x∈R,
D. x∈R,
【考点】命题的否定.
【分析】根据已知中的原命题,结合特称命题否定的定义,可得答案.
【解答】解:命题:“ x0∈R,”的否定为“ x∈R,”,
故选:B
3.在长为3m的线段AB上任取一点P,则点P与线段两端点A、B的距离都大于1m的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】由题意可得,属于与区间长度有关的几何概率模型,试验的全部区域长度为3,基本事件的区域长度为1,代入几何概率公式可求
【解答】解:设“长为3m的线段AB”对应区间[0,3]
“与线段两端点A、B的距离都大于1m”为事件
A,则满足A的区间为[1,2]
根据几何概率的计算公式可得,
故选:B
4.经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
A.y=2x或x﹣y+1=0
B.y=2x,x+y﹣3=0
C.x+y﹣3=0,或x﹣y+1=0
D.y=2x,或x+y﹣3=0,或x﹣y+1=0
【考点】待定系数法求直线方程.
【分析】直线在两个坐标轴上的截距的绝对值相等,有三种情况,一是过原点,二是斜率为1,三是斜率为﹣1,分别求解即可.
【解答】解:经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线:
当截距为0时,直线过原点:y=2x;
当斜率为1时,直线方程:x﹣y+1=0;
当斜率为﹣1时,直线方程:x+y﹣3=0.
综上所述,直线方程为y=2x或x+y﹣3=0或x﹣y+1=0.
故选D.
5.某产品的广告费用x与销售额y的不完整统计数据如表:
广告费用x(万元)
3
4
5
销售额y(万元)
22
28
m
若已知回归直线方程为=9x﹣6,则表中m的值为( )
A.40
B.39
C.38
D.37
【考点】线性回归方程.
【分析】求出数据中心(,),代入回归方程解出m.
【解答】解:由题意,回归方程过样本平均数点(,),可求出=4
代入得;
=36﹣6=30,
则30=,∴m=40.
故选:A.
6.已知约束条件若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
A.0<a<
B.a≥
C.a>
D.0<a<
【考点】简单线性规划的应用.
【分析】先根据约束条件画出可行域,再利用几何意义求最值的方法,利用直线斜率之间的关系,只需求出直线z=x+ay的斜率的取值范围即可.
【解答】解:画出已知约束条件的可行域为△ABC内部(包括边界),
如图,易知当a=0时,不符合题意;
当a>0时,由目标函数z=x+ay得y=﹣x+,
则由题意得﹣3=kAC<﹣<0,故a>.
综上所述,a>.
故选C.
7.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )
A.24
B.20
C.0
D.﹣4
【考点】直线的一般式方程与直线的垂直关系.
【分析】先由两直线平行斜率相等,求出m,第一直线的方程确定了,把垂足坐标代入,可求p,垂足坐标确定了.
把垂足坐标代入第二条直线的方程可得
n,进而求得m﹣n+p的值.
【解答】解:∵直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,
∴×=﹣1,
∴m=10,
直线mx+4y﹣2=0
即
5x+2y﹣1=0,垂足(1,p)代入得,5+2p﹣1=0,∴p=﹣2.
把P(1,﹣2)代入2x﹣5y+n=0,可得
n=﹣12,
∴m﹣n+p=20,
故选B.
8.如图,给出的是计算×××…×的值的程序框图,其中判断框内不能填入的是( )
A.i≤2017?
B.i<2018?
C.i≤2015?
D.i≤2016?
【考点】程序框图.
【分析】根据程序运行后输出的算式,分析倒数第一圈,即i=2016时满足条件,i=2018不满足循环条件;由此可得判断框内不能填入的选项.
【解答】解:∵程序运行后输出的是S=×××…×的值,
∴分析倒数第一圈,i=2016时,满足条件,执行循环S=×××…×,
i=i+2=2018,此时不满足条件,终止循环,输出S=×××…×的值;
∴判断框内能填入“i≤2017?”,“i<2018?”,“i≤2016?”,
不能填入“i≤2015?”.
故选:C.
9.“m=1”是“直线mx+y﹣2=0与直线x+my+1﹣m=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】直线的一般式方程与直线的平行关系.
【分析】根据充分必要条件的定义,分别进行判断从而得到结论.
【解答】解:m=1时,直线mx+y﹣2=0与直线x+my+1﹣m=0相互平行,是充分条件,
若直线mx+y+2=0与直线x+my+1﹣m=0相互平行,
则,解得:m=1,是必要条件,
故选:C.
10.一个几何体的三视图如图所示,则该几何体的体积为( )
A.
B.
C.
D.
【考点】由三视图求面积、体积.
【分析】三视图复原的几何体是一个半圆锥和圆柱的组合体,根据三视图的数据,求出半圆锥和圆柱的体积,相加可得答案.
【解答】解:三视图复原的几何体是一个半圆锥和圆柱的组合体,
它们的底面直径均为2,故底面半径为1,
圆柱的高为1,半圆锥的高为2,
故圆柱的体积为:π×12×1=π,
半圆锥的体积为:×=,
故该几何体的体积V=π+=,
故选:B
11.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是( )
A.若m、n都平行于平面α,则m、n一定不是相交直线
B.若m、n都垂直于平面α,则m、n一定是平行直线
C.已知α、β互相平行,m、n互相平行,若m∥α,则n∥β
D.若m、n在平面α内的射影互相平行,则m、n互相平行
【考点】命题的真假判断与应用;空间中直线与直线之间的位置关系;空间中直线与平面之间的位置关系;平面与平面之间的位置关系.
【分析】A,平行于同一平面的两条直线可能相交,也可能平行;
B,垂直于同一平面的两条直线一定平行;
C,α、β互相平行,m、n互相平行,若m∥α,则n∥β或
n β;
D,m、n在平面α内的射影互相平行,则m、n互相平行或相交,
【解答】解:对于A,平行于同一平面的两条直线可能相交,也可能平行,故错;
对于B,垂直于同一平面的两条直线一定平行,故正确;
对于C,α、β互相平行,m、n互相平行,若m∥α,则n∥β或
n β,故错;
对于D,m、n在平面α内的射影互相平行,则m、n互相平行或相交,故错,
故选:B.
12.在平面直角坐标系中,两点P1(x1,y
( http: / / www.21cnjy.com )1),P2(x2,y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.则平面内与x轴上两个不同的定点F1,F2的“L﹣距离”之和等于定值(大于|F1F2|)的点的轨迹可以是( )
A.
B.
C.
D.
【考点】轨迹方程.
【分析】设出F1,F2的坐标,在设出动点M的坐标,由新定义列式后分类讨论去绝对值,然后结合选项得答案.
【解答】解:设F1(﹣c,0),F2(c,0),
再设动点M(x,y),动点到定点F1,F2的“L﹣距离”之和等于m(m>2c>0),
由题意可得:|x+c|+|y|+|x﹣c|+|y|=m,
即|x+c|+|x﹣c|+2|y|=m.
当x<﹣c,y≥0时,方程化为2x﹣2y+m=0;
当x<﹣c,y<0时,方程化为2x+2y+m=0;
当﹣c≤x<c,y≥0时,方程化为y=;
当﹣c≤x<c,y<0时,方程化为y=c﹣;
当x≥c,y≥0时,方程化为2x+2y﹣m=0;
当x≥c,y<0时,方程化为2x﹣2y﹣m=0.
结合题目中给出的四个选项可知,选项A中的图象符合要求.
故选:A.
二、填空题(本大题共4小题,每小题5分,共20分)
13.在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),则A,B两点间的距离为 5 .
【考点】空间两点间的距离公式.
【分析】利用空间中两点间的距离公式求解.
【解答】解:∵在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),
∴A,B两点间的距离:
|AB|==5,
故答案为:5.
14.为了对某课题进行研究
( http: / / www.21cnjy.com ),用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人).则x= 1 ,y= 3 ;
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
若从高校B,C抽取的人中选2人作专题发言,则这2人都来自高校C的概率= .
【考点】频率分布表.
【分析】由已知得,由此能求出x=1,y=3,从高校B,C抽取的人中选2人作专题发言,基本事件总数n==10,这2人都来自高校C包含基本事件个数m==3,由此能求出这2人都来自高校C的概率.
【解答】解:由已知得,
解得x=1,y=3,
从高校B,C抽取的人中选2人作专题发言,
基本事件总数n==10,
这2人都来自高校C包含基本事件个数m==3,
∴这2人都来自高校C的概率:p=.
故答案为:1,3,.
15.将某选手的6个得分去掉1个最高分
( http: / / www.21cnjy.com ),去掉一个最低分,4个剩余分数的平均分为91.现场作的6个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:则4个剩余分数的方差为 .
【考点】茎叶图.
【分析】根据茎叶图求出平均数,即可计算方差的大小.
【解答】解:去掉最低分87,若x≥3,则90+x被去掉,
此时剩余的分数为90,90,91,93,平均数为91,
满足条件,
此时对应的方差为
[(90﹣91)2+(90﹣91)2+(91﹣91)2+(93﹣91)2]=(1+1+4)=,
故答案为:.
16.已知双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),则a= 1 ,b= 2 .
【考点】双曲线的标准方程.
【分析】由双曲的一条渐近线为2x+y=0,一个焦点为(,0),列出方程组,由此能出a,b.
【解答】解:∵双曲线﹣=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),
∴,
解得a=1,b=2.
故答案为:1,2.
三、解答题(17小题10分,18-22小题每题12分;共70分)
17.我国是世界上严重缺水的国家,某市
( http: / / www.21cnjy.com )为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
【考点】频率分布直方图;众数、中位数、平均数.
【分析】(I)先根据频率分布直方图中的频率等于纵坐标乘以组距求出9个矩形的面积即频率,再根据直方图的总频率为1求出a的值;
(II)根据已知中的频率分布直方图先求出月均用水量不低于3吨的频率,结合样本容量为30万,进而得解.
(Ⅲ)根据频率分布直方图,求出使直方图中左右两边频率相等对应的横坐标的值.
【解答】解:(I)∵1=(0.08
( http: / / www.21cnjy.com )+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5,整理可得:2=1.4+2a,
∴解得:a=0.3.
(II)估计全市居民中月均用水量不低于3吨的人数为3.6万,理由如下:
由已知中的频率分布直方图可得月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12,
又样本容量=30万,
则样本中月均用水量不低于3吨的户数为30×0.12=3.6万.
(Ⅲ)根据频率分布直方图,得;
0.08×0.5+0.16×0.5+0.30×0.5+0.40×0.5=0.47<0.5,
0.47+0.5×0.52=0.73>0.5,
∴中位数应在(2,2.5]组内,设出未知数x,
令0.08×0.5+0.16×0.5+0.30×0.5+0.4×0.5+0.5×x=0.5,
解得x=0.06;
∴中位数是2+0.06=2.06.
18.已知命题p: x∈R,不等式恒成立,命题q:椭圆的焦点在x轴上.若命题p∨q为真命题,求实数m的取值范围.
【考点】复合命题的真假.
【分析】分别求出p,q为真时的m的范围,根据p∨q为假命题,得到关于m的不等式组,解出即可.
【解答】解:p真:,∴…
q真:m﹣1>3﹣m>0∴2<m<3…6分
若p∨q为假命题,则…
∴实数m的取值范围是…
19.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
【考点】解三角形.
【分析】(Ⅰ)已知等式利用正弦定理化简,
( http: / / www.21cnjy.com )整理后利用两角和与差的正弦函数公式及诱导公式化简,根据sinC不为0求出cosC的值,即可确定出出C的度数;
(2)利用余弦定理列出关系式,利用三角形面积公式列出关系式,求出a+b的值,即可求△ABC的周长.
【解答】解:(Ⅰ)已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
∵sinC≠0,sin(A+B)=sinC
∴cosC=,
又0<C<π,
∴C=;
(Ⅱ)由余弦定理得7=a2+b2﹣2ab ,
∴(a+b)2﹣3ab=7,
∵S=absinC=ab=,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周长为5+.
20.如图,四棱锥P﹣ABCD中,P
( http: / / www.21cnjy.com )A⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.
【分析】(Ⅰ)取BC中点E,连结EN,EM,得NE是△PBC的中位线,推导出四边形ABEM是平行四边形,由此能证明MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,NF是△
( http: / / www.21cnjy.com )PAC的中位线,推导出NF⊥面ABCD,延长BC至G,使得CG=AM,连结GM,则四边形AGCM是平行四边形,由此能求出四面体N﹣BCM的体积.
【解答】证明:(Ⅰ)取BC中点E,连结EN,EM,
∵N为PC的中点,∴NE是△PBC的中位线
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN 平面NEM,∴MN∥平面PAB.
解:(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF==2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AMCG,∴四边形AGCM是平行四边形,
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=,
∴S△BCM===2,
∴四面体N﹣BCM的体积VN﹣BCM===.
21.袋子中放有大小和形状相同
( http: / / www.21cnjy.com )的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(I)求n的值;
(II)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x,y,求事件“x2+y2>(a﹣b)2恒成立”的概率.
【考点】几何概型;古典概型及其概率计算公式.
【分析】(Ⅰ)利用从袋子中随机抽取1个小球,取到标号是2的小球的概率是,确定n的值.
(Ⅱ)①从袋子中不放回地随机抽取2个球
( http: / / www.21cnjy.com ),共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率.②记“x2+y2>(a﹣b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型可求得结论.
【解答】解:(Ⅰ)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是可得,
解得n=2.
(Ⅱ)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,则P(A)=.
②记“x2+y2>(a﹣b)2恒成立”为事
( http: / / www.21cnjy.com )件B,则事件B等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},
所以P(B)=1﹣.
22.已知椭圆+=1(a>b>0)的左右焦点分别为F1和F2,由4个点M(﹣a,b)、N(a,b)、F2和F1组成了一个高为,面积为3的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A、B,求△F2AB面积的最大值.
【考点】直线与圆锥曲线的关系;椭圆的标准方程.
【分析】解:(1)由题意知b=,
=3,即a+c=3①,又a2=3+c2②,联立①②解得a,c,;
(2)设A(x1,y1),B(x2,y
( http: / / www.21cnjy.com )2),过点F1的直线方程为x=ky﹣1,代入椭圆方程消掉x得y的二次方程,△F2AB的面积S==|y1﹣y2|=,由韦达定理代入面积表达式变为k的函数,适当变形借助函数单调性即可求得S的最大值;
【解答】解:(1)由题意知b=,
=3,所以a+c=3①,
又a2=b2+c2,即a2=3+c2②,
联立①②解得a=2,c=1,
所以椭圆方程为:;
(2)由(1)知F1(﹣1,0),
设A(x1,y1),B(x2,y2),过点F1的直线方程为x=ky﹣1,
由得(3k2+4)y2﹣6ky﹣9=0,△>0成立,
且,,
△F2AB的面积S==|y1﹣y2|=
==12=,
又k2≥0,所以递增,
所以9+1+6=16,
所以≤=3,当且仅当k=0时取得等号,
所以△F2AB面积的最大值为3.
2017年3月7日
