17.2.2 函数的图象——函数图象的应用 同步练习
文档属性
| 名称 | 17.2.2 函数的图象——函数图象的应用 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 545.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-07 22:36:36 | ||
图片预览



文档简介
17.2.2 函数的图象——函数图象的应用
核心笔记: 从图象中获取信息:要从图象中获取信息,首先必须明确图象表示的是哪两个变量之间的关系及图象上的点所表示的意义.
基础训练
1.小强的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会儿太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
2.如图是韩老师早晨出门散步时离家的距离(y)与时间(x)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是图中的( )2·1·c·n·j·y
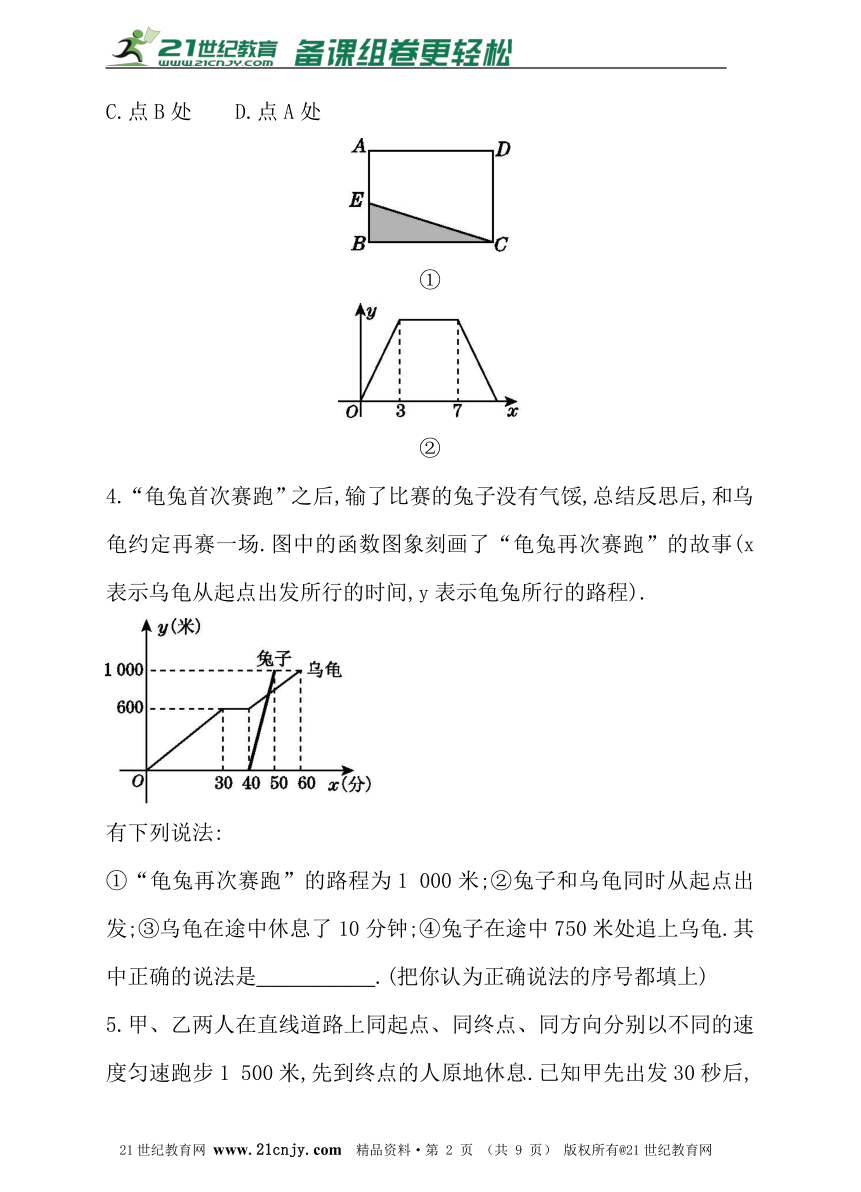
3.如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C的方向运动至点C处停止,设点E运动的路程为x,△BCE的面积为y,如果y关于x的函数图象如图②所示,则当x=7时,点E应运动到( )
A.点C处 B.点D处
C.点B处 D.点A处
①
②
4.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y表示龟兔所行的路程).
有下列说法:
①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是___________.(把你认为正确说法的序号都填上)?
5.甲、乙两人在直线道路上同起点、同终点、同方向分别以不同的速度匀速跑步1 500米,先到终点的人原地休息.已知甲先出发30秒后,乙才出发.在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.则乙到终点时,甲距终点的距离是___________米.21世纪教育网版权所有
6.一辆汽车的速度随时间变化的情况如图所示:
(1)这辆汽车的最高速度是多少?
(2)汽车在行驶了多长时间后停了下来,停了多长时间?
(3)汽车在第一次匀速行驶(速度不变)时共用了几分钟?速度是多少?在这段时间内,它走了多远?
培优提升
1.伟伟从学校匀速回家,刚到家发现当晚要完成的试卷忘记在学校,于是马上以更快的速度匀速原路返回学校,这一情境中,速度v和时间t的函数图象(不考虑图象端点情况)大致是图中的( )
2.小亮每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分30米的速度行走了450米,为了不迟到他加快了速度,以每分45米的速度行走完剩下的路程,那么小亮行走过的路程s(米)与他行走的时间t(分)之间的函数关系用图象表示正确的是( )
3.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和乙骑行时间t(h)之间的函数关系如图所示.给出下列说法:www.21-cn-jy.com
①他们都骑行了20 km;②乙在途中停留了0.5 h;
③甲、乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有( ) 【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
4.如图是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象,观察图象,从中得到如下信息:①学校离小明家1 000米;②小明用了10分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快.其中正确的有 (填序号).?
5.甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示,那么可以知道:
(1)这是一次 米的赛跑;?
(2)甲、乙两人中先到达终点的是 ;?
(3)乙在这次赛跑中的平均速度为 .?
6.如图,曲线是某一函数的图象,根据图象回答:
(1)当x为何值时,y>0?
(2)当x为何值时,y=0?
(3)当x为何值时,y<0?
(4)当函数值y取最小值为-1时,自变量x的值为多少?
7.如图是一对变量满足的函数关系的图象.有下列3个不同的问题情境:
①小明骑车以400米/分的速度匀速骑了5分,在原地休息了4分,然后以500米/分的速度匀速骑回出发地,设时间为x分,离出发地的距离为y千米;21教育网
②有一个容积为6升的开口空桶,小亮以1.2升/分的速度匀速向这个空桶注水,注5分后停止,等4分后,再以2升/分的速度匀速倒空桶中的水,设时间为x分,桶内的水量为y升;21·cn·jy·com
③长方形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC、边CD、边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0.其中,符合图中所示函数关系的问题情境的个数为( )www-2-1-cnjy-com
A.0 B.1 C.2 D.3
参考答案
【基础训练】
1.【答案】B 2.【答案】D
3.【答案】B
解:当E在AB上运动时,△BCE的面积不断增大;
当E在AD上运动时,BC一定,BC边上的高不变,此时面积不变;
当E在DC上运动时,△BCE的面积不断减小.
∴当x=7时,点E应运动到点D处.
4.【答案】①③④
5.【答案】175
解:由图可看出,v甲==2.5(米/秒),v乙-v甲==0.5(米/秒),所以v乙=2.5+0.5=3(米/秒).t乙==500(秒),所以乙到终点时,甲距终点的距离为1 500-(500+30)×2.5=175(米).21·世纪*教育网
6.解:(1)这辆汽车的最高速度是120千米/时.
(2)汽车在行驶了10分钟后停了下来,停了12-10=2(分钟).
(3)汽车在第一次匀速行驶时共用了6-2=4(分钟).速度是90千米/时.在这段时间内,它走了4÷60×90=6(千米).2-1-c-n-j-y
【培优提升】
1.【答案】A
2.【答案】D
解:小亮行走过的路程s(米)应随他行走的时间t(分)的增大而增大,因而选项A、B一定错误;他从家去上学时以每分30米的速度行走了450米,所用时间应是15分,因而选项C错误;行走了450米后,为了不迟到,他加快了速度,后面一段图象陡一些,选项D正确.
3.【答案】B
解:由图象可获取的信息是:他们都骑行了20 km;乙在途中停留了0.5 h;相遇后,甲的速度大于乙的速度;甲比乙早0.5 h到达目的地.所以①②正确.21*cnjy*com
4.【答案】①④ 5.【答案】(1)100 (2)甲 (3)8米/秒
6.解:(1)-2(2)x=-2或2或4.
(3)2(4)x=3.
解:当图象位于x轴上方时,y>0;
当图象与x轴相交时,y=0;
当图象位于x轴下方时,y<0;
图象最高点处,函数取最大值;
图象最低点处,函数取最小值.
7.【答案】C
解:①小明骑车以400米/分的速度匀速骑了5分,
所走路程为2千米,与图象不符合.②小亮以1.2升/分的速度向空桶注水,注5分后停止,注水量为1.2×5=6(升);等4分,这段时间桶内的水量不变;再以2升/分的速度匀速倒空桶中的水,则3分后桶内的水量为0升,符合函数图象.③如图所示,当点P在AC上运动时,S△ABP一直增加,当点P运动到点C时,S△ABP=6,易知这段路程为5;当点P在CD上运动时,S△ABP不变,这段路程为4;当点P在DA上运动时,S△ABP不断减小,这段路程为3,符合函数图象.综上可得,符合题图中所示函数关系的问题情境的个数为2,故选C.21cnjy.com
核心笔记: 从图象中获取信息:要从图象中获取信息,首先必须明确图象表示的是哪两个变量之间的关系及图象上的点所表示的意义.
基础训练
1.小强的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会儿太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
2.如图是韩老师早晨出门散步时离家的距离(y)与时间(x)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是图中的( )2·1·c·n·j·y
3.如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C的方向运动至点C处停止,设点E运动的路程为x,△BCE的面积为y,如果y关于x的函数图象如图②所示,则当x=7时,点E应运动到( )
A.点C处 B.点D处
C.点B处 D.点A处
①
②
4.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y表示龟兔所行的路程).
有下列说法:
①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是___________.(把你认为正确说法的序号都填上)?
5.甲、乙两人在直线道路上同起点、同终点、同方向分别以不同的速度匀速跑步1 500米,先到终点的人原地休息.已知甲先出发30秒后,乙才出发.在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.则乙到终点时,甲距终点的距离是___________米.21世纪教育网版权所有
6.一辆汽车的速度随时间变化的情况如图所示:
(1)这辆汽车的最高速度是多少?
(2)汽车在行驶了多长时间后停了下来,停了多长时间?
(3)汽车在第一次匀速行驶(速度不变)时共用了几分钟?速度是多少?在这段时间内,它走了多远?
培优提升
1.伟伟从学校匀速回家,刚到家发现当晚要完成的试卷忘记在学校,于是马上以更快的速度匀速原路返回学校,这一情境中,速度v和时间t的函数图象(不考虑图象端点情况)大致是图中的( )
2.小亮每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分30米的速度行走了450米,为了不迟到他加快了速度,以每分45米的速度行走完剩下的路程,那么小亮行走过的路程s(米)与他行走的时间t(分)之间的函数关系用图象表示正确的是( )
3.甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和乙骑行时间t(h)之间的函数关系如图所示.给出下列说法:www.21-cn-jy.com
①他们都骑行了20 km;②乙在途中停留了0.5 h;
③甲、乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.根据图象信息,以上说法正确的有( ) 【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
4.如图是小明从学校到家里行进的路程s(米)与时间t(分)的函数图象,观察图象,从中得到如下信息:①学校离小明家1 000米;②小明用了10分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快.其中正确的有 (填序号).?
5.甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示,那么可以知道:
(1)这是一次 米的赛跑;?
(2)甲、乙两人中先到达终点的是 ;?
(3)乙在这次赛跑中的平均速度为 .?
6.如图,曲线是某一函数的图象,根据图象回答:
(1)当x为何值时,y>0?
(2)当x为何值时,y=0?
(3)当x为何值时,y<0?
(4)当函数值y取最小值为-1时,自变量x的值为多少?
7.如图是一对变量满足的函数关系的图象.有下列3个不同的问题情境:
①小明骑车以400米/分的速度匀速骑了5分,在原地休息了4分,然后以500米/分的速度匀速骑回出发地,设时间为x分,离出发地的距离为y千米;21教育网
②有一个容积为6升的开口空桶,小亮以1.2升/分的速度匀速向这个空桶注水,注5分后停止,等4分后,再以2升/分的速度匀速倒空桶中的水,设时间为x分,桶内的水量为y升;21·cn·jy·com
③长方形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC、边CD、边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0.其中,符合图中所示函数关系的问题情境的个数为( )www-2-1-cnjy-com
A.0 B.1 C.2 D.3
参考答案
【基础训练】
1.【答案】B 2.【答案】D
3.【答案】B
解:当E在AB上运动时,△BCE的面积不断增大;
当E在AD上运动时,BC一定,BC边上的高不变,此时面积不变;
当E在DC上运动时,△BCE的面积不断减小.
∴当x=7时,点E应运动到点D处.
4.【答案】①③④
5.【答案】175
解:由图可看出,v甲==2.5(米/秒),v乙-v甲==0.5(米/秒),所以v乙=2.5+0.5=3(米/秒).t乙==500(秒),所以乙到终点时,甲距终点的距离为1 500-(500+30)×2.5=175(米).21·世纪*教育网
6.解:(1)这辆汽车的最高速度是120千米/时.
(2)汽车在行驶了10分钟后停了下来,停了12-10=2(分钟).
(3)汽车在第一次匀速行驶时共用了6-2=4(分钟).速度是90千米/时.在这段时间内,它走了4÷60×90=6(千米).2-1-c-n-j-y
【培优提升】
1.【答案】A
2.【答案】D
解:小亮行走过的路程s(米)应随他行走的时间t(分)的增大而增大,因而选项A、B一定错误;他从家去上学时以每分30米的速度行走了450米,所用时间应是15分,因而选项C错误;行走了450米后,为了不迟到,他加快了速度,后面一段图象陡一些,选项D正确.
3.【答案】B
解:由图象可获取的信息是:他们都骑行了20 km;乙在途中停留了0.5 h;相遇后,甲的速度大于乙的速度;甲比乙早0.5 h到达目的地.所以①②正确.21*cnjy*com
4.【答案】①④ 5.【答案】(1)100 (2)甲 (3)8米/秒
6.解:(1)-2
(3)2
解:当图象位于x轴上方时,y>0;
当图象与x轴相交时,y=0;
当图象位于x轴下方时,y<0;
图象最高点处,函数取最大值;
图象最低点处,函数取最小值.
7.【答案】C
解:①小明骑车以400米/分的速度匀速骑了5分,
所走路程为2千米,与图象不符合.②小亮以1.2升/分的速度向空桶注水,注5分后停止,注水量为1.2×5=6(升);等4分,这段时间桶内的水量不变;再以2升/分的速度匀速倒空桶中的水,则3分后桶内的水量为0升,符合函数图象.③如图所示,当点P在AC上运动时,S△ABP一直增加,当点P运动到点C时,S△ABP=6,易知这段路程为5;当点P在CD上运动时,S△ABP不变,这段路程为4;当点P在DA上运动时,S△ABP不断减小,这段路程为3,符合函数图象.综上可得,符合题图中所示函数关系的问题情境的个数为2,故选C.21cnjy.com
