9.1.2不等式的性质 课件

课件32张PPT。第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质第1课时 不等式的性质1.理解并掌握不等式的基本性质;
2.通过实例操作,培养学生观察、分析、比较的能力,
会用不等式的基本性质解简单的不等式.(重点、难点)学习目标前面我们已经学习过等式的基本性质
（1）等式的两边都加上（或都减去）同一个
数或同一个整式，等式仍然成立.
（2）等式的两边都乘以（或除以）一个不为0
的数，等式仍然成立.
猜想 ：不等式也具有同样的性质吗？导入新课复习引入讲授新课 用不等号填空：（1）5 3 ； 5+2 3+2 ；5-2 3-2 .> > > < < < 合作与交流自己再写一个不等式，分别在它的两边都加（或减）同一个正数或负数，看看有怎样的结果？与同桌互相交流，你们发现了什么规律？ 不等式基本性质1 不等式的两边都加上（或都减去）同一个数或（式），不等号的方向不变. 即，如果a>b，那么 a + c > b + c，且 a-c>b-c.一般地，不等式具有如下性质：一、不等式基本性质1 用不等号填空：（1）5 3 ； 5×2 3×2 ；5÷2 3÷2 .> > > < < < 合作与交流自己再写一个不等式，分别在它的两边都乘（或除以）同一个正数，看看有怎样的结果？与同桌互相交流，你们发现了什么规律？ 不等式基本性质2 不等式的两边都乘（或除以）同一个正数，不等号的方向不变.一般地，不等式还有如下性质：二、不等式基本性质2 用不等号填空：（1）5 3 ； 5×(－2) 3×2 ；5÷(-2) 3÷(-2) .> < < < > > 合作与交流自己再写一个不等式，分别在它的两边都乘（或除以）同一个负数，看看有怎样的结果？与同桌互相交流，你们发现了什么规律？ 不等式基本性质3 不等式的两边都乘（或除以）同一个负数，不等号的方向改变.三、不等式基本性质3一般地，不等式还有如下性质： （1）如果a＞b，那么ac＞bc.
（2）如果a＞b，那么ac2＞bc2.
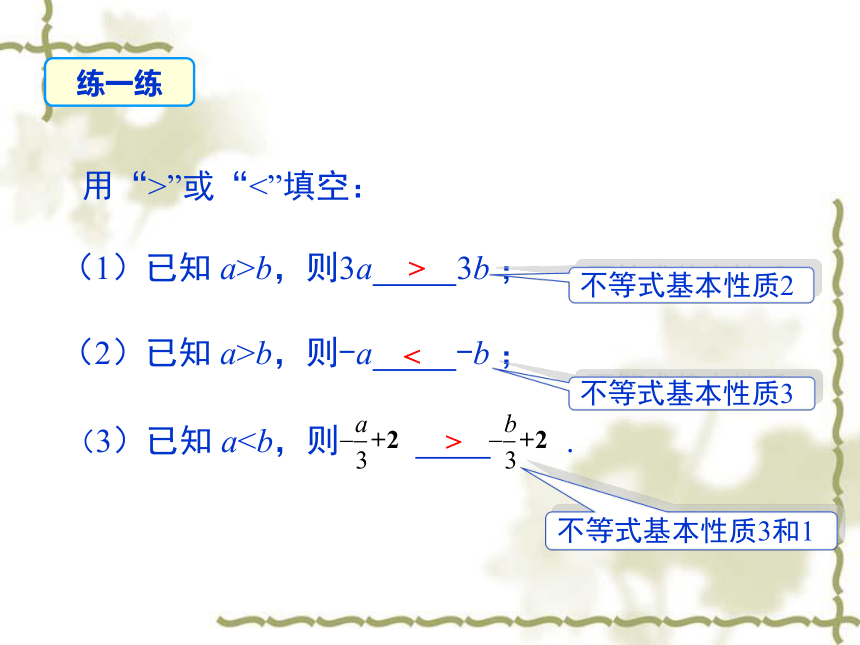
（3）如果ac2＞bc2，那么a＞b.你能用不等式的基本性质判断下列说法的正误吗？××√ 因为c≠0，所以c2＞0.当c≤0时，不成立.当c=0时，不成立. 不等式的基本性质与等式的基本性质有什么相同点和不同点？ 用“>”或“<”填空：（1）已知 a>b，则3a 3b ；（2）已知 a>b，则-a -b ；不等式基本性质2>不等式基本性质3<不等式基本性质3和1 > 练一练例2 利用不等式的性质解下列不等式：
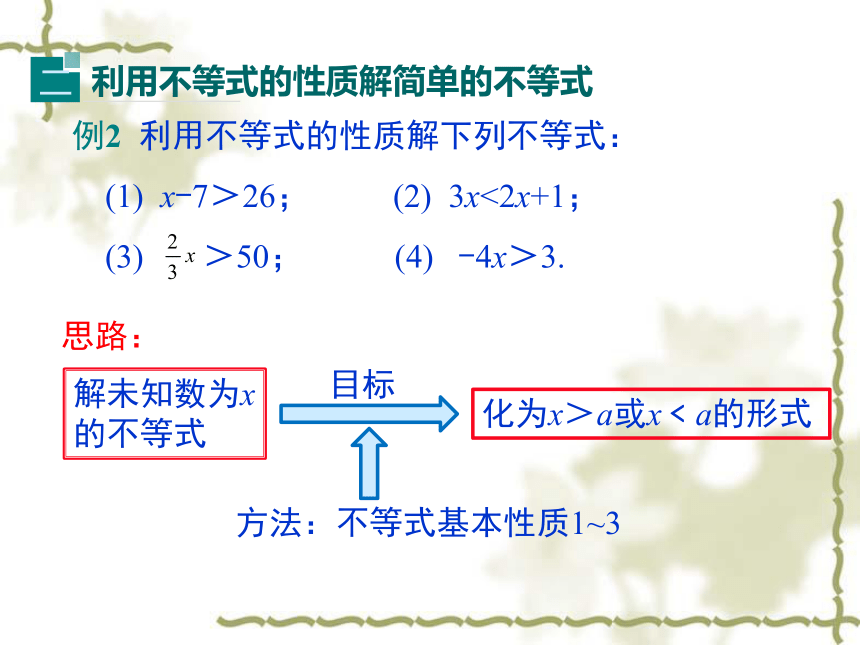
(1) x-7＞26； (2) 3x<2x+1；
(3) ＞50；　　 (4) -4x＞3.　　　　解未知数为x的不等式化为x＞a或x﹤a的形式目标方法：不等式基本性质1~3思路：解 (1)为了使不等式x-7＞26中不等号的一边变为x，
根据不等式的性质1，不等式两边都加7，不
等号的方向不变,得 x-7+7﹥26+7，即x﹥33.这个不等式的解集在数轴上的表示如图所示：　(2)为了使不等式3x<2x+1中不等号的一边变为x，根
据_____________，不等式两边都减去____，不等
号的方向_____，得 .3x-2x﹤2x+1-2x ，即 x﹤1这个不等式的解集在数轴上的表示如图所示：不等式性质12x不变(3)为了使不等式 ﹥50中不等号的一边变为x，根据
不等式的性质2，不等式的两边都除以　不等号的
方向不变，得x﹥75.这个不等式的解集在数轴上的表示如图所示:(4)为了使不等式-4x﹥3中的不等号的一边变为x，
根据______________，不等式两边都除以____，
不等号的方向______，得x﹤- .这个不等式的解集在数轴上的表示如图所示：不等式的性质3-4改变 下面是某同学根据不等式的性质做的一道题：在不等式-4x+5>9的两边都减去5，得 -4x > 4在不等式-4x> 4的两边都除以-4，得 x > -1 请问他做对了吗？如果不对，请改正.不对x < -1 1. 已知a < b，用“>”或“<”填空： （1）a +12 b +12 ； （2）b-10 a -10 .<>当堂练习解：x < 2解：x < 62. 把下列不等式化为x>a或x 3(1)x-5 > -1(3)7x < 6x-6x＞4 x<-6课堂小结不等式的基本性质不等式基本性质2不等式基本性质3→→应用不等式的基本性质1如果a>b，那么a+c>b+c，a-c>b-c→第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质 第2课时 含“≤”“≥”的不等式1.进一步了解不等式的概念，认识几种不等号的含义;
2.学会并准确运用不等式表示数量关系，形成在表达
中渗透数形结合的思想．（重点、难点）学习目标问题 前面学过哪几种形式的不等式？ 学过用符号“<”“>”或“≠ ”连接的式子叫做不等式.思考 写出下列图片信息中的含义：导入新课回顾与思考问题 一辆轿车在一条规定车速不低于60km/h，且不高于100 km/h的高速公路上行驶，如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢？根据路程与速度、时间之间的关系可得：s≥60x，且s≤100x.讲授新课常用的表示不等关系的关键词语及对应的不等号﹤＞≥≤＞0﹤0≥0≤0 我们把用不等号（>,<,≥,≤,≠）连接而成的式子叫作不等式.其中“≥”读作大于等于，“≤”读作小于等于.不等式的概念 例 某长方体形状的容器长5cm,宽10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位：cm3)表示新注入水的体积，写出V的取值范围.典例精析解：新注入水的体积V与原有水的体积的和不能超过
容器的容积，即V+3×5×3≤3×5×10解得 V≤105 又由于新注入水的体积不能是负数，因此，V的取值范围是V≥0并且V≤105.在数轴上表示V的取值范围如图利用不等式的性质解不等式的注意事项2.要注意区分“大于” “不大于”“小于”“不小于”
等数学语言的使用，并把这些表示不等关系的语言用数
学符号准确地表达出来.3.在数轴上表示解集应注意的问题：方向、空心或实心.1.在运用性质3时,要特别注意：不等式两边都乘以或除以
同一个负数时，要改变不等号的方向. 1.用不等式表示下列语句并写出解集，并在数轴
上表示解集.（1）x的3倍大于或等于1；（2）x与3的和不小于6；（3）y与1的差不大于0；（4）y的 小于或等于-2. 分析：本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用“ ≥”表示；不大于、小于或等于都用“≤”表示. 当堂练习解：(1)3x≥1, 解集是x≥ ;(2)x+3≥6, 解集是x≥3;(3)y-1≤0, 解集是y≤1;2.小希就读的学校上午第一节课上课时间是8点开始.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希上午几点从家里出发才能保证不迟到？ 解：设小希上午x点从家里出发才能不迟到，根据题意得 答：小希上午7:48前时从家里出发才能不迟到.≤8解得x≤一个概念：不等式两种思想：数学建模、类比等式三个注意：一要注意“负数”、“非负数”、“不大于”、“不小于”等关键词语的含义；
二要注意仔细审题，正确列出不等式；
三要注意观察生活，让数学服务生活。课堂小结