9.3一元一次不等式组 课件

课件20张PPT。第九章 不等式与不等式组9.3 一元一次不等式组1.通过具体操作，在解一元一次不等式组的过程中
形成正确的解不等式的思路与方法;(重点、难点)
2.掌握将一元一次不等式组的解集在数轴上正确的
表示.
3.会利用一元一次不等式组解决实际问题.(重点、难点)学习目标导入新课 一个长方形足球场的宽为70m，如果它的周长大于350m，面积小于7630m2，求这个足球场的长的取值范围.观察与思考讲授新课 如果设足球场的长为x m，
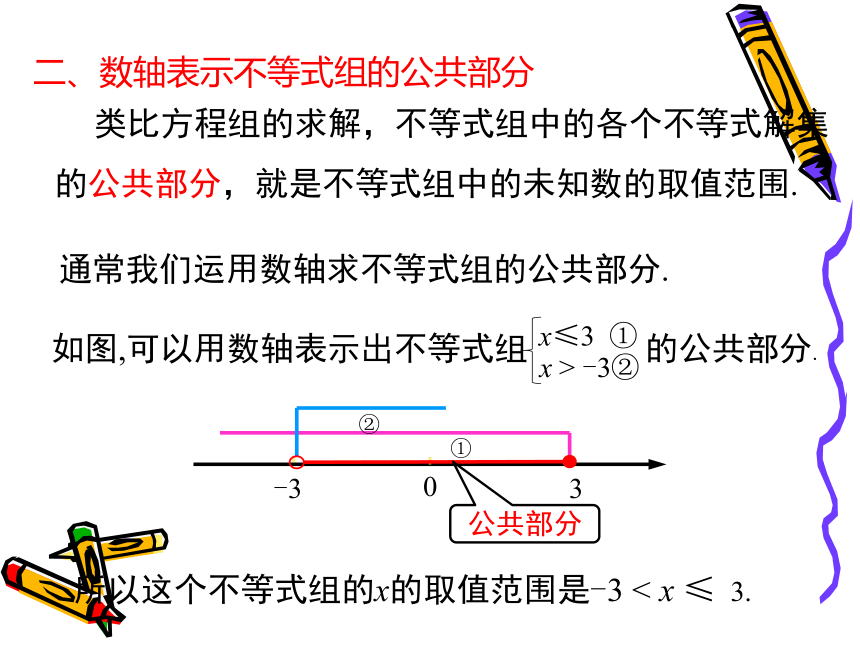
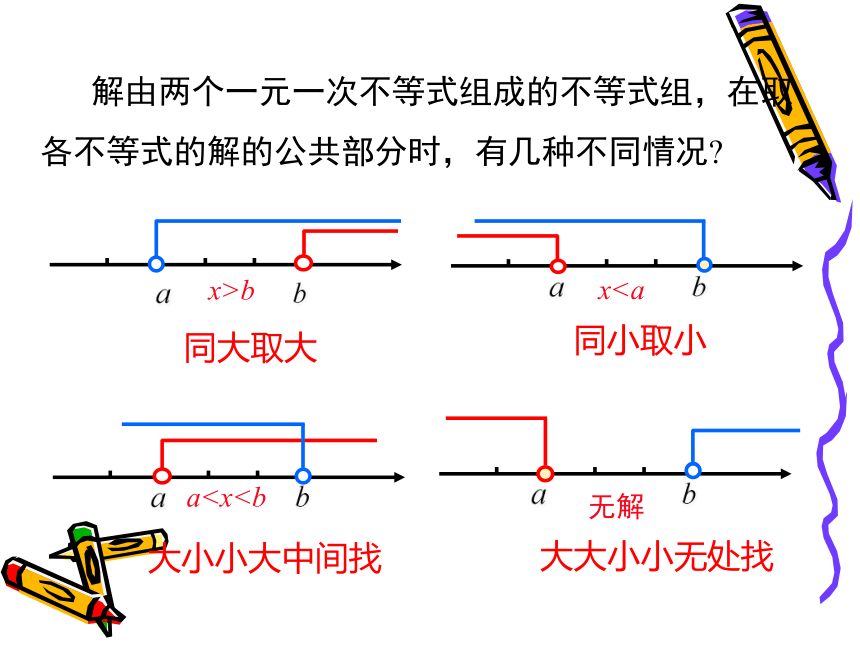
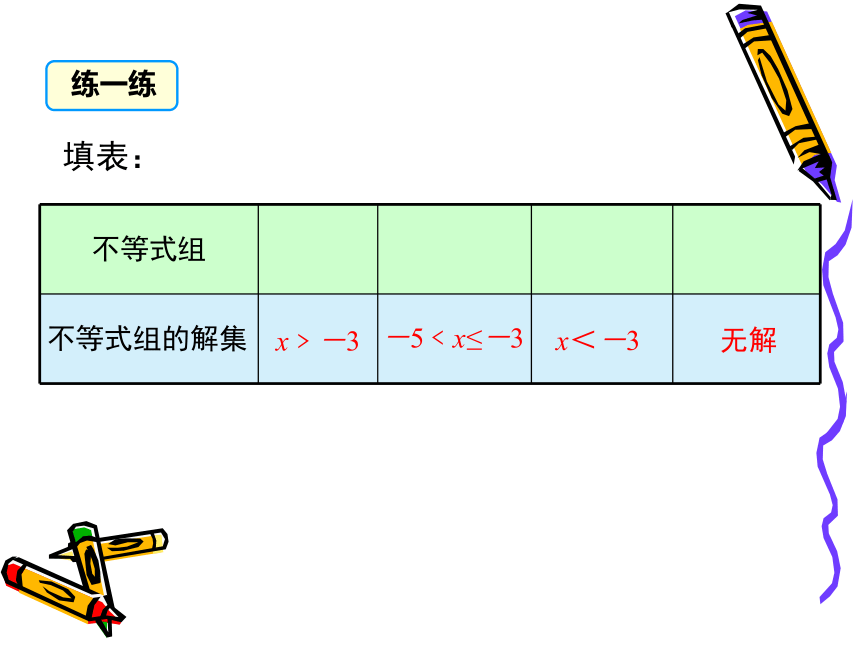
那么它的周长就是2(x+70)m，面积为70x m2. 根据已知条件，我们知道x的取值范围要使2(x+70)>350 和70x<7630这两个不等式同时成立.用大括号把上述两个不等式联立起来，得一、一元一次不等式组的概念思考：怎样确定上面的不等式组中x的取值范围呢？ 类比方程组的求解，不等式组中的各个不等式解集的公共部分，就是不等式组中的未知数的取值范围. 通常我们运用数轴求不等式组的公共部分.公共部分所以这个不等式组的x的取值范围是-3 < x ≤ 3.二、数轴表示不等式组的公共部分 解由两个一元一次不等式组成的不等式组，在取各不等式的解的公共部分时，有几种不同情况? 同大取大 同小取小 大小小大中间找 大大小小无处找x>bxx＜-3，所以这个不等式组的解集是 x＜－3.典例精析例2 解不等式组： 解 解不等式①，得 x ＜－2. 解不等式②，得 x ＞3. 把不等式①、②的解集在数轴上表示出来，
如图： 由图可以看出这两个不等式的解集没有公共部分.
所以，这个不等式组无解.例3 x取哪些整数值时，不等式
2-x≥0
与
都成立？解：不等式组
解不等式①，得x≤2，
解不等式②，得x＞－3.
故此不等式组的解集为－3＜x≤2，x可取的整数
值为－2，－1，0，1，2.①
② 3个小组计划在10天内生产500件产品（每天生产量相同），按原先的生产速度，不能完成任务；如果每个小组每天比原先生产1件产品，就能提前完成任务.每个小组原先每天生产多少件产品？合作与交流解：设每个小组原先每天生产x件产品，由题意，得解不等式组，得根据题意，x的值应是整数，所以x=16.答：每个小组原先每天生产16件产品.列一元一次不等式组解实际问题的一般步骤：（1）审题；（2）设未知数，找不等量关系；（3）根据不等关系列不等式组；（4）解不等式组；（5）检验并作答.总结归纳 1.解下列不等式组： 解:（1） 1＜x＜5； （2）－4＜x≤1； （4） 无解. 当堂练习2.把一篮苹果分给几个学生，若每人分4个，则剩余
3个；若每人分6个，则最后一个学生最多分2个，
求学生人数和苹果分别是多少？解：设学生有x个,则苹果有(4x+3)个,根据题意,得解不等式组，得3.5