17.2勾股定理的逆定理优秀 课件
图片预览






文档简介
课件19张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
勾股定理的逆定理
在三角形中,若两边的平方和等于第三边的平方,
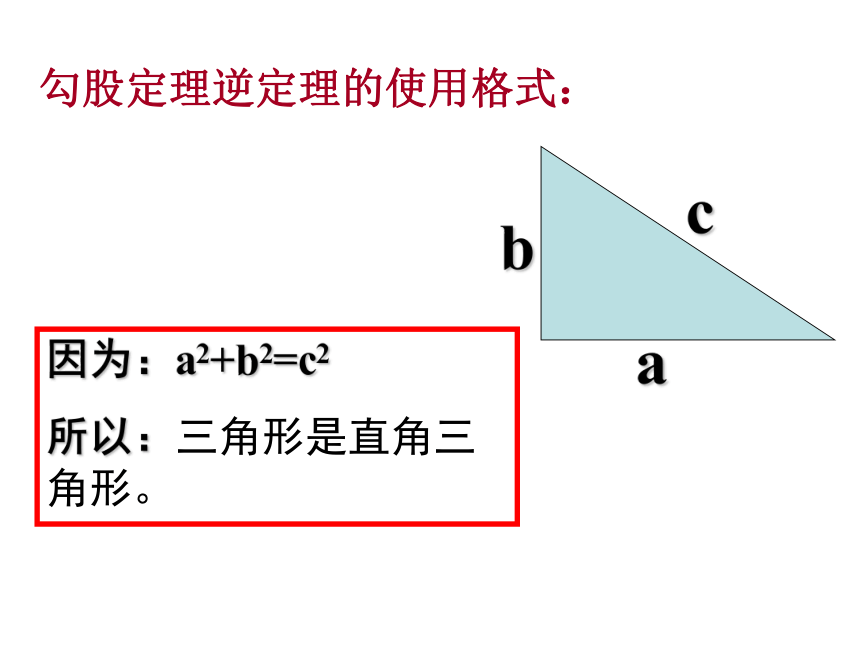
则这个三角形是直角三角形,勾股定理逆定理的使用格式:因为:a2+b2=c2
所以:三角形是直角三角形。3.下列各组线段中能够成直角三角形的是( )
A、9、41、42 B、
C、 D、4、5、61.以下各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2 ,a+1
C.a-1, ,a+1 D.a-1,a,a+1B分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形例题2如果△ABC的三边分别为a、b、c且满足 a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 这个三角形是直角三角形. 【解】由于
所以△ABC是以∠C为直角的三角形.于是
AB·CD= BC·AC,
例题3:如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90度
求:绿地ABCD的面积。CBAD242015725 一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?ABDC3451213思考题 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?某港口位于东西方向的海岸线上,ENRQSP解:根据题意画图,如图所示:PQ=16×1.5=24
PR=12×1.5=18
QR=30∵242+182=302,
即 PQ2+PR2=QR2∴∠QPR=900 由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.或东南方向③应用勾股定理(或勾股逆定理)研究解决问题的关键
是发现图中存在的直角三角形或通过添加辅助线,
在图中构造出直角三角形,有时借助方程、方程组
和代数运算;有些代数问题,其数量关系具有
“勾股关系”,根据这种关系设计、构造出相应的
几何图形,然后借助图形的几何性质去解决代数问题,
这就是“数形结合”的思想 注意:
满足 的三个正整数,称为勾股数.勾股数扩大
相同倍数后,仍为勾股数.
勾股定理的逆定理作为判断一个三角形是否是
直角三角形的依据之一,
其运用步骤为:
①确定最大边如图,在△ABC中,三边的长分别是AB=13cm,AC=12cm,BC=5cm,CD ⊥ AB于D,那么△ABC是什么形状的三角形,并求出CD的长.?练一练:证明:∵AB=13,AC=12,BC=5,
AC2+BC2=122+52=144+25=169=132=AB2,
∴ △ABC是直角三角形,且∠ ACB=90°,
AC ⊥ BC.
又∵S△ABC=1/2AC×BC=1/2×12×5=30,
∵CD ⊥ AB, S△ABC=1/2AB×CD=30,
∴CD=30×2/13=60/13.
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36观察下列表格:请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
2、如图,两个村子A,B在一条河的同侧,A,B两村
到河岸的距离分别为AC=1千米,BD=3千米,CD=3千米,
现要在河岸CD上建一水厂,向A,B两村送自来水.
铺设水管的工程费用为每千米20000元,
请你在CD上选择水厂的位置,使铺设水管的费用最省,
并求出铺设水管的费用W.
——毕达哥拉斯
勾股定理的逆定理
在三角形中,若两边的平方和等于第三边的平方,
则这个三角形是直角三角形,勾股定理逆定理的使用格式:因为:a2+b2=c2
所以:三角形是直角三角形。3.下列各组线段中能够成直角三角形的是( )
A、9、41、42 B、
C、 D、4、5、61.以下各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2 ,a+1
C.a-1, ,a+1 D.a-1,a,a+1B分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形例题2如果△ABC的三边分别为a、b、c且满足 a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 这个三角形是直角三角形. 【解】由于
所以△ABC是以∠C为直角的三角形.于是
AB·CD= BC·AC,
例题3:如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90度
求:绿地ABCD的面积。CBAD242015725 一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗? 此时四边形ABCD
的面积是多少?ABDC3451213思考题 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?某港口位于东西方向的海岸线上,ENRQSP解:根据题意画图,如图所示:PQ=16×1.5=24
PR=12×1.5=18
QR=30∵242+182=302,
即 PQ2+PR2=QR2∴∠QPR=900 由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.或东南方向③应用勾股定理(或勾股逆定理)研究解决问题的关键
是发现图中存在的直角三角形或通过添加辅助线,
在图中构造出直角三角形,有时借助方程、方程组
和代数运算;有些代数问题,其数量关系具有
“勾股关系”,根据这种关系设计、构造出相应的
几何图形,然后借助图形的几何性质去解决代数问题,
这就是“数形结合”的思想 注意:
满足 的三个正整数,称为勾股数.勾股数扩大
相同倍数后,仍为勾股数.
勾股定理的逆定理作为判断一个三角形是否是
直角三角形的依据之一,
其运用步骤为:
①确定最大边如图,在△ABC中,三边的长分别是AB=13cm,AC=12cm,BC=5cm,CD ⊥ AB于D,那么△ABC是什么形状的三角形,并求出CD的长.?练一练:证明:∵AB=13,AC=12,BC=5,
AC2+BC2=122+52=144+25=169=132=AB2,
∴ △ABC是直角三角形,且∠ ACB=90°,
AC ⊥ BC.
又∵S△ABC=1/2AC×BC=1/2×12×5=30,
∵CD ⊥ AB, S△ABC=1/2AB×CD=30,
∴CD=30×2/13=60/13.
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36观察下列表格:请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
2、如图,两个村子A,B在一条河的同侧,A,B两村
到河岸的距离分别为AC=1千米,BD=3千米,CD=3千米,
现要在河岸CD上建一水厂,向A,B两村送自来水.
铺设水管的工程费用为每千米20000元,
请你在CD上选择水厂的位置,使铺设水管的费用最省,
并求出铺设水管的费用W.
