第3章投影与视图单元检测题
图片预览

文档简介
湘教版九年级下册数学第三章投影与视图单元检测试题
一、选择题(本大题共10小题)
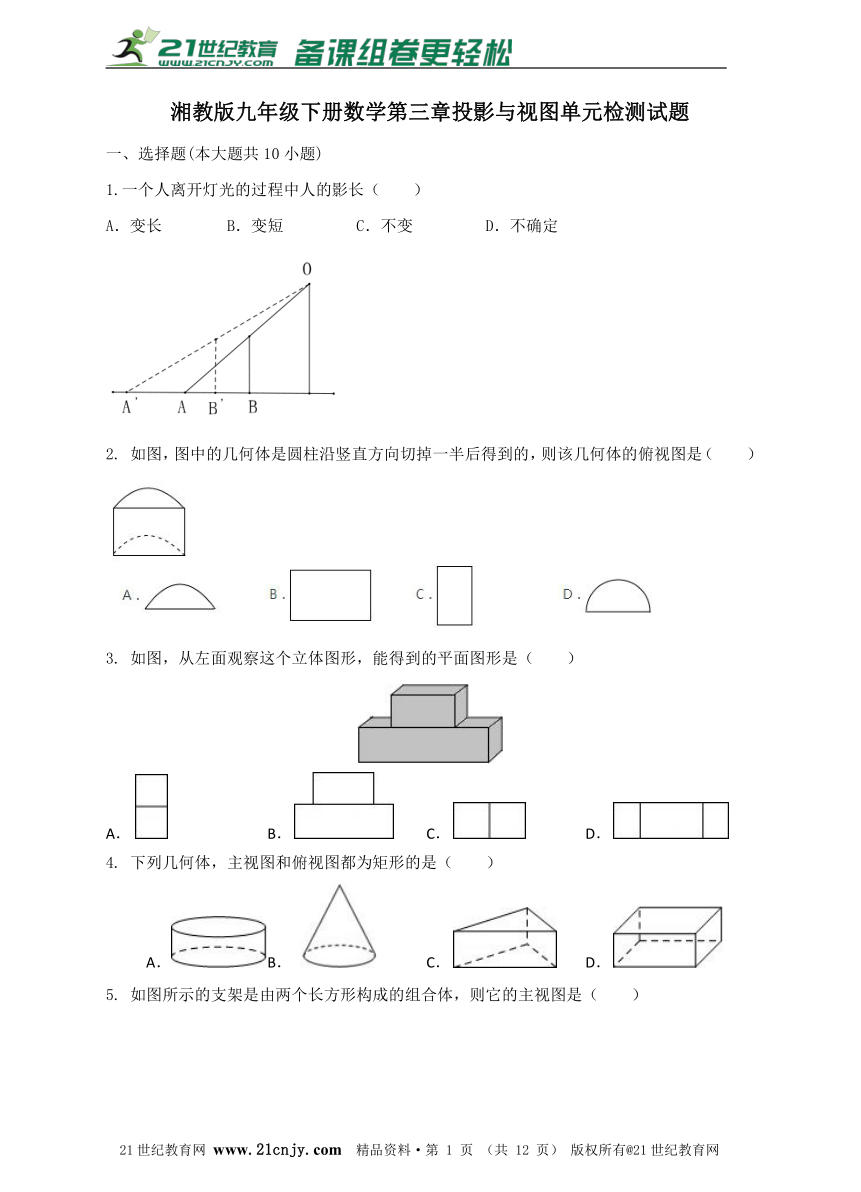
1.一个人离开灯光的过程中人的影长( )
A.变长 B.变短 C.不变 D.不确定
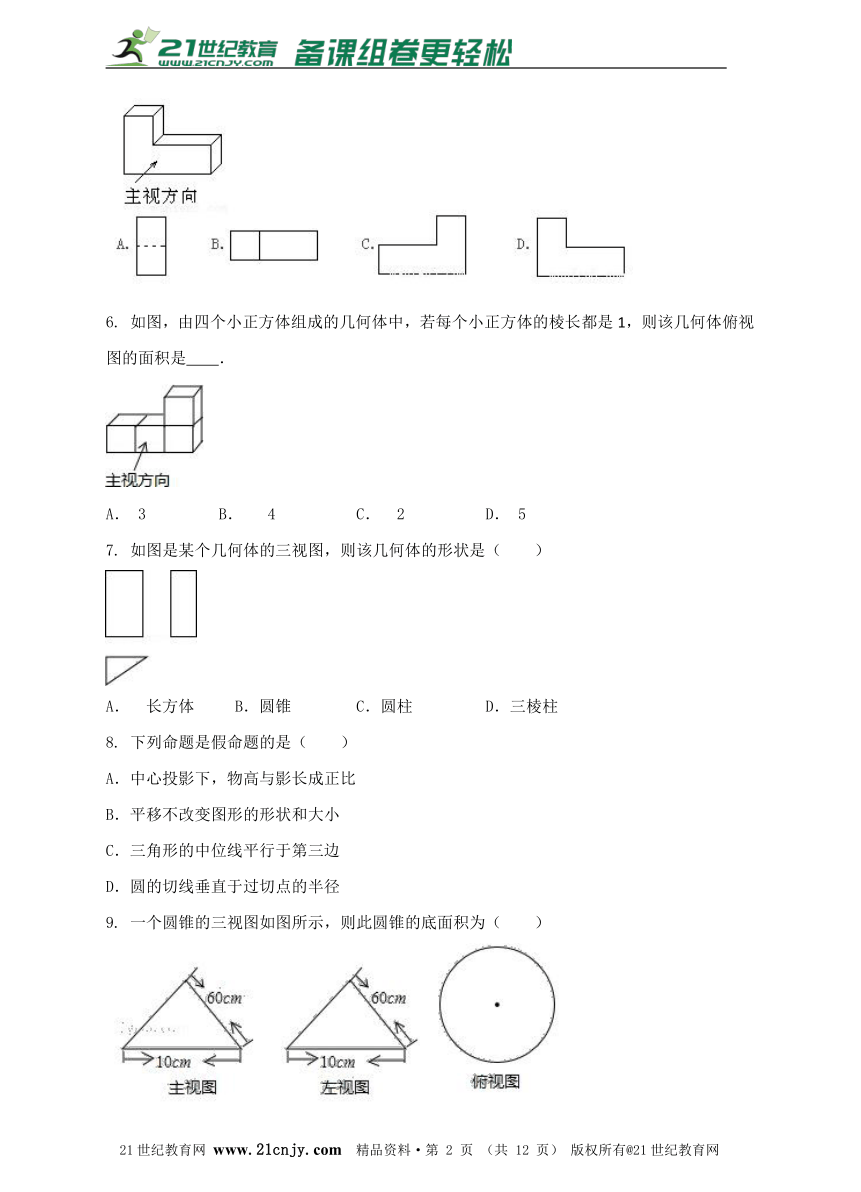
2. 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
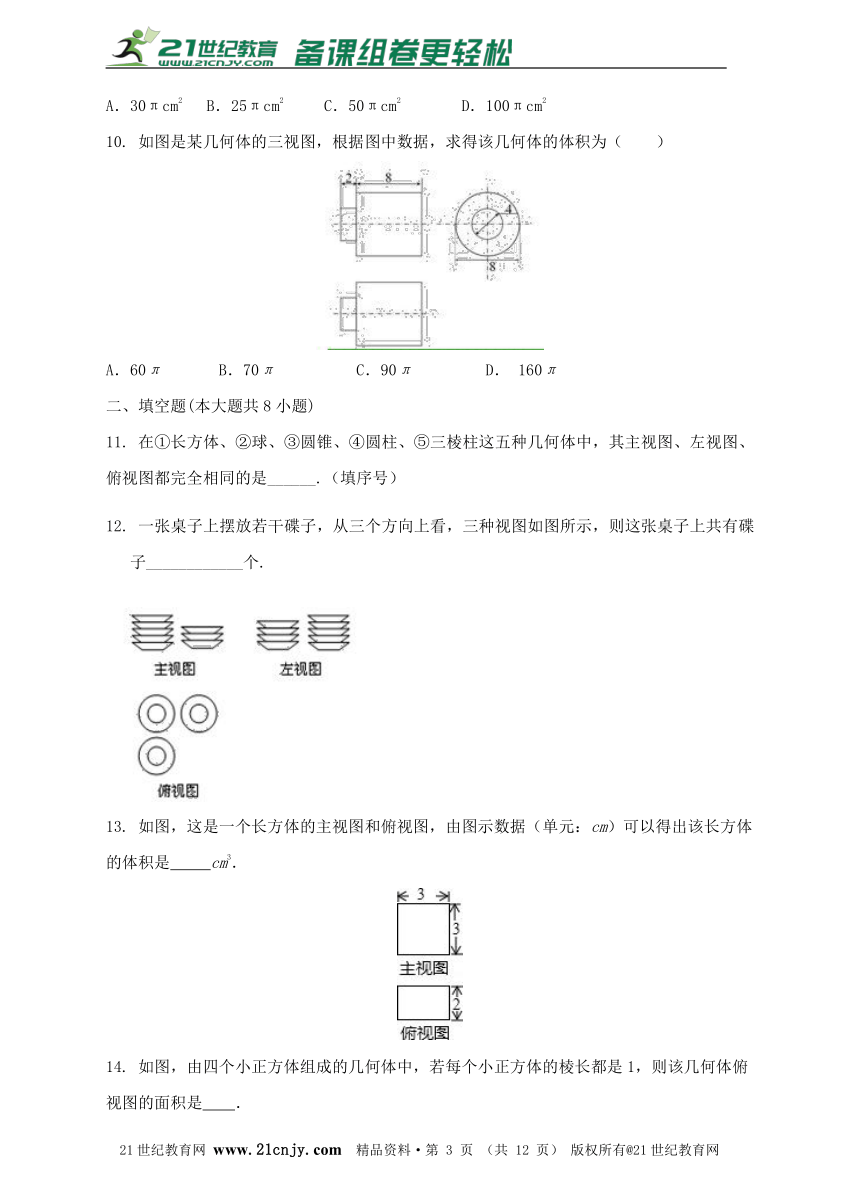
3. 如图,从左面观察这个立体图形,能得到的平面图形是( )
A. B. C. D.
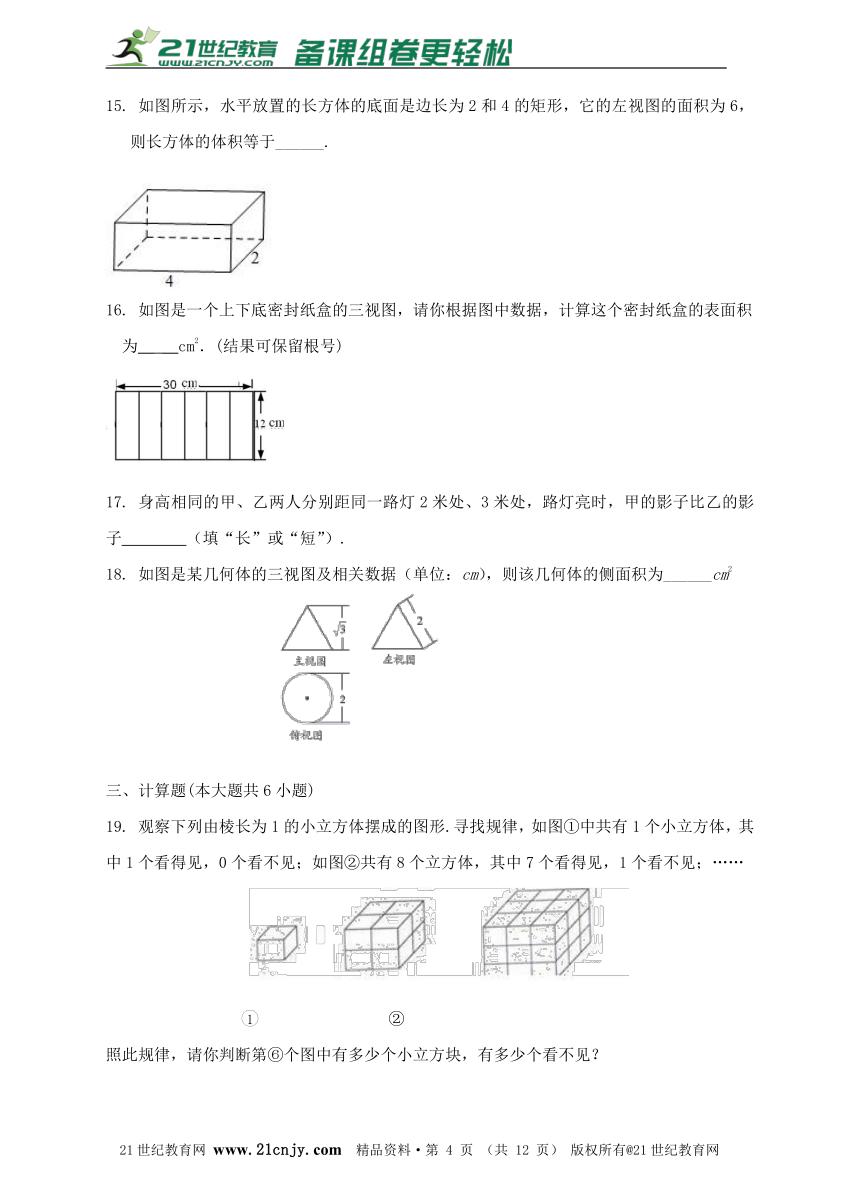
4. 下列几何体,主视图和俯视图都为矩形的是( )
A. B. C. D.
5. 如图所示的支架是由两个长方形构成的组合体,则它的主视图是( )
6. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .21世纪教育网版权所有
A. 3 B. 4 C. 2 D. 5
7. 如图是某个几何体的三视图,则该几何体的形状是( )
A. 长方体 B.圆锥 C.圆柱 D.三棱柱
8. 下列命题是假命题的是( )
A.中心投影下,物高与影长成正比
B.平移不改变图形的形状和大小
C.三角形的中位线平行于第三边
D.圆的切线垂直于过切点的半径
9. 一个圆锥的三视图如图所示,则此圆锥的底面积为( )
A.30πcm2 B.25πcm2 C.50πcm2 D.100πcm221·世纪*教育网
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D. 160π
二、填空题(本大题共8小题)
11. 在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是______.(填序号) www-2-1-cnjy-com
12. 一张桌子上摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有碟子____________个.2-1-c-n-j-y
13. 如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是 cm3.21*cnjy*com
14. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
15. 如图所示,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于______.
16. 如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为__ __cm2.(结果可保留根号)
17. 身高相同的甲、乙两人分别距同一路灯2米处、3米处,路灯亮时,甲的影子比乙的影子 (填“长”或“短”).
18. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为______cm2
三、计算题(本大题共6小题)
19. 观察下列由棱长为1的小立方体摆成的图形.寻找规律,如图①中共有1个小立方体,其中1个看得见,0个看不见;如图②共有8个立方体,其中7个看得见,1个看不见;……
②
照此规律,请你判断第⑥个图中有多少个小立方块,有多少个看不见?
20. 一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
21.圆形餐桌正上方有一个灯泡A,灯泡A照射到餐桌后在地面上形成阴影.已知餐桌的半径为0.4m、高为1m,灯泡距地面2.5m. 求地面上阴影部分的面积.
22. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一段高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是投影的有关知识进行计算的.
(2)试计算出电线杆的高度,并写出计算的过程.
23. 如图,花丛中有一路灯杆AB,在灯光下,小丽在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小丽的影长GH=5米.如果小丽的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
24. 如图所示为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4 cm,
求这个几何体的侧面积.
参考答案:
一、选择题(本大题共10小题)
1.A
分析:解答本题的关键是熟知中心投影的特点和规律,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.www.21-cn-jy.com
解:一个人从灯光下走过,光先是垂直于人的,此时人的影子最短,在人离灯越来越远时,影子就会越来越来,如图示AB为影子,A'B'为随人走离灯的影子,可知人的影子越来越大.故选A.【来源:21·世纪·教育·网】
2. D
分析: 俯视图是从物体上面看所得到的图形.
解:从几何体的上面看俯视图是,故选:D.
3. A
分析: 根据从左面看得到的图形是左视图,可得答案.
解:从左面看下面一个正方形,上面一个正方形,故选:A.
4. D
分析:根据从立体图形的三视图可得答案.
解:根据主视图和俯视图的概念可知:主视图和俯视图都为矩形的是长方体,
故选:D
5. D
分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
解:从几何体的正面看可得此几何体的主视图是,
故选:D.
6.A
分析:根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,
故答案为:3.故选A。
7. D
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
故选D.
8. A
分析:分别利用中心投影的性质以及切线的性质、平移的性质、三角形中位线定理等进行判断即可得出答案.
解:A.中心投影下,物高与影长取决于物体距光源的距离,故此选项错误,符合题意;
B.平移不改变图形的形状和大小,根据平移的性质,故此选项正确,不符合题意;
C.三角形的中位线平行于第三边,根据三角形中位线的性质,故此选项正确,不符合题意;
D.圆的切线垂直于过切点的半径,利用切线的判定定理,故此选项正确,不符合题意.
故选:A.
9. B
解析:根据主视图与左视图可以得到:圆锥的底面直径是10cm,利用圆的面积公式即可求解.
答案:解:根据主视图与左视图可以得到:圆锥的底面直径是10cm,则此圆锥的底面积为:π()2=25πcm2.故选B.21·cn·jy·com
10. B
分析:易得此几何体为空心圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解.
解:观察三视图发现该几何体为空心圆柱,其内径为3,外径为4,高为10,
所以其体积为10×(42π﹣32π)=70π,
故选B.
二、填空题(本大题共8小题)
11.分析:具体分析五种立体图形的三视图来判断即可。
解:长方体的三视图都是矩形,但是矩形的大小不一样,所以①不符合;
球的三视图都是相同大小的圆,所以②符合;
圆锥的主视图和左视图都是三角形,而俯视图是中心带圆点的圆,所以③不符合;
圆柱的主视图和左视图都是矩形,而俯视图是圆,所以④不符合;
三棱柱主视图和左视图是矩形,俯视图是三角形,所以⑤也不符合.
12. 分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解:从三视图看,第一列有4+5=9(个),第二列有3个,
则这个桌子上共有9+3=12(个)碟子.故答案为12.
13.分析:首先确定该几何体为立方体,并说出其尺寸,直接计算其体积即可.
解:观察其视图知:该几何体为立方体,且立方体的长为3,宽为2,高为3,
故其体积为:3×3×2=18,故答案为:18.
14. 分析: 根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,
故答案为:3.
点评:本题考查了简单组合体的三视图,先确定俯视图,再求面积.
15. 分析:长方体的左视图是一个矩形,因为它的面积为6,一边长为2,所以另一边长为3,从而得出长方体的高为3,因此长方体的体积等于2×4×3=24.21cnjy.com
解:长方体的左视图是一个矩形,
因为它的面积为6,一边长为2,
所以另一边长为3,从而得出长方体的高为3,
因此长方体的体积等于2×4×3=24.
16. 分析:解决三视图问题时,应熟悉常见的几何体的三视图;计算正六棱柱的表面积时注意2个底面加上侧面积。21*cnjy*com
解:据图形得,纸盒的底面为正六边形,正六边形的直径为10 cm,盒子的高为12 cm。
每个底面正六边形的面积== cm2;
侧面展开为长方形,侧面积为 cm2
所以这个密封纸盒的表面积=2个底的面积+侧面积=+360=(75+360)cm2.
17. 分析:根据中心投影的特点可得甲、乙等高,距光源距离不等,离点光源近的物体它的影子短,即可得出答案.【来源:21cnj*y.co*m】
解:中心投影的特点是:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以甲的影子比乙的影子短.【出处:21教育名师】
18. 分析:本题考查了由三视图得到几何体,然后再利用圆锥体侧面积公式求解。
解:由三视图可知,此几何体是圆锥体,母线长为2,底面直径为2,则侧面积S=lr=×2π×2=2π,故答案2π【版权所有:21教育】
三、计算题(本大题共6小题)
19. 分析:观察下列由棱长为1的小立方体摆成的图形,寻找规律:
解:照此规律,第⑥个图形中有216个小立方块,有125个小立方块看不见.
20. 分析:由已知三视图可以确定为四棱柱,首先得到棱柱底面菱形的对角线长,则求出菱形的边长,从而求出它的侧面积和体积.解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm. ∴菱形的边长为cm, 棱柱的侧面积=×4×8=80(cm2). 棱柱的体积=×3×4×8=48(cm3)21教育网
21.分析:将实际情景转化为基本图形利用相似来解答即可。
解:如图所示,设底面半径为x m,
由DE∥BC 可得 , 解得 .
∴底面面积为
22. 分析:(1)这是利用了平行投影的有关知识; (2)过点E作EM⊥AB于M,过点G作GN⊥CD于N.利用矩形的性质和平行投影的知识可以得到比例式:21教育名师原创作品
,即,由此求得CD即电线杆的高度即可.
分析:(1)这个投影的光线是太阳光,太阳光可以看成是平行光线,所以这个投影是平行投影.(2)根据平行投影中物高与影长成比例,列出比例式,由比例的性质求解.
解:(1)平行.
(2)如图,过点E作EM⊥AB于M,过点G作GN⊥CD于N,
则MB=EF=2,ND=GH=3,
ME=BF=10,NG=DH=5.所以AM=10-2=8.
由平行投影可知,即=,
解得CD=7,即电线杆的高度为7米.
23. 解:如图所示,设路灯杆AB的高度为x m.
∵CD∥AB,
∴
∴ ①
同理 ②
由①②得, ∴.
∴.
解得x≈6. 0(m).
24. 分析:(1)根据主视图和左视图是长方形,俯视图是正三角形,可得到此几何体为三棱柱;(2)应该会出现三个长方形,两个三角形;(3)侧面为3个长方形,它的长和宽分别为10,4,计算出一个长方形的面积,乘3即可.2·1·c·n·j·y
解:(1)正三棱柱;(2)如图所示;
(3)3×10×4=120().
一、选择题(本大题共10小题)
1.一个人离开灯光的过程中人的影长( )
A.变长 B.变短 C.不变 D.不确定
2. 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
3. 如图,从左面观察这个立体图形,能得到的平面图形是( )
A. B. C. D.
4. 下列几何体,主视图和俯视图都为矩形的是( )
A. B. C. D.
5. 如图所示的支架是由两个长方形构成的组合体,则它的主视图是( )
6. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .21世纪教育网版权所有
A. 3 B. 4 C. 2 D. 5
7. 如图是某个几何体的三视图,则该几何体的形状是( )
A. 长方体 B.圆锥 C.圆柱 D.三棱柱
8. 下列命题是假命题的是( )
A.中心投影下,物高与影长成正比
B.平移不改变图形的形状和大小
C.三角形的中位线平行于第三边
D.圆的切线垂直于过切点的半径
9. 一个圆锥的三视图如图所示,则此圆锥的底面积为( )
A.30πcm2 B.25πcm2 C.50πcm2 D.100πcm221·世纪*教育网
10. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D. 160π
二、填空题(本大题共8小题)
11. 在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是______.(填序号) www-2-1-cnjy-com
12. 一张桌子上摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有碟子____________个.2-1-c-n-j-y
13. 如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是 cm3.21*cnjy*com
14. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
15. 如图所示,水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于______.
16. 如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为__ __cm2.(结果可保留根号)
17. 身高相同的甲、乙两人分别距同一路灯2米处、3米处,路灯亮时,甲的影子比乙的影子 (填“长”或“短”).
18. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为______cm2
三、计算题(本大题共6小题)
19. 观察下列由棱长为1的小立方体摆成的图形.寻找规律,如图①中共有1个小立方体,其中1个看得见,0个看不见;如图②共有8个立方体,其中7个看得见,1个看不见;……
②
照此规律,请你判断第⑥个图中有多少个小立方块,有多少个看不见?
20. 一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
21.圆形餐桌正上方有一个灯泡A,灯泡A照射到餐桌后在地面上形成阴影.已知餐桌的半径为0.4m、高为1m,灯泡距地面2.5m. 求地面上阴影部分的面积.
22. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一段高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是投影的有关知识进行计算的.
(2)试计算出电线杆的高度,并写出计算的过程.
23. 如图,花丛中有一路灯杆AB,在灯光下,小丽在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小丽的影长GH=5米.如果小丽的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
24. 如图所示为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图;
(3)若长方形的高为10 cm,正三角形的边长为4 cm,
求这个几何体的侧面积.
参考答案:
一、选择题(本大题共10小题)
1.A
分析:解答本题的关键是熟知中心投影的特点和规律,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.www.21-cn-jy.com
解:一个人从灯光下走过,光先是垂直于人的,此时人的影子最短,在人离灯越来越远时,影子就会越来越来,如图示AB为影子,A'B'为随人走离灯的影子,可知人的影子越来越大.故选A.【来源:21·世纪·教育·网】
2. D
分析: 俯视图是从物体上面看所得到的图形.
解:从几何体的上面看俯视图是,故选:D.
3. A
分析: 根据从左面看得到的图形是左视图,可得答案.
解:从左面看下面一个正方形,上面一个正方形,故选:A.
4. D
分析:根据从立体图形的三视图可得答案.
解:根据主视图和俯视图的概念可知:主视图和俯视图都为矩形的是长方体,
故选:D
5. D
分析:找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
解:从几何体的正面看可得此几何体的主视图是,
故选:D.
6.A
分析:根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,
故答案为:3.故选A。
7. D
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
故选D.
8. A
分析:分别利用中心投影的性质以及切线的性质、平移的性质、三角形中位线定理等进行判断即可得出答案.
解:A.中心投影下,物高与影长取决于物体距光源的距离,故此选项错误,符合题意;
B.平移不改变图形的形状和大小,根据平移的性质,故此选项正确,不符合题意;
C.三角形的中位线平行于第三边,根据三角形中位线的性质,故此选项正确,不符合题意;
D.圆的切线垂直于过切点的半径,利用切线的判定定理,故此选项正确,不符合题意.
故选:A.
9. B
解析:根据主视图与左视图可以得到:圆锥的底面直径是10cm,利用圆的面积公式即可求解.
答案:解:根据主视图与左视图可以得到:圆锥的底面直径是10cm,则此圆锥的底面积为:π()2=25πcm2.故选B.21·cn·jy·com
10. B
分析:易得此几何体为空心圆柱,圆柱的体积=底面积×高,把相关数值代入即可求解.
解:观察三视图发现该几何体为空心圆柱,其内径为3,外径为4,高为10,
所以其体积为10×(42π﹣32π)=70π,
故选B.
二、填空题(本大题共8小题)
11.分析:具体分析五种立体图形的三视图来判断即可。
解:长方体的三视图都是矩形,但是矩形的大小不一样,所以①不符合;
球的三视图都是相同大小的圆,所以②符合;
圆锥的主视图和左视图都是三角形,而俯视图是中心带圆点的圆,所以③不符合;
圆柱的主视图和左视图都是矩形,而俯视图是圆,所以④不符合;
三棱柱主视图和左视图是矩形,俯视图是三角形,所以⑤也不符合.
12. 分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解:从三视图看,第一列有4+5=9(个),第二列有3个,
则这个桌子上共有9+3=12(个)碟子.故答案为12.
13.分析:首先确定该几何体为立方体,并说出其尺寸,直接计算其体积即可.
解:观察其视图知:该几何体为立方体,且立方体的长为3,宽为2,高为3,
故其体积为:3×3×2=18,故答案为:18.
14. 分析: 根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,
故答案为:3.
点评:本题考查了简单组合体的三视图,先确定俯视图,再求面积.
15. 分析:长方体的左视图是一个矩形,因为它的面积为6,一边长为2,所以另一边长为3,从而得出长方体的高为3,因此长方体的体积等于2×4×3=24.21cnjy.com
解:长方体的左视图是一个矩形,
因为它的面积为6,一边长为2,
所以另一边长为3,从而得出长方体的高为3,
因此长方体的体积等于2×4×3=24.
16. 分析:解决三视图问题时,应熟悉常见的几何体的三视图;计算正六棱柱的表面积时注意2个底面加上侧面积。21*cnjy*com
解:据图形得,纸盒的底面为正六边形,正六边形的直径为10 cm,盒子的高为12 cm。
每个底面正六边形的面积== cm2;
侧面展开为长方形,侧面积为 cm2
所以这个密封纸盒的表面积=2个底的面积+侧面积=+360=(75+360)cm2.
17. 分析:根据中心投影的特点可得甲、乙等高,距光源距离不等,离点光源近的物体它的影子短,即可得出答案.【来源:21cnj*y.co*m】
解:中心投影的特点是:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以甲的影子比乙的影子短.【出处:21教育名师】
18. 分析:本题考查了由三视图得到几何体,然后再利用圆锥体侧面积公式求解。
解:由三视图可知,此几何体是圆锥体,母线长为2,底面直径为2,则侧面积S=lr=×2π×2=2π,故答案2π【版权所有:21教育】
三、计算题(本大题共6小题)
19. 分析:观察下列由棱长为1的小立方体摆成的图形,寻找规律:
解:照此规律,第⑥个图形中有216个小立方块,有125个小立方块看不见.
20. 分析:由已知三视图可以确定为四棱柱,首先得到棱柱底面菱形的对角线长,则求出菱形的边长,从而求出它的侧面积和体积.解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm. ∴菱形的边长为cm, 棱柱的侧面积=×4×8=80(cm2). 棱柱的体积=×3×4×8=48(cm3)21教育网
21.分析:将实际情景转化为基本图形利用相似来解答即可。
解:如图所示,设底面半径为x m,
由DE∥BC 可得 , 解得 .
∴底面面积为
22. 分析:(1)这是利用了平行投影的有关知识; (2)过点E作EM⊥AB于M,过点G作GN⊥CD于N.利用矩形的性质和平行投影的知识可以得到比例式:21教育名师原创作品
,即,由此求得CD即电线杆的高度即可.
分析:(1)这个投影的光线是太阳光,太阳光可以看成是平行光线,所以这个投影是平行投影.(2)根据平行投影中物高与影长成比例,列出比例式,由比例的性质求解.
解:(1)平行.
(2)如图,过点E作EM⊥AB于M,过点G作GN⊥CD于N,
则MB=EF=2,ND=GH=3,
ME=BF=10,NG=DH=5.所以AM=10-2=8.
由平行投影可知,即=,
解得CD=7,即电线杆的高度为7米.
23. 解:如图所示,设路灯杆AB的高度为x m.
∵CD∥AB,
∴
∴ ①
同理 ②
由①②得, ∴.
∴.
解得x≈6. 0(m).
24. 分析:(1)根据主视图和左视图是长方形,俯视图是正三角形,可得到此几何体为三棱柱;(2)应该会出现三个长方形,两个三角形;(3)侧面为3个长方形,它的长和宽分别为10,4,计算出一个长方形的面积,乘3即可.2·1·c·n·j·y
解:(1)正三棱柱;(2)如图所示;
(3)3×10×4=120().
