福建省漳州市龙海市程溪中学2016-2017学年高二(上)期末数学试卷(理科)(解析版)
文档属性
| 名称 | 福建省漳州市龙海市程溪中学2016-2017学年高二(上)期末数学试卷(理科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 385.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 15:29:31 | ||
图片预览



文档简介
2016-2017学年福建省漳州市龙海市程溪中学高二(上)期末数学试卷(理科)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题:“ x>0,x2﹣x≥0”的否定形式是( )
A. x≤0,x2﹣x>0
B. x>0,x2﹣x≤0
C. x≤0,x2﹣x>0
D. x>0,x2﹣x<0
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,若用系统抽样方法,则所抽取的编号可能是( )
A.2,4,6,8
B.2,6,10,14
C.2,7,12,17
D.5,8,9,14
3.曲线y=与直线y=x﹣1及x=4所围成的封闭图形的面积为( )
A.2ln
2
B.2﹣ln
2
C.4﹣ln
2
D.4﹣2ln
2
4.抛物线y=4x2的焦点坐标是( )
A.(0,1)
B.(1,0)
C.
D.
5.函数f(x)=x2﹣2lnx的单调减区间是( )
A.(0,1)
B.(1,+∞)
C.(﹣∞,﹣1)∪(0,1)
D.(﹣1,0)∪(0,1)
6.在空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,N为BC的中点,则等于( )
A.
﹣+
B.﹣++
C.
D.
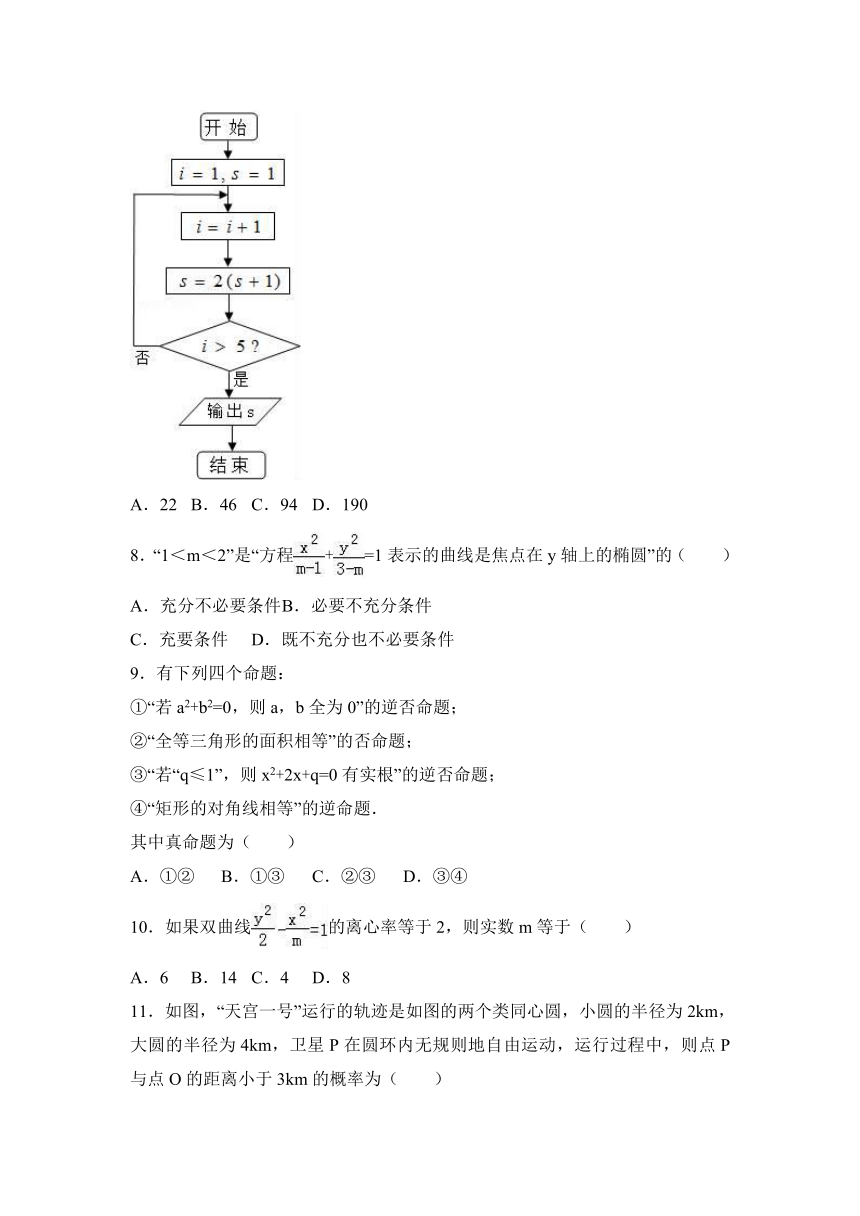
7.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
8.“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
9.有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
A.①②
B.①③
C.②③
D.③④
10.如果双曲线的离心率等于2,则实数m等于( )
A.6
B.14
C.4
D.8
11.如图,“天宫一号”运行的轨迹是如图
( http: / / www.21cnjy.com )的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
A.
B.
C.
D.
12.已知函数y=f(x)对任意的x∈(﹣
( http: / / www.21cnjy.com ),)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.
f(﹣)<f(﹣)
B.
f()<f()
C.f(0)>2f()
D.f(0)>f()
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.
13.由定积分的几何意义可知dx= .
14.已知p:(x+2)(x﹣3)≤0,q:|x+1|≥2,命题“p∧q”为真,则实数x的取值范围是 .
15.椭圆+y2=1中,以点M(1,)为中点的弦所在直线方程是 .
16.已知方程﹣=0有两个不等的非零根,则a的取值范围是 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
18.已知函数f(x)=2x3+3x2﹣12x+5.
(Ⅰ)求曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)求函数f(x)的极值.
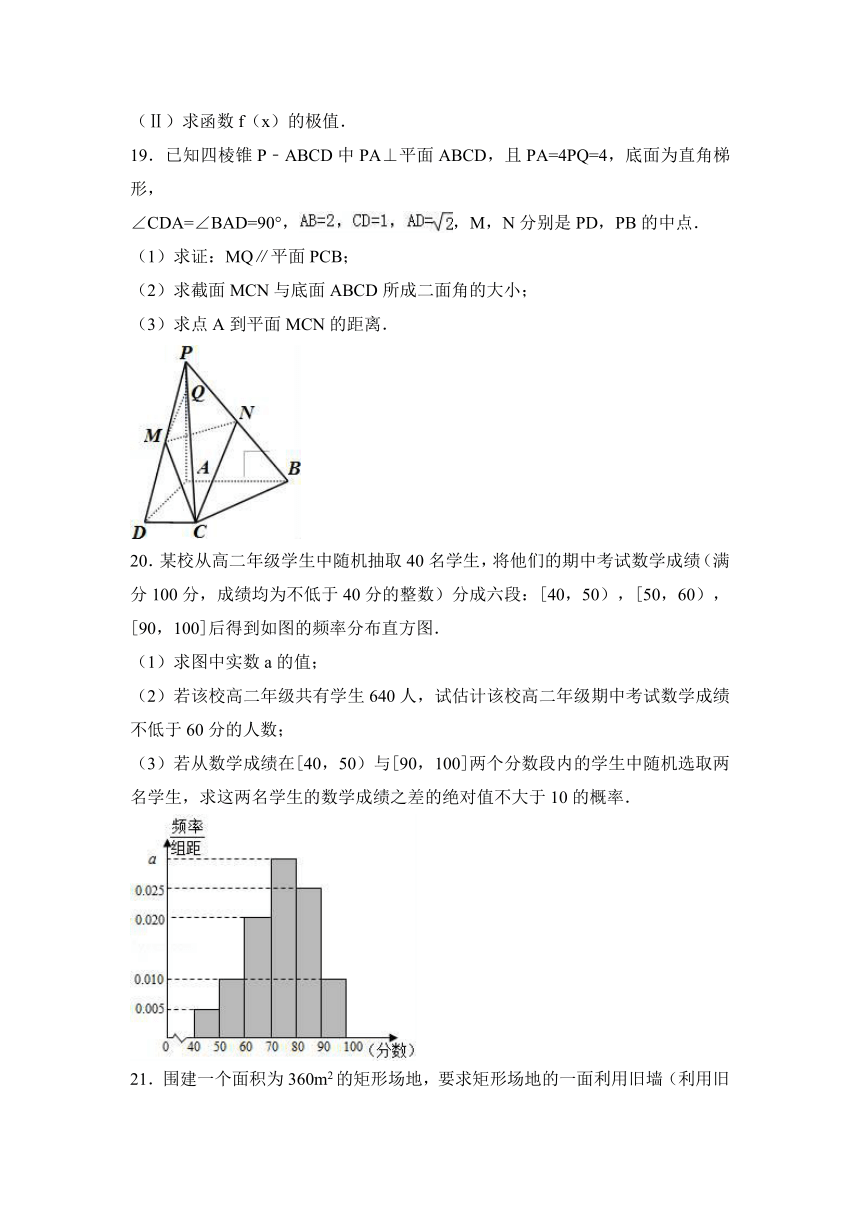
19.已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,
∠CDA=∠BAD=90°,,M,N分别是PD,PB的中点.
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
20.某校从高二年级学生中随机抽取40名学
( http: / / www.21cnjy.com )生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40
( http: / / www.21cnjy.com ),50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
21.围建一个面积为360m2的矩形场
( http: / / www.21cnjy.com )地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
22.已知椭圆C:
=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点
M,N.
(1)求椭圆C的方程,并求其焦点坐标;
(2)当△AMN的面积为时,求k的值.
2016-2017学年福建省漳州市龙海市程溪中学高二(上)期末数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题:“ x>0,x2﹣x≥0”的否定形式是( )
A. x≤0,x2﹣x>0
B. x>0,x2﹣x≤0
C. x≤0,x2﹣x>0
D. x>0,x2﹣x<0
【考点】命题的否定.
【分析】通常像“所有”、“任意”、
( http: / / www.21cnjy.com )“每一个”等表示全体的量词在逻辑中称为全称量词,通常用符号“ x”表示“对任意x”;“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为存在量词,通常用符号“ x”表示“存在x”.
【解答】解:命题p: x∈R,x2﹣x≥0的否定形式是特称命题;
“ x∈R,x2﹣x<0”.
故选:D
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,若用系统抽样方法,则所抽取的编号可能是( )
A.2,4,6,8
B.2,6,10,14
C.2,7,12,17
D.5,8,9,14
【考点】系统抽样方法.
【分析】根据系统抽样的定义确定样本数据的组距即可得到结论.
【解答】解:从20位同学,编号从1至20,现在从中抽取4人作问卷调查,则组距为20÷4=5,
则4个号码差距为5.
则满足条件的号码可能是2,7,12,17.
故选:C.
3.曲线y=与直线y=x﹣1及x=4所围成的封闭图形的面积为( )
A.2ln
2
B.2﹣ln
2
C.4﹣ln
2
D.4﹣2ln
2
【考点】定积分.
【分析】先联立两个曲线的方程,求出
( http: / / www.21cnjy.com )交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.先联立两个曲线的方程,求出交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.
【解答】解:由曲线y=与直线y=x﹣1联立,解得,x=﹣1,x=2,
故所求图形的面积为S=(x﹣1﹣)dx=(x2﹣x﹣2lnx)|=4﹣2ln2.
故选:C.
4.抛物线y=4x2的焦点坐标是( )
A.(0,1)
B.(1,0)
C.
D.
【考点】抛物线的简单性质.
【分析】把抛物线y=4x2的方程化为标准形式,确定开口方向和p值,即可得到焦点坐标.
【解答】解:抛物线y=4x2的标准方程为
x2=y,p=,开口向上,焦点在y轴的正半轴上,
故焦点坐标为(0,),
故选C.
5.函数f(x)=x2﹣2lnx的单调减区间是( )
A.(0,1)
B.(1,+∞)
C.(﹣∞,﹣1)∪(0,1)
D.(﹣1,0)∪(0,1)
【考点】利用导数研究函数的单调性.
【分析】依题意,可求得f′(x),由f′(x)<0即可求得函数f(x)=x2﹣2lnx的单调减区间.
【解答】解:∵f(x)=x2﹣2lnx(x>0),
∴f′(x)=2x﹣=,
令f′(x)<0由图得:0<x<1,
∴函数f(x)=x2﹣2lnx的单调减区间是(0,1),
故选:A.
6.在空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,N为BC的中点,则等于( )
A.
﹣+
B.﹣++
C.
D.
【考点】向量加减混合运算及其几何意义.
【分析】由题意结合图形,直接利用,求出,然后即可解答.
【解答】解:因为空间四边形OABC如图,,,,
点M在线段OA上,且OM=2MA,N为BC的中点,
所以=.
所以=.
故选B.
7.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
【考点】循环结构;设计程序框图解决实际问题.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S值.
【解答】解:程序运行过程中,各变量的值如下表示:
i
S
是否继续循环
循环前
1
1/
第一圈
2
4
是
第二圈
3
10
是
第三圈
4
22
是
第四圈
5
46
是
第五圈
6
94
否
故输入的S值为94
故选C.
8.“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据椭圆的性质,结合充分条件和必要条件的定义进行判断即可.
【解答】解:若方程+=1表示的曲线是焦点在y轴上的椭圆,
则,
即,
解得1<m<2,即“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的充要条件,
故选:C
9.有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
A.①②
B.①③
C.②③
D.③④
【考点】命题的真假判断与应用.
【分析】①由于“若a2+b2=0,则a,b全为0”是真命题,由于逆否命题与原命题是等价命题,即可判断出;
②“全等三角形的面积相等”的否命题为“不全等的三角形的面积不相等”,是假命题;
③若x2+2x+q=0有实根,则△=4﹣4q≥0,解得q≤1,即可判断出;
④“矩形的对角线相等”的逆命题为“对角线相等的四边形是矩形”,即可判断出.
【解答】解:①由于“若a2+b2=0,则a,b全为0”是真命题,因此其逆否命题是真命题;
②“全等三角形的面积相等”的否命题为“不全等的三角形的面积不相等”,不正确;
③若x2+2x+q=0有实根,则△=4﹣4q≥0,解得q≤1,因此“若“q≤1”,则x2+2x+q=0有实根”的逆否命题是真命题;
④“矩形的对角线相等”的逆命题为“对角线相等的四边形是矩形”,是假命题.
综上可得:真命题为:①③.
故选:B.
10.如果双曲线的离心率等于2,则实数m等于( )
A.6
B.14
C.4
D.8
【考点】双曲线的简单性质.
【分析】直接求出双曲线的实轴长,焦距的长,然后利用双曲线的离心率,求出m值.
【解答】解:因为双曲线为,所以2a=2,b=,
所以c=,因为双曲线的离心率等于2,
所以2=,所以m=6.
故选A.
11.如图,“天宫一号”运行的轨迹是如图的两
( http: / / www.21cnjy.com )个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
A.
B.
C.
D.
【考点】几何概型.
【分析】点P与点O的距离小
( http: / / www.21cnjy.com )于3cm,也就是说以O点为圆心,3CM为半径作一个圆,这个圆的面积减去小圆的面积就是点P与点O的距离小于3cm的机会(一个圆环的面积),而P可能落在的面积为大圆面积减小圆面积,也就是整个圆环的面积,点P与点O距离小于3cm的概率=小圆环的面积:大圆环的面积.
【解答】解:如图所示,
S大圆环=42π﹣22π=12π,
S小圆环=32π﹣22π=5π,
所以,点P与点O距离小于3cm的概率==.
故选B.
12.已知函数y=f(x
( http: / / www.21cnjy.com ))对任意的x∈(﹣,)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.
f(﹣)<f(﹣)
B.
f()<f()
C.f(0)>2f()
D.f(0)>f()
【考点】利用导数研究函数的单调性.
【分析】根据条件构造函数g(x)=,求函数的导数,利用函数的单调性和导数之间的关系即可得到结论.
【解答】解:构造函数g(x)=,
则g′(x)==(f′(x)cosx+f(x)sinx),
∵对任意的x∈(﹣,)满足f′(x)cosx+f(x)sinx>0,
∴g′(x)>0,即函数g(x)在x∈(﹣,)单调递增,
则g(﹣)<g(﹣),即,
∴,即f(﹣)<f(﹣),故A正确.
g(0)<g(),即,
∴f(0)<2f(),
故选:A.
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.
13.由定积分的几何意义可知dx= 2π .
【考点】定积分.
【分析】本题利用定积分的几何意义计算定积分,即求被积函数y=与x轴所围成的图形的面积即可.
【解答】解:根据定积分的几何意义,则
dx表示圆心在原点,半径为2的圆的上半圆的面积,
故
dx=×π×22=2π.
故答案为:2π.
14.已知p:(x+2)(x﹣3)≤0,q:|x+1|≥2,命题“p∧q”为真,则实数x的取值范围是 [1,3] .
【考点】复合命题的真假.
【分析】分别解出p,q的x的范围,再利用命题“p∧q”为真即可得出.
【解答】解:p:(x+2)(x﹣3)≤0,解得﹣2≤x≤3.
q:|x+1|≥2,解得x≥1或x≤﹣3.
命题“p∧q”为真,∴,解得1≤x≤3.
则实数x的取值范围是[1,3].
故答案为:[1,3].
15.椭圆+y2=1中,以点M(1,)为中点的弦所在直线方程是 x+2y﹣2=0 .
【考点】椭圆的简单性质.
【分析】判断M在椭圆内,设弦AB的端点
( http: / / www.21cnjy.com )为(x1,y1),(x2,y2),代入椭圆方程,运用点差法,结合直线的斜率公式和中点坐标公式,再由点斜式方程,即可得到所求方程.
【解答】解:由M点代入椭圆方程可得,
+<1,
即M在椭圆内,则直线与椭圆相交.
设弦AB的端点为(x1,y1),(x2,y2),
即有+y12=1,
+y22=1,
两式相减可得,
+(y1﹣y2)(y1+y2)=0,
由中点坐标公式可得,x1+x2=2,y1+y2=1,
代入上式,可得kAB==﹣=﹣,
即有弦所在的直线方程为y﹣=﹣(x﹣1),
即为x+2y﹣2=0.
故答案为:x+2y﹣2=0.
16.已知方程﹣=0有两个不等的非零根,则a的取值范围是 (0,) .
【考点】根的存在性及根的个数判断.
【分析】由方程﹣=0得a=,x≠0;再令f(x)=,从而求导f′(x)=以确定函数的单调性及取值,从而确定a的取值范围.
【解答】解:由方程﹣=0得,
a=,x≠0;
令f(x)=,
则f′(x)=;
故f(x)在(﹣∞,1)上是增函数,且f(x)<f(1)=;
在(1,+∞)上是减函数,且0<f(x)<;
故若方程﹣=0有两个不等的非零根,
则a的取值范围是(0,).
故答案为:(0,).
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
【考点】回归分析的初步应用.
【分析】(1)根据表中所给的数据,做出
( http: / / www.21cnjy.com )横标和纵标的平均数,得到样本中心点,求出对应的横标和纵标的积的和,求出横标的平方和,做出系数和a的值,写出线性回归方程.
(2)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05.试预测加工10个零件需要8.05个小时,这是一个预报值.
【解答】解:(1)由表中数据得:
xiyi=52.5,
=3.5,
=3.5,
xi2=54.
∴b==0.7
故a=3.5﹣0.7×3.5=1.05,
∴所求线性回归方程为:y=0.7x+1.05.
(2)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时).
∴试预测加工10个零件需要8.05个小时.
18.已知函数f(x)=2x3+3x2﹣12x+5.
(Ⅰ)求曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)求函数f(x)的极值.
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的极值.
【分析】(Ⅰ)求出函数的导数在x=0的导数值,就是切线的斜率,利用点斜式求解曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)利用函数的导数为0,求出极值点,判断导函数的符号,即可求函数f(x)的极值.
【解答】(本小题满分12分)
解:f′(x)=6x2+6x﹣12…
(Ⅰ)依题意可知:k=f′(x)|x=0=﹣12…
∴切线方程为:y﹣5=﹣12x
即12x+y﹣5=0…
(Ⅱ)令f′(x)=0,得:x1=﹣2,x2=1…
x
(﹣∞,﹣2)
﹣2
(﹣2,1)
1
(1,+∞)
f'(x)
+
0
﹣
+
f(x)
↑
极大值25
↓
极小值﹣2
↑
…
∴f(x)的极大值为f(﹣2)=25,极小值为f(1)=﹣2…
19.已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,
∠CDA=∠BAD=90°,,M,N分别是PD,PB的中点.
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
【考点】与二面角有关的立体几何综合题;直线与平面平行的判定;点、线、面间的距离计算.
【分析】此类题一般有两种解法,一种是利用空间向量方法来证明,一种是用立体几何中线面位置关系进行证明,本题提供两种解法
向量法:对于(1)求证:MQ∥平面PCB,可求出线的方向向量与面的法向量,如果两者的内积为0则说明线面平行
对于(2)求截面MCN与底面ABCD所成二面角的大小,求出两个平面的法向量,然后根据根据二面角的正弦与法向量的数量积的关系,求解;
对于(3)求点A到平面MCN的距离
( http: / / www.21cnjy.com ),求出平面上任一点与A连线所对应的向量,求这个向量在该平面的法向量上的投影即可,此法求点到面的距离甚为巧妙.
几何法:(1)求证MQ∥平面PCB,用线面平行的判定定理证明即可;
(2)求截面MCN与底面ABCD所成二面
( http: / / www.21cnjy.com )角的大小,先在图形中作出二面角的平面角,再证明其是二面角的平面角,然后根据题设中的条件求出平面角的三角函数值,一般要在一个三角形中求解函数值.
(3)求点A到平面MCN的距离,须先作出点A在面上的垂线段,然后在三角形中求出此线段的长度即可.
【解答】解:法一向量法:
以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O﹣xyz,
由,PA=4PQ=4,M,N分别是PD,PB的中点,
可得:,
∴,
设平面的PBC的法向量为,
则有:
令z=1,则,
∴,
又MQ 平面PCB,∴MQ∥平面PCB;
(2)设平面的MCN的法向量为,又
则有:
令z=1,则,
又为平面ABCD的法向量,
∴,又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为,
(3)∵,∴所求的距离;
法二,几何法:
(1)取AP的中点E,连接ED,则ED∥CN,依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,
又MQ 平面PCB,CN 平面PCB,∴MQ∥平面PCB
(2)易证:平面MEN∥底面ABCD,所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的二面角,
因为PA⊥平面ABCD,所以PA⊥平面MEN,过E做EF⊥MN,垂足为F,连接QF,
则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面所以∠QFE为截面MCN与平面MEN所成的二面角的平面角,,
所以:,
所以:;
(3)因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,
由(2)知:MN⊥平面QEF,则平面
( http: / / www.21cnjy.com )MCNQ⊥平面QEF且交线为QF,作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.
.
20.某校从高二年级学生中随机抽取40
( http: / / www.21cnjy.com )名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,5
( http: / / www.21cnjy.com )0)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
【考点】古典概型及其概率计算公式;频率分布直方图.
【分析】(1)根据阴影矩形的面积之和等于1,计算a的值;
(2)首先计算成绩不低于60分的频率,即后四个小矩形的面积和,然后用640×频率计算人数;
(3)若两名学生的学生成绩之差的绝对值
( http: / / www.21cnjy.com )不大于10,即两人是同一组的学生,那么首先计算两组的人数,并编号,并以编号的形式列出所有选取2人的基本事件的个数,同时计算同一组的两个人的所有基本事件的个数,最后相除得到概率.
【解答】(1)解:由于图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03.
(2)解:根据频率分布直方图,成绩不低于6的频率为
1﹣10×(0.005+0.01)=0.85.
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于6的人数约为640×0.85=544人.
(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:
(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
所以所求概率为P(M)=.
21.围建一个面积为360m2的矩形场地,
( http: / / www.21cnjy.com )要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
【考点】函数模型的选择与应用;函数的值域;基本不等式在最值问题中的应用.
【分析】(I)设矩形的另一边
( http: / / www.21cnjy.com )长为am,则根据围建的矩形场地的面积为360m2,易得,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;
(II)根据(I)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值.
【解答】解:(Ⅰ)设矩形的另一边长为am,
则y=45x+180(x﹣2)+180 2a=225x+360a﹣360.
由已知ax=360,得,
所以.
(II)因为x>0,所以,
所以,当且仅当时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
22.已知椭圆C:
=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点
M,N.
(1)求椭圆C的方程,并求其焦点坐标;
(2)当△AMN的面积为时,求k的值.
【考点】椭圆的简单性质.
【分析】(1)由题意可得:a=2,,a2=b2+c2,联立解得即可得出.
(2)设M(x1,y1),N(x2,y
( http: / / www.21cnjy.com )2),直线方程与椭圆方程联立化为:(1+2k2)x2﹣4k2x+2k2﹣4=0,利用根与系数的关系可得|MN|=,点A到直线MN的距离d.利用△AMN的面积==|MN|,解出即可得出.
【解答】解:(1)由题意可得:a=2,,a2=b2+c2,联立解得a=2,c=b=.
∴椭圆C的标准方程为:
=1,其焦点坐标为:.
(2)设M(x1,y1),N(x2,y2),联立,
化为:(1+2k2)x2﹣4k2x+2k2﹣4=0,
△>0,∴x1+x2=,x1x2=.
∴|MN|=
==.
点A到直线MN的距离d=.
∴△AMN的面积==|MN|=,
化为:20k4﹣7k2﹣13=0,
解得k2=1,解得k=±1.
2017年3月8日
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题:“ x>0,x2﹣x≥0”的否定形式是( )
A. x≤0,x2﹣x>0
B. x>0,x2﹣x≤0
C. x≤0,x2﹣x>0
D. x>0,x2﹣x<0
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,若用系统抽样方法,则所抽取的编号可能是( )
A.2,4,6,8
B.2,6,10,14
C.2,7,12,17
D.5,8,9,14
3.曲线y=与直线y=x﹣1及x=4所围成的封闭图形的面积为( )
A.2ln
2
B.2﹣ln
2
C.4﹣ln
2
D.4﹣2ln
2
4.抛物线y=4x2的焦点坐标是( )
A.(0,1)
B.(1,0)
C.
D.
5.函数f(x)=x2﹣2lnx的单调减区间是( )
A.(0,1)
B.(1,+∞)
C.(﹣∞,﹣1)∪(0,1)
D.(﹣1,0)∪(0,1)
6.在空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,N为BC的中点,则等于( )
A.
﹣+
B.﹣++
C.
D.
7.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
8.“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
9.有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
A.①②
B.①③
C.②③
D.③④
10.如果双曲线的离心率等于2,则实数m等于( )
A.6
B.14
C.4
D.8
11.如图,“天宫一号”运行的轨迹是如图
( http: / / www.21cnjy.com )的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
A.
B.
C.
D.
12.已知函数y=f(x)对任意的x∈(﹣
( http: / / www.21cnjy.com ),)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.
f(﹣)<f(﹣)
B.
f()<f()
C.f(0)>2f()
D.f(0)>f()
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.
13.由定积分的几何意义可知dx= .
14.已知p:(x+2)(x﹣3)≤0,q:|x+1|≥2,命题“p∧q”为真,则实数x的取值范围是 .
15.椭圆+y2=1中,以点M(1,)为中点的弦所在直线方程是 .
16.已知方程﹣=0有两个不等的非零根,则a的取值范围是 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
18.已知函数f(x)=2x3+3x2﹣12x+5.
(Ⅰ)求曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)求函数f(x)的极值.
19.已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,
∠CDA=∠BAD=90°,,M,N分别是PD,PB的中点.
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
20.某校从高二年级学生中随机抽取40名学
( http: / / www.21cnjy.com )生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40
( http: / / www.21cnjy.com ),50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
21.围建一个面积为360m2的矩形场
( http: / / www.21cnjy.com )地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
22.已知椭圆C:
=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点
M,N.
(1)求椭圆C的方程,并求其焦点坐标;
(2)当△AMN的面积为时,求k的值.
2016-2017学年福建省漳州市龙海市程溪中学高二(上)期末数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题:“ x>0,x2﹣x≥0”的否定形式是( )
A. x≤0,x2﹣x>0
B. x>0,x2﹣x≤0
C. x≤0,x2﹣x>0
D. x>0,x2﹣x<0
【考点】命题的否定.
【分析】通常像“所有”、“任意”、
( http: / / www.21cnjy.com )“每一个”等表示全体的量词在逻辑中称为全称量词,通常用符号“ x”表示“对任意x”;“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为存在量词,通常用符号“ x”表示“存在x”.
【解答】解:命题p: x∈R,x2﹣x≥0的否定形式是特称命题;
“ x∈R,x2﹣x<0”.
故选:D
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,若用系统抽样方法,则所抽取的编号可能是( )
A.2,4,6,8
B.2,6,10,14
C.2,7,12,17
D.5,8,9,14
【考点】系统抽样方法.
【分析】根据系统抽样的定义确定样本数据的组距即可得到结论.
【解答】解:从20位同学,编号从1至20,现在从中抽取4人作问卷调查,则组距为20÷4=5,
则4个号码差距为5.
则满足条件的号码可能是2,7,12,17.
故选:C.
3.曲线y=与直线y=x﹣1及x=4所围成的封闭图形的面积为( )
A.2ln
2
B.2﹣ln
2
C.4﹣ln
2
D.4﹣2ln
2
【考点】定积分.
【分析】先联立两个曲线的方程,求出
( http: / / www.21cnjy.com )交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.先联立两个曲线的方程,求出交点,以确定积分公式中x的取值范围,最后根据定积分的几何意义表示出区域的面积,根据定积分公式解之即可.
【解答】解:由曲线y=与直线y=x﹣1联立,解得,x=﹣1,x=2,
故所求图形的面积为S=(x﹣1﹣)dx=(x2﹣x﹣2lnx)|=4﹣2ln2.
故选:C.
4.抛物线y=4x2的焦点坐标是( )
A.(0,1)
B.(1,0)
C.
D.
【考点】抛物线的简单性质.
【分析】把抛物线y=4x2的方程化为标准形式,确定开口方向和p值,即可得到焦点坐标.
【解答】解:抛物线y=4x2的标准方程为
x2=y,p=,开口向上,焦点在y轴的正半轴上,
故焦点坐标为(0,),
故选C.
5.函数f(x)=x2﹣2lnx的单调减区间是( )
A.(0,1)
B.(1,+∞)
C.(﹣∞,﹣1)∪(0,1)
D.(﹣1,0)∪(0,1)
【考点】利用导数研究函数的单调性.
【分析】依题意,可求得f′(x),由f′(x)<0即可求得函数f(x)=x2﹣2lnx的单调减区间.
【解答】解:∵f(x)=x2﹣2lnx(x>0),
∴f′(x)=2x﹣=,
令f′(x)<0由图得:0<x<1,
∴函数f(x)=x2﹣2lnx的单调减区间是(0,1),
故选:A.
6.在空间四边形OABC中,,,,点M在线段OA上,且OM=2MA,N为BC的中点,则等于( )
A.
﹣+
B.﹣++
C.
D.
【考点】向量加减混合运算及其几何意义.
【分析】由题意结合图形,直接利用,求出,然后即可解答.
【解答】解:因为空间四边形OABC如图,,,,
点M在线段OA上,且OM=2MA,N为BC的中点,
所以=.
所以=.
故选B.
7.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
【考点】循环结构;设计程序框图解决实际问题.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S值.
【解答】解:程序运行过程中,各变量的值如下表示:
i
S
是否继续循环
循环前
1
1/
第一圈
2
4
是
第二圈
3
10
是
第三圈
4
22
是
第四圈
5
46
是
第五圈
6
94
否
故输入的S值为94
故选C.
8.“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据椭圆的性质,结合充分条件和必要条件的定义进行判断即可.
【解答】解:若方程+=1表示的曲线是焦点在y轴上的椭圆,
则,
即,
解得1<m<2,即“1<m<2”是“方程+=1表示的曲线是焦点在y轴上的椭圆”的充要条件,
故选:C
9.有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题;
②“全等三角形的面积相等”的否命题;
③“若“q≤1”,则x2+2x+q=0有实根”的逆否命题;
④“矩形的对角线相等”的逆命题.
其中真命题为( )
A.①②
B.①③
C.②③
D.③④
【考点】命题的真假判断与应用.
【分析】①由于“若a2+b2=0,则a,b全为0”是真命题,由于逆否命题与原命题是等价命题,即可判断出;
②“全等三角形的面积相等”的否命题为“不全等的三角形的面积不相等”,是假命题;
③若x2+2x+q=0有实根,则△=4﹣4q≥0,解得q≤1,即可判断出;
④“矩形的对角线相等”的逆命题为“对角线相等的四边形是矩形”,即可判断出.
【解答】解:①由于“若a2+b2=0,则a,b全为0”是真命题,因此其逆否命题是真命题;
②“全等三角形的面积相等”的否命题为“不全等的三角形的面积不相等”,不正确;
③若x2+2x+q=0有实根,则△=4﹣4q≥0,解得q≤1,因此“若“q≤1”,则x2+2x+q=0有实根”的逆否命题是真命题;
④“矩形的对角线相等”的逆命题为“对角线相等的四边形是矩形”,是假命题.
综上可得:真命题为:①③.
故选:B.
10.如果双曲线的离心率等于2,则实数m等于( )
A.6
B.14
C.4
D.8
【考点】双曲线的简单性质.
【分析】直接求出双曲线的实轴长,焦距的长,然后利用双曲线的离心率,求出m值.
【解答】解:因为双曲线为,所以2a=2,b=,
所以c=,因为双曲线的离心率等于2,
所以2=,所以m=6.
故选A.
11.如图,“天宫一号”运行的轨迹是如图的两
( http: / / www.21cnjy.com )个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
A.
B.
C.
D.
【考点】几何概型.
【分析】点P与点O的距离小
( http: / / www.21cnjy.com )于3cm,也就是说以O点为圆心,3CM为半径作一个圆,这个圆的面积减去小圆的面积就是点P与点O的距离小于3cm的机会(一个圆环的面积),而P可能落在的面积为大圆面积减小圆面积,也就是整个圆环的面积,点P与点O距离小于3cm的概率=小圆环的面积:大圆环的面积.
【解答】解:如图所示,
S大圆环=42π﹣22π=12π,
S小圆环=32π﹣22π=5π,
所以,点P与点O距离小于3cm的概率==.
故选B.
12.已知函数y=f(x
( http: / / www.21cnjy.com ))对任意的x∈(﹣,)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.
f(﹣)<f(﹣)
B.
f()<f()
C.f(0)>2f()
D.f(0)>f()
【考点】利用导数研究函数的单调性.
【分析】根据条件构造函数g(x)=,求函数的导数,利用函数的单调性和导数之间的关系即可得到结论.
【解答】解:构造函数g(x)=,
则g′(x)==(f′(x)cosx+f(x)sinx),
∵对任意的x∈(﹣,)满足f′(x)cosx+f(x)sinx>0,
∴g′(x)>0,即函数g(x)在x∈(﹣,)单调递增,
则g(﹣)<g(﹣),即,
∴,即f(﹣)<f(﹣),故A正确.
g(0)<g(),即,
∴f(0)<2f(),
故选:A.
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.
13.由定积分的几何意义可知dx= 2π .
【考点】定积分.
【分析】本题利用定积分的几何意义计算定积分,即求被积函数y=与x轴所围成的图形的面积即可.
【解答】解:根据定积分的几何意义,则
dx表示圆心在原点,半径为2的圆的上半圆的面积,
故
dx=×π×22=2π.
故答案为:2π.
14.已知p:(x+2)(x﹣3)≤0,q:|x+1|≥2,命题“p∧q”为真,则实数x的取值范围是 [1,3] .
【考点】复合命题的真假.
【分析】分别解出p,q的x的范围,再利用命题“p∧q”为真即可得出.
【解答】解:p:(x+2)(x﹣3)≤0,解得﹣2≤x≤3.
q:|x+1|≥2,解得x≥1或x≤﹣3.
命题“p∧q”为真,∴,解得1≤x≤3.
则实数x的取值范围是[1,3].
故答案为:[1,3].
15.椭圆+y2=1中,以点M(1,)为中点的弦所在直线方程是 x+2y﹣2=0 .
【考点】椭圆的简单性质.
【分析】判断M在椭圆内,设弦AB的端点
( http: / / www.21cnjy.com )为(x1,y1),(x2,y2),代入椭圆方程,运用点差法,结合直线的斜率公式和中点坐标公式,再由点斜式方程,即可得到所求方程.
【解答】解:由M点代入椭圆方程可得,
+<1,
即M在椭圆内,则直线与椭圆相交.
设弦AB的端点为(x1,y1),(x2,y2),
即有+y12=1,
+y22=1,
两式相减可得,
+(y1﹣y2)(y1+y2)=0,
由中点坐标公式可得,x1+x2=2,y1+y2=1,
代入上式,可得kAB==﹣=﹣,
即有弦所在的直线方程为y﹣=﹣(x﹣1),
即为x+2y﹣2=0.
故答案为:x+2y﹣2=0.
16.已知方程﹣=0有两个不等的非零根,则a的取值范围是 (0,) .
【考点】根的存在性及根的个数判断.
【分析】由方程﹣=0得a=,x≠0;再令f(x)=,从而求导f′(x)=以确定函数的单调性及取值,从而确定a的取值范围.
【解答】解:由方程﹣=0得,
a=,x≠0;
令f(x)=,
则f′(x)=;
故f(x)在(﹣∞,1)上是增函数,且f(x)<f(1)=;
在(1,+∞)上是减函数,且0<f(x)<;
故若方程﹣=0有两个不等的非零根,
则a的取值范围是(0,).
故答案为:(0,).
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
【考点】回归分析的初步应用.
【分析】(1)根据表中所给的数据,做出
( http: / / www.21cnjy.com )横标和纵标的平均数,得到样本中心点,求出对应的横标和纵标的积的和,求出横标的平方和,做出系数和a的值,写出线性回归方程.
(2)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05.试预测加工10个零件需要8.05个小时,这是一个预报值.
【解答】解:(1)由表中数据得:
xiyi=52.5,
=3.5,
=3.5,
xi2=54.
∴b==0.7
故a=3.5﹣0.7×3.5=1.05,
∴所求线性回归方程为:y=0.7x+1.05.
(2)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时).
∴试预测加工10个零件需要8.05个小时.
18.已知函数f(x)=2x3+3x2﹣12x+5.
(Ⅰ)求曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)求函数f(x)的极值.
【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的极值.
【分析】(Ⅰ)求出函数的导数在x=0的导数值,就是切线的斜率,利用点斜式求解曲线y=f(x)在点(0,5)处的切线方程;
(Ⅱ)利用函数的导数为0,求出极值点,判断导函数的符号,即可求函数f(x)的极值.
【解答】(本小题满分12分)
解:f′(x)=6x2+6x﹣12…
(Ⅰ)依题意可知:k=f′(x)|x=0=﹣12…
∴切线方程为:y﹣5=﹣12x
即12x+y﹣5=0…
(Ⅱ)令f′(x)=0,得:x1=﹣2,x2=1…
x
(﹣∞,﹣2)
﹣2
(﹣2,1)
1
(1,+∞)
f'(x)
+
0
﹣
+
f(x)
↑
极大值25
↓
极小值﹣2
↑
…
∴f(x)的极大值为f(﹣2)=25,极小值为f(1)=﹣2…
19.已知四棱锥P﹣ABCD中PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,
∠CDA=∠BAD=90°,,M,N分别是PD,PB的中点.
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离.
【考点】与二面角有关的立体几何综合题;直线与平面平行的判定;点、线、面间的距离计算.
【分析】此类题一般有两种解法,一种是利用空间向量方法来证明,一种是用立体几何中线面位置关系进行证明,本题提供两种解法
向量法:对于(1)求证:MQ∥平面PCB,可求出线的方向向量与面的法向量,如果两者的内积为0则说明线面平行
对于(2)求截面MCN与底面ABCD所成二面角的大小,求出两个平面的法向量,然后根据根据二面角的正弦与法向量的数量积的关系,求解;
对于(3)求点A到平面MCN的距离
( http: / / www.21cnjy.com ),求出平面上任一点与A连线所对应的向量,求这个向量在该平面的法向量上的投影即可,此法求点到面的距离甚为巧妙.
几何法:(1)求证MQ∥平面PCB,用线面平行的判定定理证明即可;
(2)求截面MCN与底面ABCD所成二面
( http: / / www.21cnjy.com )角的大小,先在图形中作出二面角的平面角,再证明其是二面角的平面角,然后根据题设中的条件求出平面角的三角函数值,一般要在一个三角形中求解函数值.
(3)求点A到平面MCN的距离,须先作出点A在面上的垂线段,然后在三角形中求出此线段的长度即可.
【解答】解:法一向量法:
以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O﹣xyz,
由,PA=4PQ=4,M,N分别是PD,PB的中点,
可得:,
∴,
设平面的PBC的法向量为,
则有:
令z=1,则,
∴,
又MQ 平面PCB,∴MQ∥平面PCB;
(2)设平面的MCN的法向量为,又
则有:
令z=1,则,
又为平面ABCD的法向量,
∴,又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为,
(3)∵,∴所求的距离;
法二,几何法:
(1)取AP的中点E,连接ED,则ED∥CN,依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,
又MQ 平面PCB,CN 平面PCB,∴MQ∥平面PCB
(2)易证:平面MEN∥底面ABCD,所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的二面角,
因为PA⊥平面ABCD,所以PA⊥平面MEN,过E做EF⊥MN,垂足为F,连接QF,
则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面所以∠QFE为截面MCN与平面MEN所成的二面角的平面角,,
所以:,
所以:;
(3)因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,
由(2)知:MN⊥平面QEF,则平面
( http: / / www.21cnjy.com )MCNQ⊥平面QEF且交线为QF,作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.
.
20.某校从高二年级学生中随机抽取40
( http: / / www.21cnjy.com )名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,5
( http: / / www.21cnjy.com )0)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
【考点】古典概型及其概率计算公式;频率分布直方图.
【分析】(1)根据阴影矩形的面积之和等于1,计算a的值;
(2)首先计算成绩不低于60分的频率,即后四个小矩形的面积和,然后用640×频率计算人数;
(3)若两名学生的学生成绩之差的绝对值
( http: / / www.21cnjy.com )不大于10,即两人是同一组的学生,那么首先计算两组的人数,并编号,并以编号的形式列出所有选取2人的基本事件的个数,同时计算同一组的两个人的所有基本事件的个数,最后相除得到概率.
【解答】(1)解:由于图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03.
(2)解:根据频率分布直方图,成绩不低于6的频率为
1﹣10×(0.005+0.01)=0.85.
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于6的人数约为640×0.85=544人.
(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:
(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
所以所求概率为P(M)=.
21.围建一个面积为360m2的矩形场地,
( http: / / www.21cnjy.com )要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
【考点】函数模型的选择与应用;函数的值域;基本不等式在最值问题中的应用.
【分析】(I)设矩形的另一边
( http: / / www.21cnjy.com )长为am,则根据围建的矩形场地的面积为360m2,易得,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;
(II)根据(I)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值.
【解答】解:(Ⅰ)设矩形的另一边长为am,
则y=45x+180(x﹣2)+180 2a=225x+360a﹣360.
由已知ax=360,得,
所以.
(II)因为x>0,所以,
所以,当且仅当时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
22.已知椭圆C:
=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点
M,N.
(1)求椭圆C的方程,并求其焦点坐标;
(2)当△AMN的面积为时,求k的值.
【考点】椭圆的简单性质.
【分析】(1)由题意可得:a=2,,a2=b2+c2,联立解得即可得出.
(2)设M(x1,y1),N(x2,y
( http: / / www.21cnjy.com )2),直线方程与椭圆方程联立化为:(1+2k2)x2﹣4k2x+2k2﹣4=0,利用根与系数的关系可得|MN|=,点A到直线MN的距离d.利用△AMN的面积==|MN|,解出即可得出.
【解答】解:(1)由题意可得:a=2,,a2=b2+c2,联立解得a=2,c=b=.
∴椭圆C的标准方程为:
=1,其焦点坐标为:.
(2)设M(x1,y1),N(x2,y2),联立,
化为:(1+2k2)x2﹣4k2x+2k2﹣4=0,
△>0,∴x1+x2=,x1x2=.
∴|MN|=
==.
点A到直线MN的距离d=.
∴△AMN的面积==|MN|=,
化为:20k4﹣7k2﹣13=0,
解得k2=1,解得k=±1.
2017年3月8日
