云南省昭通市云天化中学2016-2017学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 云南省昭通市云天化中学2016-2017学年高二(上)期末数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 344.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 15:31:02 | ||
图片预览




文档简介
2016-2017学年云南省昭通市云天化中学高二(上)期末数学试卷(文科)
一、选择题:(每小题5分,共60分.每小题只有一个选项符合题意.)
1.直线x=1的倾斜角是( )
A.0
B.
C.
D.不存在
2.高二某班共有学生56人,座号分别为1
( http: / / www.21cnjy.com ),2,3,…,56现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知4号、18号、46号同学在样本中,那么样本中还有一个同学的座号是( )
A.30
B.31
C.32
D.33
3.同时抛掷两枚骰子,向上点数之和为5的概率是( )
A.
B.
C.
D.
4.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
A.﹣14
B.﹣7
C.7
D.14
5.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
6.已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
A.6π+12
B.6π+24
C.12π+12
D.24π+12
7.甲、乙两名选手参加歌手大赛时,5名评委
( http: / / www.21cnjy.com )打的分数,用茎叶图表示(如图)s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是(填“>”、“<”或“=”)( )
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
8.已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:2(k﹣3)x﹣2y+3=0平行,则k的值是( )
A.1或3
B.1或5
C.3或5
D.1或2
9.为了了解某校九年级1600名学生的体能
( http: / / www.21cnjy.com )情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
10.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( )
A.
B.
C.2
D.
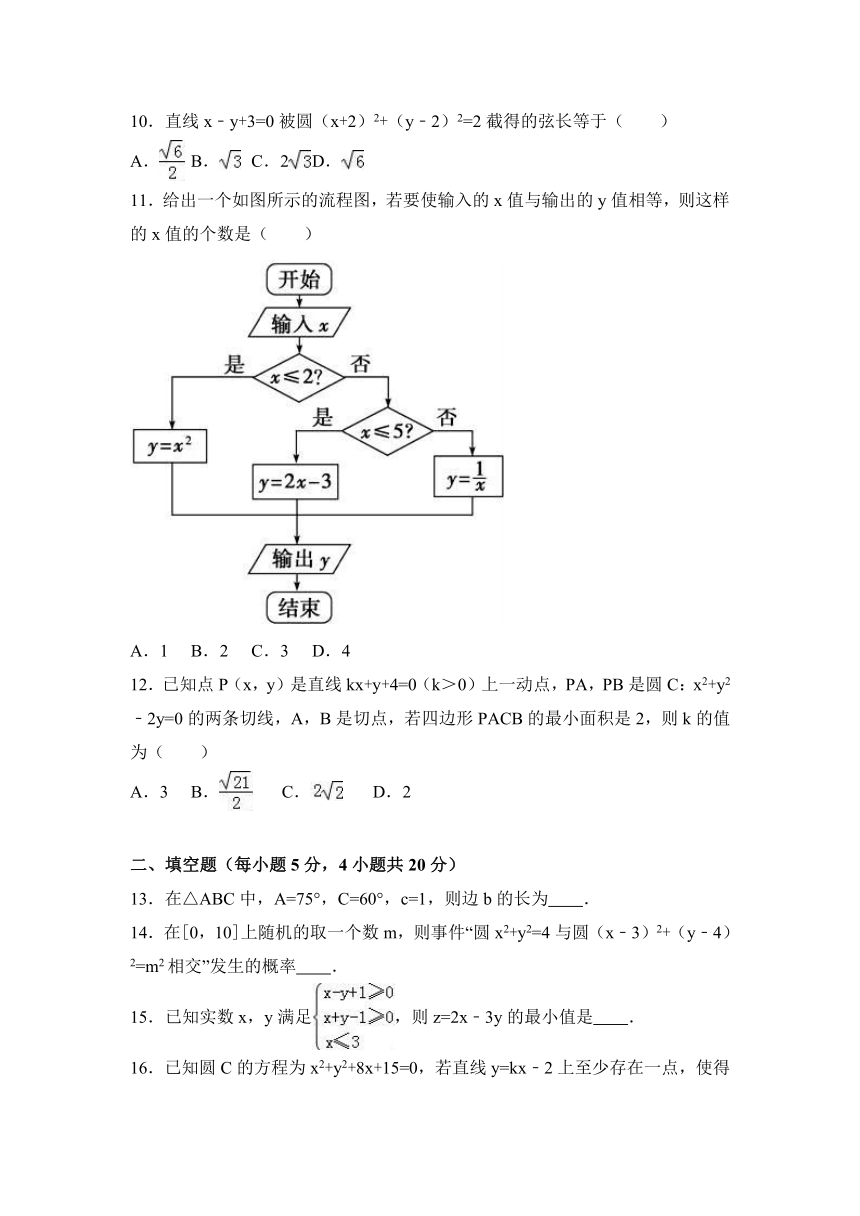
11.给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是( )
A.1
B.2
C.3
D.4
12.已知点P(x,y)是
( http: / / www.21cnjy.com )直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2﹣2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为( )
A.3
B.
C.
D.2
二、填空题(每小题5分,4小题共20分)
13.在△ABC中,A=75°,C=60°,c=1,则边b的长为 .
14.在[0,10]上随机的取一个数m,则事件“圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2相交”发生的概率 .
15.已知实数x,y满足,则z=2x﹣3y的最小值是 .
16.已知圆C的方程为x2+y2+8x
( http: / / www.21cnjy.com )+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围为 .
三、解答题(第17题10分,其余每题12分,共70分,解答应写出证明过程或演算步骤)
17.某市有M,N,S三所高校,其
( http: / / www.21cnjy.com )学生会学习部有“干事”人数分别为36,24,12,现采用分层抽样的方法从这些“干事”中抽取6名进行“大学生学习部活动现状”调查.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
18.下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
)
(参考公式:
=;;)
19.已知正方形ABCD的边长为1,如图所示:
(1)在正方形内任取一点,求事件“|AM|≤1”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形BAD内,请据此估计圆周率π的近似值(精确到0.001).
20.设△ABC的内角A,B,C所对应的边长分别是a,b,c且cosB=,b=2
(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
21.设函数.
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当时,函数f(x)的最大值与最小值的和为,求a的值.
22.已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
2016-2017学年云南省昭通市云天化中学高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(每小题5分,共60分.每小题只有一个选项符合题意.)
1.直线x=1的倾斜角是( )
A.0
B.
C.
D.不存在
【考点】直线的倾斜角.
【分析】由于直线x=1与x轴垂直,即可得出直线的倾斜角.
【解答】解:∵直线x=1与x轴垂直,因此倾斜角是.
故选:C.
2.高二某班共有学生56人,座号分
( http: / / www.21cnjy.com )别为1,2,3,…,56现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知4号、18号、46号同学在样本中,那么样本中还有一个同学的座号是( )
A.30
B.31
C.32
D.33
【考点】系统抽样方法.
【分析】根据系统抽样原理求出抽样间隔,由第一组抽出的学号得出每组抽出的学号是什么.
【解答】解:根据系统抽样原理得,抽样间隔是=14,
且第一组抽出的学号为4,
那么每组抽出的学号为4+14(n﹣1),其中n=1、2、3、4;
所以第二组抽取的学号为4+14×2=32.
故选C.
3.同时抛掷两枚骰子,向上点数之和为5的概率是( )
A.
B.
C.
D.
【考点】列举法计算基本事件数及事件发生的概率.
【分析】利用列举法得到同时向上掷两枚骰子,向
( http: / / www.21cnjy.com )上的点数之和共有36种结果,而向上的点数之和为5的结果有4种情况,由此能求出向上的点数之和等于5的概率.为.
【解答】解:抛掷两颗骰子所出现的不同结果数是6×6=36
事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”所包含的基本事件有(1,4),(2,3),(3,2),(4,1)共四种
故事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”的概率是=,
故选:A.
4.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
A.﹣14
B.﹣7
C.7
D.14
【考点】等差数列的通项公式.
【分析】利用等差数列的通项公式及其性质即可得出.
【解答】解:∵a3+a6=11,a5+a8=39,则4d=28,解得d=7.
故选:C.
5.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
【考点】循环结构;设计程序框图解决实际问题.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S值.
【解答】解:程序运行过程中,各变量的值如下表示:
i
S
是否继续循环
循环前
1
1/
第一圈
2
4
是
第二圈
3
10
是
第三圈
4
22
是
第四圈
5
46
是
第五圈
6
94
否
故输入的S值为94
故选C.
6.已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
A.6π+12
B.6π+24
C.12π+12
D.24π+12
【考点】由三视图求面积、体积.
【分析】由三视图可知几何体为半圆柱与直三棱柱的组合体,利用体积公式,即可得出结论.
【解答】解:由三视图可知几何体为半圆柱与直三棱柱的组合体,
V==6π+12,
故选A.
7.甲、乙两名选手参加歌手
( http: / / www.21cnjy.com )大赛时,5名评委打的分数,用茎叶图表示(如图)s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是(填“>”、“<”或“=”)( )
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
【考点】茎叶图;极差、方差与标准差.
【分析】首先做出两个选手
( http: / / www.21cnjy.com )的平均分,结果两个选手的平均分相同,观察两个人的分数在茎叶图中甲的分数是单峰的,比较集中,而乙的分数是双峰的,比较分散,由茎叶图的性质可得答案.
【解答】解:甲选手的平均分是=84
乙选手的平均分是=84
这两个选手的平均分是相同的,
从茎叶图上看甲的分数是单峰的,分数比较集中,
乙的分数是双峰的,分数分散,
∴甲的方差一定小于乙的方差,
故选C.
8.已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:2(k﹣3)x﹣2y+3=0平行,则k的值是( )
A.1或3
B.1或5
C.3或5
D.1或2
【考点】直线的一般式方程与直线的平行关系.
【分析】当k﹣3=0时,求出两直线的方程,检验是否平行;当k﹣3≠0时,由一次项系数之比相等且不等于常数项之比,求出k的值.
【解答】解:由两直线平行得,当k﹣3=0时,两直线的方程分别为
y=﹣1
和
y=,显然两直线平行.
当k﹣3≠0时,由
=≠,可得
k=5.综上,k的值是
3或5,
故选
C.
9.为了了解某校九年级1600名学生的
( http: / / www.21cnjy.com )体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
【考点】频率分布直方图.
【分析】根据频率=小矩形的高×组距,求得第一组,第二组,第三组的频率,利用中位数的左,右两边频率相等求得中位数;验证A是否正确.
根据最高矩形的底边中点的横坐标为数据的众数求得众数;验证B是否正确;
利用频率=小矩形的高×组距=求1分钟仰卧起坐的成绩超过30次的频数和1分钟仰卧起坐的成绩少于20次的频数,由此可验证C、D是否正确.
【解答】解:第一组数据的频率为0.02×5=0.1;第二组数据的频率为0.06×5=0.3,第三组的频率为0.08×5=0.4,
∴中位数在第三组内,设中位数为25+x
( http: / / www.21cnjy.com ),则x×0.08=0.5﹣0.1﹣0.3=0.1,∴x=1.25,∴数据的中位数为26.25,故A正确;
最高矩形是第三组数据,第三组数据的中间值为27.5,∴众数为27.5,故B正确;
学生1分钟仰卧起坐的成绩超过30次的频率为0.04×5=0.2,∴超过30次的人数为1600×0.2=320人,故C正确;
学生1分钟仰卧起坐的成绩少于20次
( http: / / www.21cnjy.com )的频率为0.02×5=0.1,∴1分钟仰卧起坐的成绩少于20次的人数为1600×0.1=160人,故D错误.
故选:D.
10.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( )
A.
B.
C.2
D.
【考点】直线和圆的方程的应用.
【分析】先根据点到直线的距离公式求出圆心
( http: / / www.21cnjy.com )到弦的距离即弦心距OD,然后根据垂径定理得到垂足为弦长的中点D,根据勾股定理求出弦长的一半BD,乘以2即可求出弦长AB.
【解答】解:连接OB,过O作OD⊥AB,根据垂径定理得:D为AB的中点,
根据(x+2)2+(y﹣2)2=2得到圆心坐标为(﹣2,2),半径为.
圆心O到直线AB的距离OD==,而半径OB=,
则在直角三角形OBD中根据勾股定理得BD==,所以AB=2BD=
故选D.
11.给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是( )
A.1
B.2
C.3
D.4
【考点】选择结构.
【分析】由已知的流程图,我们易得这是
( http: / / www.21cnjy.com )一个计算并输出分段函数函数值的程序,我们根据条件,分x≤2,2<x≤5,x>5三种情况分别讨论,满足输入的x值与输出的y值相等的情况,即可得到答案.
【解答】解:当x≤2时,由x2=x得:x=0,1满足条件;
当2<x≤5时,由2x﹣3=x得:x=3,满足条件;
当x>5时,由=x得:x=±1,不满足条件,
故这样的x值有3个.
故选C.
12.已知点P(x,y)是直线kx+y
( http: / / www.21cnjy.com )+4=0(k>0)上一动点,PA,PB是圆C:x2+y2﹣2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为( )
A.3
B.
C.
D.2
【考点】直线和圆的方程的应用.
【分析】先求圆的半径,四边形P
( http: / / www.21cnjy.com )ACB的最小面积是2,转化为三角形PBC的面积是1,求出切线长,再求PC的距离也就是圆心到直线的距离,可解k的值.
【解答】解:圆C:x2+y2﹣2y=0的圆心(0,1),半径是r=1,
由圆的性质知:S四边形PACB=2S△PBC,四边形PACB的最小面积是2,
∴S△PBC的最小值=1=rd(d是切线长)∴d最小值=2
圆心到直线的距离就是PC的最小值,
∵k>0,∴k=2
故选D.
二、填空题(每小题5分,4小题共20分)
13.在△ABC中,A=75°,C=60°,c=1,则边b的长为 .
【考点】余弦定理.
【分析】由已知及三角形内角和定理可求B的值,进而利用正弦定理可求b的值.
【解答】解:∵A=75°,C=60°,c=1,
∴B=180°﹣A﹣C=45°,
∴由正弦定理可得:b===.
故答案为:.
14.在[0,10]上随机的取一个数m,则事件“圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2相交”发生的概率 .
【考点】几何概型.
【分析】计算两圆的圆心距d,利用两圆相交R﹣r<d<R+r,求出m的取值范围,再利用几何概型计算对应的概率值.
【解答】解:圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2的圆心距为
d==5,
若两圆相交,则,
解得3<m<7;
所以,两圆相交时发生的概率为:
P==.
故答案为:.
15.已知实数x,y满足,则z=2x﹣3y的最小值是 ﹣6 .
【考点】简单线性规划.
【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,分类代入目标函数求解.
【解答】解:由约束条件作出可行域如图,
联立,解得A(3,4).
化目标函数z=2x﹣3y为.
由图可知,当直线过A时,直线在y轴上的截距最大,z有最小值为2×3﹣3×4=﹣6.
故答案为:﹣6.
16.已知圆C的方程为x2+y2+8x
( http: / / www.21cnjy.com )+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围为 .
【考点】圆的一般方程.
【分析】将圆C的方程整理为标准形式,找出圆
( http: / / www.21cnjy.com )心C的坐标与半径r,根据直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,即圆心到直线y=kx﹣2的距离小于等于2,利用点到直线的距离公式列出关于k的不等式求出不等式的解集即可得到k的范围.
【解答】解:将圆C的方程整理为标准方程得:(x+4)2+y2=1,
∴圆心C(﹣4,0),半径r=1,
∵直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴圆心(﹣4,0)到直线y=kx﹣2的距离d=,
解得:≤k≤0.
故答案为:.
三、解答题(第17题10分,其余每题12分,共70分,解答应写出证明过程或演算步骤)
17.某市有M,N,S三所高
( http: / / www.21cnjy.com )校,其学生会学习部有“干事”人数分别为36,24,12,现采用分层抽样的方法从这些“干事”中抽取6名进行“大学生学习部活动现状”调查.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
【考点】古典概型及其概率计算公式;分层抽样方法.
【分析】(Ⅰ)求出抽样比,即可从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)在抽取到的6名干事中,来自高校M
( http: / / www.21cnjy.com )的3名分别记为1、2、3,来自高校N的2名分别记为a、b,来自高校S的1名记为c,写出选出2名干事的所有可能结果,设A={所选2名干事来自同一高校},写出事件A的所有可能结果,利用古典概型求解即可.
【解答】解:(Ⅰ)抽样比为:,
故应从M,N,S这三所高校抽取的“干事”人数分别为3,2,1;
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,
来自高校N的2名分别记为a、b,来自高校S的1名记为c,
则选出2名干事的所有可能结果为:
{1,2},{1,3},{1,a
},{1,b
},{1,c},
{2,3},{2,a},{2,b},{2,c},
{3,a},{3,b
},{3,c
},
{
a,b
},{
a,c
},
{
b,c}共15种.
设A={所选2名干事来自同一高校},
事件A的所有可能结果为{1,2},{1,3},{2,3},{a,b},共4种,
所以.
18.下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
)
(参考公式:
=;;)
【考点】线性回归方程.
【分析】(1)由题意易得散点图:
(2)由已知数据求出=4,
=5,
=90,结合参考数据可得和,可得回归直线方程;
(3)把x=10代入(2)中的方程计算可得;
【解答】解:(1)由题意可得散点图如图:
(2)从散点图可知,变量y与x之间有较强的线性相关性.
由已知数据有:
=4,
=5,
=90,
又由参考数据知
∴===1.23,
∴=﹣=5﹣1.23×4=0.08,
∴回归直线方程为=1.23x+0.08;
(3)当x=10时,维修费用=1.23×10+0.08=12.38(万元)
19.已知正方形ABCD的边长为1,如图所示:
(1)在正方形内任取一点,求事件“|AM|≤1”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形BAD内,请据此估计圆周率π的近似值(精确到0.001).
【考点】模拟方法估计概率.
【分析】(1)根据已知条件,求出满足条
( http: / / www.21cnjy.com )件的正方形ABCD的面积,及事件“|AM|≤1”对应平面区域的面积,代入几何概型计算公式,即可求出答案.
(2)正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内,频率为,用频率估计概率,由(1)知,可得圆周率π的近似值.
【解答】解:(1)如图,在边长为1的正方
( http: / / www.21cnjy.com )形ABCD内任取一点M,满足条件的点M落在扇形BAD内(图中阴影部分),由几何概型概率计算公式,有:,
故事件“|AM|≤1”发生的概率为.
(2)正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内,频率为,
用频率估计概率,由(1)知,
∴,即π的近似值为3.143.
20.设△ABC的内角A,B,C所对应的边长分别是a,b,c且cosB=,b=2
(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
【考点】余弦定理;正弦定理.
【分析】(Ⅰ)由cosB=,B∈(0,π),可得sinB=,再利用正弦定理即可得出.
(Ⅱ)由S△ABC==3,可得ac=.再利用余弦定理即可得出.
【解答】解:(Ⅰ)∵cosB=,B∈(0,π),
∴sinB==,
由正弦定理可知:,
∴a=.
(Ⅱ)∵S△ABC===3,
∴ac=.
由余弦定理得:b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣2ac×=4,
∴(a+c)2=+4=28,
故:a+c=2.
21.设函数.
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当时,函数f(x)的最大值与最小值的和为,求a的值.
【考点】三角函数的恒等变换及化简求值;三角函数的周期性及其求法;正弦函数的定义域和值域;正弦函数的单调性.
【分析】(1)根据二倍角公式,和辅助角公式,我们易将函数的解析化简为正弦型函数的形式,进而求出函数f(x)的最小正周期及单调递减区间;
(2)当时,根据函数f(x)的最大值与最小值的和为,我们可构造出关于a的方程,解方程即可得到a的值.
【解答】解(1),
∴T=π.
.
故函数f(x)的单调递减区间是.
(2)∵,∴.∴.
当时,原函数的最大值与最小值的和=,∴a=0
22.已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
【考点】等差数列与等比数列的综合.
【分析】(I)将已知等式用等差数列{an}的首项、公差表示,列出方程组,求出首项、公差;利用等差数列的通项公式求出数列{an}的通项公式.
(II)利用等比数列的通项公式求出,进一步求出bn,根据数列{bn}通项的特点,选择错位相减法求出数列{bn}的前n项和Tn.
【解答】解:(Ⅰ)依题意得
解得,
∴an=a1+(n﹣1)d=3+2(n﹣1)=2n+1,
即an=2n+1.
(Ⅱ),
bn=an 3n﹣1=(2n+1) 3n﹣1
Tn=3+5 3+7 32+…+(2n+1) 3n﹣1
3Tn=3 3+5 32+7 33+…+(2n﹣1) 3n﹣1+(2n+1) 3n
﹣2Tn=3+2 3+2 32+…+2 3n﹣1﹣(2n+1)3n
∴Tn=n 3n.
2017年3月8日
一、选择题:(每小题5分,共60分.每小题只有一个选项符合题意.)
1.直线x=1的倾斜角是( )
A.0
B.
C.
D.不存在
2.高二某班共有学生56人,座号分别为1
( http: / / www.21cnjy.com ),2,3,…,56现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知4号、18号、46号同学在样本中,那么样本中还有一个同学的座号是( )
A.30
B.31
C.32
D.33
3.同时抛掷两枚骰子,向上点数之和为5的概率是( )
A.
B.
C.
D.
4.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
A.﹣14
B.﹣7
C.7
D.14
5.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
6.已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
A.6π+12
B.6π+24
C.12π+12
D.24π+12
7.甲、乙两名选手参加歌手大赛时,5名评委
( http: / / www.21cnjy.com )打的分数,用茎叶图表示(如图)s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是(填“>”、“<”或“=”)( )
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
8.已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:2(k﹣3)x﹣2y+3=0平行,则k的值是( )
A.1或3
B.1或5
C.3或5
D.1或2
9.为了了解某校九年级1600名学生的体能
( http: / / www.21cnjy.com )情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
10.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( )
A.
B.
C.2
D.
11.给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是( )
A.1
B.2
C.3
D.4
12.已知点P(x,y)是
( http: / / www.21cnjy.com )直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2﹣2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为( )
A.3
B.
C.
D.2
二、填空题(每小题5分,4小题共20分)
13.在△ABC中,A=75°,C=60°,c=1,则边b的长为 .
14.在[0,10]上随机的取一个数m,则事件“圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2相交”发生的概率 .
15.已知实数x,y满足,则z=2x﹣3y的最小值是 .
16.已知圆C的方程为x2+y2+8x
( http: / / www.21cnjy.com )+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围为 .
三、解答题(第17题10分,其余每题12分,共70分,解答应写出证明过程或演算步骤)
17.某市有M,N,S三所高校,其
( http: / / www.21cnjy.com )学生会学习部有“干事”人数分别为36,24,12,现采用分层抽样的方法从这些“干事”中抽取6名进行“大学生学习部活动现状”调查.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
18.下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
)
(参考公式:
=;;)
19.已知正方形ABCD的边长为1,如图所示:
(1)在正方形内任取一点,求事件“|AM|≤1”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形BAD内,请据此估计圆周率π的近似值(精确到0.001).
20.设△ABC的内角A,B,C所对应的边长分别是a,b,c且cosB=,b=2
(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
21.设函数.
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当时,函数f(x)的最大值与最小值的和为,求a的值.
22.已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
2016-2017学年云南省昭通市云天化中学高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(每小题5分,共60分.每小题只有一个选项符合题意.)
1.直线x=1的倾斜角是( )
A.0
B.
C.
D.不存在
【考点】直线的倾斜角.
【分析】由于直线x=1与x轴垂直,即可得出直线的倾斜角.
【解答】解:∵直线x=1与x轴垂直,因此倾斜角是.
故选:C.
2.高二某班共有学生56人,座号分
( http: / / www.21cnjy.com )别为1,2,3,…,56现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知4号、18号、46号同学在样本中,那么样本中还有一个同学的座号是( )
A.30
B.31
C.32
D.33
【考点】系统抽样方法.
【分析】根据系统抽样原理求出抽样间隔,由第一组抽出的学号得出每组抽出的学号是什么.
【解答】解:根据系统抽样原理得,抽样间隔是=14,
且第一组抽出的学号为4,
那么每组抽出的学号为4+14(n﹣1),其中n=1、2、3、4;
所以第二组抽取的学号为4+14×2=32.
故选C.
3.同时抛掷两枚骰子,向上点数之和为5的概率是( )
A.
B.
C.
D.
【考点】列举法计算基本事件数及事件发生的概率.
【分析】利用列举法得到同时向上掷两枚骰子,向
( http: / / www.21cnjy.com )上的点数之和共有36种结果,而向上的点数之和为5的结果有4种情况,由此能求出向上的点数之和等于5的概率.为.
【解答】解:抛掷两颗骰子所出现的不同结果数是6×6=36
事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”所包含的基本事件有(1,4),(2,3),(3,2),(4,1)共四种
故事件“抛掷两颗骰子,所得两颗骰子的点数之和为5”的概率是=,
故选:A.
4.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
A.﹣14
B.﹣7
C.7
D.14
【考点】等差数列的通项公式.
【分析】利用等差数列的通项公式及其性质即可得出.
【解答】解:∵a3+a6=11,a5+a8=39,则4d=28,解得d=7.
故选:C.
5.如果执行如图的程序框图,那么输出的S=( )
A.22
B.46
C.94
D.190
【考点】循环结构;设计程序框图解决实际问题.
【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S值.
【解答】解:程序运行过程中,各变量的值如下表示:
i
S
是否继续循环
循环前
1
1/
第一圈
2
4
是
第二圈
3
10
是
第三圈
4
22
是
第四圈
5
46
是
第五圈
6
94
否
故输入的S值为94
故选C.
6.已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
A.6π+12
B.6π+24
C.12π+12
D.24π+12
【考点】由三视图求面积、体积.
【分析】由三视图可知几何体为半圆柱与直三棱柱的组合体,利用体积公式,即可得出结论.
【解答】解:由三视图可知几何体为半圆柱与直三棱柱的组合体,
V==6π+12,
故选A.
7.甲、乙两名选手参加歌手
( http: / / www.21cnjy.com )大赛时,5名评委打的分数,用茎叶图表示(如图)s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是(填“>”、“<”或“=”)( )
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
【考点】茎叶图;极差、方差与标准差.
【分析】首先做出两个选手
( http: / / www.21cnjy.com )的平均分,结果两个选手的平均分相同,观察两个人的分数在茎叶图中甲的分数是单峰的,比较集中,而乙的分数是双峰的,比较分散,由茎叶图的性质可得答案.
【解答】解:甲选手的平均分是=84
乙选手的平均分是=84
这两个选手的平均分是相同的,
从茎叶图上看甲的分数是单峰的,分数比较集中,
乙的分数是双峰的,分数分散,
∴甲的方差一定小于乙的方差,
故选C.
8.已知直线l1:(k﹣3)x+(4﹣k)y+1=0与l2:2(k﹣3)x﹣2y+3=0平行,则k的值是( )
A.1或3
B.1或5
C.3或5
D.1或2
【考点】直线的一般式方程与直线的平行关系.
【分析】当k﹣3=0时,求出两直线的方程,检验是否平行;当k﹣3≠0时,由一次项系数之比相等且不等于常数项之比,求出k的值.
【解答】解:由两直线平行得,当k﹣3=0时,两直线的方程分别为
y=﹣1
和
y=,显然两直线平行.
当k﹣3≠0时,由
=≠,可得
k=5.综上,k的值是
3或5,
故选
C.
9.为了了解某校九年级1600名学生的
( http: / / www.21cnjy.com )体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
【考点】频率分布直方图.
【分析】根据频率=小矩形的高×组距,求得第一组,第二组,第三组的频率,利用中位数的左,右两边频率相等求得中位数;验证A是否正确.
根据最高矩形的底边中点的横坐标为数据的众数求得众数;验证B是否正确;
利用频率=小矩形的高×组距=求1分钟仰卧起坐的成绩超过30次的频数和1分钟仰卧起坐的成绩少于20次的频数,由此可验证C、D是否正确.
【解答】解:第一组数据的频率为0.02×5=0.1;第二组数据的频率为0.06×5=0.3,第三组的频率为0.08×5=0.4,
∴中位数在第三组内,设中位数为25+x
( http: / / www.21cnjy.com ),则x×0.08=0.5﹣0.1﹣0.3=0.1,∴x=1.25,∴数据的中位数为26.25,故A正确;
最高矩形是第三组数据,第三组数据的中间值为27.5,∴众数为27.5,故B正确;
学生1分钟仰卧起坐的成绩超过30次的频率为0.04×5=0.2,∴超过30次的人数为1600×0.2=320人,故C正确;
学生1分钟仰卧起坐的成绩少于20次
( http: / / www.21cnjy.com )的频率为0.02×5=0.1,∴1分钟仰卧起坐的成绩少于20次的人数为1600×0.1=160人,故D错误.
故选:D.
10.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( )
A.
B.
C.2
D.
【考点】直线和圆的方程的应用.
【分析】先根据点到直线的距离公式求出圆心
( http: / / www.21cnjy.com )到弦的距离即弦心距OD,然后根据垂径定理得到垂足为弦长的中点D,根据勾股定理求出弦长的一半BD,乘以2即可求出弦长AB.
【解答】解:连接OB,过O作OD⊥AB,根据垂径定理得:D为AB的中点,
根据(x+2)2+(y﹣2)2=2得到圆心坐标为(﹣2,2),半径为.
圆心O到直线AB的距离OD==,而半径OB=,
则在直角三角形OBD中根据勾股定理得BD==,所以AB=2BD=
故选D.
11.给出一个如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是( )
A.1
B.2
C.3
D.4
【考点】选择结构.
【分析】由已知的流程图,我们易得这是
( http: / / www.21cnjy.com )一个计算并输出分段函数函数值的程序,我们根据条件,分x≤2,2<x≤5,x>5三种情况分别讨论,满足输入的x值与输出的y值相等的情况,即可得到答案.
【解答】解:当x≤2时,由x2=x得:x=0,1满足条件;
当2<x≤5时,由2x﹣3=x得:x=3,满足条件;
当x>5时,由=x得:x=±1,不满足条件,
故这样的x值有3个.
故选C.
12.已知点P(x,y)是直线kx+y
( http: / / www.21cnjy.com )+4=0(k>0)上一动点,PA,PB是圆C:x2+y2﹣2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为( )
A.3
B.
C.
D.2
【考点】直线和圆的方程的应用.
【分析】先求圆的半径,四边形P
( http: / / www.21cnjy.com )ACB的最小面积是2,转化为三角形PBC的面积是1,求出切线长,再求PC的距离也就是圆心到直线的距离,可解k的值.
【解答】解:圆C:x2+y2﹣2y=0的圆心(0,1),半径是r=1,
由圆的性质知:S四边形PACB=2S△PBC,四边形PACB的最小面积是2,
∴S△PBC的最小值=1=rd(d是切线长)∴d最小值=2
圆心到直线的距离就是PC的最小值,
∵k>0,∴k=2
故选D.
二、填空题(每小题5分,4小题共20分)
13.在△ABC中,A=75°,C=60°,c=1,则边b的长为 .
【考点】余弦定理.
【分析】由已知及三角形内角和定理可求B的值,进而利用正弦定理可求b的值.
【解答】解:∵A=75°,C=60°,c=1,
∴B=180°﹣A﹣C=45°,
∴由正弦定理可得:b===.
故答案为:.
14.在[0,10]上随机的取一个数m,则事件“圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2相交”发生的概率 .
【考点】几何概型.
【分析】计算两圆的圆心距d,利用两圆相交R﹣r<d<R+r,求出m的取值范围,再利用几何概型计算对应的概率值.
【解答】解:圆x2+y2=4与圆(x﹣3)2+(y﹣4)2=m2的圆心距为
d==5,
若两圆相交,则,
解得3<m<7;
所以,两圆相交时发生的概率为:
P==.
故答案为:.
15.已知实数x,y满足,则z=2x﹣3y的最小值是 ﹣6 .
【考点】简单线性规划.
【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,分类代入目标函数求解.
【解答】解:由约束条件作出可行域如图,
联立,解得A(3,4).
化目标函数z=2x﹣3y为.
由图可知,当直线过A时,直线在y轴上的截距最大,z有最小值为2×3﹣3×4=﹣6.
故答案为:﹣6.
16.已知圆C的方程为x2+y2+8x
( http: / / www.21cnjy.com )+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围为 .
【考点】圆的一般方程.
【分析】将圆C的方程整理为标准形式,找出圆
( http: / / www.21cnjy.com )心C的坐标与半径r,根据直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,即圆心到直线y=kx﹣2的距离小于等于2,利用点到直线的距离公式列出关于k的不等式求出不等式的解集即可得到k的范围.
【解答】解:将圆C的方程整理为标准方程得:(x+4)2+y2=1,
∴圆心C(﹣4,0),半径r=1,
∵直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴圆心(﹣4,0)到直线y=kx﹣2的距离d=,
解得:≤k≤0.
故答案为:.
三、解答题(第17题10分,其余每题12分,共70分,解答应写出证明过程或演算步骤)
17.某市有M,N,S三所高
( http: / / www.21cnjy.com )校,其学生会学习部有“干事”人数分别为36,24,12,现采用分层抽样的方法从这些“干事”中抽取6名进行“大学生学习部活动现状”调查.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
【考点】古典概型及其概率计算公式;分层抽样方法.
【分析】(Ⅰ)求出抽样比,即可从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)在抽取到的6名干事中,来自高校M
( http: / / www.21cnjy.com )的3名分别记为1、2、3,来自高校N的2名分别记为a、b,来自高校S的1名记为c,写出选出2名干事的所有可能结果,设A={所选2名干事来自同一高校},写出事件A的所有可能结果,利用古典概型求解即可.
【解答】解:(Ⅰ)抽样比为:,
故应从M,N,S这三所高校抽取的“干事”人数分别为3,2,1;
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,
来自高校N的2名分别记为a、b,来自高校S的1名记为c,
则选出2名干事的所有可能结果为:
{1,2},{1,3},{1,a
},{1,b
},{1,c},
{2,3},{2,a},{2,b},{2,c},
{3,a},{3,b
},{3,c
},
{
a,b
},{
a,c
},
{
b,c}共15种.
设A={所选2名干事来自同一高校},
事件A的所有可能结果为{1,2},{1,3},{2,3},{a,b},共4种,
所以.
18.下表是关于某设备的使用年限(年)和所需要的维修费用y(万元)的几组统计数据:
x
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
)
(参考公式:
=;;)
【考点】线性回归方程.
【分析】(1)由题意易得散点图:
(2)由已知数据求出=4,
=5,
=90,结合参考数据可得和,可得回归直线方程;
(3)把x=10代入(2)中的方程计算可得;
【解答】解:(1)由题意可得散点图如图:
(2)从散点图可知,变量y与x之间有较强的线性相关性.
由已知数据有:
=4,
=5,
=90,
又由参考数据知
∴===1.23,
∴=﹣=5﹣1.23×4=0.08,
∴回归直线方程为=1.23x+0.08;
(3)当x=10时,维修费用=1.23×10+0.08=12.38(万元)
19.已知正方形ABCD的边长为1,如图所示:
(1)在正方形内任取一点,求事件“|AM|≤1”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形BAD内,请据此估计圆周率π的近似值(精确到0.001).
【考点】模拟方法估计概率.
【分析】(1)根据已知条件,求出满足条
( http: / / www.21cnjy.com )件的正方形ABCD的面积,及事件“|AM|≤1”对应平面区域的面积,代入几何概型计算公式,即可求出答案.
(2)正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内,频率为,用频率估计概率,由(1)知,可得圆周率π的近似值.
【解答】解:(1)如图,在边长为1的正方
( http: / / www.21cnjy.com )形ABCD内任取一点M,满足条件的点M落在扇形BAD内(图中阴影部分),由几何概型概率计算公式,有:,
故事件“|AM|≤1”发生的概率为.
(2)正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内,频率为,
用频率估计概率,由(1)知,
∴,即π的近似值为3.143.
20.设△ABC的内角A,B,C所对应的边长分别是a,b,c且cosB=,b=2
(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
【考点】余弦定理;正弦定理.
【分析】(Ⅰ)由cosB=,B∈(0,π),可得sinB=,再利用正弦定理即可得出.
(Ⅱ)由S△ABC==3,可得ac=.再利用余弦定理即可得出.
【解答】解:(Ⅰ)∵cosB=,B∈(0,π),
∴sinB==,
由正弦定理可知:,
∴a=.
(Ⅱ)∵S△ABC===3,
∴ac=.
由余弦定理得:b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣2ac×=4,
∴(a+c)2=+4=28,
故:a+c=2.
21.设函数.
(1)写出函数f(x)的最小正周期及单调递减区间;
(2)当时,函数f(x)的最大值与最小值的和为,求a的值.
【考点】三角函数的恒等变换及化简求值;三角函数的周期性及其求法;正弦函数的定义域和值域;正弦函数的单调性.
【分析】(1)根据二倍角公式,和辅助角公式,我们易将函数的解析化简为正弦型函数的形式,进而求出函数f(x)的最小正周期及单调递减区间;
(2)当时,根据函数f(x)的最大值与最小值的和为,我们可构造出关于a的方程,解方程即可得到a的值.
【解答】解(1),
∴T=π.
.
故函数f(x)的单调递减区间是.
(2)∵,∴.∴.
当时,原函数的最大值与最小值的和=,∴a=0
22.已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
【考点】等差数列与等比数列的综合.
【分析】(I)将已知等式用等差数列{an}的首项、公差表示,列出方程组,求出首项、公差;利用等差数列的通项公式求出数列{an}的通项公式.
(II)利用等比数列的通项公式求出,进一步求出bn,根据数列{bn}通项的特点,选择错位相减法求出数列{bn}的前n项和Tn.
【解答】解:(Ⅰ)依题意得
解得,
∴an=a1+(n﹣1)d=3+2(n﹣1)=2n+1,
即an=2n+1.
(Ⅱ),
bn=an 3n﹣1=(2n+1) 3n﹣1
Tn=3+5 3+7 32+…+(2n+1) 3n﹣1
3Tn=3 3+5 32+7 33+…+(2n﹣1) 3n﹣1+(2n+1) 3n
﹣2Tn=3+2 3+2 32+…+2 3n﹣1﹣(2n+1)3n
∴Tn=n 3n.
2017年3月8日
