云南省保山市腾冲八中2016-2017学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 云南省保山市腾冲八中2016-2017学年高二(上)期末数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 15:34:48 | ||
图片预览




文档简介
2016-2017学年云南省保山市腾冲八中高二(上)期末数学试卷(文科)
一、选择题(12×5=60)
1.设集合A={1,2,3,4},B={x|x2≤4},则A∩B=( )
A.{1,2}
B.{0,1}
C.{0,1,2}
D.{1,2,3,4}
2.“a>b”是“2a>2b”的_________条件.( )
A.充分不必要
B.必要不充分
C.充要
D.既不充分也不必要
3.已知向量=(2,1),=(1,m),且∥,则m等于( )
A.2
B.
C.﹣2
D.
4.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=( )
A.2
B.1
C.0
D.﹣2
5.△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2,则b等于( )
A.
B.2
C.2
D.4
6.命题“若a>b,则2a>2b﹣1”的否命题为( )
A.若a>b,则有2a≤2b﹣1
B.若a≤b,则有2a≤2b﹣1
C.若a≤b,则有2a>2b﹣1
D.若2a≤2b﹣1,则有a≤b
7.如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
A.5π
B.6π
C.7π
D.8π
8.焦点在x轴上的双曲线的两条渐进线方程为:,则该双曲线的离心率e=( )
A.
B.
C.
D.
9.若x,y满足约束条件,则的最大值为( )
A.1
B.2
C.3
D.
10.已知变量x,y有如下观察数据
x
0
1
3
4
y
2.4
4.5
4.6
6.5
若y对x的回归方程是=0.83x+a则a=( )
A.2.4
B.2.84
C.3.67
D.3.95
11.椭圆(a>b>0)的左、右顶点分
( http: / / www.21cnjy.com )别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A.
B.
C.
D.
12.双曲线的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
A.12
B.16
C.20
D.24
二、填空题(5×4=20)
13.等差数列{an}中,若a3+a5+a7=15,则S9= .
14.已知抛物线y2=4x,P是抛物线上一点,F为焦点,若|PF|=5,则点P的坐标是 .
15.焦点在x轴上,焦距等于4,且经过点的椭圆标准方程是 .
16.数列{an}满足,且a1=1,则通项公式an= .
三、解答题(写出必要的文字说明,演算步骤,证明过程)
17.在等比数列{an}中,.
(1)求数列{an}的通项公式;
(2)若分别为等差数列{bn}的第4项和第16项,求数列{bn}的前n项和Sn.
18.现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
19.在四棱锥P﹣ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
(1)证明PA∥面EDB;
(2)求异面直线PC与AD能成角的大小.
20.在△ABC中,角A,B,C的对边分别为.
(Ⅰ)求cosB的值;
(Ⅱ)若,求a和c的值.
21.某工厂生产某种零件,每个零件成本为4
( http: / / www.21cnjy.com )0元,出厂单价为70元.该厂为了鼓励销售商订购,决定当一次订购量超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不能低于61元.
(1)设订购量为x个时,零件的实际出厂单价为y元,写出函数y=f(x)的函数解析式;
(2)当销售商一次订购500个时,该厂获得的利润是多少元?
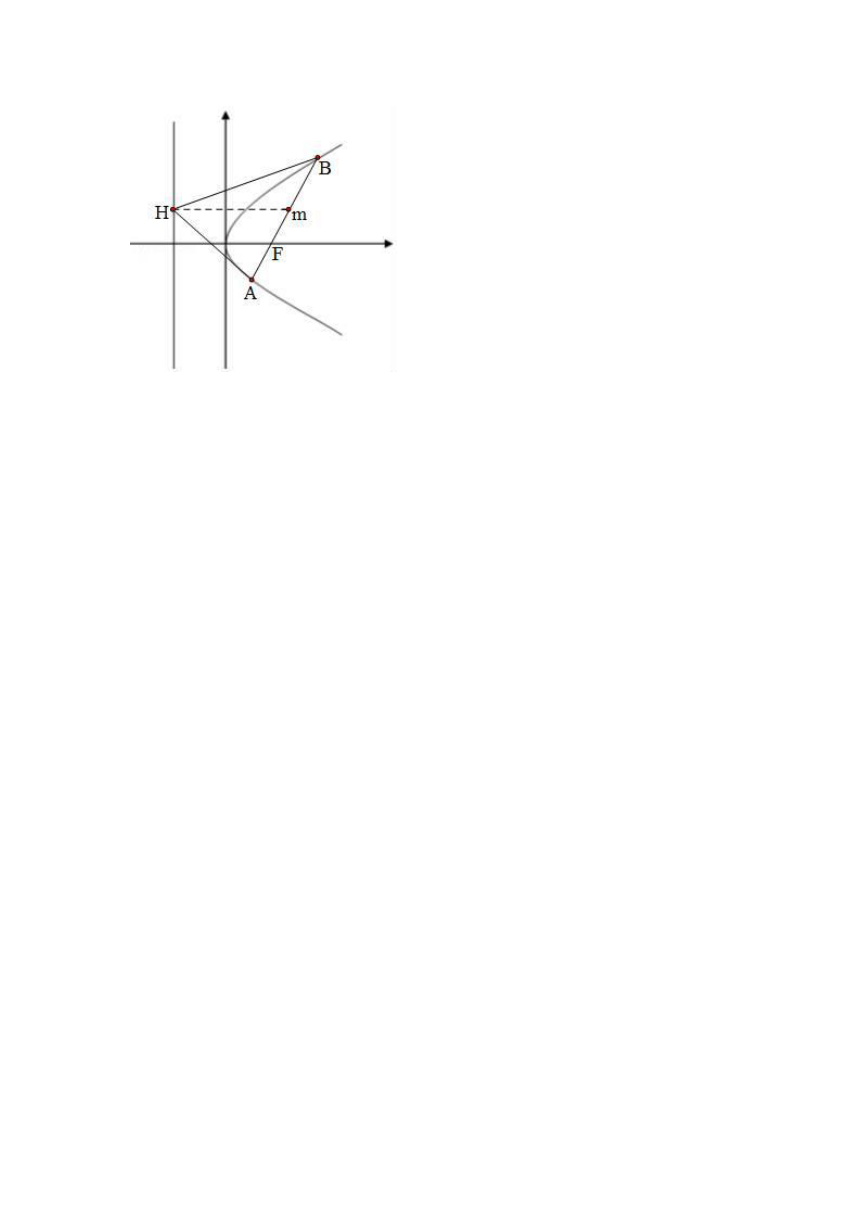
22.抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
(1)求弦AB的长;
(2)若MH垂直于准线,垂足为H.求∠AHB的度数.
2016-2017学年云南省保山市腾冲八中高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(12×5=60)
1.设集合A={1,2,3,4},B={x|x2≤4},则A∩B=( )
A.{1,2}
B.{0,1}
C.{0,1,2}
D.{1,2,3,4}
【考点】交集及其运算.
【分析】求出B中x的范围确定出B,找出A与B的交集即可.
【解答】解:由B中不等式变形得:(x+2)(x﹣2)≤0,
解得:﹣2≤x≤2,即B=[﹣2,2],
∵A={1,2,3,4},
∴A∩B={1,2},
故选:A.
2.“a>b”是“2a>2b”的_________条件.( )
A.充分不必要
B.必要不充分
C.充要
D.既不充分也不必要
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用指数函数的单调性、充要条件的判定方法即可得出.
【解答】解:“a>b” “2a>2b”,
∴“a>b”是“2a>2b”的充要条件.
故选:C.
3.已知向量=(2,1),=(1,m),且∥,则m等于( )
A.2
B.
C.﹣2
D.
【考点】平面向量共线(平行)的坐标表示.
【分析】利用向量共线定理即可得出.
【解答】解:∵∥,
∴2m﹣1=0,
解得m=.
故选:B.
4.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=( )
A.2
B.1
C.0
D.﹣2
【考点】函数奇偶性的性质;函数的值.
【分析】由条件利用函数的奇偶性和单调性的性质可得
f(﹣1)=﹣f(1),运算求得结果.
【解答】解:∵已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=﹣f(1)=﹣(1+1)=﹣2,
故选D.
5.△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2,则b等于( )
A.
B.2
C.2
D.4
【考点】正弦定理.
【分析】由内角和定理求出C,再由正弦定理,得到b=,代入数据,即可得到b.
【解答】解:∵A=75°,B=45°,∴C=180°﹣A﹣B=60°,
由正弦定理得,
=,
得到b==
=2.
故选:B.
6.命题“若a>b,则2a>2b﹣1”的否命题为( )
A.若a>b,则有2a≤2b﹣1
B.若a≤b,则有2a≤2b﹣1
C.若a≤b,则有2a>2b﹣1
D.若2a≤2b﹣1,则有a≤b
【考点】四种命题间的逆否关系.
【分析】否命题是:否定命题的条件的同时否定命题的结论.
【解答】解:根据否命题的定义,
命题的否命题是:若a≤b,则2a≤2b﹣1,
故选:B.
7.如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
A.5π
B.6π
C.7π
D.8π
【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.
【分析】由已知中的三视图,可得该几何体是一个半球与圆柱的组合体,其表面由一个半球面,一个圆柱的底面和侧面构成,进而得到答案.
【解答】解:由已知中的三视图,可得该几何体是一个半球与圆柱的组合体,
其表面由一个半球面,一个圆柱的底面和侧面构成,
故表面积S=π 12+π 12+2π 2=7π,
故选:C
8.焦点在x轴上的双曲线的两条渐进线方程为:,则该双曲线的离心率e=( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】由题意可得=,再由双曲线的离心率为
e=,运算求得结果.
【解答】解:根据焦点在x轴上的双曲线的渐近线方程是:,可得=,
则该双曲线的离心率为
e==,
故选A.
9.若x,y满足约束条件,则的最大值为( )
A.1
B.2
C.3
D.
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值.
【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).
设k=,则k的几何意义为区域内的点到原点的斜率,
由图象知OA的斜率最大,
由,解得,即A(1,3),
则kOA==3,
即的最大值为3.
故选:C.
10.已知变量x,y有如下观察数据
x
0
1
3
4
y
2.4
4.5
4.6
6.5
若y对x的回归方程是=0.83x+a则a=( )
A.2.4
B.2.84
C.3.67
D.3.95
【考点】线性回归方程.
【分析】根据已知表中数据,可计算出数据中心点的坐标,根据数据中心点一定在回归直线上,代入回归直线方程=0.83x+a,解方程可得a的值.
【解答】解:由已知中的数据可得:
=(0+1+3+4)÷4=2,
=(2.4+4.5+4.6+6.5)÷4=4.5,
∵数据中心点(2,4.5)一定在回归直线上,
∴4.5=0.83×2+a
解得a=2.84,
故选:B.
11.椭圆(a>b>0)的左、右顶点分别
( http: / / www.21cnjy.com )是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A.
B.
C.
D.
【考点】椭圆的简单性质;等比关系的确定.
【分析】由题意可得,|AF
( http: / / www.21cnjy.com )1|=a﹣c,|F1F2|=2c,|F1B|=a+c,由|AF1|,|F1F2|,|F1B|成等比数列可得到e2==,从而得到答案.
【解答】解:设该椭圆的半焦距为c,由题意可得,|AF1|=a﹣c,|F1F2|=2c,|F1B|=a+c,
∵|AF1|,|F1F2|,|F1B|成等比数列,
∴(2c)2=(a﹣c)(a+c),
∴=,即e2=,
∴e=,即此椭圆的离心率为.
故选B.
12.双曲线的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
A.12
B.16
C.20
D.24
【考点】双曲线的简单性质.
【分析】求得双曲线的a,b,c,设|P
( http: / / www.21cnjy.com )F1|=m,|PF2|=n,由双曲线的定义,可得|m﹣n|=6,运用勾股定理,由S=mn,即可求得△F1PF2的面积.
【解答】解:由题意可得双曲线的a=3,b=4,c=5,
左右焦点分别为F1(﹣5,0),F2(5,0),
设|PF1|=m,|PF2|=n,
由双曲线的定义可得|m﹣n|=6,
∠F1PF2=90°,
由勾股定理可得
100=m2+n2=(m﹣n)2+2mn=62+2mn,
∴mn=32.
则△F1PF2的面积S=mn=×32=16.
故选:B.
二、填空题(5×4=20)
13.等差数列{an}中,若a3+a5+a7=15,则S9= 45 .
【考点】等差数列的通项公式.
【分析】由已知结合等差数列的性质求得a5,再由等差数列的前n项和求得答案.
【解答】解:在等差数列{an}中,由a3+a5+a7=15,得3a5=15,∴a5=5.
则.
故答案为:45.
14.已知抛物线y2=4x,P是抛物线上一点,F为焦点,若|PF|=5,则点P的坐标是 (4,4)或(4,﹣4) .
【考点】抛物线的简单性质.
【分析】先设出该点的坐标,根据抛物
( http: / / www.21cnjy.com )线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得x的值,代入抛物线方程求得y.
【解答】解:设该点坐标为(x,y)
根据抛物线定义可知x+1=5,解得x=4,代入抛物线方程求得y=±4
故这点点坐标为:(4,4)或(4,﹣4)
故答案为:(4,4)或(4,﹣4).
15.焦点在x轴上,焦距等于4,且经过点的椭圆标准方程是 .
【考点】椭圆的标准方程.
【分析】设椭圆的方程为(a>b>0),根据题意建立关于a、b的方程组,解出a2、b2的值,即可得到所求椭圆标准方程.
【解答】解:由椭圆的焦点在x轴上,设椭圆的方程为(a>b>0)
∵焦距等于4,且椭圆经过点.
∴,解之得a2=36,b2=32(舍负)
因此,椭圆的标准方程为.
故答案为:
16.数列{an}满足,且a1=1,则通项公式an= 2n﹣1 .
【考点】数列递推式.
【分析】数列{an}满足,化为=2,且a1=1,利用等比数列的通项公式即可得出.
【解答】解:数列{an}满足,
∴=2,且a1=1,
则数列{an}是等比数列,公比为2,首项为1.
则通项公式an=2n﹣1.
故答案为:2n﹣1.
三、解答题(写出必要的文字说明,演算步骤,证明过程)
17.在等比数列{an}中,.
(1)求数列{an}的通项公式;
(2)若分别为等差数列{bn}的第4项和第16项,求数列{bn}的前n项和Sn.
【考点】数列的求和;等比数列的通项公式.
【分析】(1)设等比数列{an}的公比为q,由.可得,解出即可得出.
(2)b4=a3=8,b16=a5=32,可得,解得b1,d.利用求和公式即可得出.
【解答】解:(1)设等比数列{an}的公比为q,∵.∴,解得a1=q=2.∴an=2n.
(2)b4=a3=8,b16=a5=32,∴,解得b1=d=2.
∴Sn=2n+=n2+n.
18.现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
【考点】古典概型及其概率计算公式;列举法计算基本事件数及事件发生的概率.
【分析】(1)根据题意,设事件A为“都是甲类题”,由组合数原理,可得试验结果总数与A包含的基本事件数目,由古典概率公式计算可得答案,
(2)设事件B为“所取的2道题不是
( http: / / www.21cnjy.com )同一类题”,分析可得是组合问题,由组合公式,可得从6件中抽取2道的情况数目与抽出的2道是一个甲类题,一个乙类题的情况数目,由古典概率公式计算可得答案.
【解答】解:(1)从中任取2道题解答,试验结果有=15种;
设事件A为“所取的2道题都是甲类题”,则包含的基本事件共有C=6种,
因此,P(A)=.
(2)设事件B为“所取的2道题不是同一类题”,
从6件中抽取2道,有C62种情况,
而抽出的2道是一个甲类题,一个乙类题的情况数目,有C41 C21=8种情况,
根据古典概型的计算,有P(B)=.
19.在四棱锥P﹣ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
(1)证明PA∥面EDB;
(2)求异面直线PC与AD能成角的大小.
【考点】异面直线及其所成的角;直线与平面平行的判定.
【分析】(1)连接AC交BD于O,连接OE,证明OE∥PA,即可证明PA∥平面EDB;
(2)证明AD⊥平面PCD,即可证明AD⊥PC,可得异面直线PC与AD所成角的大小.
【解答】证明:(1)连接AC交BD于O,连接OE
∵底面ABCD是正方形,∴O为AC中点,
∵在△PAC中,E是PC的中点,
∴OE∥PA,…
∵OE 平面EDB,PA 平面EDB,
∴PA∥平面EDB.…
(2)∵侧棱PD⊥底面ABCD,AD 底面ABCD,
∴PD⊥AD,
∵底面ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,
∴AD⊥平面PCD.…
∴AD⊥PC,
∴异面直线PC与AD所成角为90°.…
20.在△ABC中,角A,B,C的对边分别为.
(Ⅰ)求cosB的值;
(Ⅱ)若,求a和c的值.
【考点】余弦定理;同角三角函数基本关系的运用.
【分析】(1)利用诱导公式求出sin的值,从而利用二倍角的余弦公式求得cosB.
(2)由两个向量的数量积的定义求出ac的值,再利用余弦定理求出a和c的值.
【解答】解:(1)∵cos=,
∴sin=sin(﹣)=,
∴cosB=1﹣2sin2=.
(2)由 =2可得
a c cosB=2,又cosB=,
故ac=6,
由
b2=a2+c2﹣2accosB
可得a2+c2=12,
∴(a﹣c)2=0,
故
a=c,
∴a=c=.
21.某工厂生产某种零件,每个零件成本为40
( http: / / www.21cnjy.com )元,出厂单价为70元.该厂为了鼓励销售商订购,决定当一次订购量超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不能低于61元.
(1)设订购量为x个时,零件的实际出厂单价为y元,写出函数y=f(x)的函数解析式;
(2)当销售商一次订购500个时,该厂获得的利润是多少元?
【考点】分段函数的应用.
【分析】(1)由题意设每个
( http: / / www.21cnjy.com )零件的实际出厂价恰好降为61元时,一次订购量为x0个,则x0=100+,因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为61元;前100件单价为y,当进货件数大于等于550件时,y=61,则当100<x<550时,y=70﹣0.02(x﹣100),得到y为分段函数,写出解析式即可;
(2)设销售商的一次订购量为x个时,工厂获得的利润为L元,表示出L与x的函数关系式,然后令x=500,即可得到对应的利润.
【解答】解:(1)设每个零件的实际出厂价恰好降为61元时,一次订购量为x0个,则x0=100+=550,
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为61元.
当0<x≤100时,y=70;
当100<x<550时,y=70﹣0.02(x﹣100)=72﹣0.02x;
当x≥550时,y=61.
所以y=f(x)=;
(2)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(y﹣40)x=,
当x=500时,L=32×500﹣0.02×5002=11000,
因此,当销售商一次订购500个零件时,该厂获得的利润是11000元.
22.抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
(1)求弦AB的长;
(2)若MH垂直于准线,垂足为H.求∠AHB的度数.
【考点】抛物线的简单性质.
【分析】(1)根据抛物线
( http: / / www.21cnjy.com )方程求得抛物线的焦点坐标,进而根据点斜式求得直线的方程与抛物线方程联立,消去y,根据韦达定理求得x1+x2=的值,进而根据抛物线的定义可知|AB|=x1++x2+=x1+x2+p,求得答案.
(2)过A,B做准线的垂线,垂足分别为
( http: / / www.21cnjy.com )P,Q,则|AP|=|AF|,|BQ|=|BF|,得出以AB为直径的圆M与准线相切于H,即可得出结论.
【解答】解:(1)抛物线焦点为(1,0),且斜率为1,
则直线方程为y=x﹣1,代入抛物线方程y2=4x得
x2﹣6x+1=0,设A(x1,y1),B(x2,y2)
∴x1+x2=6
根据抛物线的定义可知|AB|=x1++x2+=x1+x2+p=6+2=8;
(2)过A,B做准线的垂线,垂足分别为P,Q,则|AP|=|AF|,|BQ|=|BF|,
∴|AB|=|AF|+|BF|=|AP|+|BQ|,
∵M是AB的中点,
∴|MH|==4,
∴以AB为直径的圆M与准线相切于H,
∴∠AHB=90°.
2017年3月8日
一、选择题(12×5=60)
1.设集合A={1,2,3,4},B={x|x2≤4},则A∩B=( )
A.{1,2}
B.{0,1}
C.{0,1,2}
D.{1,2,3,4}
2.“a>b”是“2a>2b”的_________条件.( )
A.充分不必要
B.必要不充分
C.充要
D.既不充分也不必要
3.已知向量=(2,1),=(1,m),且∥,则m等于( )
A.2
B.
C.﹣2
D.
4.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=( )
A.2
B.1
C.0
D.﹣2
5.△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2,则b等于( )
A.
B.2
C.2
D.4
6.命题“若a>b,则2a>2b﹣1”的否命题为( )
A.若a>b,则有2a≤2b﹣1
B.若a≤b,则有2a≤2b﹣1
C.若a≤b,则有2a>2b﹣1
D.若2a≤2b﹣1,则有a≤b
7.如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
A.5π
B.6π
C.7π
D.8π
8.焦点在x轴上的双曲线的两条渐进线方程为:,则该双曲线的离心率e=( )
A.
B.
C.
D.
9.若x,y满足约束条件,则的最大值为( )
A.1
B.2
C.3
D.
10.已知变量x,y有如下观察数据
x
0
1
3
4
y
2.4
4.5
4.6
6.5
若y对x的回归方程是=0.83x+a则a=( )
A.2.4
B.2.84
C.3.67
D.3.95
11.椭圆(a>b>0)的左、右顶点分
( http: / / www.21cnjy.com )别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A.
B.
C.
D.
12.双曲线的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
A.12
B.16
C.20
D.24
二、填空题(5×4=20)
13.等差数列{an}中,若a3+a5+a7=15,则S9= .
14.已知抛物线y2=4x,P是抛物线上一点,F为焦点,若|PF|=5,则点P的坐标是 .
15.焦点在x轴上,焦距等于4,且经过点的椭圆标准方程是 .
16.数列{an}满足,且a1=1,则通项公式an= .
三、解答题(写出必要的文字说明,演算步骤,证明过程)
17.在等比数列{an}中,.
(1)求数列{an}的通项公式;
(2)若分别为等差数列{bn}的第4项和第16项,求数列{bn}的前n项和Sn.
18.现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
19.在四棱锥P﹣ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
(1)证明PA∥面EDB;
(2)求异面直线PC与AD能成角的大小.
20.在△ABC中,角A,B,C的对边分别为.
(Ⅰ)求cosB的值;
(Ⅱ)若,求a和c的值.
21.某工厂生产某种零件,每个零件成本为4
( http: / / www.21cnjy.com )0元,出厂单价为70元.该厂为了鼓励销售商订购,决定当一次订购量超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不能低于61元.
(1)设订购量为x个时,零件的实际出厂单价为y元,写出函数y=f(x)的函数解析式;
(2)当销售商一次订购500个时,该厂获得的利润是多少元?
22.抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
(1)求弦AB的长;
(2)若MH垂直于准线,垂足为H.求∠AHB的度数.
2016-2017学年云南省保山市腾冲八中高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(12×5=60)
1.设集合A={1,2,3,4},B={x|x2≤4},则A∩B=( )
A.{1,2}
B.{0,1}
C.{0,1,2}
D.{1,2,3,4}
【考点】交集及其运算.
【分析】求出B中x的范围确定出B,找出A与B的交集即可.
【解答】解:由B中不等式变形得:(x+2)(x﹣2)≤0,
解得:﹣2≤x≤2,即B=[﹣2,2],
∵A={1,2,3,4},
∴A∩B={1,2},
故选:A.
2.“a>b”是“2a>2b”的_________条件.( )
A.充分不必要
B.必要不充分
C.充要
D.既不充分也不必要
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用指数函数的单调性、充要条件的判定方法即可得出.
【解答】解:“a>b” “2a>2b”,
∴“a>b”是“2a>2b”的充要条件.
故选:C.
3.已知向量=(2,1),=(1,m),且∥,则m等于( )
A.2
B.
C.﹣2
D.
【考点】平面向量共线(平行)的坐标表示.
【分析】利用向量共线定理即可得出.
【解答】解:∵∥,
∴2m﹣1=0,
解得m=.
故选:B.
4.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=( )
A.2
B.1
C.0
D.﹣2
【考点】函数奇偶性的性质;函数的值.
【分析】由条件利用函数的奇偶性和单调性的性质可得
f(﹣1)=﹣f(1),运算求得结果.
【解答】解:∵已知函数f(x)为奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=﹣f(1)=﹣(1+1)=﹣2,
故选D.
5.△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2,则b等于( )
A.
B.2
C.2
D.4
【考点】正弦定理.
【分析】由内角和定理求出C,再由正弦定理,得到b=,代入数据,即可得到b.
【解答】解:∵A=75°,B=45°,∴C=180°﹣A﹣B=60°,
由正弦定理得,
=,
得到b==
=2.
故选:B.
6.命题“若a>b,则2a>2b﹣1”的否命题为( )
A.若a>b,则有2a≤2b﹣1
B.若a≤b,则有2a≤2b﹣1
C.若a≤b,则有2a>2b﹣1
D.若2a≤2b﹣1,则有a≤b
【考点】四种命题间的逆否关系.
【分析】否命题是:否定命题的条件的同时否定命题的结论.
【解答】解:根据否命题的定义,
命题的否命题是:若a≤b,则2a≤2b﹣1,
故选:B.
7.如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
A.5π
B.6π
C.7π
D.8π
【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.
【分析】由已知中的三视图,可得该几何体是一个半球与圆柱的组合体,其表面由一个半球面,一个圆柱的底面和侧面构成,进而得到答案.
【解答】解:由已知中的三视图,可得该几何体是一个半球与圆柱的组合体,
其表面由一个半球面,一个圆柱的底面和侧面构成,
故表面积S=π 12+π 12+2π 2=7π,
故选:C
8.焦点在x轴上的双曲线的两条渐进线方程为:,则该双曲线的离心率e=( )
A.
B.
C.
D.
【考点】双曲线的简单性质.
【分析】由题意可得=,再由双曲线的离心率为
e=,运算求得结果.
【解答】解:根据焦点在x轴上的双曲线的渐近线方程是:,可得=,
则该双曲线的离心率为
e==,
故选A.
9.若x,y满足约束条件,则的最大值为( )
A.1
B.2
C.3
D.
【考点】简单线性规划.
【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值.
【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).
设k=,则k的几何意义为区域内的点到原点的斜率,
由图象知OA的斜率最大,
由,解得,即A(1,3),
则kOA==3,
即的最大值为3.
故选:C.
10.已知变量x,y有如下观察数据
x
0
1
3
4
y
2.4
4.5
4.6
6.5
若y对x的回归方程是=0.83x+a则a=( )
A.2.4
B.2.84
C.3.67
D.3.95
【考点】线性回归方程.
【分析】根据已知表中数据,可计算出数据中心点的坐标,根据数据中心点一定在回归直线上,代入回归直线方程=0.83x+a,解方程可得a的值.
【解答】解:由已知中的数据可得:
=(0+1+3+4)÷4=2,
=(2.4+4.5+4.6+6.5)÷4=4.5,
∵数据中心点(2,4.5)一定在回归直线上,
∴4.5=0.83×2+a
解得a=2.84,
故选:B.
11.椭圆(a>b>0)的左、右顶点分别
( http: / / www.21cnjy.com )是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为( )
A.
B.
C.
D.
【考点】椭圆的简单性质;等比关系的确定.
【分析】由题意可得,|AF
( http: / / www.21cnjy.com )1|=a﹣c,|F1F2|=2c,|F1B|=a+c,由|AF1|,|F1F2|,|F1B|成等比数列可得到e2==,从而得到答案.
【解答】解:设该椭圆的半焦距为c,由题意可得,|AF1|=a﹣c,|F1F2|=2c,|F1B|=a+c,
∵|AF1|,|F1F2|,|F1B|成等比数列,
∴(2c)2=(a﹣c)(a+c),
∴=,即e2=,
∴e=,即此椭圆的离心率为.
故选B.
12.双曲线的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
A.12
B.16
C.20
D.24
【考点】双曲线的简单性质.
【分析】求得双曲线的a,b,c,设|P
( http: / / www.21cnjy.com )F1|=m,|PF2|=n,由双曲线的定义,可得|m﹣n|=6,运用勾股定理,由S=mn,即可求得△F1PF2的面积.
【解答】解:由题意可得双曲线的a=3,b=4,c=5,
左右焦点分别为F1(﹣5,0),F2(5,0),
设|PF1|=m,|PF2|=n,
由双曲线的定义可得|m﹣n|=6,
∠F1PF2=90°,
由勾股定理可得
100=m2+n2=(m﹣n)2+2mn=62+2mn,
∴mn=32.
则△F1PF2的面积S=mn=×32=16.
故选:B.
二、填空题(5×4=20)
13.等差数列{an}中,若a3+a5+a7=15,则S9= 45 .
【考点】等差数列的通项公式.
【分析】由已知结合等差数列的性质求得a5,再由等差数列的前n项和求得答案.
【解答】解:在等差数列{an}中,由a3+a5+a7=15,得3a5=15,∴a5=5.
则.
故答案为:45.
14.已知抛物线y2=4x,P是抛物线上一点,F为焦点,若|PF|=5,则点P的坐标是 (4,4)或(4,﹣4) .
【考点】抛物线的简单性质.
【分析】先设出该点的坐标,根据抛物
( http: / / www.21cnjy.com )线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得x的值,代入抛物线方程求得y.
【解答】解:设该点坐标为(x,y)
根据抛物线定义可知x+1=5,解得x=4,代入抛物线方程求得y=±4
故这点点坐标为:(4,4)或(4,﹣4)
故答案为:(4,4)或(4,﹣4).
15.焦点在x轴上,焦距等于4,且经过点的椭圆标准方程是 .
【考点】椭圆的标准方程.
【分析】设椭圆的方程为(a>b>0),根据题意建立关于a、b的方程组,解出a2、b2的值,即可得到所求椭圆标准方程.
【解答】解:由椭圆的焦点在x轴上,设椭圆的方程为(a>b>0)
∵焦距等于4,且椭圆经过点.
∴,解之得a2=36,b2=32(舍负)
因此,椭圆的标准方程为.
故答案为:
16.数列{an}满足,且a1=1,则通项公式an= 2n﹣1 .
【考点】数列递推式.
【分析】数列{an}满足,化为=2,且a1=1,利用等比数列的通项公式即可得出.
【解答】解:数列{an}满足,
∴=2,且a1=1,
则数列{an}是等比数列,公比为2,首项为1.
则通项公式an=2n﹣1.
故答案为:2n﹣1.
三、解答题(写出必要的文字说明,演算步骤,证明过程)
17.在等比数列{an}中,.
(1)求数列{an}的通项公式;
(2)若分别为等差数列{bn}的第4项和第16项,求数列{bn}的前n项和Sn.
【考点】数列的求和;等比数列的通项公式.
【分析】(1)设等比数列{an}的公比为q,由.可得,解出即可得出.
(2)b4=a3=8,b16=a5=32,可得,解得b1,d.利用求和公式即可得出.
【解答】解:(1)设等比数列{an}的公比为q,∵.∴,解得a1=q=2.∴an=2n.
(2)b4=a3=8,b16=a5=32,∴,解得b1=d=2.
∴Sn=2n+=n2+n.
18.现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
【考点】古典概型及其概率计算公式;列举法计算基本事件数及事件发生的概率.
【分析】(1)根据题意,设事件A为“都是甲类题”,由组合数原理,可得试验结果总数与A包含的基本事件数目,由古典概率公式计算可得答案,
(2)设事件B为“所取的2道题不是
( http: / / www.21cnjy.com )同一类题”,分析可得是组合问题,由组合公式,可得从6件中抽取2道的情况数目与抽出的2道是一个甲类题,一个乙类题的情况数目,由古典概率公式计算可得答案.
【解答】解:(1)从中任取2道题解答,试验结果有=15种;
设事件A为“所取的2道题都是甲类题”,则包含的基本事件共有C=6种,
因此,P(A)=.
(2)设事件B为“所取的2道题不是同一类题”,
从6件中抽取2道,有C62种情况,
而抽出的2道是一个甲类题,一个乙类题的情况数目,有C41 C21=8种情况,
根据古典概型的计算,有P(B)=.
19.在四棱锥P﹣ABCD中,底面是正方形,侧棱PD⊥面ABCD,E是PC中点.
(1)证明PA∥面EDB;
(2)求异面直线PC与AD能成角的大小.
【考点】异面直线及其所成的角;直线与平面平行的判定.
【分析】(1)连接AC交BD于O,连接OE,证明OE∥PA,即可证明PA∥平面EDB;
(2)证明AD⊥平面PCD,即可证明AD⊥PC,可得异面直线PC与AD所成角的大小.
【解答】证明:(1)连接AC交BD于O,连接OE
∵底面ABCD是正方形,∴O为AC中点,
∵在△PAC中,E是PC的中点,
∴OE∥PA,…
∵OE 平面EDB,PA 平面EDB,
∴PA∥平面EDB.…
(2)∵侧棱PD⊥底面ABCD,AD 底面ABCD,
∴PD⊥AD,
∵底面ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,
∴AD⊥平面PCD.…
∴AD⊥PC,
∴异面直线PC与AD所成角为90°.…
20.在△ABC中,角A,B,C的对边分别为.
(Ⅰ)求cosB的值;
(Ⅱ)若,求a和c的值.
【考点】余弦定理;同角三角函数基本关系的运用.
【分析】(1)利用诱导公式求出sin的值,从而利用二倍角的余弦公式求得cosB.
(2)由两个向量的数量积的定义求出ac的值,再利用余弦定理求出a和c的值.
【解答】解:(1)∵cos=,
∴sin=sin(﹣)=,
∴cosB=1﹣2sin2=.
(2)由 =2可得
a c cosB=2,又cosB=,
故ac=6,
由
b2=a2+c2﹣2accosB
可得a2+c2=12,
∴(a﹣c)2=0,
故
a=c,
∴a=c=.
21.某工厂生产某种零件,每个零件成本为40
( http: / / www.21cnjy.com )元,出厂单价为70元.该厂为了鼓励销售商订购,决定当一次订购量超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不能低于61元.
(1)设订购量为x个时,零件的实际出厂单价为y元,写出函数y=f(x)的函数解析式;
(2)当销售商一次订购500个时,该厂获得的利润是多少元?
【考点】分段函数的应用.
【分析】(1)由题意设每个
( http: / / www.21cnjy.com )零件的实际出厂价恰好降为61元时,一次订购量为x0个,则x0=100+,因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为61元;前100件单价为y,当进货件数大于等于550件时,y=61,则当100<x<550时,y=70﹣0.02(x﹣100),得到y为分段函数,写出解析式即可;
(2)设销售商的一次订购量为x个时,工厂获得的利润为L元,表示出L与x的函数关系式,然后令x=500,即可得到对应的利润.
【解答】解:(1)设每个零件的实际出厂价恰好降为61元时,一次订购量为x0个,则x0=100+=550,
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为61元.
当0<x≤100时,y=70;
当100<x<550时,y=70﹣0.02(x﹣100)=72﹣0.02x;
当x≥550时,y=61.
所以y=f(x)=;
(2)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(y﹣40)x=,
当x=500时,L=32×500﹣0.02×5002=11000,
因此,当销售商一次订购500个零件时,该厂获得的利润是11000元.
22.抛物线y2=4x的焦点为F,斜率为1的直线l过点F,且与抛物线相交于A,B两点,M是AB中点.
(1)求弦AB的长;
(2)若MH垂直于准线,垂足为H.求∠AHB的度数.
【考点】抛物线的简单性质.
【分析】(1)根据抛物线
( http: / / www.21cnjy.com )方程求得抛物线的焦点坐标,进而根据点斜式求得直线的方程与抛物线方程联立,消去y,根据韦达定理求得x1+x2=的值,进而根据抛物线的定义可知|AB|=x1++x2+=x1+x2+p,求得答案.
(2)过A,B做准线的垂线,垂足分别为
( http: / / www.21cnjy.com )P,Q,则|AP|=|AF|,|BQ|=|BF|,得出以AB为直径的圆M与准线相切于H,即可得出结论.
【解答】解:(1)抛物线焦点为(1,0),且斜率为1,
则直线方程为y=x﹣1,代入抛物线方程y2=4x得
x2﹣6x+1=0,设A(x1,y1),B(x2,y2)
∴x1+x2=6
根据抛物线的定义可知|AB|=x1++x2+=x1+x2+p=6+2=8;
(2)过A,B做准线的垂线,垂足分别为P,Q,则|AP|=|AF|,|BQ|=|BF|,
∴|AB|=|AF|+|BF|=|AP|+|BQ|,
∵M是AB的中点,
∴|MH|==4,
∴以AB为直径的圆M与准线相切于H,
∴∠AHB=90°.
2017年3月8日
