吉林省延边州汪清六中2016-2017学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 吉林省延边州汪清六中2016-2017学年高二(上)期末数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 15:46:22 | ||
图片预览




文档简介
2016-2017学年吉林省延边州汪清六中高二(上)期末数学试卷(文科)
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.)
1.△ABC的内角A,B,C的对边分别为a,b,c,若c=,b=,B=120°,则c等于( )
A.
B.2
C.
D.
2.在△ABC中,已知a2=b2+c2+bc,则角A为( )
A.
B.
C.
D.或
3.在等比数列{an}中,a2=8,a5=64,则公比q为( )
A.2
B.3
C.4
D.8
4.设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )
A.13
B.49
C.35
D.63
5.某学校组织学生参加英语测试,成绩的频
( http: / / www.21cnjy.com )率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( )
A.45
B.50
C.55
D.60
6.在一个袋子中装有分别标注数字1,2,3
( http: / / www.21cnjy.com ),4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.
B.
C.
D.
7.如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14
B.21
C.28
D.35
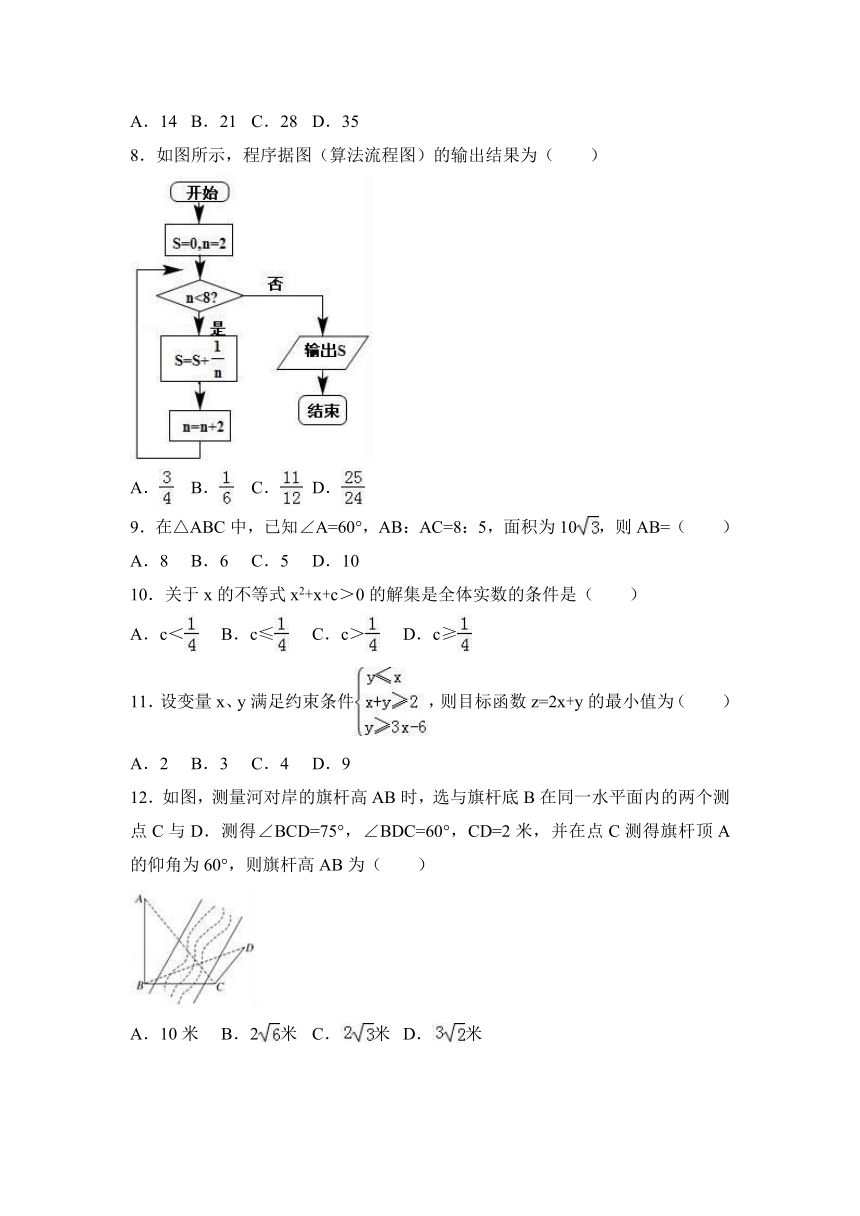
8.如图所示,程序据图(算法流程图)的输出结果为( )
A.
B.
C.
D.
9.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10,则AB=( )
A.8
B.6
C.5
D.10
10.关于x的不等式x2+x+c>0的解集是全体实数的条件是( )
A.c<
B.c≤
C.c>
D.c≥
11.设变量x、y满足约束条件,则目标函数z=2x+y的最小值为( )
A.2
B.3
C.4
D.9
12.如图,测量河对岸的旗杆高AB时,选与
( http: / / www.21cnjy.com )旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
A.10米
B.2米
C.米
D.米
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
13.设集合,则A∩B= .
14.在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,则这三个数为 .
15.在单调递增的等比数列{an}中,a1 a9=64,a3+a7=20,求a11= .
16.当x>﹣1时,函数y=x+的最小值是 .
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅰ)求B的大小;
(Ⅱ)若,c=5,求b.
18.已知不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2}.
(1)计算a、b的值;
(2)求解不等式x2﹣ax+b>0的解集.
19.等比数列{an}中,已知a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
20.为了比较两种治疗失眠
( http: / / www.21cnjy.com )症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6
1.2
2.7
1.5
2.8
1.8
2.2
2.3
3.2
3.5
2.5
2.6
1.2
2.7
1.5
2.9
3.0
3.1
2.3
2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2
1.7
1.9
0.8
0.9
2.4
1.2
2.6
1.3
1.4
1.6
0.5
1.8
0.6
2.1
1.1
2.5
1.2
2.7
0.5
(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
25.动物园要建造一个长方形虎笼,一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围36m长网的材料,当虎笼的长、宽各设计为多少时,可使虎笼面积最大?最大面积为多少?
(2)若使虎笼的面积为32m2,则虎笼的长、宽各设计为多少时,可使围成虎笼所用的钢筋网总长最小?
26.电视传媒公司为了解某地区观众
( http: / / www.21cnjy.com )对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时的间频率分布表(时间单位为:分):
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
频率
0.1
0.18
0.22
0.25
0.2
0.05
将日将收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷
体育迷
合计
男
女
合计
(Ⅱ)将日均收看该体育节目不低于50分钟的观
( http: / / www.21cnjy.com )众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.附:x2=
P(x2≥k)
0.05
0.01
k
3.841
6.635
2016-2017学年吉林省延边州汪清六中高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.)
1.△ABC的内角A,B,C的对边分别为a,b,c,若c=,b=,B=120°,则c等于( )
A.
B.2
C.
D.
【考点】正弦定理.
【分析】根据题意,由正弦定理可得=,变形可得c= sinC,代入数据计算可得答案.
【解答】解:根据题意,△ABC中,c=,b=,B=120°,
由正弦定理可得:
=,即c= sinC=,
即c=;
故选:D.
2.在△ABC中,已知a2=b2+c2+bc,则角A为( )
A.
B.
C.
D.或
【考点】余弦定理.
【分析】根据余弦定理表示出cosA,然后把已知的等式代入即可求出cosA的值,由A的范围,根据特殊角的三角函数值即可得到A的度数.
【解答】解:由a2=b2+c2+bc,
则根据余弦定理得:
cosA===﹣,
因为A∈(0,π),所以A=.
故选C
3.在等比数列{an}中,a2=8,a5=64,则公比q为( )
A.2
B.3
C.4
D.8
【考点】等比数列的通项公式.
【分析】题目给出了a2=8,a5=64,直接利用等比数列的通项公式求解q.
【解答】解:在等比数列{an}中,由,又a2=8,a5=64,
所以,,所以,q=2.
故选A.
4.设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )
A.13
B.49
C.35
D.63
【考点】等差数列的前n项和.
【分析】首先根据已知条件建立方程组求出首项与公差,进一步利用等差数列前n项和公式求出结果.
【解答】解:等差数列{an}中,设首项为a1,公差为d,
,
解得:d=2,a1=1,
所以:
故选:B
5.某学校组织学生参加英语
( http: / / www.21cnjy.com )测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( )
A.45
B.50
C.55
D.60
【考点】频率分布直方图.
【分析】由已知中的频率分
( http: / / www.21cnjy.com )布直方图,我们可以求出成绩低于60分的频率,结合已知中的低于60分的人数是15人,结合频数=频率×总体容量,即可得到总体容量.
【解答】解:∵成绩低于60分有第一、二组数据,
在频率分布直方图中,对应矩形的高分别为0.005,0.01,
每组数据的组距为20
则成绩低于60分的频率P=(0.005+0.010)×20=0.3,
又∵低于60分的人数是15人,
则该班的学生人数是=50.
故选:B.
6.在一个袋子中装有分别标注数字1,2
( http: / / www.21cnjy.com ),3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】从5个小球中选两个有C52种方
( http: / / www.21cnjy.com )法,列举出取出的小球标注的数字之和为3或6的有{1,2},{1,5},{2,4}共3种,根据古典概型公式,代入数据,求出结果.本题也可以不用组合数而只通过列举得到事件总数和满足条件的事件数.
【解答】解:随机取出2个小球得到的结果数有C52=种
取出的小球标注的数字之和为3或6的结果为{1,2},{1,5},{2,4}共3种,
∴P=,
故选A
7.如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14
B.21
C.28
D.35
【考点】等差数列的性质;等差数列的前n项和.
【分析】由等差数列的性质求解.
【解答】解:a3+a4+a5=3a4=12,a4=4,
∴a1+a2+…+a7==7a4=28
故选C
8.如图所示,程序据图(算法流程图)的输出结果为( )
A.
B.
C.
D.
【考点】程序框图.
【分析】根据所给数值执行循环语句,然后判定是否满足判断框中的条件,一旦不满足条件就退出循环,从而到结论.
【解答】解:由程序框图知,循环体被执行后S的值依次为:
第1次S=0+,
第2次S=+,
第3次S=++,此时n=8
不满足选择条件n<8,退出循环,故输出的结果是S=++=.
故选C.
9.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10,则AB=( )
A.8
B.6
C.5
D.10
【考点】余弦定理;正弦定理.
【分析】由已知可得:AC=AB,进而利用三角形面积公式即可计算得解AB的值.
【解答】解:∵AB:AC=8:5,可得:AC=AB,
又∵∠A=60°,面积为10=AB AC sinA=AB×AB×,
∴解得:AB=8.
故选:A.
10.关于x的不等式x2+x+c>0的解集是全体实数的条件是( )
A.c<
B.c≤
C.c>
D.c≥
【考点】二次函数的性质.
【分析】由判别式小于零,求得c的范围.
【解答】解:关于x的不等式x2+x+c>0的解集是全体实数的条件是判别式△=1﹣4c<0,
解得
c>,
故选:C.
11.设变量x、y满足约束条件,则目标函数z=2x+y的最小值为( )
A.2
B.3
C.4
D.9
【考点】简单线性规划的应用.
【分析】本题主要考查线性规划的基本
( http: / / www.21cnjy.com )知识,先画出约束条件的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数Z=2x+y的最小值.
【解答】解:设变量x、y满足约束条件,
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),
则目标函数z=2x+y的最小值为3,
故选B
12.如图,测量河对岸的旗杆高AB时,选
( http: / / www.21cnjy.com )与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
A.10米
B.2米
C.米
D.米
【考点】解三角形的实际应用.
【分析】在△CBD中根据三角形的内角
( http: / / www.21cnjy.com )和定理,求出∠CBD=180°﹣∠BCD﹣∠BDC=45°,从而利用正弦定理求出BC.然后在Rt△ABC中,根据三角函数的定义加以计算,可得旗杆AB的高度.
【解答】解:∵△BCD中,∠BCD=75°,∠BDC=60°,
∴∠CBD=180°﹣∠BCD﹣∠BDC=45°,
在△CBD中,CD=2米,根据正弦定理可得BC==米,
∵Rt△ABC中,∠ACB=60°,
∴AB=BC tan∠ACB= tan60°=3,即旗杆高,3米.
故选:D.
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
13.设集合,则A∩B= (3,4) .
【考点】交集及其运算.
【分析】先利用解分式不等式化简集合B,再根据两个集合的交集的意义求解A∩B.
【解答】解:A={x|x>3},
B={x|<0}={x|1<x<4},
∴A∩B=(3,4),
故答案为:(3,4).
14.在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,则这三个数为 1,3,5 .
【考点】等差数列的通项公式.
【分析】设插入的三个数为a,b,c,则﹣1,a,b,c,7五个数成单调递增的等差数列,利用等差数列的性质能求出这三个数.
【解答】解:在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,
设插入的三个数为a,b,c,
则﹣1,a,b,c,7五个数成单调递增的等差数列,
∴a1=﹣1,a5=﹣1+4d=7,
解得d=2,
∴a=﹣1+2=1,b=﹣1+2×2=3,c=﹣1+2×3=5,
∴这三个数为1,3,5.
故答案为:1,3,5.
15.在单调递增的等比数列{an}中,a1 a9=64,a3+a7=20,求a11= 64 .
【考点】等比数列的通项公式.
【分析】由已知得a3,a7是方程x2﹣
( http: / / www.21cnjy.com )20x+64=0的两个根,且a3<a7,从而求出a3=4,a7=16,再由等比数列通项公式列方程组求出首项和公比,由此能求出a11.
【解答】解:∵单调递增的等比数列{an}中,
a1 a9=64,a3+a7=20,
∴a3 a7=a1 a9=64,
∴a3,a7是方程x2﹣20x+64=0的两个根,且a3<a7,
解方程x2﹣20x+64=0,
得a3=4,a7=16,
∴,解得,
∴a11=a1q10=2×()10=64.
故答案为:64.
16.当x>﹣1时,函数y=x+的最小值是 1 .
【考点】基本不等式在最值问题中的应用.
【分析】变形利用基本不等式的性质即可得出.
【解答】解:∵x>﹣1,
∴函数y=x+=(x+1)+﹣1≥﹣1=1,
当且仅当x+1=,且x>﹣1,即x=0时等号成立,
故函数y的最小值为1.
故答案为:1.
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅰ)求B的大小;
(Ⅱ)若,c=5,求b.
【考点】正弦定理的应用;余弦定理的应用.
【分析】(1)根据正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由△ABC为锐角三角形可得答案.
(2)根据(1)中所求角B的值,和余弦定理直接可求b的值.
【解答】解:(Ⅰ)由a=2bsinA,
根据正弦定理得sinA=2sinBsinA,所以,
由△ABC为锐角三角形得.
(Ⅱ)根据余弦定理,得b2=a2+c2﹣2accosB=27+25﹣45=7.
所以,.
18.已知不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2}.
(1)计算a、b的值;
(2)求解不等式x2﹣ax+b>0的解集.
【考点】一元二次不等式的解法.
【分析】(1)根据不等式ax2+bx﹣1<0的解集,不等式与方程的关系求出a、b的值;
(2)由(1)中a、b的值解对应不等式即可.
【解答】解:(1)∵不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2},
∴方程ax2+bx﹣1=0的两个根为﹣1和2,
将两个根代入方程中得,
解得:a=,b=﹣;
(2)由(1)得不等式为x2﹣x﹣>0,
即2x2﹣x﹣1>0,
∵△=(﹣1)2﹣4×2×(﹣1)=9>0,
∴方程2x2﹣x﹣1=0的两个实数根为:x1=﹣,x2=1;
因而不等式x2﹣x﹣>0的解集是{x|x<﹣或x>1}.
19.等比数列{an}中,已知a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
【考点】等差数列与等比数列的综合.
【分析】(I)由a1=2,a4=16直接求出公比q再代入等比数列的通项公式即可.
(Ⅱ)利用题中条件求出b3=8,b5=32,又由数列{bn}是等差数列求出.再代入求出通项公式及前n项和Sn.
【解答】解:(I)设{an}的公比为q
由已知得16=2q3,解得q=2
∴=2n
(Ⅱ)由(I)得a3=8,a5=32,则b3=8,b5=32
设{bn}的公差为d,则有
解得.
从而bn=﹣16+12(n﹣1)=12n﹣28
所以数列{bn}的前n项和.
20.为了比较两种治疗失眠症的
( http: / / www.21cnjy.com )药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6
1.2
2.7
1.5
2.8
1.8
2.2
2.3
3.2
3.5
2.5
2.6
1.2
2.7
1.5
2.9
3.0
3.1
2.3
2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2
1.7
1.9
0.8
0.9
2.4
1.2
2.6
1.3
1.4
1.6
0.5
1.8
0.6
2.1
1.1
2.5
1.2
2.7
0.5
(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
【考点】众数、中位数、平均数;茎叶图.
【分析】(Ⅰ)利用平均数的计算公式即可得出,据此即可判断出结论;
(Ⅱ)利用已知数据和茎叶图的结构即可完成.
【解答】解:(Ⅰ)设A药观测数据的平均数据的平均数为,设B药观测数据的平均数据的平均数为,
则=×(0.6+1.2+
( http: / / www.21cnjy.com )2.7+1.5+2.8+1.8+2.2+2.3+3.2+3.5+2.5+2.6+1.2+2.7+1.5+2.9+3.0+3.1+2.3+2.4)=2.3.
×(3.2+1.7+1.9+0.8+
( http: / / www.21cnjy.com )0.9+2.4+1.2+2.6+1.3+1.4+1.6+0.5+1.8+0.6+2.1+1.1+2.5+1.2+2.7+0.5)=1.6.
由以上计算结果可知:.由此可看出A药的效果更好.
(Ⅱ)根据两组数据得到下面茎叶图:
从以上茎叶图可以看出,A药疗效的试验结果有的叶集中在2,3上.而B药疗效的试验结果由的叶集中在0,1上.由此可看出A药的疗效更好.
25.动物园要建造一个长方形虎笼,一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围36m长网的材料,当虎笼的长、宽各设计为多少时,可使虎笼面积最大?最大面积为多少?
(2)若使虎笼的面积为32m2,则虎笼的长、宽各设计为多少时,可使围成虎笼所用的钢筋网总长最小?
【考点】基本不等式在最值问题中的应用.
【分析】(1)设每间虎笼的长、宽,利用周长为36m,根据基本不等式,即可求得面积最大值时的长、宽;
(2)设每间虎笼的长、宽,利用面积为32m2,根据周长的表达式,利用基本不等式,即可求得周长最小值时的长、宽.
【解答】解:(1)设虎笼长为x
m,宽为y
m,则由条件,知x+2y=36.
设每间虎笼的面积为S,则S=xy.
由于x+2y≥2=2,
∴2≤36,得xy≤162,即S≤162.
当且仅当x=2y时等号成立.
由解得
故每间虎笼长为18
m,宽为9
m时,可使面积最大,面积最大为162m2.
(2)由条件知S=xy=32.
设钢筋网总长为l,则l=x+2y.
∵x+2y≥2=2=16,
∴l=x+2y≥48,当且仅当x=2y时,等号成立.
由解得
故每间虎笼长8m,宽4m时,可使钢筋网总长最小.
26.电视传媒公司为了解某地区观众对某
( http: / / www.21cnjy.com )类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时的间频率分布表(时间单位为:分):
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
频率
0.1
0.18
0.22
0.25
0.2
0.05
将日将收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷
体育迷
合计
男
女
合计
(Ⅱ)将日均收看该体育节目不低于50分钟
( http: / / www.21cnjy.com )的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.附:x2=
P(x2≥k)
0.05
0.01
k
3.841
6.635
【考点】独立性检验.
【分析】(I)根据所给的频率分布直方图得出数据列出列联表,再代入公式计算得出X方,与3.841比较即可得出结论;
(II)由题意,列出所有的基本事件,计算出事件“任选3人,至少有1人是女性”包含的基本事件数,即可计算出概率.
【解答】解:(I)由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷
体育迷
合计
男
30
15
45
女
45
10
55
合计
75
25
100
…3分
将2×2列联表中的数据代入公式计算,得
X2===≈3.03
因为3.03<3.841,所以没有理由认为“体育迷”与性别有关…6分
(II)由频率分布直方图知,“超级体育迷”为5人,从而一切可能结果所的基本事件空间为
Ω={(a1,a2),(a1,a3),(a2
( http: / / www.21cnjy.com ),a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
其中ai表示男性,i=1,2,3,bi表示女性,i=1,2…9分
Ω由10个基本事件组成,而且这些基本事件的出现是等可能的.用A表示事件“任选3人,至少有1人是女性”.则
A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
事件A有7个基本事件组成,因而P(A)=…12分
2017年3月8日
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.)
1.△ABC的内角A,B,C的对边分别为a,b,c,若c=,b=,B=120°,则c等于( )
A.
B.2
C.
D.
2.在△ABC中,已知a2=b2+c2+bc,则角A为( )
A.
B.
C.
D.或
3.在等比数列{an}中,a2=8,a5=64,则公比q为( )
A.2
B.3
C.4
D.8
4.设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )
A.13
B.49
C.35
D.63
5.某学校组织学生参加英语测试,成绩的频
( http: / / www.21cnjy.com )率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( )
A.45
B.50
C.55
D.60
6.在一个袋子中装有分别标注数字1,2,3
( http: / / www.21cnjy.com ),4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.
B.
C.
D.
7.如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14
B.21
C.28
D.35
8.如图所示,程序据图(算法流程图)的输出结果为( )
A.
B.
C.
D.
9.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10,则AB=( )
A.8
B.6
C.5
D.10
10.关于x的不等式x2+x+c>0的解集是全体实数的条件是( )
A.c<
B.c≤
C.c>
D.c≥
11.设变量x、y满足约束条件,则目标函数z=2x+y的最小值为( )
A.2
B.3
C.4
D.9
12.如图,测量河对岸的旗杆高AB时,选与
( http: / / www.21cnjy.com )旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
A.10米
B.2米
C.米
D.米
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
13.设集合,则A∩B= .
14.在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,则这三个数为 .
15.在单调递增的等比数列{an}中,a1 a9=64,a3+a7=20,求a11= .
16.当x>﹣1时,函数y=x+的最小值是 .
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅰ)求B的大小;
(Ⅱ)若,c=5,求b.
18.已知不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2}.
(1)计算a、b的值;
(2)求解不等式x2﹣ax+b>0的解集.
19.等比数列{an}中,已知a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
20.为了比较两种治疗失眠
( http: / / www.21cnjy.com )症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6
1.2
2.7
1.5
2.8
1.8
2.2
2.3
3.2
3.5
2.5
2.6
1.2
2.7
1.5
2.9
3.0
3.1
2.3
2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2
1.7
1.9
0.8
0.9
2.4
1.2
2.6
1.3
1.4
1.6
0.5
1.8
0.6
2.1
1.1
2.5
1.2
2.7
0.5
(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
25.动物园要建造一个长方形虎笼,一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围36m长网的材料,当虎笼的长、宽各设计为多少时,可使虎笼面积最大?最大面积为多少?
(2)若使虎笼的面积为32m2,则虎笼的长、宽各设计为多少时,可使围成虎笼所用的钢筋网总长最小?
26.电视传媒公司为了解某地区观众
( http: / / www.21cnjy.com )对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时的间频率分布表(时间单位为:分):
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
频率
0.1
0.18
0.22
0.25
0.2
0.05
将日将收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷
体育迷
合计
男
女
合计
(Ⅱ)将日均收看该体育节目不低于50分钟的观
( http: / / www.21cnjy.com )众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.附:x2=
P(x2≥k)
0.05
0.01
k
3.841
6.635
2016-2017学年吉林省延边州汪清六中高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.)
1.△ABC的内角A,B,C的对边分别为a,b,c,若c=,b=,B=120°,则c等于( )
A.
B.2
C.
D.
【考点】正弦定理.
【分析】根据题意,由正弦定理可得=,变形可得c= sinC,代入数据计算可得答案.
【解答】解:根据题意,△ABC中,c=,b=,B=120°,
由正弦定理可得:
=,即c= sinC=,
即c=;
故选:D.
2.在△ABC中,已知a2=b2+c2+bc,则角A为( )
A.
B.
C.
D.或
【考点】余弦定理.
【分析】根据余弦定理表示出cosA,然后把已知的等式代入即可求出cosA的值,由A的范围,根据特殊角的三角函数值即可得到A的度数.
【解答】解:由a2=b2+c2+bc,
则根据余弦定理得:
cosA===﹣,
因为A∈(0,π),所以A=.
故选C
3.在等比数列{an}中,a2=8,a5=64,则公比q为( )
A.2
B.3
C.4
D.8
【考点】等比数列的通项公式.
【分析】题目给出了a2=8,a5=64,直接利用等比数列的通项公式求解q.
【解答】解:在等比数列{an}中,由,又a2=8,a5=64,
所以,,所以,q=2.
故选A.
4.设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则S7等于( )
A.13
B.49
C.35
D.63
【考点】等差数列的前n项和.
【分析】首先根据已知条件建立方程组求出首项与公差,进一步利用等差数列前n项和公式求出结果.
【解答】解:等差数列{an}中,设首项为a1,公差为d,
,
解得:d=2,a1=1,
所以:
故选:B
5.某学校组织学生参加英语
( http: / / www.21cnjy.com )测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( )
A.45
B.50
C.55
D.60
【考点】频率分布直方图.
【分析】由已知中的频率分
( http: / / www.21cnjy.com )布直方图,我们可以求出成绩低于60分的频率,结合已知中的低于60分的人数是15人,结合频数=频率×总体容量,即可得到总体容量.
【解答】解:∵成绩低于60分有第一、二组数据,
在频率分布直方图中,对应矩形的高分别为0.005,0.01,
每组数据的组距为20
则成绩低于60分的频率P=(0.005+0.010)×20=0.3,
又∵低于60分的人数是15人,
则该班的学生人数是=50.
故选:B.
6.在一个袋子中装有分别标注数字1,2
( http: / / www.21cnjy.com ),3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】从5个小球中选两个有C52种方
( http: / / www.21cnjy.com )法,列举出取出的小球标注的数字之和为3或6的有{1,2},{1,5},{2,4}共3种,根据古典概型公式,代入数据,求出结果.本题也可以不用组合数而只通过列举得到事件总数和满足条件的事件数.
【解答】解:随机取出2个小球得到的结果数有C52=种
取出的小球标注的数字之和为3或6的结果为{1,2},{1,5},{2,4}共3种,
∴P=,
故选A
7.如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
A.14
B.21
C.28
D.35
【考点】等差数列的性质;等差数列的前n项和.
【分析】由等差数列的性质求解.
【解答】解:a3+a4+a5=3a4=12,a4=4,
∴a1+a2+…+a7==7a4=28
故选C
8.如图所示,程序据图(算法流程图)的输出结果为( )
A.
B.
C.
D.
【考点】程序框图.
【分析】根据所给数值执行循环语句,然后判定是否满足判断框中的条件,一旦不满足条件就退出循环,从而到结论.
【解答】解:由程序框图知,循环体被执行后S的值依次为:
第1次S=0+,
第2次S=+,
第3次S=++,此时n=8
不满足选择条件n<8,退出循环,故输出的结果是S=++=.
故选C.
9.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10,则AB=( )
A.8
B.6
C.5
D.10
【考点】余弦定理;正弦定理.
【分析】由已知可得:AC=AB,进而利用三角形面积公式即可计算得解AB的值.
【解答】解:∵AB:AC=8:5,可得:AC=AB,
又∵∠A=60°,面积为10=AB AC sinA=AB×AB×,
∴解得:AB=8.
故选:A.
10.关于x的不等式x2+x+c>0的解集是全体实数的条件是( )
A.c<
B.c≤
C.c>
D.c≥
【考点】二次函数的性质.
【分析】由判别式小于零,求得c的范围.
【解答】解:关于x的不等式x2+x+c>0的解集是全体实数的条件是判别式△=1﹣4c<0,
解得
c>,
故选:C.
11.设变量x、y满足约束条件,则目标函数z=2x+y的最小值为( )
A.2
B.3
C.4
D.9
【考点】简单线性规划的应用.
【分析】本题主要考查线性规划的基本
( http: / / www.21cnjy.com )知识,先画出约束条件的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数Z=2x+y的最小值.
【解答】解:设变量x、y满足约束条件,
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),
则目标函数z=2x+y的最小值为3,
故选B
12.如图,测量河对岸的旗杆高AB时,选
( http: / / www.21cnjy.com )与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
A.10米
B.2米
C.米
D.米
【考点】解三角形的实际应用.
【分析】在△CBD中根据三角形的内角
( http: / / www.21cnjy.com )和定理,求出∠CBD=180°﹣∠BCD﹣∠BDC=45°,从而利用正弦定理求出BC.然后在Rt△ABC中,根据三角函数的定义加以计算,可得旗杆AB的高度.
【解答】解:∵△BCD中,∠BCD=75°,∠BDC=60°,
∴∠CBD=180°﹣∠BCD﹣∠BDC=45°,
在△CBD中,CD=2米,根据正弦定理可得BC==米,
∵Rt△ABC中,∠ACB=60°,
∴AB=BC tan∠ACB= tan60°=3,即旗杆高,3米.
故选:D.
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
13.设集合,则A∩B= (3,4) .
【考点】交集及其运算.
【分析】先利用解分式不等式化简集合B,再根据两个集合的交集的意义求解A∩B.
【解答】解:A={x|x>3},
B={x|<0}={x|1<x<4},
∴A∩B=(3,4),
故答案为:(3,4).
14.在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,则这三个数为 1,3,5 .
【考点】等差数列的通项公式.
【分析】设插入的三个数为a,b,c,则﹣1,a,b,c,7五个数成单调递增的等差数列,利用等差数列的性质能求出这三个数.
【解答】解:在﹣1和7中间插入三个数,使得这五个数成单调递增的等差数列,
设插入的三个数为a,b,c,
则﹣1,a,b,c,7五个数成单调递增的等差数列,
∴a1=﹣1,a5=﹣1+4d=7,
解得d=2,
∴a=﹣1+2=1,b=﹣1+2×2=3,c=﹣1+2×3=5,
∴这三个数为1,3,5.
故答案为:1,3,5.
15.在单调递增的等比数列{an}中,a1 a9=64,a3+a7=20,求a11= 64 .
【考点】等比数列的通项公式.
【分析】由已知得a3,a7是方程x2﹣
( http: / / www.21cnjy.com )20x+64=0的两个根,且a3<a7,从而求出a3=4,a7=16,再由等比数列通项公式列方程组求出首项和公比,由此能求出a11.
【解答】解:∵单调递增的等比数列{an}中,
a1 a9=64,a3+a7=20,
∴a3 a7=a1 a9=64,
∴a3,a7是方程x2﹣20x+64=0的两个根,且a3<a7,
解方程x2﹣20x+64=0,
得a3=4,a7=16,
∴,解得,
∴a11=a1q10=2×()10=64.
故答案为:64.
16.当x>﹣1时,函数y=x+的最小值是 1 .
【考点】基本不等式在最值问题中的应用.
【分析】变形利用基本不等式的性质即可得出.
【解答】解:∵x>﹣1,
∴函数y=x+=(x+1)+﹣1≥﹣1=1,
当且仅当x+1=,且x>﹣1,即x=0时等号成立,
故函数y的最小值为1.
故答案为:1.
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅰ)求B的大小;
(Ⅱ)若,c=5,求b.
【考点】正弦定理的应用;余弦定理的应用.
【分析】(1)根据正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由△ABC为锐角三角形可得答案.
(2)根据(1)中所求角B的值,和余弦定理直接可求b的值.
【解答】解:(Ⅰ)由a=2bsinA,
根据正弦定理得sinA=2sinBsinA,所以,
由△ABC为锐角三角形得.
(Ⅱ)根据余弦定理,得b2=a2+c2﹣2accosB=27+25﹣45=7.
所以,.
18.已知不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2}.
(1)计算a、b的值;
(2)求解不等式x2﹣ax+b>0的解集.
【考点】一元二次不等式的解法.
【分析】(1)根据不等式ax2+bx﹣1<0的解集,不等式与方程的关系求出a、b的值;
(2)由(1)中a、b的值解对应不等式即可.
【解答】解:(1)∵不等式ax2+bx﹣1<0的解集为{x|﹣1<x<2},
∴方程ax2+bx﹣1=0的两个根为﹣1和2,
将两个根代入方程中得,
解得:a=,b=﹣;
(2)由(1)得不等式为x2﹣x﹣>0,
即2x2﹣x﹣1>0,
∵△=(﹣1)2﹣4×2×(﹣1)=9>0,
∴方程2x2﹣x﹣1=0的两个实数根为:x1=﹣,x2=1;
因而不等式x2﹣x﹣>0的解集是{x|x<﹣或x>1}.
19.等比数列{an}中,已知a1=2,a4=16
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
【考点】等差数列与等比数列的综合.
【分析】(I)由a1=2,a4=16直接求出公比q再代入等比数列的通项公式即可.
(Ⅱ)利用题中条件求出b3=8,b5=32,又由数列{bn}是等差数列求出.再代入求出通项公式及前n项和Sn.
【解答】解:(I)设{an}的公比为q
由已知得16=2q3,解得q=2
∴=2n
(Ⅱ)由(I)得a3=8,a5=32,则b3=8,b5=32
设{bn}的公差为d,则有
解得.
从而bn=﹣16+12(n﹣1)=12n﹣28
所以数列{bn}的前n项和.
20.为了比较两种治疗失眠症的
( http: / / www.21cnjy.com )药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6
1.2
2.7
1.5
2.8
1.8
2.2
2.3
3.2
3.5
2.5
2.6
1.2
2.7
1.5
2.9
3.0
3.1
2.3
2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2
1.7
1.9
0.8
0.9
2.4
1.2
2.6
1.3
1.4
1.6
0.5
1.8
0.6
2.1
1.1
2.5
1.2
2.7
0.5
(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
【考点】众数、中位数、平均数;茎叶图.
【分析】(Ⅰ)利用平均数的计算公式即可得出,据此即可判断出结论;
(Ⅱ)利用已知数据和茎叶图的结构即可完成.
【解答】解:(Ⅰ)设A药观测数据的平均数据的平均数为,设B药观测数据的平均数据的平均数为,
则=×(0.6+1.2+
( http: / / www.21cnjy.com )2.7+1.5+2.8+1.8+2.2+2.3+3.2+3.5+2.5+2.6+1.2+2.7+1.5+2.9+3.0+3.1+2.3+2.4)=2.3.
×(3.2+1.7+1.9+0.8+
( http: / / www.21cnjy.com )0.9+2.4+1.2+2.6+1.3+1.4+1.6+0.5+1.8+0.6+2.1+1.1+2.5+1.2+2.7+0.5)=1.6.
由以上计算结果可知:.由此可看出A药的效果更好.
(Ⅱ)根据两组数据得到下面茎叶图:
从以上茎叶图可以看出,A药疗效的试验结果有的叶集中在2,3上.而B药疗效的试验结果由的叶集中在0,1上.由此可看出A药的疗效更好.
25.动物园要建造一个长方形虎笼,一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围36m长网的材料,当虎笼的长、宽各设计为多少时,可使虎笼面积最大?最大面积为多少?
(2)若使虎笼的面积为32m2,则虎笼的长、宽各设计为多少时,可使围成虎笼所用的钢筋网总长最小?
【考点】基本不等式在最值问题中的应用.
【分析】(1)设每间虎笼的长、宽,利用周长为36m,根据基本不等式,即可求得面积最大值时的长、宽;
(2)设每间虎笼的长、宽,利用面积为32m2,根据周长的表达式,利用基本不等式,即可求得周长最小值时的长、宽.
【解答】解:(1)设虎笼长为x
m,宽为y
m,则由条件,知x+2y=36.
设每间虎笼的面积为S,则S=xy.
由于x+2y≥2=2,
∴2≤36,得xy≤162,即S≤162.
当且仅当x=2y时等号成立.
由解得
故每间虎笼长为18
m,宽为9
m时,可使面积最大,面积最大为162m2.
(2)由条件知S=xy=32.
设钢筋网总长为l,则l=x+2y.
∵x+2y≥2=2=16,
∴l=x+2y≥48,当且仅当x=2y时,等号成立.
由解得
故每间虎笼长8m,宽4m时,可使钢筋网总长最小.
26.电视传媒公司为了解某地区观众对某
( http: / / www.21cnjy.com )类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时的间频率分布表(时间单位为:分):
分组
[0,10)
[10,20)
[20,30)
[30,40)
[40,50)
[50,60)
频率
0.1
0.18
0.22
0.25
0.2
0.05
将日将收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷
体育迷
合计
男
女
合计
(Ⅱ)将日均收看该体育节目不低于50分钟
( http: / / www.21cnjy.com )的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.附:x2=
P(x2≥k)
0.05
0.01
k
3.841
6.635
【考点】独立性检验.
【分析】(I)根据所给的频率分布直方图得出数据列出列联表,再代入公式计算得出X方,与3.841比较即可得出结论;
(II)由题意,列出所有的基本事件,计算出事件“任选3人,至少有1人是女性”包含的基本事件数,即可计算出概率.
【解答】解:(I)由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷
体育迷
合计
男
30
15
45
女
45
10
55
合计
75
25
100
…3分
将2×2列联表中的数据代入公式计算,得
X2===≈3.03
因为3.03<3.841,所以没有理由认为“体育迷”与性别有关…6分
(II)由频率分布直方图知,“超级体育迷”为5人,从而一切可能结果所的基本事件空间为
Ω={(a1,a2),(a1,a3),(a2
( http: / / www.21cnjy.com ),a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
其中ai表示男性,i=1,2,3,bi表示女性,i=1,2…9分
Ω由10个基本事件组成,而且这些基本事件的出现是等可能的.用A表示事件“任选3人,至少有1人是女性”.则
A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}
事件A有7个基本事件组成,因而P(A)=…12分
2017年3月8日
