黑龙江省友谊县红兴隆管理局第一高级中学2016-2017学年高二下学期开学考试数学(理)试题 Word版含答案
文档属性
| 名称 | 黑龙江省友谊县红兴隆管理局第一高级中学2016-2017学年高二下学期开学考试数学(理)试题 Word版含答案 | 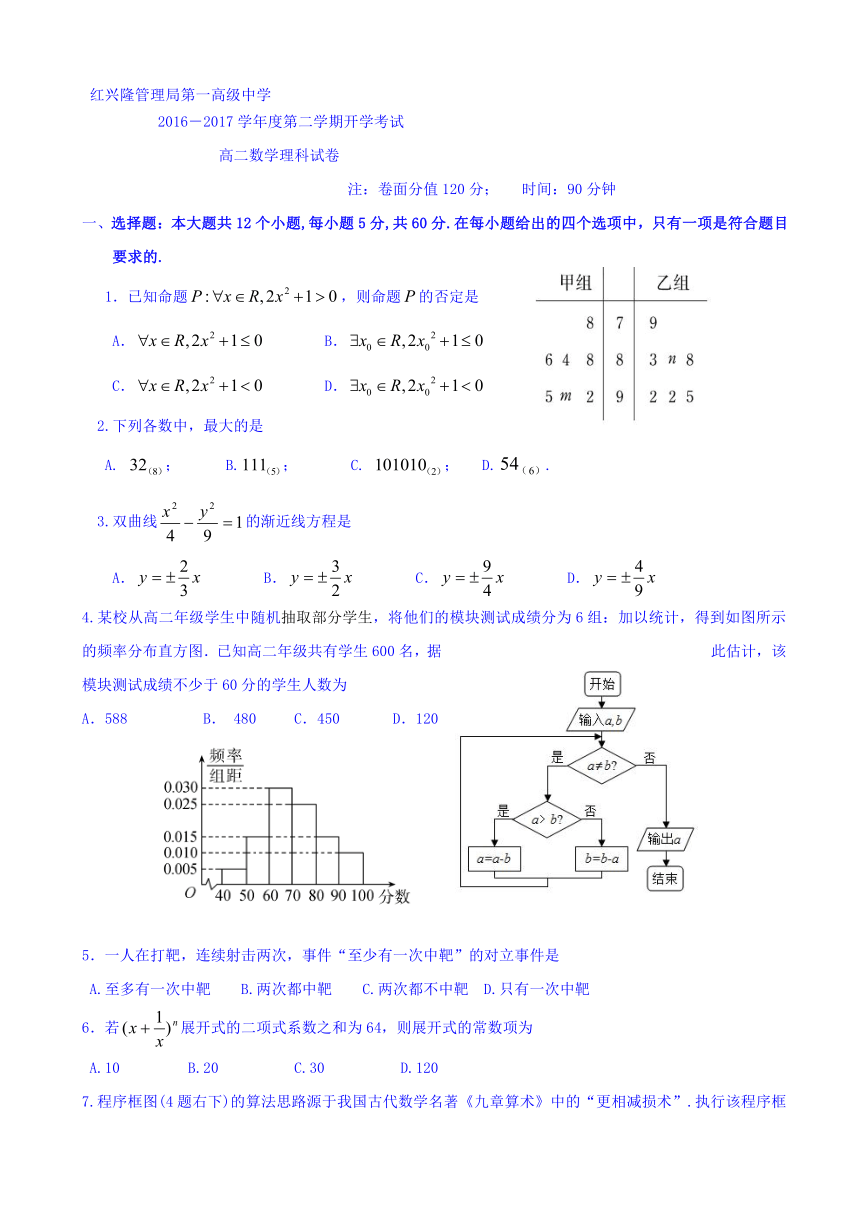 | |
| 格式 | zip | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 07:41:56 | ||
图片预览



文档简介
红兴隆管理局第一高级中学
2016-2017学年度第二学期开学考试
高二数学理科试卷
注:卷面分值120分;
时间:90分钟
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知命题,则命题的否定是
A.
B.
C.
D.
2.下列各数中,最大的是
A.
;
B.;
C.
;
D..
3.双曲线的渐近线方程是
A.
B.
C.
D.
4.某校从高二年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
A.588
B.
480
C.450
D.120
5.一人在打靶,连续射击两次,事件“至少有一次中靶”的对立事件是
A.至多有一次中靶 B.两次都中靶 C.两次都不中靶 D.只有一次中靶
6.若展开式的二项式系数之和为64,则展开式的常数项为
A.10
B.20
C.30
D.120
7.程序框图(4题右下)的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的分别为63,98,则输出的
A.7
B.3
C.9
D.14
8.已知抛物线的准线经过点(-1,1),则该抛物线的焦点坐标为
A.(-1,0)
B.(1,0)
C.(0,-1)
D.(0,1)
9.某学校数学兴趣班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图(1题右侧)所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则的值是
A.10
B.11
C.12
D.13
10.命题“对任意实数,关于的不等式恒成立”为真命题的一个必要不充分条件是
A.
B.
C.
D.
11.在区间上任取一个数,则函数的值不小于0的概率为
A.
B.
C.
D.
12.已知下面四个命题:
(1)从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项
指标检测,这样的抽样是系统抽样;(2)两个随机变量相关性越强,则相关系数的
绝对值越接近于1;(3)对分类变量X和Y的随机变量的观测值来说,越小,
“X与Y有关系”的把握程度越大;(4)在回归直线方程=0.4x+12中,当解释变量
每增加一个单位时,预报变量大约增加0.4个单位.
其中真命题的个数是
A.0
B.1
C.2
D.3
二、填空题(本大题共4个小题,每小题5分,共20分)
13.若向量,且,则等于
.
8
12
13
18
10
8
6
7
4
14.有一组数据:已知对呈线性相关关系为:,则的值为
.
15.从6人中选出4人分别到巴黎,伦敦,悉尼,莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲,乙两人不去巴黎游览,则不同的选择方案共有
.
种.(用数字作答)
16.已知直线与椭圆相交于两点,且线段的
中点在直线上,
此椭圆的离心率为
.
三、解答题(本大题共4小题,共40分,解答应写出必要的文字说明、证明过程或演算步骤)
商店名称
销售额(千万元)
3
5
6
7
9
利润额(千万元)
2
3
3
4
5
17.(本小题满分8分)
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(Ⅰ)用最小二乘法计算利润额对销售额的回归直线方程;
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
(注:==,)
(本小题满分10分)
有2
000名网购者在11月11日当天于某购物网站进行网购消费(消费金额不超过1
000元),其中有女士1
100名,男士900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2
000名网购者中抽取200名进行分析,如下表.(消费金额单位:元)
女士消费情况:
消费金额
(0,200)
[200,400)
[400,600)
[600,800)
人数
10
25
35
30
x
男士消费情况:
消费金额
(0,200)
[200,400)
[400,600)
[600,800)
人数
15
30
25
y
5
(1)计算x,y的值,在抽出的200名且消费金额在(单位:元)的网购者中随机选出2名发放网购红包,求选出的2名网购者都是男士的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写下面2×2列联表(请学生自己用答卷笔画在答题卡上),并回答能否在犯错误的概率不超过0.05的前提下认为“是否为‘网购达人’与性别有关”?
女士
男士
总计
网购达人
非网购达人
总计
附:
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
k0
2.706
3.841
5.024
6.635
7.879
K2=,n=a+b+c+d
19.(本小题满分10分)
如图所示,在长方体ABCD
A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
(1)求异面直线D1E与A1D所成的角;
(2)若二面角D1
EC
D的大小为45°,求点B到平面D1EC的距离.
20.(本小题满分12分)
已知椭圆的左右焦点分别为,
抛物线与椭圆有相同的焦点,且椭圆过点.
(I)求椭圆的标准方程;
(Ⅱ)若椭圆的右顶点为,直线交椭圆于、两点
(、与点不重合),且满足,若点为中点,求直线斜率的最大值.
红兴隆管理局第一高级中学2016—2017学年度第二学期开学考试
高二数学理科答案
一、选择题:本大题共12小题
,
每小题5分,
共60分。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
B
C
B
A
B
C
D
A
D
二、填空题(共4小题,每小题5分,共20分)
13.6
14.14
15.240
16.
三、解答题(本大题共4小题,共40分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分8分)
解
(1)设回归直线的方程是:,,
∴
,
∴对销售额的回归直线方程为:;——————6分
(2)当销售额为4(千万元)时,利润额为:(千万元).
———8分
18.(本小题满分10分)
解:(1)依题意,女士应抽取110名,男士应抽取90名,故x=10,y=15.
消费金额在(单位:元)的网购者共有15名,从中选出2名共有105种选法,若2名网购者都是男士,共有10种选法,所以选出的2名网购者都是男士的概率为=.
——————5分
(2)列联表如下:
女士
男士
总计
网购达人
40
20
60
非网购达人
70
70
140
总计
110
90
200
又因为4.714>3.841,故能在犯错误的概率不超过0.05的前提下认为“是否为‘网购达人’与性别有关”.—————10分
19.(本小题满分10分)
解:以D为坐标原点,分别以,,所在方向为x轴、y轴、z轴的正方向建立空间直角坐标系.
(1)由A1(1,0,1),得=(1,0,1).
设E(1,a,0),由D1(0,0,1),得=(1,a,-1).
又·=1+0-1=0,所以⊥,即D1E与A1D所成的角为90°.—————4分
(2)由题意可知m=(0,0,1)为平面DEC的一个法向量,设n=(x,y,z)为平面CED1的法向量.
由|cos〈m,n〉|==cos
45°=,
得到z2=x2+y2.①
由C(0,2,0),得=(0,2,-1),根据n⊥,即n·=0,
得到2y-z=0.②
联立①②,令y=1,可得n=(,1,2),
故点B(1,2,0)到平面D1EC的距离d===.—————10分
20.(本小题满分12分)
已知椭圆的左右焦点分别为,
抛物线与椭圆有相同的焦点,且椭圆过点.
(I)求椭圆的标准方程;
(Ⅱ)若椭圆的右顶点为,直线交椭圆于、两点
(、与点不重合),且满足,若点为中点,求直线斜率的最大值.
20.
(Ⅰ)由题意可得a=2,2c=2,即c=1,b==,
则椭圆的标准方程为+=1;——————4分
(Ⅱ)设直线AE的方程为y=k(x﹣2),代入椭圆方程,可得(3+4k2)x2﹣16k2x+16k2﹣12=0,
由2+xE=,可得xE=,yE=k(xE﹣2)=,
由于AE⊥AF,只要将上式的k换为﹣,可得xF=,yF=,
由2=+,可得P为EF的中点,
即有P(,),
则直线AP的斜率为t==,
当k=0时,t=0;当k≠0时,t=,
再令s=﹣k,可得t=,当s=0时,t=0;当s>0时,t=≤=,
当且仅当4s=时,取得最大值;
综上可得直线AP的斜率的最大值为.
———12分
2016-2017学年度第二学期开学考试
高二数学理科试卷
注:卷面分值120分;
时间:90分钟
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知命题,则命题的否定是
A.
B.
C.
D.
2.下列各数中,最大的是
A.
;
B.;
C.
;
D..
3.双曲线的渐近线方程是
A.
B.
C.
D.
4.某校从高二年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
A.588
B.
480
C.450
D.120
5.一人在打靶,连续射击两次,事件“至少有一次中靶”的对立事件是
A.至多有一次中靶 B.两次都中靶 C.两次都不中靶 D.只有一次中靶
6.若展开式的二项式系数之和为64,则展开式的常数项为
A.10
B.20
C.30
D.120
7.程序框图(4题右下)的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的分别为63,98,则输出的
A.7
B.3
C.9
D.14
8.已知抛物线的准线经过点(-1,1),则该抛物线的焦点坐标为
A.(-1,0)
B.(1,0)
C.(0,-1)
D.(0,1)
9.某学校数学兴趣班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图(1题右侧)所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则的值是
A.10
B.11
C.12
D.13
10.命题“对任意实数,关于的不等式恒成立”为真命题的一个必要不充分条件是
A.
B.
C.
D.
11.在区间上任取一个数,则函数的值不小于0的概率为
A.
B.
C.
D.
12.已知下面四个命题:
(1)从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项
指标检测,这样的抽样是系统抽样;(2)两个随机变量相关性越强,则相关系数的
绝对值越接近于1;(3)对分类变量X和Y的随机变量的观测值来说,越小,
“X与Y有关系”的把握程度越大;(4)在回归直线方程=0.4x+12中,当解释变量
每增加一个单位时,预报变量大约增加0.4个单位.
其中真命题的个数是
A.0
B.1
C.2
D.3
二、填空题(本大题共4个小题,每小题5分,共20分)
13.若向量,且,则等于
.
8
12
13
18
10
8
6
7
4
14.有一组数据:已知对呈线性相关关系为:,则的值为
.
15.从6人中选出4人分别到巴黎,伦敦,悉尼,莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲,乙两人不去巴黎游览,则不同的选择方案共有
.
种.(用数字作答)
16.已知直线与椭圆相交于两点,且线段的
中点在直线上,
此椭圆的离心率为
.
三、解答题(本大题共4小题,共40分,解答应写出必要的文字说明、证明过程或演算步骤)
商店名称
销售额(千万元)
3
5
6
7
9
利润额(千万元)
2
3
3
4
5
17.(本小题满分8分)
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(Ⅰ)用最小二乘法计算利润额对销售额的回归直线方程;
(Ⅱ)当销售额为4(千万元)时,估计利润额的大小.
(注:==,)
(本小题满分10分)
有2
000名网购者在11月11日当天于某购物网站进行网购消费(消费金额不超过1
000元),其中有女士1
100名,男士900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2
000名网购者中抽取200名进行分析,如下表.(消费金额单位:元)
女士消费情况:
消费金额
(0,200)
[200,400)
[400,600)
[600,800)
人数
10
25
35
30
x
男士消费情况:
消费金额
(0,200)
[200,400)
[400,600)
[600,800)
人数
15
30
25
y
5
(1)计算x,y的值,在抽出的200名且消费金额在(单位:元)的网购者中随机选出2名发放网购红包,求选出的2名网购者都是男士的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写下面2×2列联表(请学生自己用答卷笔画在答题卡上),并回答能否在犯错误的概率不超过0.05的前提下认为“是否为‘网购达人’与性别有关”?
女士
男士
总计
网购达人
非网购达人
总计
附:
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
k0
2.706
3.841
5.024
6.635
7.879
K2=,n=a+b+c+d
19.(本小题满分10分)
如图所示,在长方体ABCD
A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
(1)求异面直线D1E与A1D所成的角;
(2)若二面角D1
EC
D的大小为45°,求点B到平面D1EC的距离.
20.(本小题满分12分)
已知椭圆的左右焦点分别为,
抛物线与椭圆有相同的焦点,且椭圆过点.
(I)求椭圆的标准方程;
(Ⅱ)若椭圆的右顶点为,直线交椭圆于、两点
(、与点不重合),且满足,若点为中点,求直线斜率的最大值.
红兴隆管理局第一高级中学2016—2017学年度第二学期开学考试
高二数学理科答案
一、选择题:本大题共12小题
,
每小题5分,
共60分。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
B
C
B
A
B
C
D
A
D
二、填空题(共4小题,每小题5分,共20分)
13.6
14.14
15.240
16.
三、解答题(本大题共4小题,共40分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分8分)
解
(1)设回归直线的方程是:,,
∴
,
∴对销售额的回归直线方程为:;——————6分
(2)当销售额为4(千万元)时,利润额为:(千万元).
———8分
18.(本小题满分10分)
解:(1)依题意,女士应抽取110名,男士应抽取90名,故x=10,y=15.
消费金额在(单位:元)的网购者共有15名,从中选出2名共有105种选法,若2名网购者都是男士,共有10种选法,所以选出的2名网购者都是男士的概率为=.
——————5分
(2)列联表如下:
女士
男士
总计
网购达人
40
20
60
非网购达人
70
70
140
总计
110
90
200
又因为4.714>3.841,故能在犯错误的概率不超过0.05的前提下认为“是否为‘网购达人’与性别有关”.—————10分
19.(本小题满分10分)
解:以D为坐标原点,分别以,,所在方向为x轴、y轴、z轴的正方向建立空间直角坐标系.
(1)由A1(1,0,1),得=(1,0,1).
设E(1,a,0),由D1(0,0,1),得=(1,a,-1).
又·=1+0-1=0,所以⊥,即D1E与A1D所成的角为90°.—————4分
(2)由题意可知m=(0,0,1)为平面DEC的一个法向量,设n=(x,y,z)为平面CED1的法向量.
由|cos〈m,n〉|==cos
45°=,
得到z2=x2+y2.①
由C(0,2,0),得=(0,2,-1),根据n⊥,即n·=0,
得到2y-z=0.②
联立①②,令y=1,可得n=(,1,2),
故点B(1,2,0)到平面D1EC的距离d===.—————10分
20.(本小题满分12分)
已知椭圆的左右焦点分别为,
抛物线与椭圆有相同的焦点,且椭圆过点.
(I)求椭圆的标准方程;
(Ⅱ)若椭圆的右顶点为,直线交椭圆于、两点
(、与点不重合),且满足,若点为中点,求直线斜率的最大值.
20.
(Ⅰ)由题意可得a=2,2c=2,即c=1,b==,
则椭圆的标准方程为+=1;——————4分
(Ⅱ)设直线AE的方程为y=k(x﹣2),代入椭圆方程,可得(3+4k2)x2﹣16k2x+16k2﹣12=0,
由2+xE=,可得xE=,yE=k(xE﹣2)=,
由于AE⊥AF,只要将上式的k换为﹣,可得xF=,yF=,
由2=+,可得P为EF的中点,
即有P(,),
则直线AP的斜率为t==,
当k=0时,t=0;当k≠0时,t=,
再令s=﹣k,可得t=,当s=0时,t=0;当s>0时,t=≤=,
当且仅当4s=时,取得最大值;
综上可得直线AP的斜率的最大值为.
———12分
同课章节目录
