17.5.1 一次函数、反比例函数的实际应用 同步练习
文档属性
| 名称 | 17.5.1 一次函数、反比例函数的实际应用 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 465.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 21:50:37 | ||
图片预览


文档简介
17.5.1 一次函数、反比例函数的实际应用
核心笔记: 建立函数模型:把待解决的实际问题的数量关系抽象为一次函数或反比例函数,即所谓的建立函数模型.在运用函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数或反比例函数关系.当确定是一次函数或反比例函数关系时,可求出表达式,并运用一次函数或反比例函数的图象和性质进一步求得所需要的结果.
基础训练
1.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数关系式和自变量取值范围分别是( )www.21-cn-jy.com
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
2.小华以每分钟x个字的速度书写,y分钟写了300个字,则y与x的函数关系式为( )
A.y= B.y=300x
C.x+y=300 D.y=
3.在一定范围内,弹簧的长度y(cm)与它所挂的物体的质量x(g)之间满足表达式y=kx+b,已知所挂物体的质量为50 g时,弹簧长12.5 cm,所挂物体的质量为200 g时,弹簧长20 cm,那么当弹簧长15 cm时,所挂物体的质量为( )2·1·c·n·j·y
A.80 g B.100 g
C.120 g D.150 g
4.某单位要建一个200平方米的长方形草坪,已知它的长是y米,宽是x米,则y与x之间的函数关系式为y=,当它的长为25米时,它的宽为________________.2-1-c-n-j-y
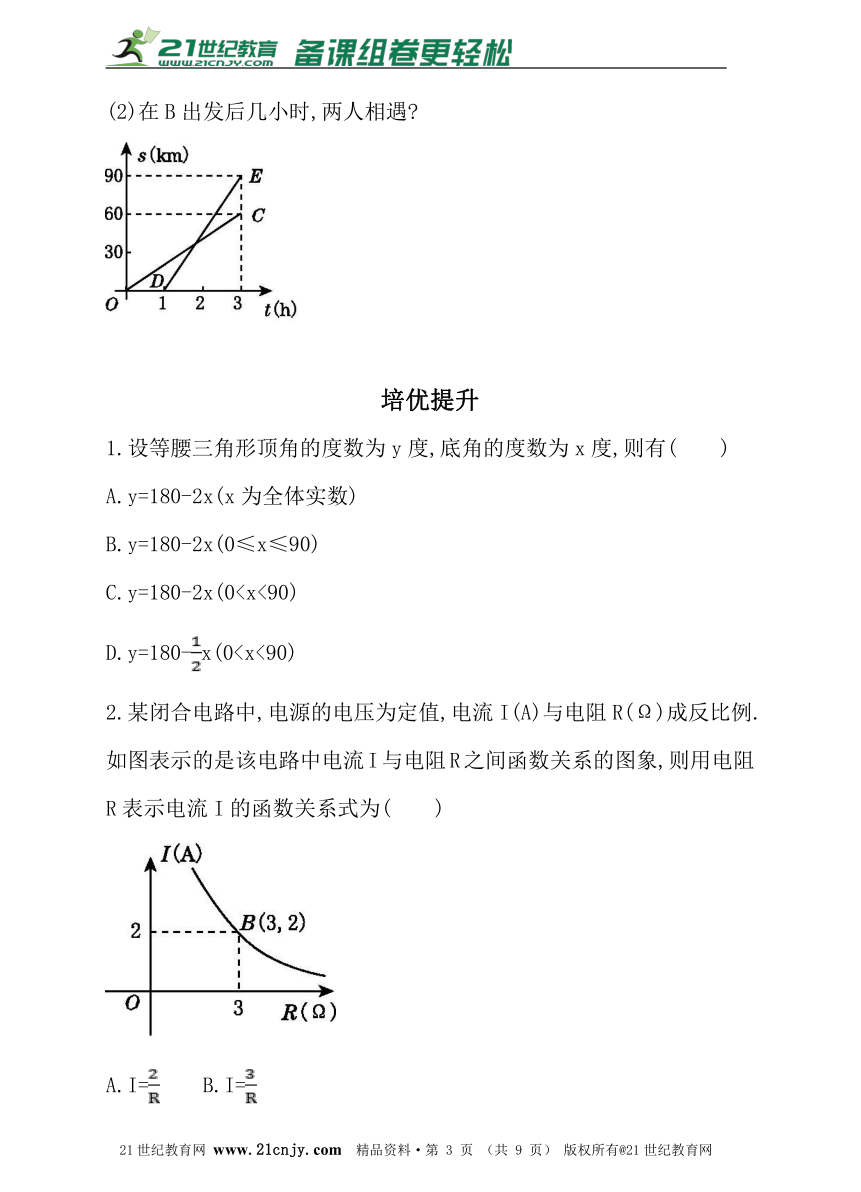
5.一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示.当0≤x≤1时,y关于x的函数表达式为y=60x,那么当16.已知甲、乙两地相距90 km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
培优提升
1.设等腰三角形顶角的度数为y度,底角的度数为x度,则有( )
A.y=180-2x(x为全体实数)
B.y=180-2x(0≤x≤90)
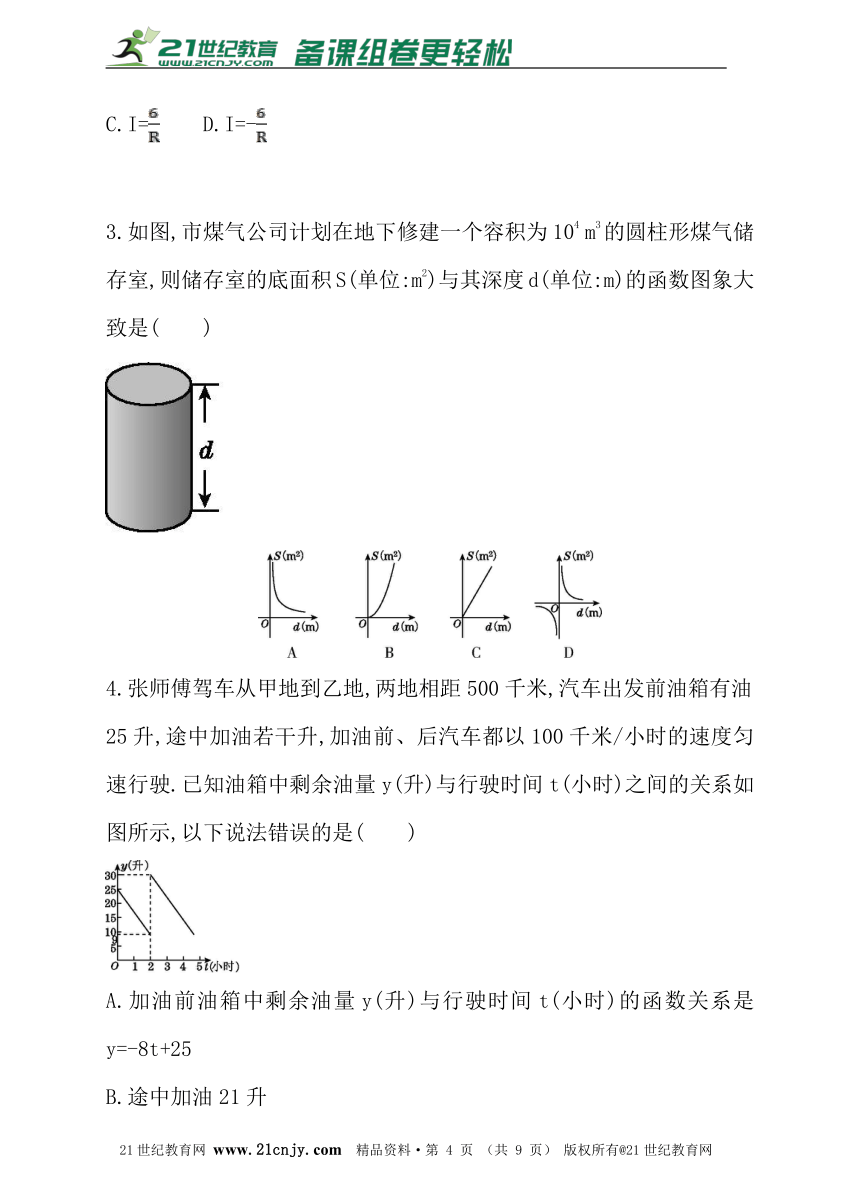
C.y=180-2x(0D.y=180-x(02.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数关系式为( )21cnjy.com
A.I= B.I=
C.I= D.I=-
3.如图,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )21·世纪*教育网
4.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶.已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示,以下说法错误的是( )www-2-1-cnjy-com
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=-8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
5.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人间的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123,其中正确的是( )【来源:21·世纪·教育·网】
A.①②③ B.①② C.①③ D.②③
6.某天,为按计划准点到达某个海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是 .21世纪教育网版权所有
7.新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.21*cnjy*com
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
参考答案
【基础训练】
1.【答案】D 2.【答案】A
3.【答案】B 4.【答案】8米
5.【答案】y=100x-40
解:∵当0≤x≤1时,y关于x的函数表达式为y=60x,∴当x=1时,y=60.又∵当x=2时,y=160,∴当16.解:(1)A比B后出发1 h,B的速度是20 km/h.
(2)设直线DE对应的函数表达式为s=kt+b.
把D(1,0),E(3,90)的坐标分别代入得解得
∴直线DE对应的函数表达式为s=45t-45.
∵直线OC对应的函数表达式为s=20t.
由解得
∴在B出发后1.8 h,两人相遇.
【培优提升】
1.【答案】C
解:根据三角形内角和为180° 得y+2x=180,变形得y=180-2x,自变量x的取值范围为02.【答案】C 3.【答案】A
4.【答案】C
解:A.设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b,
将(0,25),(2,9)代入,得解得
所以y=-8t+25,正确,故本选项不符合题意;B.由函数图象可知,途中加油30-9=21(升),正确,故本选项不符合题意;C.由函数图象可知,汽车每小时用油(25-9)÷2=8(升),所以汽车加油后还可行驶30÷8=3(小时),3<4,错误,故本选项符合题意;D.汽车从甲地到达乙地,所需时间为500÷100=5(小时),5小时耗油量为8×5=40(升),∵汽车出发前油箱有油25升,途中加油21升,∴汽车到达乙地时油箱中还余油25+21-40=6(升),正确,故本选项不符合题意.故选C.
5.【答案】A
解:乙出发时甲跑了2 s,相距8 m,所以甲的速度为4 m/s.100 s后乙开始休息,所以乙的速度是500÷100=5(m/s).a s后甲、乙相遇,所以a==8,故①正确.100 s后乙到达终点,甲跑了4×(100+2)=408(m),所以b=500-408=92,故②正确.甲到达终点一共用时500÷4=125(s),所以c=125-2=123.故③正确.故选A.【出处:21教育名师】
6.【答案】7:00
解:由函数图象及题意,得故障前的速度为80÷1=80(海里/小时),故障后的速度为(180-80)÷1=100(海里/小时).设全程长为a海里,由题意,得=2+,解得a=480,21教育网
则原计划行驶的时间为480÷80=6(小时),
故原计划准点到达的时刻为7:00.
7.解:(1)当1≤x≤8时,y=4000-30(8-x)=4000-240+30x=30x+3760;
当8∴所求函数关系式为
y=
(2)当x=16时,
方案一每套楼房总费用:
w1=120(50×16+3600)×92%-a=485760-a;
方案二每套楼房总费用:
w2=120(50×16+3600)×90%=475200.
∴当w110560;
当w1=w2时,即485760-a=475 200时,a=10560;
当w1>w2时,即485760-a>475 200时,a<10560.
因此,当每套赠送的装修基金多于10560元时,选择方案一合算;
当每套赠送的装修基金等于10560元时,两种方案一样;
当每套赠送的装修基金少于10560元时,选择方案二合算.
核心笔记: 建立函数模型:把待解决的实际问题的数量关系抽象为一次函数或反比例函数,即所谓的建立函数模型.在运用函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数或反比例函数关系.当确定是一次函数或反比例函数关系时,可求出表达式,并运用一次函数或反比例函数的图象和性质进一步求得所需要的结果.
基础训练
1.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数关系式和自变量取值范围分别是( )www.21-cn-jy.com
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
2.小华以每分钟x个字的速度书写,y分钟写了300个字,则y与x的函数关系式为( )
A.y= B.y=300x
C.x+y=300 D.y=
3.在一定范围内,弹簧的长度y(cm)与它所挂的物体的质量x(g)之间满足表达式y=kx+b,已知所挂物体的质量为50 g时,弹簧长12.5 cm,所挂物体的质量为200 g时,弹簧长20 cm,那么当弹簧长15 cm时,所挂物体的质量为( )2·1·c·n·j·y
A.80 g B.100 g
C.120 g D.150 g
4.某单位要建一个200平方米的长方形草坪,已知它的长是y米,宽是x米,则y与x之间的函数关系式为y=,当它的长为25米时,它的宽为________________.2-1-c-n-j-y
5.一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示.当0≤x≤1时,y关于x的函数表达式为y=60x,那么当1
(1)A比B后出发几小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
培优提升
1.设等腰三角形顶角的度数为y度,底角的度数为x度,则有( )
A.y=180-2x(x为全体实数)
B.y=180-2x(0≤x≤90)
C.y=180-2x(0
A.I= B.I=
C.I= D.I=-
3.如图,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )21·世纪*教育网
4.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶.已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示,以下说法错误的是( )www-2-1-cnjy-com
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=-8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还余油6升
5.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s,在跑步过程中,甲、乙两人间的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123,其中正确的是( )【来源:21·世纪·教育·网】
A.①②③ B.①② C.①③ D.②③
6.某天,为按计划准点到达某个海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是 .21世纪教育网版权所有
7.新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.21*cnjy*com
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
参考答案
【基础训练】
1.【答案】D 2.【答案】A
3.【答案】B 4.【答案】8米
5.【答案】y=100x-40
解:∵当0≤x≤1时,y关于x的函数表达式为y=60x,∴当x=1时,y=60.又∵当x=2时,y=160,∴当1
(2)设直线DE对应的函数表达式为s=kt+b.
把D(1,0),E(3,90)的坐标分别代入得解得
∴直线DE对应的函数表达式为s=45t-45.
∵直线OC对应的函数表达式为s=20t.
由解得
∴在B出发后1.8 h,两人相遇.
【培优提升】
1.【答案】C
解:根据三角形内角和为180° 得y+2x=180,变形得y=180-2x,自变量x的取值范围为0
4.【答案】C
解:A.设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b,
将(0,25),(2,9)代入,得解得
所以y=-8t+25,正确,故本选项不符合题意;B.由函数图象可知,途中加油30-9=21(升),正确,故本选项不符合题意;C.由函数图象可知,汽车每小时用油(25-9)÷2=8(升),所以汽车加油后还可行驶30÷8=3(小时),3<4,错误,故本选项符合题意;D.汽车从甲地到达乙地,所需时间为500÷100=5(小时),5小时耗油量为8×5=40(升),∵汽车出发前油箱有油25升,途中加油21升,∴汽车到达乙地时油箱中还余油25+21-40=6(升),正确,故本选项不符合题意.故选C.
5.【答案】A
解:乙出发时甲跑了2 s,相距8 m,所以甲的速度为4 m/s.100 s后乙开始休息,所以乙的速度是500÷100=5(m/s).a s后甲、乙相遇,所以a==8,故①正确.100 s后乙到达终点,甲跑了4×(100+2)=408(m),所以b=500-408=92,故②正确.甲到达终点一共用时500÷4=125(s),所以c=125-2=123.故③正确.故选A.【出处:21教育名师】
6.【答案】7:00
解:由函数图象及题意,得故障前的速度为80÷1=80(海里/小时),故障后的速度为(180-80)÷1=100(海里/小时).设全程长为a海里,由题意,得=2+,解得a=480,21教育网
则原计划行驶的时间为480÷80=6(小时),
故原计划准点到达的时刻为7:00.
7.解:(1)当1≤x≤8时,y=4000-30(8-x)=4000-240+30x=30x+3760;
当8
y=
(2)当x=16时,
方案一每套楼房总费用:
w1=120(50×16+3600)×92%-a=485760-a;
方案二每套楼房总费用:
w2=120(50×16+3600)×90%=475200.
∴当w1
当w1=w2时,即485760-a=475 200时,a=10560;
当w1>w2时,即485760-a>475 200时,a<10560.
因此,当每套赠送的装修基金多于10560元时,选择方案一合算;
当每套赠送的装修基金等于10560元时,两种方案一样;
当每套赠送的装修基金少于10560元时,选择方案二合算.
