17.5.3 一次函数与二元一次方程(组)的关系 同步练习
文档属性
| 名称 | 17.5.3 一次函数与二元一次方程(组)的关系 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 589.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 21:57:48 | ||
图片预览



文档简介
17.5.3 一次函数与二元一次方程(组)的关系
核心笔记: 1.一次函数与二元一次方程的关系:一般地,一次函数y=kx+b的图象上任意一点的坐标都是二元一次方程kx-y+b=0的解;以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.21教育网
2.两个一次函数与二元一次方程组的解的关系:一般地,如果两个一次函数的图象有一个交点,那么交点的坐标就是相应的二元一次方程组的解.所以解二元一次方程组还可以用图象法求解.21·世纪*教育网
3.用图象法解二元一次方程组的步骤
(1)把二元一次方程化成一次函数的形式;
(2)在平面直角坐标系中画出两个一次函数的图象,并标出交点,交点坐标就是方程组的解.
基础训练
1.既在直线y=3x+2上,又在直线y=2x+4上的点是( )
A.(-2,4) B.(-2,-4)
C.(2,8) D.(2,-8)
2.如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解是( )2-1-c-n-j-y
A. B.
C. D.
3.用图象法解方程组时,图中正确的是( )
4.已知二元一次方程组的解为则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=-x-1的交点坐标为 .?21世纪教育网版权所有
5.直线y=x+3是由直线y=x-1沿y轴向________平移________个单位得到的,由此可知方程组的解的情况为________.?
6.如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x的图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积.
培优提升
1.在同一平面直角坐标系中,若一次函数y=-x+3与y=3x-5的图象交于点M,则点M的坐标为( )www-2-1-cnjy-com
A.(-1,4) B.(-1,2) C.(2,-1) D.(2,1)
2.已知直线l1:(m-2)x-y=3和l2:x-y=3与直线l3:2x-y=2相交于同一点,则m=( ) 21cnjy.com
A.1 B.3 C.4 D.-3
3.显然方程组没有解,因此一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行 C.相交 D.无法判断
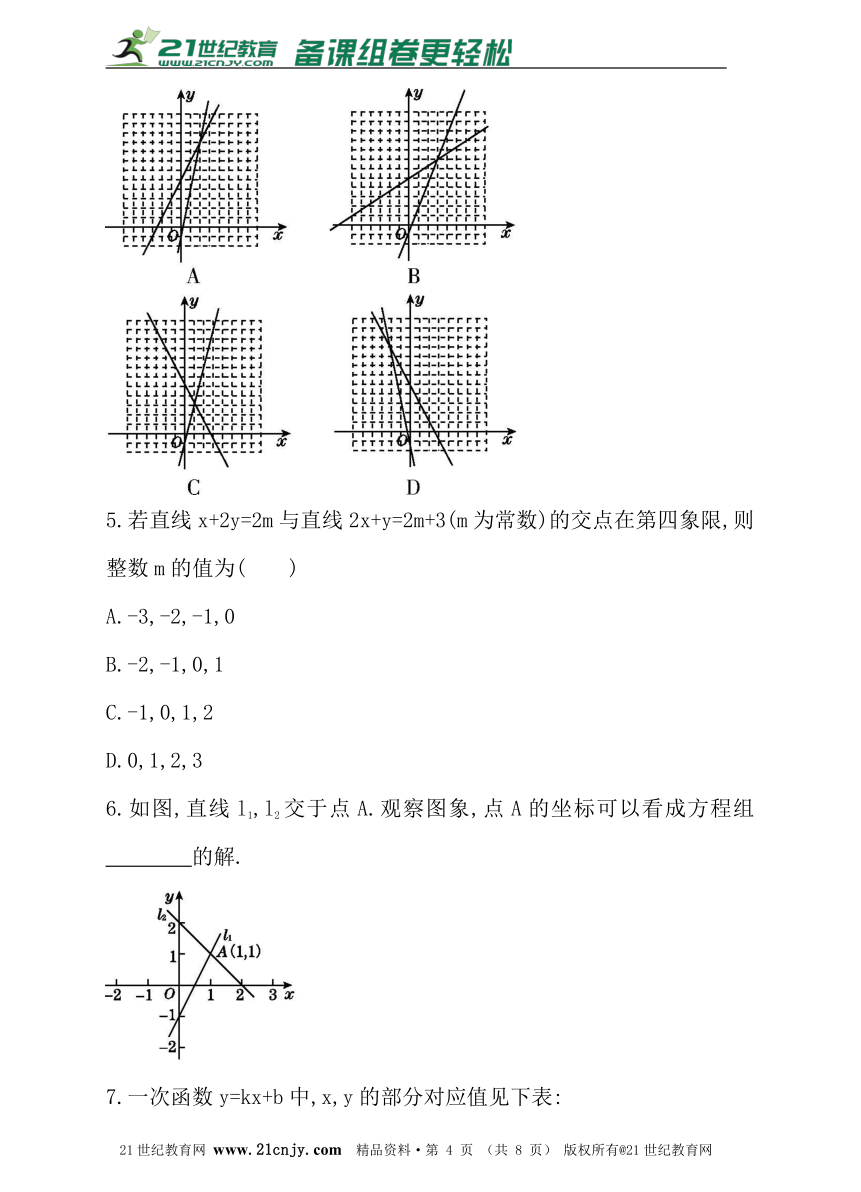
4.下列各个选项中的网格都是由边长为1的小正方形组成的,利用函数的图象解方程5x-1=2x+5,其中正确的是( )21*cnjy*com
5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为( )21·cn·jy·com
A.-3,-2,-1,0
B.-2,-1,0,1
C.-1,0,1,2
D.0,1,2,3
6.如图,直线l1,l2交于点A.观察图象,点A的坐标可以看成方程组________的解.
7.一次函数y=kx+b中,x,y的部分对应值见下表:
x
…
-1
0
1
2
3
…
y
…
-7
-4
-1
2
5
…
正比例函数的关系式为y=x,则方程组的解为
x=_____________,y=____________.?
8.如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象交于点A.
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交函数y=x和y=-x+7的图象于点B,C,连结OC,若BC=OA,求△OBC的面积.www.21-cn-jy.com
9.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1,y2关于x的函数图象如图所示.
(1)根据图象,直接写出y1,y2关于x的函数关系式;
(2)若两车之间的距离为s千米,请写出s关于x的函数关系式.
参考答案
【基础训练】
1.【答案】C 2.【答案】A 3.【答案】C 4.【答案】(-4,1)
5.【答案】上;4;无解
6.解:将P(2,n)的坐标代入y=x得,n=3.
故P点坐标为(2,3),将P(2,3)的坐标代入y=-x+m得
3=-2+m,m=5 ,∴m=5,n=3.
(2)在一次函数y=-x+5中,令x=0得y=5,
∴B点坐标为(0,5).
∴S△POB=×5×2=5.
【培优提升】
1.【答案】D
解:联立
解得所以点M的坐标为(2,1).
2.【答案】B
解:求出直线l2与l3的交点坐标为(-1,-4),然后把交点坐标代入(m-2)x-y=3,即可求出m的值.2·1·c·n·j·y
3.【答案】B 4.【答案】A
5.【答案】B
解:由题意得解得
∴交点坐标为.∵交点在第四象限,∴解得-36.【答案】
7.【答案】2;2
8.解:(1)由题意得解得∴点A的坐标为(4,3).
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理,
得OA===5,∴BC=OA=×5=7.∵P(a,0),∴B,C(a,-a+7),∴BC=a-(-a+7)=a-7,∴a-7=7,解得a=8.
∴S△OBC=BC·OP=×7×8=28.
9.解:(1)y1=60x(0≤x≤10),y2=600-100x(0≤x≤6).
(2)当y1=y2时,60x=600-100x,x=,即两车行驶小时相遇.
相遇前:s=y2-y1=600-100x-60x=600-160x.
相遇后且出租车到达甲地
前:s=y1-y2=60x-(600-100x)=160x-600.
出租车到达甲地后:s=60x(6≤x≤10).
综上,s=
核心笔记: 1.一次函数与二元一次方程的关系:一般地,一次函数y=kx+b的图象上任意一点的坐标都是二元一次方程kx-y+b=0的解;以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.21教育网
2.两个一次函数与二元一次方程组的解的关系:一般地,如果两个一次函数的图象有一个交点,那么交点的坐标就是相应的二元一次方程组的解.所以解二元一次方程组还可以用图象法求解.21·世纪*教育网
3.用图象法解二元一次方程组的步骤
(1)把二元一次方程化成一次函数的形式;
(2)在平面直角坐标系中画出两个一次函数的图象,并标出交点,交点坐标就是方程组的解.
基础训练
1.既在直线y=3x+2上,又在直线y=2x+4上的点是( )
A.(-2,4) B.(-2,-4)
C.(2,8) D.(2,-8)
2.如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解是( )2-1-c-n-j-y
A. B.
C. D.
3.用图象法解方程组时,图中正确的是( )
4.已知二元一次方程组的解为则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=-x-1的交点坐标为 .?21世纪教育网版权所有
5.直线y=x+3是由直线y=x-1沿y轴向________平移________个单位得到的,由此可知方程组的解的情况为________.?
6.如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x的图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积.
培优提升
1.在同一平面直角坐标系中,若一次函数y=-x+3与y=3x-5的图象交于点M,则点M的坐标为( )www-2-1-cnjy-com
A.(-1,4) B.(-1,2) C.(2,-1) D.(2,1)
2.已知直线l1:(m-2)x-y=3和l2:x-y=3与直线l3:2x-y=2相交于同一点,则m=( ) 21cnjy.com
A.1 B.3 C.4 D.-3
3.显然方程组没有解,因此一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行 C.相交 D.无法判断
4.下列各个选项中的网格都是由边长为1的小正方形组成的,利用函数的图象解方程5x-1=2x+5,其中正确的是( )21*cnjy*com
5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为( )21·cn·jy·com
A.-3,-2,-1,0
B.-2,-1,0,1
C.-1,0,1,2
D.0,1,2,3
6.如图,直线l1,l2交于点A.观察图象,点A的坐标可以看成方程组________的解.
7.一次函数y=kx+b中,x,y的部分对应值见下表:
x
…
-1
0
1
2
3
…
y
…
-7
-4
-1
2
5
…
正比例函数的关系式为y=x,则方程组的解为
x=_____________,y=____________.?
8.如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象交于点A.
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交函数y=x和y=-x+7的图象于点B,C,连结OC,若BC=OA,求△OBC的面积.www.21-cn-jy.com
9.一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1,y2关于x的函数图象如图所示.
(1)根据图象,直接写出y1,y2关于x的函数关系式;
(2)若两车之间的距离为s千米,请写出s关于x的函数关系式.
参考答案
【基础训练】
1.【答案】C 2.【答案】A 3.【答案】C 4.【答案】(-4,1)
5.【答案】上;4;无解
6.解:将P(2,n)的坐标代入y=x得,n=3.
故P点坐标为(2,3),将P(2,3)的坐标代入y=-x+m得
3=-2+m,m=5 ,∴m=5,n=3.
(2)在一次函数y=-x+5中,令x=0得y=5,
∴B点坐标为(0,5).
∴S△POB=×5×2=5.
【培优提升】
1.【答案】D
解:联立
解得所以点M的坐标为(2,1).
2.【答案】B
解:求出直线l2与l3的交点坐标为(-1,-4),然后把交点坐标代入(m-2)x-y=3,即可求出m的值.2·1·c·n·j·y
3.【答案】B 4.【答案】A
5.【答案】B
解:由题意得解得
∴交点坐标为.∵交点在第四象限,∴解得-3
7.【答案】2;2
8.解:(1)由题意得解得∴点A的坐标为(4,3).
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理,
得OA===5,∴BC=OA=×5=7.∵P(a,0),∴B,C(a,-a+7),∴BC=a-(-a+7)=a-7,∴a-7=7,解得a=8.
∴S△OBC=BC·OP=×7×8=28.
9.解:(1)y1=60x(0≤x≤10),y2=600-100x(0≤x≤6).
(2)当y1=y2时,60x=600-100x,x=,即两车行驶小时相遇.
相遇前:s=y2-y1=600-100x-60x=600-160x.
相遇后且出租车到达甲地
前:s=y1-y2=60x-(600-100x)=160x-600.
出租车到达甲地后:s=60x(6≤x≤10).
综上,s=
