18.1.1 平行四边形的边、角性质 同步练习
文档属性
| 名称 | 18.1.1 平行四边形的边、角性质 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 436.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 00:00:00 | ||
图片预览



文档简介
18.1.1 平行四边形的边、角性质
核心笔记: 1.平行四边形:有两组对边分别平行的四边形叫做平行四边形. 平行四边形是中心对称图形,对称中心是两条对角线的交点.
2.平行四边形边的性质:平行四边形的对边平行且相等.
3.平行四边形角的性质:平行四边形的对角相等.
4. 两条平行线间的距离:两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.平行线之间的距离处处相等.【来源:21cnj*y.co*m】
基础训练
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )【版权所有:21教育】
A.12个 B.9个
C.7个 D.5个
2.已知?ABCD的周长为32,AB=4,则BC=( )
A.4 B.12 C.24 D.28
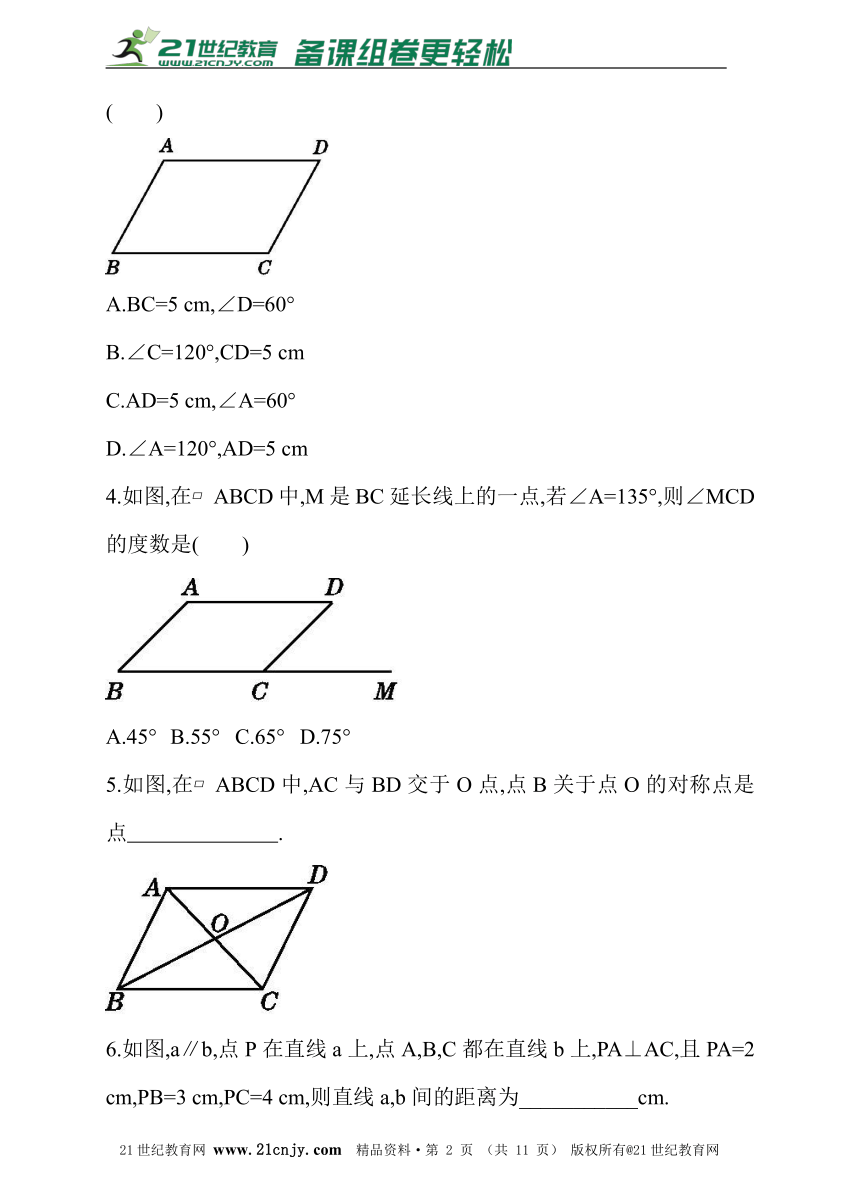
3.如图,在平行四边形ABCD中,∠B=60°,AB=5cm,则下面结论正确的是( )
A.BC=5 cm,∠D=60°
B.∠C=120°,CD=5 cm
C.AD=5 cm,∠A=60°
D.∠A=120°,AD=5 cm
4.如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65° D.75°
5.如图,在?ABCD中,AC与BD交于O点,点B关于点O的对称点是点 .?
6.如图,a∥b,点P在直线a上,点A,B,C都在直线b上,PA⊥AC,且PA=2 cm,PB=3 cm,PC=4 cm,则直线a,b间的距离为___________cm.?
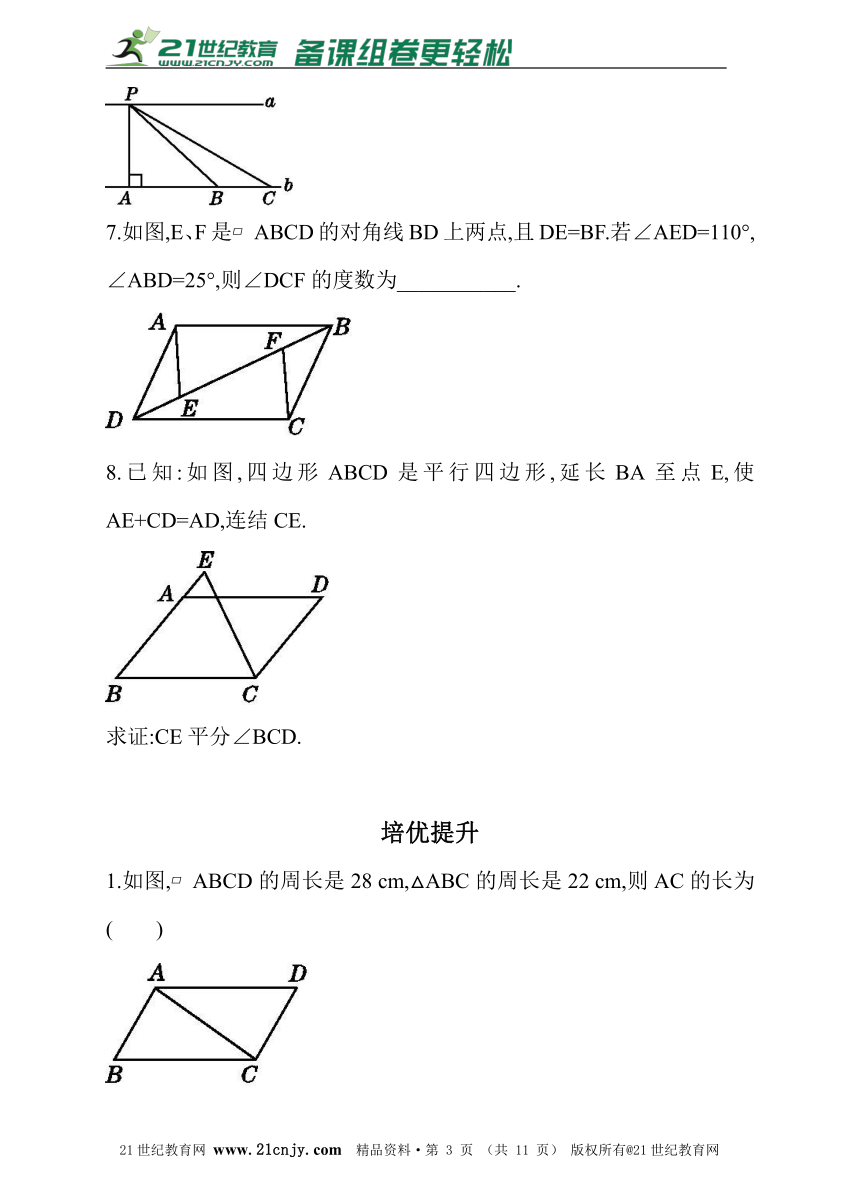
7.如图,E、F是?ABCD的对角线BD上两点,且DE=BF.若∠AED=110°,∠ABD=25°,则∠DCF的度数为___________.?21·世纪*教育网
8.已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD,连结CE.
求证:CE平分∠BCD.
培优提升
1.如图,?ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为( )
A.6 cm B.12 cm C.4 cm D.8 cm
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出( )个形状不同的平行四边形.21世纪教育网版权所有
A.1 B.2 C.3 D.4
3.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18° B.36° C.72° D.144°
4.如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F=( )21教育网
A.110° B.30° C.50° D.70°
5.已知:如图,在平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则AE=________,EF=________,BE与CF的位置关系是________. 21*cnjy*com
6.在?ABCD中,∠DAB的平分线分边BC为6 cm和5 cm两部分,则?ABCD的周长为 . 【出处:21教育名师】
7.如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则△ACE的面积为 .?21教育名师原创作品
8.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是 .?
9.?ABCD的周长为30 cm,两邻边的长度之比为2∶3(ABAB= cm,BC= cm.?
10.如图,在?ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连结CE.试判断CE和DF的位置关系,并说明理由.
11.如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证:∠EDB=∠EBD;
(2)判断AF与DB是否平行,并说明理由.
12.如图,平面直角坐标系中有一个5×5的方阵,在方阵中横、纵坐标都是整数的点叫格点,四个点都是格点的四边形叫格点四边形,已知A(1,2),B(3,2).以A、B为顶点,面积为2的格点平行四边形的个数是( ) 21cnjy.com
A.9个 B.10个 C.11个 D.13个
参考答案
【基础训练】
1.【答案】B
2.【答案】B
解:根据平行四边形的性质得到AB=CD,AD=BC,根据2(AB+BC)=32,即可求出答案.
3.【答案】B
解:根据已知条件,结合平行四边形的性质,逐个分析各选项,即可选出正确答案.
4.【答案】A
解:由?ABCD,可知∠A=∠BCD,而∠BCD+∠MCD=180°,所以∠MCD=45°.
5.【答案】D
解:平行四边形是中心对称图形,其对称中心为对角线的交点.
6.【答案】2
7.【答案】85°
解:首先由BF=DE可以得到BE=DF,然后利用平行四边形的性质可以得到AB=CD,AB∥CD,接着可以得到∠ABD=∠CDB,利用全等三角形的判定方法即可得到△ABE≌△CDF,从而得到∠DFC=∠AEB,再根据条件∠AED=110°,求出∠DFC=∠AEB=70°后,即可根据三角形内角和为180°求得答案.21·cn·jy·com
8.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∴∠E=∠DCE.
∵AE+CD=AD,
∴BE=BC,
∴∠E=∠BCE,
∴∠DCE=∠BCE,
即CE平分∠BCD.
【培优提升】
1.【答案】D
解:根据平行四边形对边相等的性质可知?ABCD的周长=2(AB+BC).又△ABC的周长=AB+BC+AC,故www.21-cn-jy.com
2AC=2(AB+BC+AC)-2(AB+BC)=△ABC的周长×2-?ABCD的周长,代值求解.
2.【答案】C
3.【答案】B
解:根据平行四边形的性质可知∠C=∠A,由BC∥AD,得∠A+∠B=180°,求出∠A的度数,即可求出∠C的度数.【来源:21·世纪·教育·网】
4.【答案】D
解:要求∠E+∠F的度数,只需求出∠ADE的度数,而∠ADE=∠A,∠A与∠B互补,所以可以先求出∠A的度数,进而求解问题.
5.【答案】3;1;BE⊥CF
解:根据平行四边形的性质可知AD∥BC,则∠DFC=∠FCB.又因为CF平分∠BCD,所以∠DCF=∠FCB,则∠DFC=∠DCF,所以DF=DC=AB=3.同理可得AE=3,所以DE=AF=5-3=2,根据AF+EF+ED=AD=5,可求得EF=1.www-2-1-cnjy-com
6.【答案】32 cm或34 cm
解:由题意可得AB=6 cm或AB=5 cm.
7.【答案】8
解:根据两平行线间的距离处处相等,可知两个三角形的高相等,所以根据△ABD的面积可求出△ACE的高,然后求其面积即可.
8.【答案】(7,3)
解:因为CD∥AB,所以C点的纵坐标与D点的纵坐标相同,为3.又因为AB=CD=5,故可得C点横坐标为7.故答案为(7,3).2·1·c·n·j·y
9.【答案】6;9
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD.
又∵两邻边的长度之比为2∶3(AB依题意可列方程2x+3x+2x+3x=30,解得x=3,
∴2x=2×3=6,3x=3×3=9.
∴AB=6 cm,BC=9 cm.
10.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADE=∠CFE.∵点E是AB边的中点,∴AE=BE.又∵∠AED=∠BEF,∴△ADE≌△BFE.2-1-c-n-j-y
(2)解:CE⊥DF且CE平分DF,理由如下:
∵DF平分∠ADC,∴∠ADF=∠CDF.又∵AD∥BC,∴∠ADF=∠CFE,∴∠CDF=∠CFE,∴CD=CF.由(1)知△ADE≌△BFE,∴DE=EF,即点E为DF的中点,∴CE⊥DF且CE平分DF.21*cnjy*com
11.(1)证明:由折叠可知∠CDB=∠EDB.
∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDB=∠EBD,
∴∠EDB=∠EBD.
(2)解:AF∥DB.
理由:∵∠EDB=∠EBD,∴DE=BE.
由折叠可知DC=DF.∵四边形ABCD是平行四边形,∴DC=AB,∴DF=AB,∴AE=EF,
∴∠EAF=∠EFA.
在△BED中,∠EDB+∠EBD+∠DEB=180°,
即2∠EDB+∠DEB=180°.
同理在△AEF中,2∠EFA+∠AEF=180°.
∵∠DEB=∠AEF,∴∠EDB=∠EFA,
∴AF∥DB.
12.【答案】D
核心笔记: 1.平行四边形:有两组对边分别平行的四边形叫做平行四边形. 平行四边形是中心对称图形,对称中心是两条对角线的交点.
2.平行四边形边的性质:平行四边形的对边平行且相等.
3.平行四边形角的性质:平行四边形的对角相等.
4. 两条平行线间的距离:两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.平行线之间的距离处处相等.【来源:21cnj*y.co*m】
基础训练
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,EF与HN相交于点O,则图中共有平行四边形( )【版权所有:21教育】
A.12个 B.9个
C.7个 D.5个
2.已知?ABCD的周长为32,AB=4,则BC=( )
A.4 B.12 C.24 D.28
3.如图,在平行四边形ABCD中,∠B=60°,AB=5cm,则下面结论正确的是( )
A.BC=5 cm,∠D=60°
B.∠C=120°,CD=5 cm
C.AD=5 cm,∠A=60°
D.∠A=120°,AD=5 cm
4.如图,在?ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65° D.75°
5.如图,在?ABCD中,AC与BD交于O点,点B关于点O的对称点是点 .?
6.如图,a∥b,点P在直线a上,点A,B,C都在直线b上,PA⊥AC,且PA=2 cm,PB=3 cm,PC=4 cm,则直线a,b间的距离为___________cm.?
7.如图,E、F是?ABCD的对角线BD上两点,且DE=BF.若∠AED=110°,∠ABD=25°,则∠DCF的度数为___________.?21·世纪*教育网
8.已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE+CD=AD,连结CE.
求证:CE平分∠BCD.
培优提升
1.如图,?ABCD的周长是28 cm,△ABC的周长是22 cm,则AC的长为( )
A.6 cm B.12 cm C.4 cm D.8 cm
2.以长为5,4,7的三条线段中的两条为边,另一条为对角线画平行四边形,可以画出( )个形状不同的平行四边形.21世纪教育网版权所有
A.1 B.2 C.3 D.4
3.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18° B.36° C.72° D.144°
4.如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连结EF,则∠E+∠F=( )21教育网
A.110° B.30° C.50° D.70°
5.已知:如图,在平行四边形ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F,若AB=3,BC=5,则AE=________,EF=________,BE与CF的位置关系是________. 21*cnjy*com
6.在?ABCD中,∠DAB的平分线分边BC为6 cm和5 cm两部分,则?ABCD的周长为 . 【出处:21教育名师】
7.如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则△ACE的面积为 .?21教育名师原创作品
8.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是 .?
9.?ABCD的周长为30 cm,两邻边的长度之比为2∶3(AB
10.如图,在?ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连结CE.试判断CE和DF的位置关系,并说明理由.
11.如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证:∠EDB=∠EBD;
(2)判断AF与DB是否平行,并说明理由.
12.如图,平面直角坐标系中有一个5×5的方阵,在方阵中横、纵坐标都是整数的点叫格点,四个点都是格点的四边形叫格点四边形,已知A(1,2),B(3,2).以A、B为顶点,面积为2的格点平行四边形的个数是( ) 21cnjy.com
A.9个 B.10个 C.11个 D.13个
参考答案
【基础训练】
1.【答案】B
2.【答案】B
解:根据平行四边形的性质得到AB=CD,AD=BC,根据2(AB+BC)=32,即可求出答案.
3.【答案】B
解:根据已知条件,结合平行四边形的性质,逐个分析各选项,即可选出正确答案.
4.【答案】A
解:由?ABCD,可知∠A=∠BCD,而∠BCD+∠MCD=180°,所以∠MCD=45°.
5.【答案】D
解:平行四边形是中心对称图形,其对称中心为对角线的交点.
6.【答案】2
7.【答案】85°
解:首先由BF=DE可以得到BE=DF,然后利用平行四边形的性质可以得到AB=CD,AB∥CD,接着可以得到∠ABD=∠CDB,利用全等三角形的判定方法即可得到△ABE≌△CDF,从而得到∠DFC=∠AEB,再根据条件∠AED=110°,求出∠DFC=∠AEB=70°后,即可根据三角形内角和为180°求得答案.21·cn·jy·com
8.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD=BC,
∴∠E=∠DCE.
∵AE+CD=AD,
∴BE=BC,
∴∠E=∠BCE,
∴∠DCE=∠BCE,
即CE平分∠BCD.
【培优提升】
1.【答案】D
解:根据平行四边形对边相等的性质可知?ABCD的周长=2(AB+BC).又△ABC的周长=AB+BC+AC,故www.21-cn-jy.com
2AC=2(AB+BC+AC)-2(AB+BC)=△ABC的周长×2-?ABCD的周长,代值求解.
2.【答案】C
3.【答案】B
解:根据平行四边形的性质可知∠C=∠A,由BC∥AD,得∠A+∠B=180°,求出∠A的度数,即可求出∠C的度数.【来源:21·世纪·教育·网】
4.【答案】D
解:要求∠E+∠F的度数,只需求出∠ADE的度数,而∠ADE=∠A,∠A与∠B互补,所以可以先求出∠A的度数,进而求解问题.
5.【答案】3;1;BE⊥CF
解:根据平行四边形的性质可知AD∥BC,则∠DFC=∠FCB.又因为CF平分∠BCD,所以∠DCF=∠FCB,则∠DFC=∠DCF,所以DF=DC=AB=3.同理可得AE=3,所以DE=AF=5-3=2,根据AF+EF+ED=AD=5,可求得EF=1.www-2-1-cnjy-com
6.【答案】32 cm或34 cm
解:由题意可得AB=6 cm或AB=5 cm.
7.【答案】8
解:根据两平行线间的距离处处相等,可知两个三角形的高相等,所以根据△ABD的面积可求出△ACE的高,然后求其面积即可.
8.【答案】(7,3)
解:因为CD∥AB,所以C点的纵坐标与D点的纵坐标相同,为3.又因为AB=CD=5,故可得C点横坐标为7.故答案为(7,3).2·1·c·n·j·y
9.【答案】6;9
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD.
又∵两邻边的长度之比为2∶3(AB
∴2x=2×3=6,3x=3×3=9.
∴AB=6 cm,BC=9 cm.
10.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADE=∠CFE.∵点E是AB边的中点,∴AE=BE.又∵∠AED=∠BEF,∴△ADE≌△BFE.2-1-c-n-j-y
(2)解:CE⊥DF且CE平分DF,理由如下:
∵DF平分∠ADC,∴∠ADF=∠CDF.又∵AD∥BC,∴∠ADF=∠CFE,∴∠CDF=∠CFE,∴CD=CF.由(1)知△ADE≌△BFE,∴DE=EF,即点E为DF的中点,∴CE⊥DF且CE平分DF.21*cnjy*com
11.(1)证明:由折叠可知∠CDB=∠EDB.
∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDB=∠EBD,
∴∠EDB=∠EBD.
(2)解:AF∥DB.
理由:∵∠EDB=∠EBD,∴DE=BE.
由折叠可知DC=DF.∵四边形ABCD是平行四边形,∴DC=AB,∴DF=AB,∴AE=EF,
∴∠EAF=∠EFA.
在△BED中,∠EDB+∠EBD+∠DEB=180°,
即2∠EDB+∠DEB=180°.
同理在△AEF中,2∠EFA+∠AEF=180°.
∵∠DEB=∠AEF,∴∠EDB=∠EFA,
∴AF∥DB.
12.【答案】D
