18.1.2 平行四边形的对角线性质 同步练习
文档属性
| 名称 | 18.1.2 平行四边形的对角线性质 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 515.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 00:00:00 | ||
图片预览


文档简介
18.1.2 平行四边形的对角线性质
核心笔记: 平行四边形的对角线性质:平行四边形的对角线互相平分.
基础训练
1.如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
2.平行四边形ABCD的对角线交于点O,下列结论错误的是( )
A.平行四边形ABCD是中心对称图形
B.△AOB≌△COD
C.△AOB≌△BOC
D.△AOB与△BOC的面积相等
3.如图所示,在?ABCD中,EF过对角线的交点O,如果AB=6 cm,AD=5 cm,OF=2 cm,那么四边形BCEF的周长为( )www.21-cn-jy.com
A.13 cm B.15 cm C.11 cm D.9.5 cm
4.如图,过?ABCD的对角线BD上一点M分别作平行四边形相邻两边的平行线EF与GH,那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是( )2·1·c·n·j·y
A.S1>S2 B.S1=S2 C.S15.如图,过平行四边形ABCD的对称中心O任意画5条直线a、b、m、n、l,已知BC=6,BC边上的高为4,则阴影部分的面积为( )
A.24 B.12 C.6 D.3
6.如图,在?ABCD中,O是对角线的交点,AB=13 cm,BC=5 cm,那么△AOB的周长比△BOC的周长多________cm.?【来源:21·世纪·教育·网】
7.如图,?ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
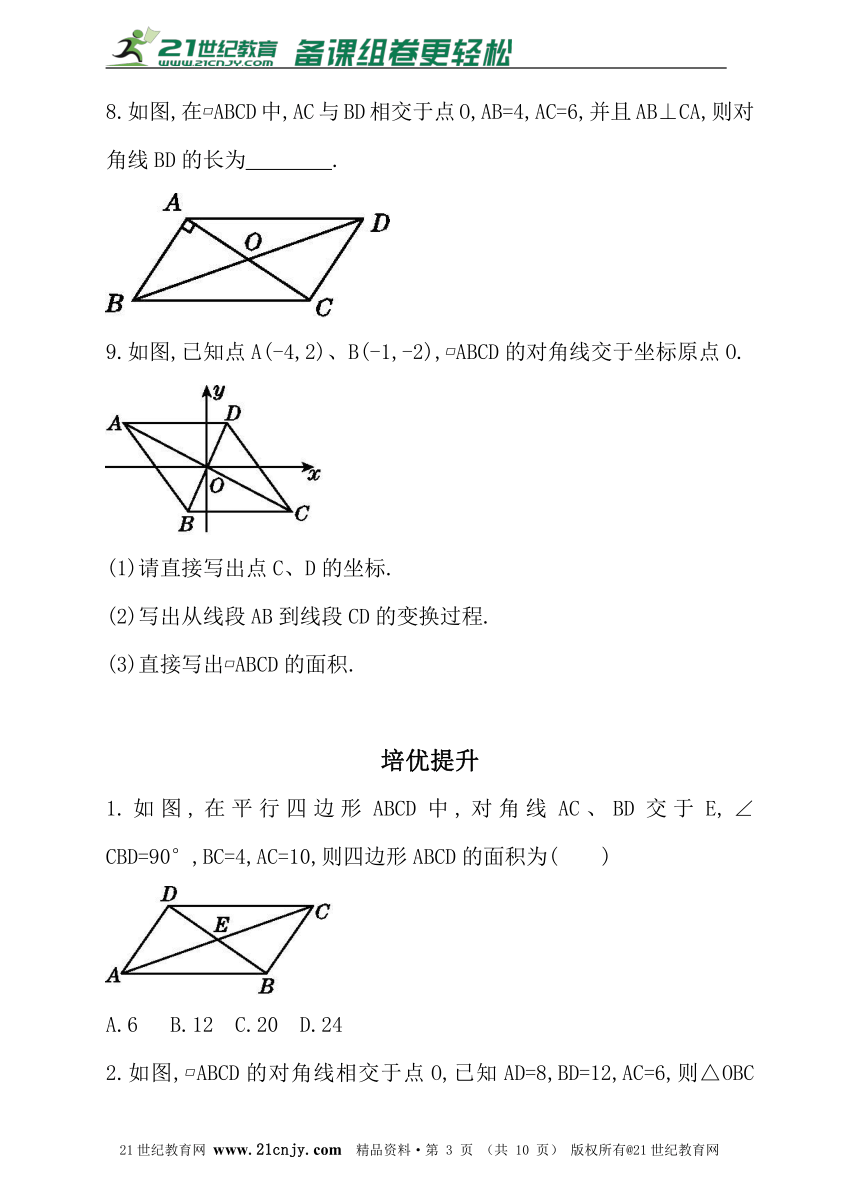
8.如图,在?ABCD中,AC与BD相交于点O,AB=4,AC=6,并且AB⊥CA,则对角线BD的长为 .21·世纪*教育网
9.如图,已知点A(-4,2)、B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C、D的坐标.
(2)写出从线段AB到线段CD的变换过程.
(3)直接写出?ABCD的面积.
培优提升
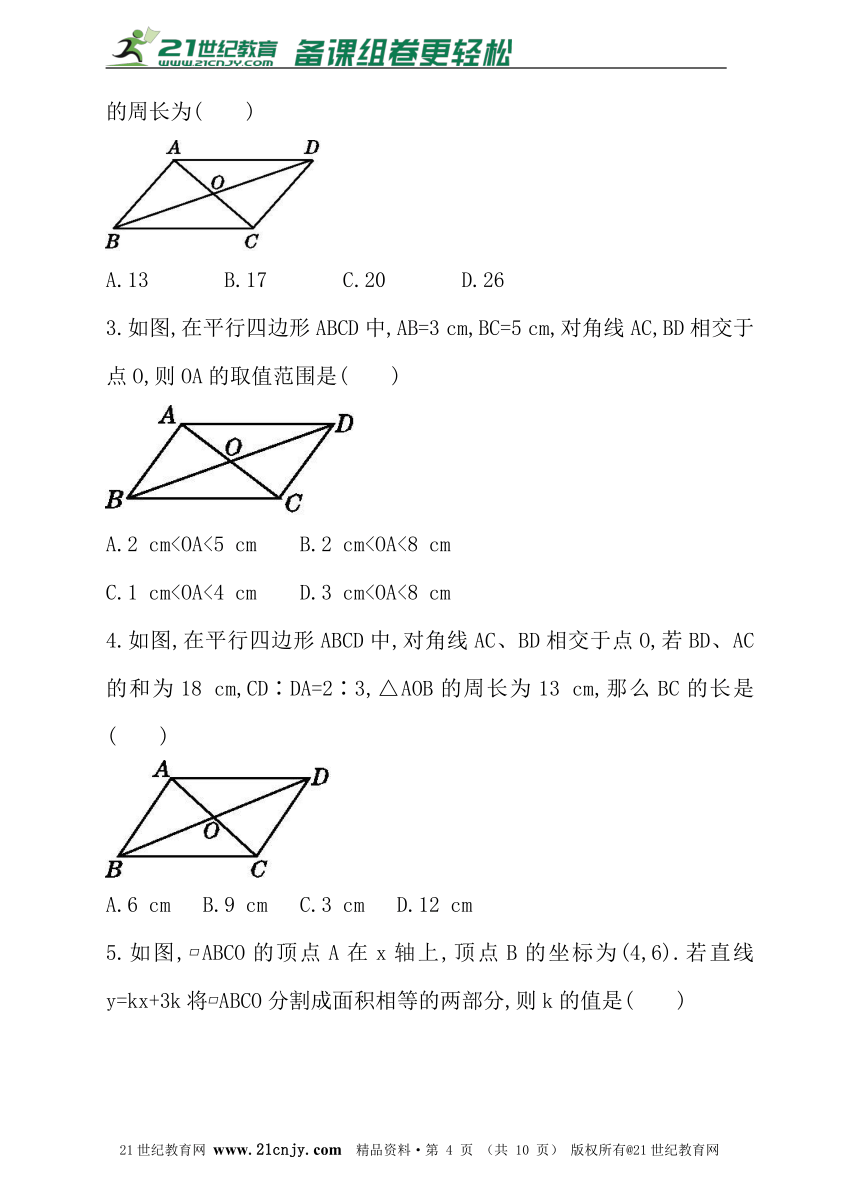
1.如图,在平行四边形ABCD中,对角线AC、BD交于E,∠CBD=90°,BC=4,AC=10,则四边形ABCD的面积为( )
A.6 B.12 C.20 D.24
2.如图,?ABCD的对角线相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21·cn·jy·com
A.13 B.17 C.20 D.26
3.如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( ) www-2-1-cnjy-com
A.2 cmC.1 cm4.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若BD、AC的和为18 cm,CD∶DA=2∶3,△AOB的周长为13 cm,那么BC的长是( )2-1-c-n-j-y
A.6 cm B.9 cm C.3 cm D.12 cm
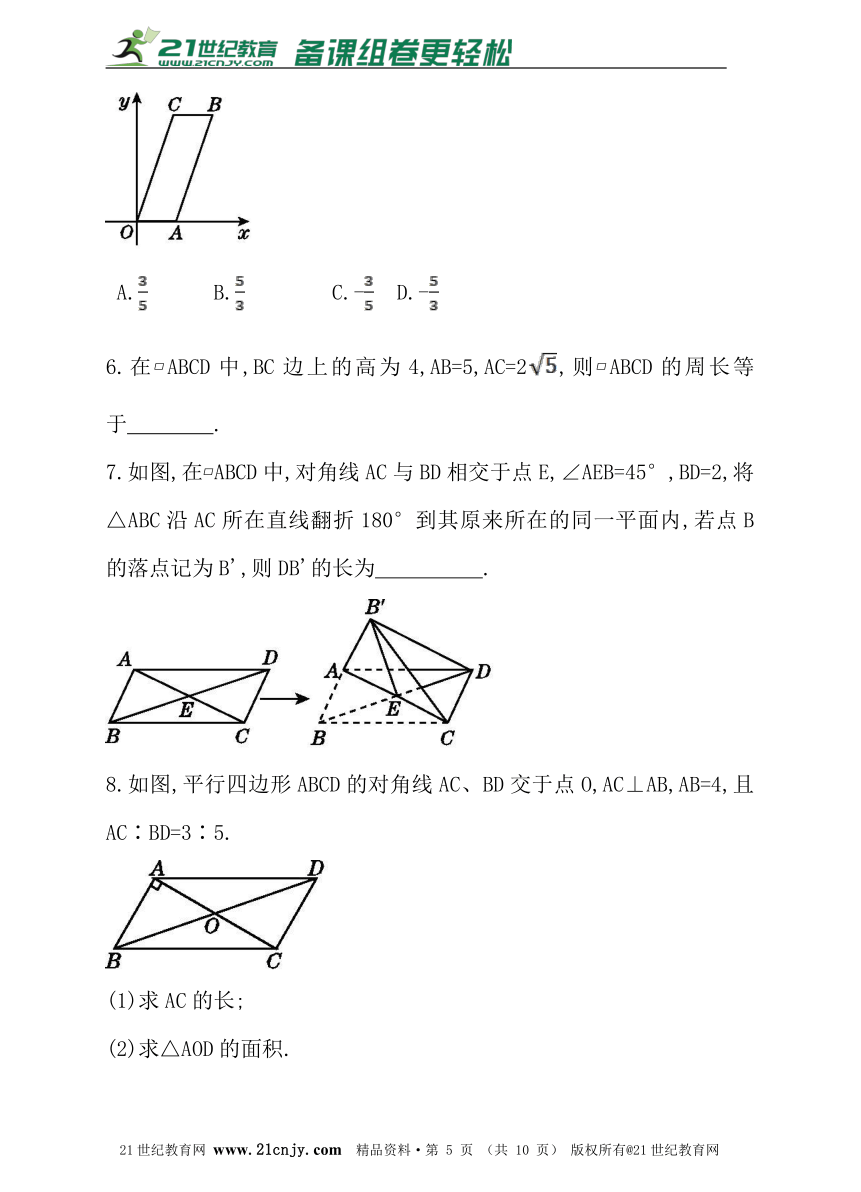
5.如图,?ABCO的顶点A在x轴上,顶点B的坐标为(4,6).若直线y=kx+3k将?ABCO分割成面积相等的两部分,则k的值是( )
A. B. C.- D.-
6.在?ABCD中,BC边上的高为4,AB=5,AC=2,则?ABCD的周长等于 .
7.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B',则DB'的长为 .21*cnjy*com
8.如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=4,且AC∶BD=3∶5.【来源:21cnj*y.co*m】
(1)求AC的长;
(2)求△AOD的面积.
9.如图①,已知?ABCD的周长为6,AB=1,对角线AC与BD相交于点O.
(1)求这个平行四边形其余各边长;
(2)若AB⊥AC,求OC的长;
(3)将射线OA绕点O顺时针旋转得到OA',OA'交AD于E(如图②),连结CE,当旋转角度为多少时,CA平分∠BCE?说明理由.21教育网
参考答案
【基础训练】
1.【答案】C
2.【答案】C
解:A.根据平行四边形的对角线互相平分,知平行四边形是中心对称图形,结论正确.B.根据平行四边形的对角线互相平分,再结合对顶角相等,得△AOB≌△COD,结论正确.C.△AOB与△BOC不一定全等,故结论错误.D.根据平行四边形的对角线互相平分,再结合三角形的面积计算公式知结论正确.故选C.【出处:21教育名师】
3.【答案】B
解:由四边形ABCD是平行四边形,易证得△AFO≌△CEO,即可得EF=2OF,AF=CE,然后由AB=6 cm,AD=5 cm,OF=2 cm,即可求得四边形BCEF的周长.【版权所有:21教育】
4.【答案】B
5.【答案】B
解:∵O为对称中心,∴阴影部分与非阴影部分的面积相等,为整个平行四边形面积的一半,∴阴影部分的面积为×4×6=12,故选B.
6.【答案】8
解:∵四边形ABCD为平行四边形,∴OA=OC.
△AOB的周长为OA+OB+AB;△BOC的周长为OB+OC+BC.
∴两三角形的周长之差为OA+OB+AB-(OB+OC+BC)=AB-BC=13-5=8(cm).
7.【答案】1解:∵四边形ABCD是平行四边形,
∴OA=AC=4,OD=BD=3,
在△AOD中,由三角形的三边关系得4-38.【答案】10
解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵AC=6,∴OA=AC=3.又∵AB⊥CA,∴△BAO是直角三角形.∵AB=4,OA=3,∴在Rt△BAO中,由勾股定理,得OB===5,∴BD=2OB=10.
9.解:(1)点C的坐标为(4,-2),点D的坐标为(1,2).
(2)从线段AB到线段CD的变换过程是:绕点O旋转180°.(答案不唯一)
(3)S?ABCD=20.
【培优提升】
1.【答案】D
2.【答案】B
解:△OBC的周长=BC+OB+OC=AD+BD+AC=8+6+3=17.
3.【答案】C
解:在平行四边形ABCD中,OA=OC=AC.在△ABC中,AB=3 cm,BC=5 cm,
∴2 cm4.【答案】A
解:易得OA+OB=(AC+BD)=9 cm.又∵△AOB的周长为13 cm,∴AB=CD=4 cm.21世纪教育网版权所有
又∵CD∶DA=2∶3,∴BC=AD=6 cm,故选A.
5.【答案】A
解:连结OB、AC交于点M.
∵四边形ABCO为平行四边形,
∴OM=MB=OB,
∴点M的坐标为(2,3).
∵直线y=kx+3k将?ABCO分割成面积相等的两部分,∴该直线过点M,
∴3=2k+3k,∴k=.
故选A.
6.【答案】12或20
7.【答案】
解:∵四边形ABCD是平行四边形,BD=2,
∴BE=DE=BD=1.
根据折叠的性质知,∠AEB'=∠AEB=45°,B'E=BE=1.
∴∠B'ED=180°-45°-45°=90°.又∵B'E=DE=1,
∴DB'=.故答案是.
8.解:(1)∵AC⊥AB,∴∠BAO=90°.
∵AC∶BD=3∶5,∴设AC=3a,则BD=5a.
∵四边形ABCD是平行四边形,
∴AO=AC=a,BO=BD=a.
在Rt△BAO中,由勾股定理得42+=,解得a=2(负值舍去),∴AC=3a=6.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AO=OC,BO=DO.
在△AOD和△COB中,
∴△AOD≌△COB.
∴S△AOD=S△BOC.
由(1)知OA=3,∴OC=3.
∴S△BOC=CO·AB=×3×4=6,∴△AOD的面积是6.
9.解:(1)由题意得,AB=CD=1.又∵?ABCD的周长为6,
∴AD=BC=2.
(2)∵AB=1,BC=2,AB⊥AC,∴在Rt△ABC中,根据勾股定理得
AC==,∴OC=.
(3)当旋转角度为90°时,CA平分∠BCE.
理由:由旋转角度为90°知OE⊥AC.
∵AO=CO,∴EA=EC,
∴∠EAC=∠ECA.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAC=∠ACB,∴∠ACB=∠ECA,即CA平分∠BCE.21cnjy.com
核心笔记: 平行四边形的对角线性质:平行四边形的对角线互相平分.
基础训练
1.如图,?ABCD的对角线AC、BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
2.平行四边形ABCD的对角线交于点O,下列结论错误的是( )
A.平行四边形ABCD是中心对称图形
B.△AOB≌△COD
C.△AOB≌△BOC
D.△AOB与△BOC的面积相等
3.如图所示,在?ABCD中,EF过对角线的交点O,如果AB=6 cm,AD=5 cm,OF=2 cm,那么四边形BCEF的周长为( )www.21-cn-jy.com
A.13 cm B.15 cm C.11 cm D.9.5 cm
4.如图,过?ABCD的对角线BD上一点M分别作平行四边形相邻两边的平行线EF与GH,那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是( )2·1·c·n·j·y
A.S1>S2 B.S1=S2 C.S1
A.24 B.12 C.6 D.3
6.如图,在?ABCD中,O是对角线的交点,AB=13 cm,BC=5 cm,那么△AOB的周长比△BOC的周长多________cm.?【来源:21·世纪·教育·网】
7.如图,?ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
8.如图,在?ABCD中,AC与BD相交于点O,AB=4,AC=6,并且AB⊥CA,则对角线BD的长为 .21·世纪*教育网
9.如图,已知点A(-4,2)、B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C、D的坐标.
(2)写出从线段AB到线段CD的变换过程.
(3)直接写出?ABCD的面积.
培优提升
1.如图,在平行四边形ABCD中,对角线AC、BD交于E,∠CBD=90°,BC=4,AC=10,则四边形ABCD的面积为( )
A.6 B.12 C.20 D.24
2.如图,?ABCD的对角线相交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21·cn·jy·com
A.13 B.17 C.20 D.26
3.如图,在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( ) www-2-1-cnjy-com
A.2 cm
A.6 cm B.9 cm C.3 cm D.12 cm
5.如图,?ABCO的顶点A在x轴上,顶点B的坐标为(4,6).若直线y=kx+3k将?ABCO分割成面积相等的两部分,则k的值是( )
A. B. C.- D.-
6.在?ABCD中,BC边上的高为4,AB=5,AC=2,则?ABCD的周长等于 .
7.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B',则DB'的长为 .21*cnjy*com
8.如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=4,且AC∶BD=3∶5.【来源:21cnj*y.co*m】
(1)求AC的长;
(2)求△AOD的面积.
9.如图①,已知?ABCD的周长为6,AB=1,对角线AC与BD相交于点O.
(1)求这个平行四边形其余各边长;
(2)若AB⊥AC,求OC的长;
(3)将射线OA绕点O顺时针旋转得到OA',OA'交AD于E(如图②),连结CE,当旋转角度为多少时,CA平分∠BCE?说明理由.21教育网
参考答案
【基础训练】
1.【答案】C
2.【答案】C
解:A.根据平行四边形的对角线互相平分,知平行四边形是中心对称图形,结论正确.B.根据平行四边形的对角线互相平分,再结合对顶角相等,得△AOB≌△COD,结论正确.C.△AOB与△BOC不一定全等,故结论错误.D.根据平行四边形的对角线互相平分,再结合三角形的面积计算公式知结论正确.故选C.【出处:21教育名师】
3.【答案】B
解:由四边形ABCD是平行四边形,易证得△AFO≌△CEO,即可得EF=2OF,AF=CE,然后由AB=6 cm,AD=5 cm,OF=2 cm,即可求得四边形BCEF的周长.【版权所有:21教育】
4.【答案】B
5.【答案】B
解:∵O为对称中心,∴阴影部分与非阴影部分的面积相等,为整个平行四边形面积的一半,∴阴影部分的面积为×4×6=12,故选B.
6.【答案】8
解:∵四边形ABCD为平行四边形,∴OA=OC.
△AOB的周长为OA+OB+AB;△BOC的周长为OB+OC+BC.
∴两三角形的周长之差为OA+OB+AB-(OB+OC+BC)=AB-BC=13-5=8(cm).
7.【答案】1
∴OA=AC=4,OD=BD=3,
在△AOD中,由三角形的三边关系得4-3
解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵AC=6,∴OA=AC=3.又∵AB⊥CA,∴△BAO是直角三角形.∵AB=4,OA=3,∴在Rt△BAO中,由勾股定理,得OB===5,∴BD=2OB=10.
9.解:(1)点C的坐标为(4,-2),点D的坐标为(1,2).
(2)从线段AB到线段CD的变换过程是:绕点O旋转180°.(答案不唯一)
(3)S?ABCD=20.
【培优提升】
1.【答案】D
2.【答案】B
解:△OBC的周长=BC+OB+OC=AD+BD+AC=8+6+3=17.
3.【答案】C
解:在平行四边形ABCD中,OA=OC=AC.在△ABC中,AB=3 cm,BC=5 cm,
∴2 cm
解:易得OA+OB=(AC+BD)=9 cm.又∵△AOB的周长为13 cm,∴AB=CD=4 cm.21世纪教育网版权所有
又∵CD∶DA=2∶3,∴BC=AD=6 cm,故选A.
5.【答案】A
解:连结OB、AC交于点M.
∵四边形ABCO为平行四边形,
∴OM=MB=OB,
∴点M的坐标为(2,3).
∵直线y=kx+3k将?ABCO分割成面积相等的两部分,∴该直线过点M,
∴3=2k+3k,∴k=.
故选A.
6.【答案】12或20
7.【答案】
解:∵四边形ABCD是平行四边形,BD=2,
∴BE=DE=BD=1.
根据折叠的性质知,∠AEB'=∠AEB=45°,B'E=BE=1.
∴∠B'ED=180°-45°-45°=90°.又∵B'E=DE=1,
∴DB'=.故答案是.
8.解:(1)∵AC⊥AB,∴∠BAO=90°.
∵AC∶BD=3∶5,∴设AC=3a,则BD=5a.
∵四边形ABCD是平行四边形,
∴AO=AC=a,BO=BD=a.
在Rt△BAO中,由勾股定理得42+=,解得a=2(负值舍去),∴AC=3a=6.
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AO=OC,BO=DO.
在△AOD和△COB中,
∴△AOD≌△COB.
∴S△AOD=S△BOC.
由(1)知OA=3,∴OC=3.
∴S△BOC=CO·AB=×3×4=6,∴△AOD的面积是6.
9.解:(1)由题意得,AB=CD=1.又∵?ABCD的周长为6,
∴AD=BC=2.
(2)∵AB=1,BC=2,AB⊥AC,∴在Rt△ABC中,根据勾股定理得
AC==,∴OC=.
(3)当旋转角度为90°时,CA平分∠BCE.
理由:由旋转角度为90°知OE⊥AC.
∵AO=CO,∴EA=EC,
∴∠EAC=∠ECA.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAC=∠ACB,∴∠ACB=∠ECA,即CA平分∠BCE.21cnjy.com
