18.2.1 由“边”的关系判定平行四边形 同步练习
文档属性
| 名称 | 18.2.1 由“边”的关系判定平行四边形 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 520.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 22:15:44 | ||
图片预览




文档简介
18.2.1 由“边”的关系判定平行四边形
核心笔记: 如图,已知四边形ABCD,
判定方法
主要内容
数学语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,∴四边形ABCD是平行四边形
基础训练
1.点A,B,C,D在同一平面内且任意三点不共线,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD中任选两个作为条件,能使四边形ABCD为平行四边形的选法有( )21世纪教育网版权所有
A.6种 B.5种 C.4种 D.3种
2.在四边形ABCD中,∠A∶∠B∶∠C∶∠D的比如下,其中能判断四边形是平行四边形的是( )
A.1∶2∶3∶4 B.2∶3∶4∶5
C.3∶2∶3∶2 D.3∶3∶5∶4
3.一个四边形的四条边长依次为a,b,c,d,且满足(a-c)2+(b-d)2=0,则这个四边形一定是( )21教育网
A.正方形 B.长方形
C.梯形 D.平行四边形
4.如图,?ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
5.如图,在四边形ABCD中,点E是BC边的中点,连结DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )21·cn·jy·com
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
6.以任意不在同一直线上的A,B,C三点为其中的三个顶点,作不同的平行四边形,最多可以作__________个.?www.21-cn-jy.com
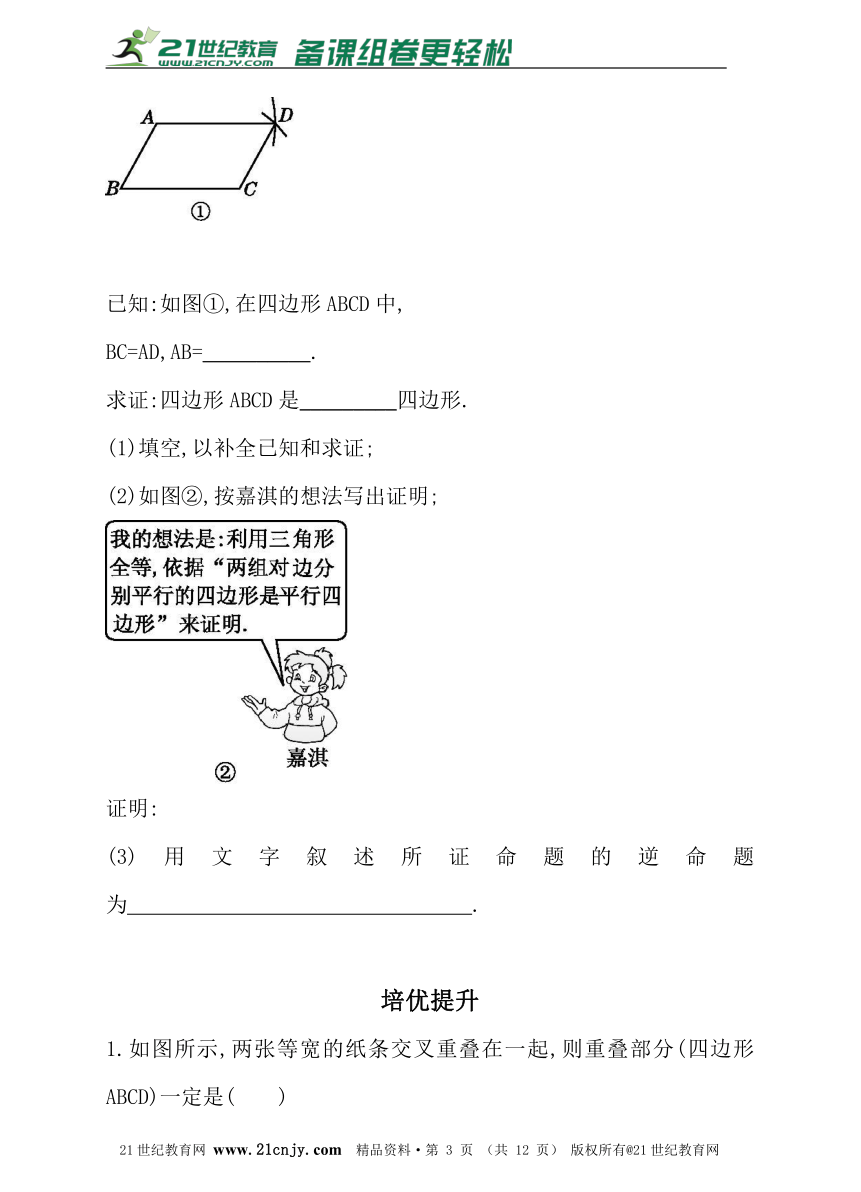
7.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图①的四边形ABCD,并写出了如下不完整的已知和求证.2·1·c·n·j·y
已知:如图①,在四边形ABCD中,
BC=AD,AB=__________.?
求证:四边形ABCD是_________四边形.?
(1)填空,以补全已知和求证;
(2)如图②,按嘉淇的想法写出证明;
证明:
(3)用文字叙述所证命题的逆命题为 .?
培优提升
1.如图所示,两张等宽的纸条交叉重叠在一起,则重叠部分(四边形ABCD)一定是( )
A.正方形
B.平行四边形
C.三角形
D.长方形
2.用两个可以互相重合的不等边三角形来拼平行四边形,共可拼( )
A.1个 B.3个
C.6个 D.无数个
3.如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要添加一个条件是( )【来源:21·世纪·教育·网】
A.AB=DC B.∠1=∠2
C.AB=AD D.∠D=∠B
4.如图,E、F分别是?ABCD两对边的中点,则图中平行四边形有( )
A.3个 B.4个
C.5个 D.6个
5.如图,在平面直角坐标系中,以O(0,0)、A(1,1)、B(3,0)为顶点构造平行四边形,下列不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1)
C.(-2,1) D.(2,-1)
6.如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是.(只填写一个条件,不使用图形以外的字母和线段)21·世纪*教育网
7.已知一个凸四边形ABCD的四条边的长顺次是a、b、c、d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,那么四边形ABCD是__________.?
8.已知:如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.www-2-1-cnjy-com
求证:四边形ABCD为平行四边形.
9.如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连结BE. 2-1-c-n-j-y
(1)求证:四边形BCED'是平行四边形.
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
10.如图,在?ABCD中,BD为对角线,EF垂直平分BD,分别交AD、BC于点E、F,交BD于点O. 21*cnjy*com
(1)试说明:BF=DE;
(2)试说明:△ABE≌△CDF;
(3)如果在?ABCD中,AB=5,AD=10,有两动点P、Q分别从B、D两点同时出发,沿△BAE和△DFC各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
参考答案
【基础训练】
1.【答案】C
解:根据平行四边形的判定定理1、2及定义可知①与②,③与④,①与③,②与④都能判定四边形ABCD是平行四边形,故选C.
2.【答案】C
3.【答案】D
解:∵(a-c)2+(b-d)2=0,∴a=c,b=d.∴这个四边形是平行四边形.故选D.
4.【答案】D 5.【答案】D
6.【答案】3
解:如图,以任意不在同一直线上的三点A,B,C为其中的三个顶点可作3个不同的平行四边形:?ABCD,?ABFC,?AEBC.【来源:21cnj*y.co*m】
7.(1)CD;平行
(2)证明:连结BD,如图.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形.
(3)平行四边形的对边相等
【培优提升】
1.【答案】B
解:两组对边分别平行的四边形是平行四边形.
2.【答案】B
3.【答案】D
解:符合条件AD∥BC,AB=DC,可能是等腰梯形,故选项A错误;根据∠1=∠2,推出AD∥BC,不能推出四边形ABCD为平行四边形,故选项B错误;根据AB=AD和AD∥BC不能推出四边形ABCD为平行四边形,故选项C错误;∵AD∥BC,∴∠1=∠2,又∵∠B=∠D,∴∠BAC=∠DCA,∴AB∥CD,∴四边形ABCD是平行四边形,故选项D正确.故选D.
4.【答案】D 5.【答案】A
6.【答案】AB=CD(答案不唯一)
7.【答案】平行四边形
解:由a2+ab-ac-bc=0,可知(a+b)(a-c)=0,则a-c=0,即a=c;由b2+bc-bd-cd=0,可知(b+c)(b-d)=0,则b-d=0,即b=d(其中a,b,c,d都是正数,a+b、b+c一定不等于0).由a=c,b=d知四边形ABCD的两组对边分别相等,则四边形ABCD是平行四边形.21cnjy.com
8.证明:∵AB∥CD,∴∠BAE=∠DCF.
∵BE∥DF,∴∠BEF=∠DFE.
∴∠AEB=∠CFD.
在△AEB和△CFD中,
∴△AEB≌△CFD.∴AB=CD.
∵AB∥CD,
∴四边形ABCD是平行四边形.
9.证明:(1)如图,∵△DAE沿着直线l折叠得到△D'AE,
∴DE=D'E,∠1=∠2.
又∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠1=∠3,∴∠2=∠3,
∴D'A=D'E,∴D'A=DE,
∴AB-AD'=DC-DE,
即CE=D'B,
∴四边形BCED'是平行四边形.
(2)∵BE平分∠ABC,∴∠4=∠ABC.
又∵∠3=∠BAD,
∴∠3+∠4=(∠ABC+∠BAD).
又∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠3+∠4=90°,∴∠AEB=90°,
∴AB2=AE2+BE2.
10.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ODE=∠OBF.
∵EF垂直平分BD,∴OB=OD.
在△OBF和△ODE中,
∴△FOB≌△ODE,∴BF=DE.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,AD=BC,
又∵BF=DE,∴AE=CF.
在△ABE和△CDF中,
,∴△ABE≌△CDF.
(3)∵EF垂直平分BD,∴BF=DF.
∴△DFC的周长是DF+CF+CD=BF+CF+CD=BC+CD=15.
①当点P在AB上,点Q在CD上时,如图①,
∵四边形BPDQ是平行四边形,∴BP=DQ,
∴m+n=BP+DF+CF+CQ=DF+CF+CQ+DQ=DF+CF+CD=15;
②当点P在AE上,点Q在CF上时,如图②,
∵四边形BPDQ为平行四边形.∴DP=BQ.
又∵AD=BC.∴AP=CQ,
∴m+n
=AB+AP+DF+FQ
=CD+CQ+DF+FQ
=DF+CF+CD
=15;
③当点P在BE上,点Q在DF上时,如图③.∵四边形BPDQ为平行四边形.∴BP=DQ.由(2)知△ABE≌△CDF,∴BE=DF,∴PE=QF.又∵AE=CF.
∴m+n
=AB+AE+PE+DQ
=CD+CF+FQ+DQ
=DF+CF+CD
=15.
分析:本题的精彩之处在于将动点与平行四边形相结合进行考查,注意(3)题应考虑全面.
核心笔记: 如图,已知四边形ABCD,
判定方法
主要内容
数学语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,∴四边形ABCD是平行四边形
基础训练
1.点A,B,C,D在同一平面内且任意三点不共线,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD中任选两个作为条件,能使四边形ABCD为平行四边形的选法有( )21世纪教育网版权所有
A.6种 B.5种 C.4种 D.3种
2.在四边形ABCD中,∠A∶∠B∶∠C∶∠D的比如下,其中能判断四边形是平行四边形的是( )
A.1∶2∶3∶4 B.2∶3∶4∶5
C.3∶2∶3∶2 D.3∶3∶5∶4
3.一个四边形的四条边长依次为a,b,c,d,且满足(a-c)2+(b-d)2=0,则这个四边形一定是( )21教育网
A.正方形 B.长方形
C.梯形 D.平行四边形
4.如图,?ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
5.如图,在四边形ABCD中,点E是BC边的中点,连结DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )21·cn·jy·com
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE
6.以任意不在同一直线上的A,B,C三点为其中的三个顶点,作不同的平行四边形,最多可以作__________个.?www.21-cn-jy.com
7.嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图①的四边形ABCD,并写出了如下不完整的已知和求证.2·1·c·n·j·y
已知:如图①,在四边形ABCD中,
BC=AD,AB=__________.?
求证:四边形ABCD是_________四边形.?
(1)填空,以补全已知和求证;
(2)如图②,按嘉淇的想法写出证明;
证明:
(3)用文字叙述所证命题的逆命题为 .?
培优提升
1.如图所示,两张等宽的纸条交叉重叠在一起,则重叠部分(四边形ABCD)一定是( )
A.正方形
B.平行四边形
C.三角形
D.长方形
2.用两个可以互相重合的不等边三角形来拼平行四边形,共可拼( )
A.1个 B.3个
C.6个 D.无数个
3.如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要添加一个条件是( )【来源:21·世纪·教育·网】
A.AB=DC B.∠1=∠2
C.AB=AD D.∠D=∠B
4.如图,E、F分别是?ABCD两对边的中点,则图中平行四边形有( )
A.3个 B.4个
C.5个 D.6个
5.如图,在平面直角坐标系中,以O(0,0)、A(1,1)、B(3,0)为顶点构造平行四边形,下列不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1)
C.(-2,1) D.(2,-1)
6.如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是.(只填写一个条件,不使用图形以外的字母和线段)21·世纪*教育网
7.已知一个凸四边形ABCD的四条边的长顺次是a、b、c、d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,那么四边形ABCD是__________.?
8.已知:如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE.www-2-1-cnjy-com
求证:四边形ABCD为平行四边形.
9.如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕l交CD边于点E,连结BE. 2-1-c-n-j-y
(1)求证:四边形BCED'是平行四边形.
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
10.如图,在?ABCD中,BD为对角线,EF垂直平分BD,分别交AD、BC于点E、F,交BD于点O. 21*cnjy*com
(1)试说明:BF=DE;
(2)试说明:△ABE≌△CDF;
(3)如果在?ABCD中,AB=5,AD=10,有两动点P、Q分别从B、D两点同时出发,沿△BAE和△DFC各边运动一周,即点P自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
参考答案
【基础训练】
1.【答案】C
解:根据平行四边形的判定定理1、2及定义可知①与②,③与④,①与③,②与④都能判定四边形ABCD是平行四边形,故选C.
2.【答案】C
3.【答案】D
解:∵(a-c)2+(b-d)2=0,∴a=c,b=d.∴这个四边形是平行四边形.故选D.
4.【答案】D 5.【答案】D
6.【答案】3
解:如图,以任意不在同一直线上的三点A,B,C为其中的三个顶点可作3个不同的平行四边形:?ABCD,?ABFC,?AEBC.【来源:21cnj*y.co*m】
7.(1)CD;平行
(2)证明:连结BD,如图.
在△ABD和△CDB中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥CD,AD∥CB.
∴四边形ABCD是平行四边形.
(3)平行四边形的对边相等
【培优提升】
1.【答案】B
解:两组对边分别平行的四边形是平行四边形.
2.【答案】B
3.【答案】D
解:符合条件AD∥BC,AB=DC,可能是等腰梯形,故选项A错误;根据∠1=∠2,推出AD∥BC,不能推出四边形ABCD为平行四边形,故选项B错误;根据AB=AD和AD∥BC不能推出四边形ABCD为平行四边形,故选项C错误;∵AD∥BC,∴∠1=∠2,又∵∠B=∠D,∴∠BAC=∠DCA,∴AB∥CD,∴四边形ABCD是平行四边形,故选项D正确.故选D.
4.【答案】D 5.【答案】A
6.【答案】AB=CD(答案不唯一)
7.【答案】平行四边形
解:由a2+ab-ac-bc=0,可知(a+b)(a-c)=0,则a-c=0,即a=c;由b2+bc-bd-cd=0,可知(b+c)(b-d)=0,则b-d=0,即b=d(其中a,b,c,d都是正数,a+b、b+c一定不等于0).由a=c,b=d知四边形ABCD的两组对边分别相等,则四边形ABCD是平行四边形.21cnjy.com
8.证明:∵AB∥CD,∴∠BAE=∠DCF.
∵BE∥DF,∴∠BEF=∠DFE.
∴∠AEB=∠CFD.
在△AEB和△CFD中,
∴△AEB≌△CFD.∴AB=CD.
∵AB∥CD,
∴四边形ABCD是平行四边形.
9.证明:(1)如图,∵△DAE沿着直线l折叠得到△D'AE,
∴DE=D'E,∠1=∠2.
又∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠1=∠3,∴∠2=∠3,
∴D'A=D'E,∴D'A=DE,
∴AB-AD'=DC-DE,
即CE=D'B,
∴四边形BCED'是平行四边形.
(2)∵BE平分∠ABC,∴∠4=∠ABC.
又∵∠3=∠BAD,
∴∠3+∠4=(∠ABC+∠BAD).
又∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠3+∠4=90°,∴∠AEB=90°,
∴AB2=AE2+BE2.
10.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠ODE=∠OBF.
∵EF垂直平分BD,∴OB=OD.
在△OBF和△ODE中,
∴△FOB≌△ODE,∴BF=DE.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,AD=BC,
又∵BF=DE,∴AE=CF.
在△ABE和△CDF中,
,∴△ABE≌△CDF.
(3)∵EF垂直平分BD,∴BF=DF.
∴△DFC的周长是DF+CF+CD=BF+CF+CD=BC+CD=15.
①当点P在AB上,点Q在CD上时,如图①,
∵四边形BPDQ是平行四边形,∴BP=DQ,
∴m+n=BP+DF+CF+CQ=DF+CF+CQ+DQ=DF+CF+CD=15;
②当点P在AE上,点Q在CF上时,如图②,
∵四边形BPDQ为平行四边形.∴DP=BQ.
又∵AD=BC.∴AP=CQ,
∴m+n
=AB+AP+DF+FQ
=CD+CQ+DF+FQ
=DF+CF+CD
=15;
③当点P在BE上,点Q在DF上时,如图③.∵四边形BPDQ为平行四边形.∴BP=DQ.由(2)知△ABE≌△CDF,∴BE=DF,∴PE=QF.又∵AE=CF.
∴m+n
=AB+AE+PE+DQ
=CD+CF+FQ+DQ
=DF+CF+CD
=15.
分析:本题的精彩之处在于将动点与平行四边形相结合进行考查,注意(3)题应考虑全面.
