18.2.2 由对角线的关系判定平行四边形 同步练习
文档属性
| 名称 | 18.2.2 由对角线的关系判定平行四边形 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 475.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 00:00:00 | ||
图片预览


文档简介
18.2.2 由对角线的关系判定平行四边形
核心笔记: 由对角线关系判定平行四边形:如图,在四边形ABCD中,AC,BD相交于点O.若OA=OC,OB=OD,则四边形ABCD为平行四边形.
即:对角线互相平分的四边形是平行四边形.
基础训练
1.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )21教育网
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
2.下列命题中,真命题有( )
①对角线互相平分的四边形是平行四边形
②两组对角分别相等的四边形是平行四边形
③一组对边平行,另一组对边相等的四边形是平行四边形
A.3个 B.2个 C.1个 D.0个
3.在给定的条件中,能作出平行四边形的是( )
A.以60 cm为一条对角线长,20 cm、34 cm为两条邻边长
B.以20 cm、36 cm为对角线长,22 cm为一条边长
C.以6 cm为一条对角线长,3 cm、10 cm为两条邻边长
D.以6 cm、10 cm为对角线长,8 cm为一条边长
4.在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.(1)(2) B.(1)(3)(4)
C.(2)(3) D.(2)(3)(4)
5.如图所示,AO=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.?
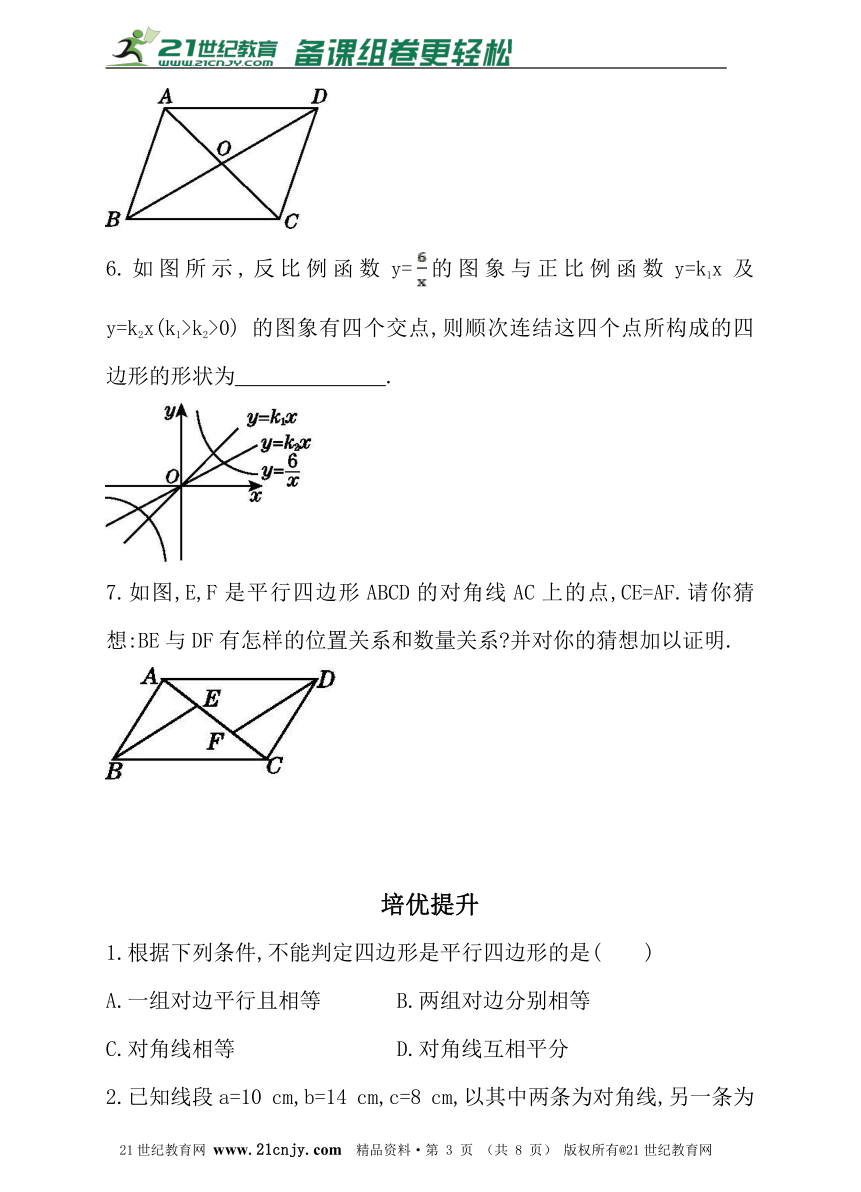
6.如图所示,反比例函数y=的图象与正比例函数y=k1x及y=k2x(k1>k2>0) 的图象有四个交点,则顺次连结这四个点所构成的四边形的形状为 .21·cn·jy·com
7.如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
培优提升
1.根据下列条件,不能判定四边形是平行四边形的是( )
A.一组对边平行且相等 B.两组对边分别相等
C.对角线相等 D.对角线互相平分
2.已知线段a=10 cm,b=14 cm,c=8 cm,以其中两条为对角线,另一条为边画平行四边形,可以画出不同形状的平行四边形共( )
A.0个 B.1个 C.2个 D.3个
3.已知:如图,在?ABCD中,对角线AC,BD相交于O,E,F是对角线AC上的两点,给出下列四个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
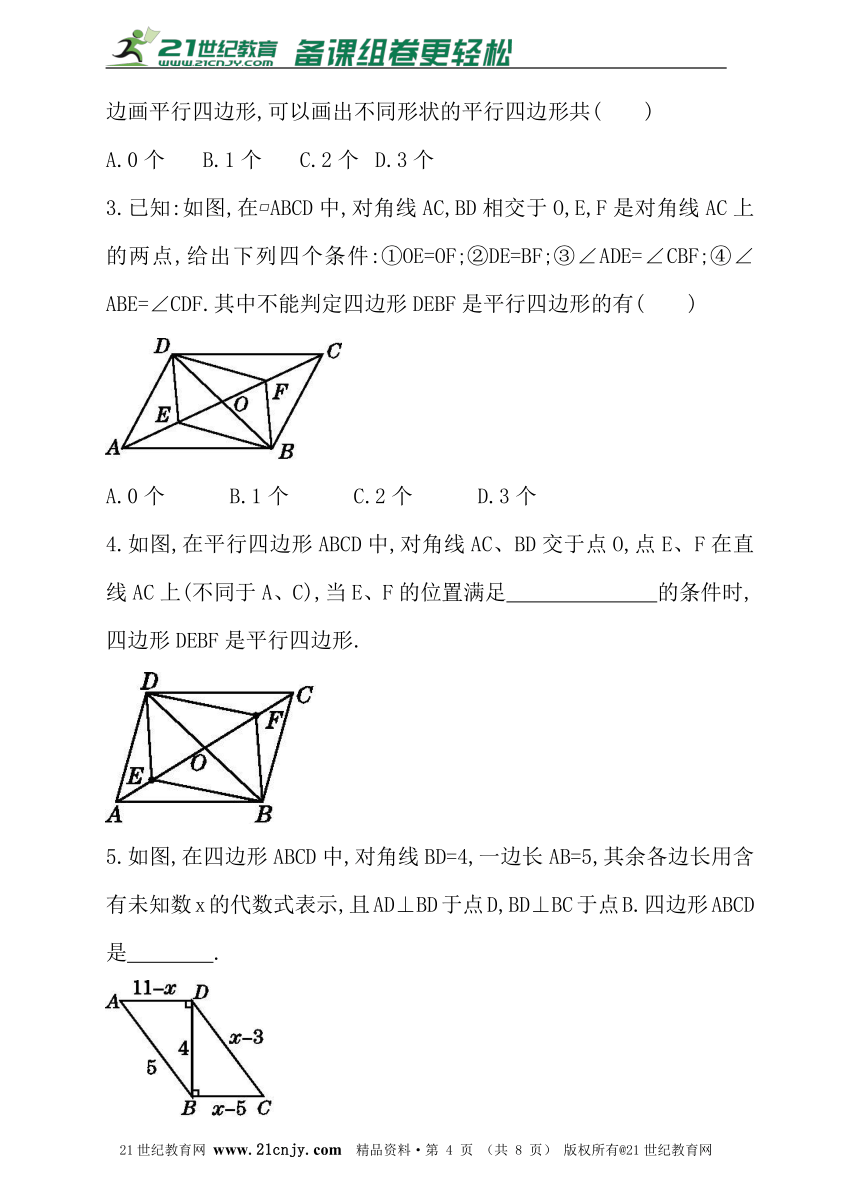
4.如图,在平行四边形ABCD中,对角线AC、BD交于点O,点E、F在直线AC上(不同于A、C),当E、F的位置满足 的条件时,四边形DEBF是平行四边形.【来源:21·世纪·教育·网】
5.如图,在四边形ABCD中,对角线BD=4,一边长AB=5,其余各边长用含有未知数x的代数式表示,且AD⊥BD于点D,BD⊥BC于点B.四边形ABCD是 .www-2-1-cnjy-com
6.如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,要证明四边形AECF是平行四边形,最简单的方法是根据 来证
明.
7.如图,点D、E分别是△ABC的边AB、AC的中点,点F
在DE的延长线上且EF=ED,则四边形ADCF是 ,理由
是 .四边形BCFD是 ,理由
是 .
8.如图,?ABCD中,点E、F在对角线BD上,且BE=DF,求证:
(1)AE=CF.
(2)四边形AECF是平行四边形.
9.如图①,?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连结EG,FG,FH,EH.www.21-cn-jy.com
(1)求证:四边形EGFH是平行四边形;
(2)如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】C
5.【答案】8
解:根据对角线互相平分的四边形为平行四边形来求解.
6.【答案】平行四边形
解:反比例函数y=的图象与正比例函数y=k1x的图象有两个交点,交点关于原点对称,同理反比例函数y=的图象与正比例函数y=k2x的图象也有两个交点,交点也关于原点对称,顺次连结四个点所构成的四边形是对角线互相平分的四边形,故是平行四边形.21cnjy.com
7.解:猜想:BE∥DF,BE=DF.
证明:如图,连结BD交AC于点O,连结DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO.
∵AF=CE,∴AE=CF.易得EO=FO.
∴四边形BEDF是平行四边形.
∴BE∥DF.
【培优提升】
1.【答案】C 2.【答案】C 3.【答案】B
4.【答案】OE=OF
解:根据四边形ABCD是平行四边形,可得DO=BO,再由条件OE=OF,根据对角线互相平分的四边形是平行四边形可判定四边形DEBF是平行四边形.答案不唯一.21·世纪*教育网
5.【答案】平行四边形
解:在Rt△BCD中,根据勾股定理,得BC2+BD2=DC2,
即(x-5)2+42=(x-3)2,解得x=8.
所以AD=11-8=3,BC=8-5=3,DC=8-3=5,
所以AD=BC,AB=DC.
所以四边形ABCD是平行四边形.
6.【答案】对角线互相平分的四边形是平行四边形
7.【答案】平行四边形;对角线互相平分的四边形是平行四边形;
平行四边形;一组对边平行且相等的四边形是平行四边形
8.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF,∴AE=CF.
(2)连结AC,交BD于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形.21世纪教育网版权所有
9.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,∴∠EAO=∠FCO.
∵OA=OC,∠AOE=∠COF,
∴△OAE≌△OCF,∴OE=OF.
同理OG=OH,∴四边形EGFH是平行四边形.
(2)解:?GBCH,?ABFE,?EFCD,?EGFH.
核心笔记: 由对角线关系判定平行四边形:如图,在四边形ABCD中,AC,BD相交于点O.若OA=OC,OB=OD,则四边形ABCD为平行四边形.
即:对角线互相平分的四边形是平行四边形.
基础训练
1.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )21教育网
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
2.下列命题中,真命题有( )
①对角线互相平分的四边形是平行四边形
②两组对角分别相等的四边形是平行四边形
③一组对边平行,另一组对边相等的四边形是平行四边形
A.3个 B.2个 C.1个 D.0个
3.在给定的条件中,能作出平行四边形的是( )
A.以60 cm为一条对角线长,20 cm、34 cm为两条邻边长
B.以20 cm、36 cm为对角线长,22 cm为一条边长
C.以6 cm为一条对角线长,3 cm、10 cm为两条邻边长
D.以6 cm、10 cm为对角线长,8 cm为一条边长
4.在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.(1)(2) B.(1)(3)(4)
C.(2)(3) D.(2)(3)(4)
5.如图所示,AO=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.?
6.如图所示,反比例函数y=的图象与正比例函数y=k1x及y=k2x(k1>k2>0) 的图象有四个交点,则顺次连结这四个点所构成的四边形的形状为 .21·cn·jy·com
7.如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
培优提升
1.根据下列条件,不能判定四边形是平行四边形的是( )
A.一组对边平行且相等 B.两组对边分别相等
C.对角线相等 D.对角线互相平分
2.已知线段a=10 cm,b=14 cm,c=8 cm,以其中两条为对角线,另一条为边画平行四边形,可以画出不同形状的平行四边形共( )
A.0个 B.1个 C.2个 D.3个
3.已知:如图,在?ABCD中,对角线AC,BD相交于O,E,F是对角线AC上的两点,给出下列四个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
4.如图,在平行四边形ABCD中,对角线AC、BD交于点O,点E、F在直线AC上(不同于A、C),当E、F的位置满足 的条件时,四边形DEBF是平行四边形.【来源:21·世纪·教育·网】
5.如图,在四边形ABCD中,对角线BD=4,一边长AB=5,其余各边长用含有未知数x的代数式表示,且AD⊥BD于点D,BD⊥BC于点B.四边形ABCD是 .www-2-1-cnjy-com
6.如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,要证明四边形AECF是平行四边形,最简单的方法是根据 来证
明.
7.如图,点D、E分别是△ABC的边AB、AC的中点,点F
在DE的延长线上且EF=ED,则四边形ADCF是 ,理由
是 .四边形BCFD是 ,理由
是 .
8.如图,?ABCD中,点E、F在对角线BD上,且BE=DF,求证:
(1)AE=CF.
(2)四边形AECF是平行四边形.
9.如图①,?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连结EG,FG,FH,EH.www.21-cn-jy.com
(1)求证:四边形EGFH是平行四边形;
(2)如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】C
5.【答案】8
解:根据对角线互相平分的四边形为平行四边形来求解.
6.【答案】平行四边形
解:反比例函数y=的图象与正比例函数y=k1x的图象有两个交点,交点关于原点对称,同理反比例函数y=的图象与正比例函数y=k2x的图象也有两个交点,交点也关于原点对称,顺次连结四个点所构成的四边形是对角线互相平分的四边形,故是平行四边形.21cnjy.com
7.解:猜想:BE∥DF,BE=DF.
证明:如图,连结BD交AC于点O,连结DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO.
∵AF=CE,∴AE=CF.易得EO=FO.
∴四边形BEDF是平行四边形.
∴BE∥DF.
【培优提升】
1.【答案】C 2.【答案】C 3.【答案】B
4.【答案】OE=OF
解:根据四边形ABCD是平行四边形,可得DO=BO,再由条件OE=OF,根据对角线互相平分的四边形是平行四边形可判定四边形DEBF是平行四边形.答案不唯一.21·世纪*教育网
5.【答案】平行四边形
解:在Rt△BCD中,根据勾股定理,得BC2+BD2=DC2,
即(x-5)2+42=(x-3)2,解得x=8.
所以AD=11-8=3,BC=8-5=3,DC=8-3=5,
所以AD=BC,AB=DC.
所以四边形ABCD是平行四边形.
6.【答案】对角线互相平分的四边形是平行四边形
7.【答案】平行四边形;对角线互相平分的四边形是平行四边形;
平行四边形;一组对边平行且相等的四边形是平行四边形
8.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF,∴AE=CF.
(2)连结AC,交BD于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又∵BE=DF,∴OE=OF,∴四边形AECF是平行四边形.21世纪教育网版权所有
9.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,∴∠EAO=∠FCO.
∵OA=OC,∠AOE=∠COF,
∴△OAE≌△OCF,∴OE=OF.
同理OG=OH,∴四边形EGFH是平行四边形.
(2)解:?GBCH,?ABFE,?EFCD,?EGFH.
