18.2.3 平行四边形的判定和性质的综合运用 同步练习
文档属性
| 名称 | 18.2.3 平行四边形的判定和性质的综合运用 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 566.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 22:24:19 | ||
图片预览



文档简介
18.2.3 平行四边形的判定和性质的综合运用
核心笔记:
1.平行四边形的性质:
(1)平行四边形的对边平行且相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
2.平行四边形的判定:
(1)两组对边分别平行的四边形;
(2)两组对边分别相等的四边形;
(3)一组对边平行且相等的四边形;
(4)两组对角分别相等的四边形;
(5)对角线互相平分的四边形.
基础训练
1.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,另一组对边相等;③一组对边平行且相等;④一组对边平行,一条对角线被另一条对角线平分,不能判定其为平行四边形的是( )21·cn·jy·com
A.① B.② C.③ D.④
2.平行四边形一组对角的平分线( )
A.在同一条直线上
B.互相平行
C.既不互相平行,也不在同一条直线上
D.在同一条直线上,或互相平行
3.根据下列条件,能作出平行四边形的是( )
A.两条邻边长分别是3 cm和7 cm,其夹角为40°
B.相邻两边的长分别是2 cm和4 cm,一条对角线长是7 cm
C.一条对角线长为6 cm,另一条对角线长为10 cm,一条边长为8 cm
D.一条边长为7 cm,两条对角线长分别为6 cm和8 cm
4.小玲的爸爸在制作平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是___________.?21·世纪*教育网
5.已知线段BC及BC外一点A,以A点为顶点,BC为对角线可以作___________个平行四边形,若以点A为顶点,BC为一边,可作___________个平行四边形.?21*cnjy*com
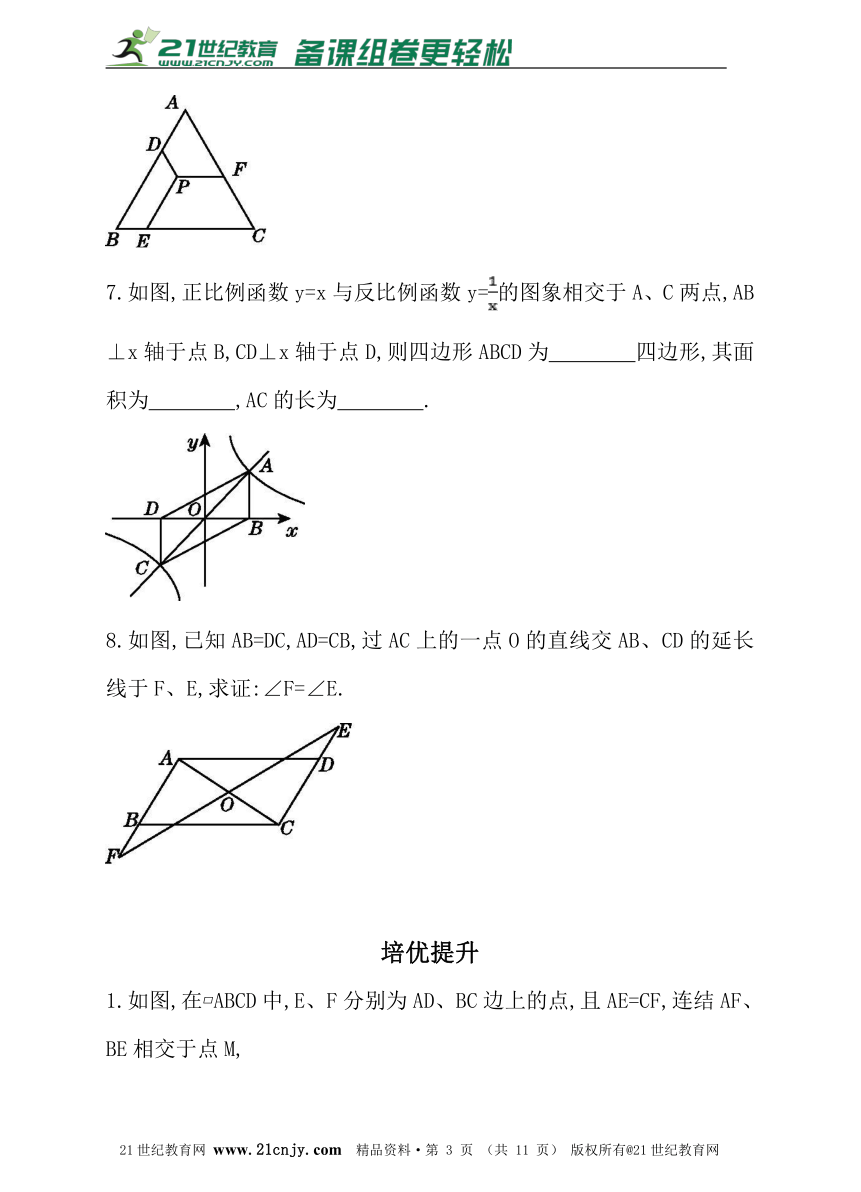
6.如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AB,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=___________.
7.如图,正比例函数y=x与反比例函数y=的图象相交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD为 四边形,其面积为 ,AC的长为 .【来源:21cnj*y.co*m】
?
8.如图,已知AB=DC,AD=CB,过AC上的一点O的直线交AB、CD的延长线于F、E,求证:∠F=∠E.21教育网
培优提升
1.如图,在?ABCD中,E、F分别为AD、BC边上的点,且AE=CF,连结AF、BE相交于点M,
连结CE、DF相交于点N,则图中除四边形ABCD之外的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
2.在平行四边形ABCD中,按下列条件得到的四边形EFGH不一定是平行四边形的是( )
A B C D
3.如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:【出处:21教育名师】
甲:连结BD、CE,两线段相交于P点,则P即为所求;
乙:先取CD的中点M,连结AM,再以A为圆心,AB长为半径画弧,交AM于P点,则P即为所求.对于甲、乙两人的作法,下列判断正确的是( )【版权所有:21教育】
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
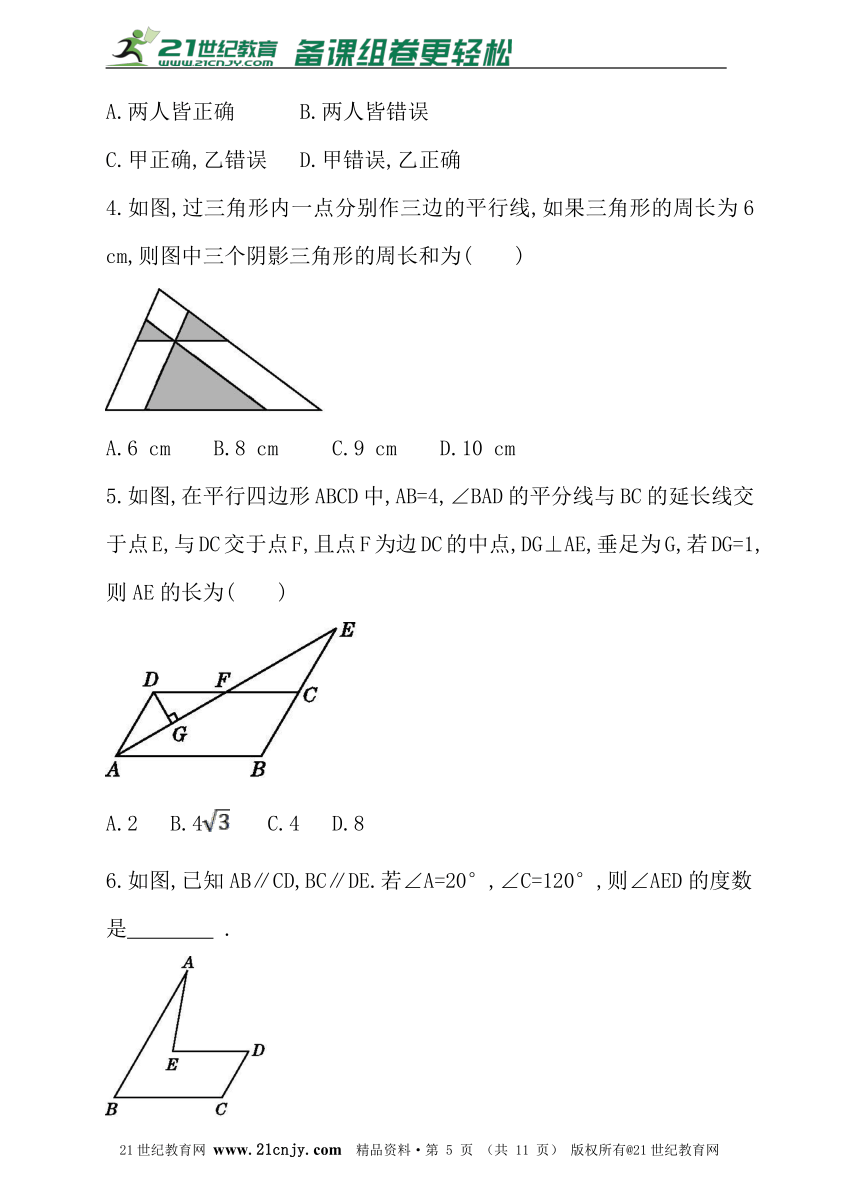
4.如图,过三角形内一点分别作三边的平行线,如果三角形的周长为6 cm,则图中三个阴影三角形的周长和为( )www-2-1-cnjy-com
A.6 cm B.8 cm C.9 cm D.10 cm
5.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )21*cnjy*com
A.2 B.4 C.4 D.8
6.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数
是 .
7.如图,在△ABC中,AB=6,AC=4,AD是BC边上的中线,则AD的取值范围是 .
8.如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点B的坐标为(3,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D在第一象限,那么点D的坐标是 .
9.如图,将?ABCD的AD边延长至点E,使DE=AD,连结CE,F是BC边的中点,连结FD.
求证:四边形CEDF是平行四边形.
10.张大伯承包了一个呈四边形的池塘,如图所示,它的四个顶点A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图. 2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】B
解:①由“一组对边平行,一组对角相等”,再根据平行线的性质,可得另一组对角也相等,故一组对边平行,一组对角相等的四边形是平行四边形,故①不符合题意;②由“一组对边平行,另一组对边相等”不能判定该四边形为平行四边形,故②符合题意;③由“一组对边平行且相等”可以判定该四边形为平行四边形,故③不符合题意;④一组对边平行,一条对角线被另一条对角线平分,可利用全等得出这组对边也相等,可判定该四边形为平行四边形,故④不符合题意,故选B.
2.【答案】D 3.【答案】A
4.【答案】对角线互相平分的四边形是平行四边形
5.【答案】1;2
6.【答案】8
解:过E点作EG∥PD交AB于G,过D点作DH∥PF交AC于H,∵PD∥AC,PE∥AB,∴PD∥HF,PE∥DG,∴四边形DGEP和四边形DPFH都为平行四边形,∴EG=DP,PE=GD,PF=DH.又∵△ABC是等边三角形,EG∥AC,∴△BEG为等边三角形,∴EG=PD=GB,同理可证
DH=PF=AD,∴PD+PE+PF=BG+GD+AD=AB=8.
7.【答案】平行;2;2
8.【答案】证明:∵AB=DC,AD=CB,
∴四边形ABCD是平行四边形.
∴AB∥CD,
∴∠F=∠E.
【培优提升】
1.【答案】C
解:∵四边形ABCD为平行四边形,∴AD∥
BC,AD=BC.∵AE=CF,∴DE=BF,∴四边形AECF和四边形DEBF都是平行四边形,∴AF∥CE,BE∥DF,∴四边形EMFN也是平行四边形.故除四边形ABCD之外的平行四边形有3个,选C.21cnjy.com
2.【答案】A
解:A中由于所给已知条件只有角的关系,三角形边之间没有等量关系,不能证明三角形全等或边之间平行,也就无法证明四边形EFGH是平行四边形.21教育名师原创作品
3.【答案】C
解:甲正确,乙错误,理由是:在甲的作法中,∵正五边形的每个内角的度数是=108°,AB=BC=CD=DE=AE,∴∠DEC=∠
DCE=×(180°-108°)=36°,同理∠CBD=∠CDB=36°,∴∠ABP=∠
AEP=108°-36°=72°,∴∠BPE=360°-108°-72°-72°=108°=∠
A,∴四边形ABPE是平行四边形,即甲正确;在乙的作法中,∵∠
BAE=108°,∴∠BAM=∠EAM=54°,∵AB=AE=AP,∴∠ABP=∠
APB=×(180°-54°)=63°,∠AEP=∠APE=63°,∴∠
BPE=360°-108°-63°-63°≠108°,即∠ABP=∠AEP,∠BAE≠∠
BPE,∴四边形ABPE不是平行四边形,即乙错误.故选C.
4.【答案】A
5.【答案】B
解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE.∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD.∵DG⊥AF,∴AG=GF=AF.又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2.在Rt△ADG中,根据勾股定理得AG=,则AF=2AG=2.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF.在△ADF和△ECF中,21世纪教育网版权所有
,
∴△ADF≌△ECF,∴AF=EF,则AE=2AF=4.故选B.
6.【答案】80°
解:如图,延长DE交AB于F.
∵AB∥CD,BC∥DE,∴四边形BCDF为平行四边形,∴∠BFD=∠C=120°,
∴∠AFE=60°,∴∠AED=∠A+∠AFE=80°.
7.【答案】1解:延长AD到E使DE=AD,连结BE,CE.又因为BD=CD,所以四边形ABEC为平行四边形,所以BE=AC=4,所以28.【答案】(2,5)或(8,5)
解:由平行四边形的性质和题干要求,可知D点的纵坐标一定是5;
又由A点相对于B点向左移动了3个单位长度,故可得点D的横坐标为5-3=2,即顶点D的坐标为(2,5);再由B点相对于A点向右移动了3个单位长度,故可得点D的横坐标为5+3=8,即顶点D的坐标为(8,5).故答案为(2,5)或(8,5).www.21-cn-jy.com
9.证明:∵四边形ABCD是平行四边形,∴AD??BC.
∵F是BC中点,∴FC=BC.
又∵DE=AD,∴FC=DE,
又∵DE∥FC,
∴四边形CEDF是平行四边形.
10.解:能实现.方法一:如图①所示.
连结对角线AC,BD交于点O,
过点A,C分别作BD的平行线,过点B,D分别作AC的平行线,
四条平行线依次交于M,N,G,H四点,
则可得四边形MNGH、四边形AODH、四边形AOBM、四边形BOCN、四边形OCGD均为平行四边形.2-1-c-n-j-y
在?AODH中,AO=HD,AH=OD,AD=AD,
∴△AHD≌△DOA,
∴S△AHD=S△AOD,同理S△COD=S△CGD,S△BOC=S△BNC,S△AOB=S△AMB,
∴S?MNGH=2S四边形ABCD.故?MNGH即为所求.
方法二:如图②.连结AC,分别过点B、D作EF∥AC,DH∥AC;延长DC交EF于点F.过点A作EH∥DF交EF于点E,交DH于点H,易知四边形AEFC、四边形ACDH、四边形EFDH均为平行四边形,且S?ACFE=2S△ABC,S?ACDH=2S△ACD,故S?EFDH=2S四边形ABCD.即?EFDH为扩建后的图形.【来源:21·世纪·教育·网】
核心笔记:
1.平行四边形的性质:
(1)平行四边形的对边平行且相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
2.平行四边形的判定:
(1)两组对边分别平行的四边形;
(2)两组对边分别相等的四边形;
(3)一组对边平行且相等的四边形;
(4)两组对角分别相等的四边形;
(5)对角线互相平分的四边形.
基础训练
1.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,另一组对边相等;③一组对边平行且相等;④一组对边平行,一条对角线被另一条对角线平分,不能判定其为平行四边形的是( )21·cn·jy·com
A.① B.② C.③ D.④
2.平行四边形一组对角的平分线( )
A.在同一条直线上
B.互相平行
C.既不互相平行,也不在同一条直线上
D.在同一条直线上,或互相平行
3.根据下列条件,能作出平行四边形的是( )
A.两条邻边长分别是3 cm和7 cm,其夹角为40°
B.相邻两边的长分别是2 cm和4 cm,一条对角线长是7 cm
C.一条对角线长为6 cm,另一条对角线长为10 cm,一条边长为8 cm
D.一条边长为7 cm,两条对角线长分别为6 cm和8 cm
4.小玲的爸爸在制作平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是___________.?21·世纪*教育网
5.已知线段BC及BC外一点A,以A点为顶点,BC为对角线可以作___________个平行四边形,若以点A为顶点,BC为一边,可作___________个平行四边形.?21*cnjy*com
6.如图,已知等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AB,PF∥BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF=___________.
7.如图,正比例函数y=x与反比例函数y=的图象相交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD为 四边形,其面积为 ,AC的长为 .【来源:21cnj*y.co*m】
?
8.如图,已知AB=DC,AD=CB,过AC上的一点O的直线交AB、CD的延长线于F、E,求证:∠F=∠E.21教育网
培优提升
1.如图,在?ABCD中,E、F分别为AD、BC边上的点,且AE=CF,连结AF、BE相交于点M,
连结CE、DF相交于点N,则图中除四边形ABCD之外的平行四边形有( )
A.1个 B.2个 C.3个 D.4个
2.在平行四边形ABCD中,按下列条件得到的四边形EFGH不一定是平行四边形的是( )
A B C D
3.如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:【出处:21教育名师】
甲:连结BD、CE,两线段相交于P点,则P即为所求;
乙:先取CD的中点M,连结AM,再以A为圆心,AB长为半径画弧,交AM于P点,则P即为所求.对于甲、乙两人的作法,下列判断正确的是( )【版权所有:21教育】
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
4.如图,过三角形内一点分别作三边的平行线,如果三角形的周长为6 cm,则图中三个阴影三角形的周长和为( )www-2-1-cnjy-com
A.6 cm B.8 cm C.9 cm D.10 cm
5.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )21*cnjy*com
A.2 B.4 C.4 D.8
6.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数
是 .
7.如图,在△ABC中,AB=6,AC=4,AD是BC边上的中线,则AD的取值范围是 .
8.如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点B的坐标为(3,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D在第一象限,那么点D的坐标是 .
9.如图,将?ABCD的AD边延长至点E,使DE=AD,连结CE,F是BC边的中点,连结FD.
求证:四边形CEDF是平行四边形.
10.张大伯承包了一个呈四边形的池塘,如图所示,它的四个顶点A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图. 2·1·c·n·j·y
参考答案
【基础训练】
1.【答案】B
解:①由“一组对边平行,一组对角相等”,再根据平行线的性质,可得另一组对角也相等,故一组对边平行,一组对角相等的四边形是平行四边形,故①不符合题意;②由“一组对边平行,另一组对边相等”不能判定该四边形为平行四边形,故②符合题意;③由“一组对边平行且相等”可以判定该四边形为平行四边形,故③不符合题意;④一组对边平行,一条对角线被另一条对角线平分,可利用全等得出这组对边也相等,可判定该四边形为平行四边形,故④不符合题意,故选B.
2.【答案】D 3.【答案】A
4.【答案】对角线互相平分的四边形是平行四边形
5.【答案】1;2
6.【答案】8
解:过E点作EG∥PD交AB于G,过D点作DH∥PF交AC于H,∵PD∥AC,PE∥AB,∴PD∥HF,PE∥DG,∴四边形DGEP和四边形DPFH都为平行四边形,∴EG=DP,PE=GD,PF=DH.又∵△ABC是等边三角形,EG∥AC,∴△BEG为等边三角形,∴EG=PD=GB,同理可证
DH=PF=AD,∴PD+PE+PF=BG+GD+AD=AB=8.
7.【答案】平行;2;2
8.【答案】证明:∵AB=DC,AD=CB,
∴四边形ABCD是平行四边形.
∴AB∥CD,
∴∠F=∠E.
【培优提升】
1.【答案】C
解:∵四边形ABCD为平行四边形,∴AD∥
BC,AD=BC.∵AE=CF,∴DE=BF,∴四边形AECF和四边形DEBF都是平行四边形,∴AF∥CE,BE∥DF,∴四边形EMFN也是平行四边形.故除四边形ABCD之外的平行四边形有3个,选C.21cnjy.com
2.【答案】A
解:A中由于所给已知条件只有角的关系,三角形边之间没有等量关系,不能证明三角形全等或边之间平行,也就无法证明四边形EFGH是平行四边形.21教育名师原创作品
3.【答案】C
解:甲正确,乙错误,理由是:在甲的作法中,∵正五边形的每个内角的度数是=108°,AB=BC=CD=DE=AE,∴∠DEC=∠
DCE=×(180°-108°)=36°,同理∠CBD=∠CDB=36°,∴∠ABP=∠
AEP=108°-36°=72°,∴∠BPE=360°-108°-72°-72°=108°=∠
A,∴四边形ABPE是平行四边形,即甲正确;在乙的作法中,∵∠
BAE=108°,∴∠BAM=∠EAM=54°,∵AB=AE=AP,∴∠ABP=∠
APB=×(180°-54°)=63°,∠AEP=∠APE=63°,∴∠
BPE=360°-108°-63°-63°≠108°,即∠ABP=∠AEP,∠BAE≠∠
BPE,∴四边形ABPE不是平行四边形,即乙错误.故选C.
4.【答案】A
5.【答案】B
解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE.∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD.∵DG⊥AF,∴AG=GF=AF.又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2.在Rt△ADG中,根据勾股定理得AG=,则AF=2AG=2.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF.在△ADF和△ECF中,21世纪教育网版权所有
,
∴△ADF≌△ECF,∴AF=EF,则AE=2AF=4.故选B.
6.【答案】80°
解:如图,延长DE交AB于F.
∵AB∥CD,BC∥DE,∴四边形BCDF为平行四边形,∴∠BFD=∠C=120°,
∴∠AFE=60°,∴∠AED=∠A+∠AFE=80°.
7.【答案】1
解:由平行四边形的性质和题干要求,可知D点的纵坐标一定是5;
又由A点相对于B点向左移动了3个单位长度,故可得点D的横坐标为5-3=2,即顶点D的坐标为(2,5);再由B点相对于A点向右移动了3个单位长度,故可得点D的横坐标为5+3=8,即顶点D的坐标为(8,5).故答案为(2,5)或(8,5).www.21-cn-jy.com
9.证明:∵四边形ABCD是平行四边形,∴AD??BC.
∵F是BC中点,∴FC=BC.
又∵DE=AD,∴FC=DE,
又∵DE∥FC,
∴四边形CEDF是平行四边形.
10.解:能实现.方法一:如图①所示.
连结对角线AC,BD交于点O,
过点A,C分别作BD的平行线,过点B,D分别作AC的平行线,
四条平行线依次交于M,N,G,H四点,
则可得四边形MNGH、四边形AODH、四边形AOBM、四边形BOCN、四边形OCGD均为平行四边形.2-1-c-n-j-y
在?AODH中,AO=HD,AH=OD,AD=AD,
∴△AHD≌△DOA,
∴S△AHD=S△AOD,同理S△COD=S△CGD,S△BOC=S△BNC,S△AOB=S△AMB,
∴S?MNGH=2S四边形ABCD.故?MNGH即为所求.
方法二:如图②.连结AC,分别过点B、D作EF∥AC,DH∥AC;延长DC交EF于点F.过点A作EH∥DF交EF于点E,交DH于点H,易知四边形AEFC、四边形ACDH、四边形EFDH均为平行四边形,且S?ACFE=2S△ABC,S?ACDH=2S△ACD,故S?EFDH=2S四边形ABCD.即?EFDH为扩建后的图形.【来源:21·世纪·教育·网】
