19.2.2 菱形的判定 同步练习
文档属性
| 名称 | 19.2.2 菱形的判定 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-08 22:43:10 | ||
图片预览


文档简介
19.2.2 菱形的判定
基础训练
1. 四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC
C.AB=BC D.AC=BD
2.如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60°
3.下列条件不能确定菱形的形状和大小的是( )
A.已知菱形的两条对角线长
B.已知菱形的一条边长和一个内角的度数
C.已知菱形的四条边长
D.已知菱形的周长和面积
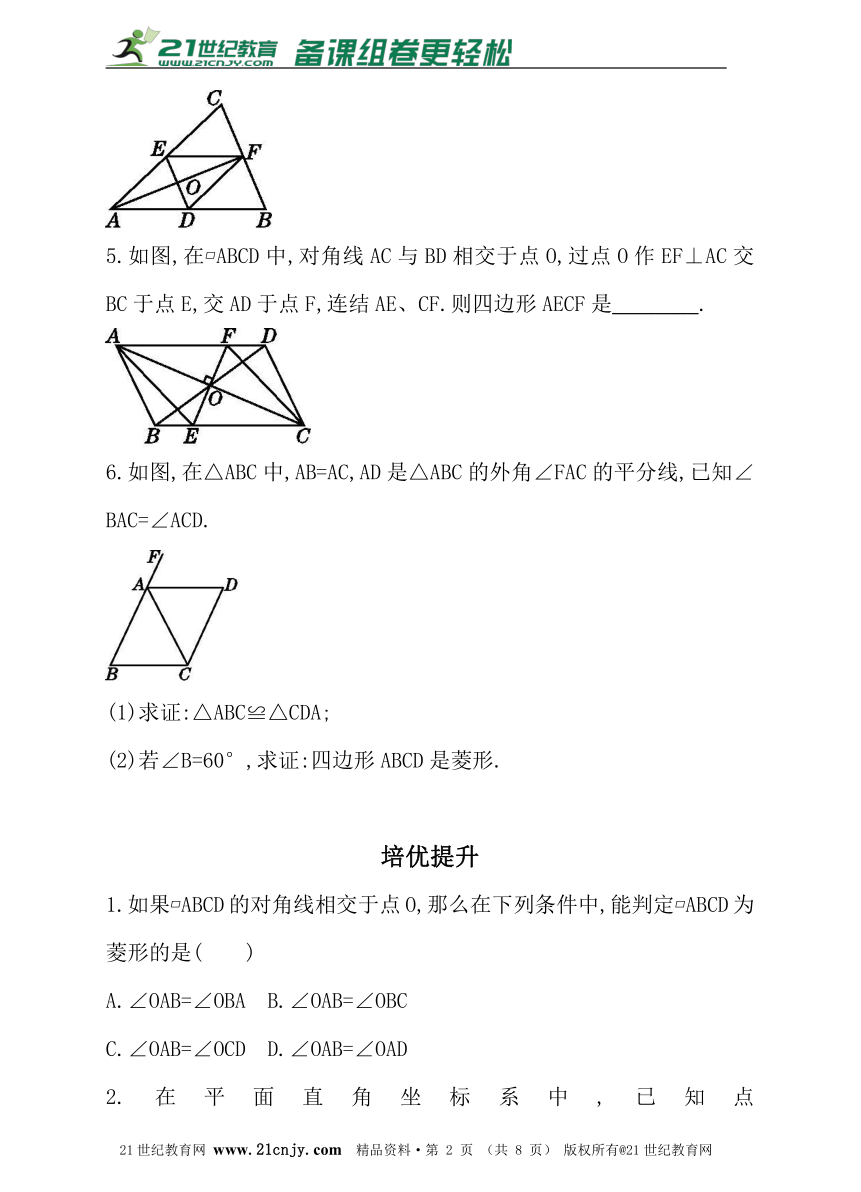
4.如图,将等腰三角形ABC沿AF折叠,使点B与点C重合,展开后,再沿DE折叠,使点A与点F重合,展开后,四边形ADFE是 .
5.如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连结AE、CF.则四边形AECF是________.
6.如图,在△ABC中,AB=AC,AD是△ABC的外角∠FAC的平分线,已知∠BAC=∠ACD.
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
培优提升
1.如果?ABCD的对角线相交于点O,那么在下列条件中,能判定?ABCD为菱形的是( )
A.∠OAB=∠OBA B.∠OAB=∠OBC
C.∠OAB=∠OCD D.∠OAB=∠OAD
2.在平面直角坐标系中,已知点A(0,2),B(-2,0),C(0,-2),D(2,0),则以这四个点为顶点的四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
3.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连结AC,作AC的垂直平分线MN,分别交AD、AC、BC于M、O、N,连结AN、CM,则四边形ANCM是菱形.乙:分别作∠A、∠B的平分线AE、BF,分别交BC、AD于E、F,连结EF,则四边形ABEF是菱形.根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
4. 如图,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,AE交DF于点O,若AB=9,CE=4,AE=8,则DF等于( )
A.4 B.8 C.6 D.9
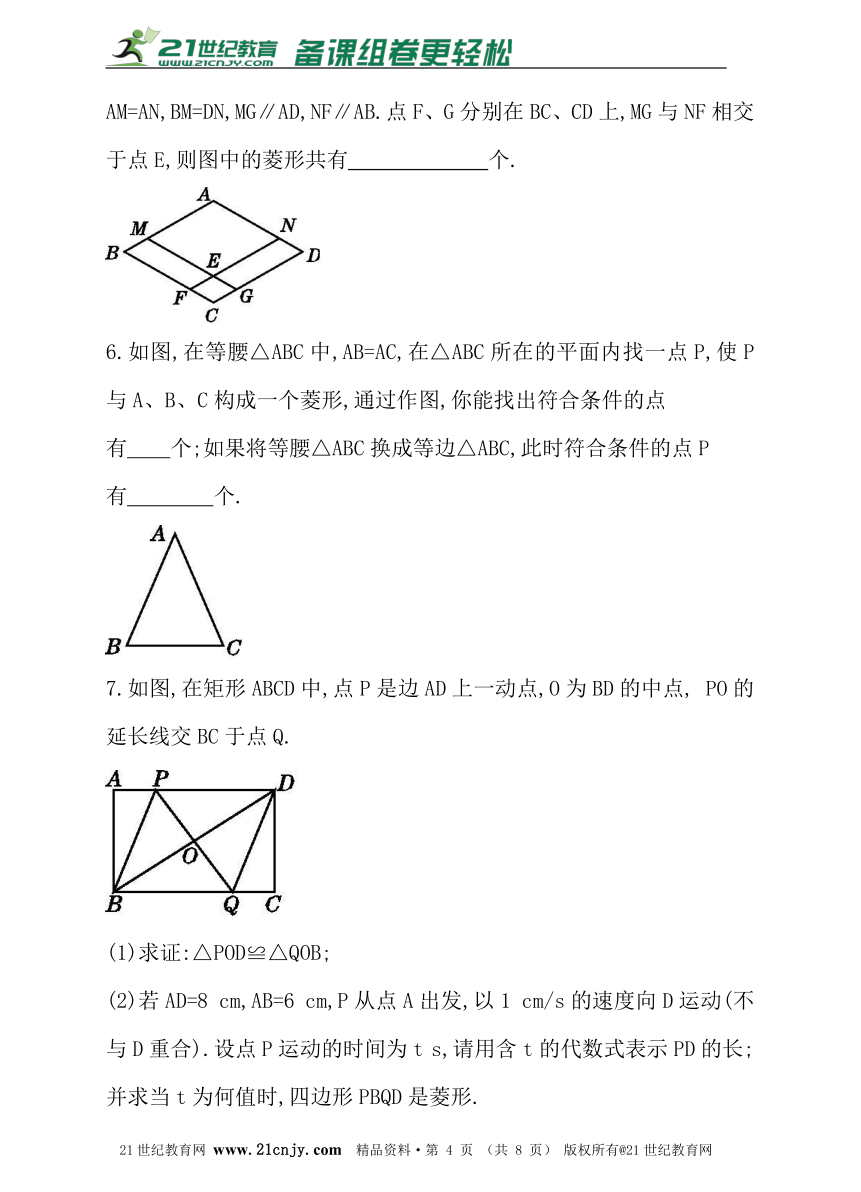
5.如图,四边形ABCD是平行四边形,点M、N分别在AB、AD上,且AM=AN,BM=DN,MG∥AD,NF∥AB.点F、G分别在BC、CD上,MG与NF相交于点E,则图中的菱形共有_____________个.?
6.如图,在等腰△ABC中,AB=AC,在△ABC所在的平面内找一点P,使P与A、B、C构成一个菱形,通过作图,你能找出符合条件的点
有 个;如果将等腰△ABC换成等边△ABC,此时符合条件的点P
有 个.
7.如图,在矩形ABCD中,点P是边AD上一动点,O为BD的中点, PO的延长线交BC于点Q.
(1)求证:△POD≌△QOB;
(2)若AD=8 cm,AB=6 cm,P从点A出发,以1 cm/s的速度向D运动(不与D重合).设点P运动的时间为t s,请用含t的代数式表示PD的长;并求当t为何值时,四边形PBQD是菱形.
8.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连结DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求的值.
参考答案
【基础训练】
1.【答案】C
解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
若AB=BC,则四边形ABCD是菱形.故选C.
2.【答案】A
解:∵将△ABC沿BC方向平移得到△DCE,∴AB∥CD且AB=CD,∴四边形ABCD为平行四边形.当AB=BC时,平行四边形ABCD是菱形.故选A.
3.【答案】C 4.【答案】菱形
5.【答案】菱形
6.证明:(1)∵AB=AC,∴∠B=∠ACB,
∴∠FAC=∠B+∠ACB=2∠ACB.∵AD平分∠FAC,∴∠FAC=2∠CAD,∴∠CAD=∠ACB.
在△ABC和△CDA中,
∴△ABC≌△CDA.
(2)由(1)知∠CAD=∠ACB,
∴AD∥BC.又∵∠BAC=∠ACD,
∴AB∥CD,
∴四边形ABCD是平行四边形.
∵∠B=60°,AB=AC,∴△ABC是等边三角形,
∴AB=BC.
∴平行四边形ABCD是菱形.
【培优提升】
1.【答案】D
解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠OAB=∠ACD.若∠OAB=∠OAD,则∠DAC=∠DCA,∴AD=CD,∴?ABCD是菱形.故选D.
2.【答案】B 3.【答案】C
4.【答案】C
解:∵AB∥CD,∴∠EAF=∠AED.又∵AE是∠DAB的平分线,∴∠DAE=∠EAF,∴∠DAE=∠AED,∴AD=ED.∵AB∥CD,EF∥AD∥BC,∴四边形ADEF和四边形BCEF是平行四边形,∵AD=ED,∴四边形ADEF是菱形.∴AD=AF=9-4=5,AO= AE=4,AE⊥DF.∴DF=2DO=2×=6.故选C.
5.【答案】3
解:∵AM=AN,BM=DN,
∴AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
又∵AM=AN,∴四边形AMEN是菱形,同理可得四边形EFCG是菱形.
∴图中的菱形共有 3个.
6.【答案】1;3
7.(1)证明:∵ 四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO.∵O为BD的中点,∴OD=OB.又∵∠POD=∠QOB,
∴△POD≌△QOB.
(2)解:由(1)知△POD≌△QOB,
∴PD=QB.
又∵PD∥QB,∴四边形PBQD是平行四边形.由题意可得PD=(8-t) cm,当四边形PBQD是菱形时,PB=PD=(8-t) cm.
∵四边形ABCD是矩形,∴∠A=90°,在Rt△ABP中,
AP2+AB2=BP2,∴t2+62=(8-t)2,
解得t=,即当t=时,四边形PBQD是菱形.
8.(1)证明:如图,由对称性得:∠1=∠2,ED=EF,GD=GF.
∵FG∥CD,∴∠1=∠3,则∠2=∠3,∴FE=FG,
(方法一)∴ED=EF=GD=GF,
∴四边形DEFG为菱形.
(方法二)∴ED=FG.又∵ED∥FG,
∴四边形DEFG为平行四边形.
又∵GD=GF,∴四边形DEFG为菱形.
(2)解:设DE=x,则FE=DE=x,EC=8-x,
在Rt△EFC中,FC2+EC2=EF2,即42+(8-x)2=x2.
解得:x=5,∴CE=8-x=3.
∴=.
基础训练
1. 四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
A.AB=CD B.AD=BC
C.AB=BC D.AC=BD
2.如图,将△ABC沿BC方向平移得到△DCE,连结AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60°
3.下列条件不能确定菱形的形状和大小的是( )
A.已知菱形的两条对角线长
B.已知菱形的一条边长和一个内角的度数
C.已知菱形的四条边长
D.已知菱形的周长和面积
4.如图,将等腰三角形ABC沿AF折叠,使点B与点C重合,展开后,再沿DE折叠,使点A与点F重合,展开后,四边形ADFE是 .
5.如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连结AE、CF.则四边形AECF是________.
6.如图,在△ABC中,AB=AC,AD是△ABC的外角∠FAC的平分线,已知∠BAC=∠ACD.
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
培优提升
1.如果?ABCD的对角线相交于点O,那么在下列条件中,能判定?ABCD为菱形的是( )
A.∠OAB=∠OBA B.∠OAB=∠OBC
C.∠OAB=∠OCD D.∠OAB=∠OAD
2.在平面直角坐标系中,已知点A(0,2),B(-2,0),C(0,-2),D(2,0),则以这四个点为顶点的四边形ABCD是( )
A.矩形 B.菱形 C.正方形 D.梯形
3.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连结AC,作AC的垂直平分线MN,分别交AD、AC、BC于M、O、N,连结AN、CM,则四边形ANCM是菱形.乙:分别作∠A、∠B的平分线AE、BF,分别交BC、AD于E、F,连结EF,则四边形ABEF是菱形.根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
4. 如图,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,AE交DF于点O,若AB=9,CE=4,AE=8,则DF等于( )
A.4 B.8 C.6 D.9
5.如图,四边形ABCD是平行四边形,点M、N分别在AB、AD上,且AM=AN,BM=DN,MG∥AD,NF∥AB.点F、G分别在BC、CD上,MG与NF相交于点E,则图中的菱形共有_____________个.?
6.如图,在等腰△ABC中,AB=AC,在△ABC所在的平面内找一点P,使P与A、B、C构成一个菱形,通过作图,你能找出符合条件的点
有 个;如果将等腰△ABC换成等边△ABC,此时符合条件的点P
有 个.
7.如图,在矩形ABCD中,点P是边AD上一动点,O为BD的中点, PO的延长线交BC于点Q.
(1)求证:△POD≌△QOB;
(2)若AD=8 cm,AB=6 cm,P从点A出发,以1 cm/s的速度向D运动(不与D重合).设点P运动的时间为t s,请用含t的代数式表示PD的长;并求当t为何值时,四边形PBQD是菱形.
8.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连结DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求的值.
参考答案
【基础训练】
1.【答案】C
解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
若AB=BC,则四边形ABCD是菱形.故选C.
2.【答案】A
解:∵将△ABC沿BC方向平移得到△DCE,∴AB∥CD且AB=CD,∴四边形ABCD为平行四边形.当AB=BC时,平行四边形ABCD是菱形.故选A.
3.【答案】C 4.【答案】菱形
5.【答案】菱形
6.证明:(1)∵AB=AC,∴∠B=∠ACB,
∴∠FAC=∠B+∠ACB=2∠ACB.∵AD平分∠FAC,∴∠FAC=2∠CAD,∴∠CAD=∠ACB.
在△ABC和△CDA中,
∴△ABC≌△CDA.
(2)由(1)知∠CAD=∠ACB,
∴AD∥BC.又∵∠BAC=∠ACD,
∴AB∥CD,
∴四边形ABCD是平行四边形.
∵∠B=60°,AB=AC,∴△ABC是等边三角形,
∴AB=BC.
∴平行四边形ABCD是菱形.
【培优提升】
1.【答案】D
解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠OAB=∠ACD.若∠OAB=∠OAD,则∠DAC=∠DCA,∴AD=CD,∴?ABCD是菱形.故选D.
2.【答案】B 3.【答案】C
4.【答案】C
解:∵AB∥CD,∴∠EAF=∠AED.又∵AE是∠DAB的平分线,∴∠DAE=∠EAF,∴∠DAE=∠AED,∴AD=ED.∵AB∥CD,EF∥AD∥BC,∴四边形ADEF和四边形BCEF是平行四边形,∵AD=ED,∴四边形ADEF是菱形.∴AD=AF=9-4=5,AO= AE=4,AE⊥DF.∴DF=2DO=2×=6.故选C.
5.【答案】3
解:∵AM=AN,BM=DN,
∴AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
又∵AM=AN,∴四边形AMEN是菱形,同理可得四边形EFCG是菱形.
∴图中的菱形共有 3个.
6.【答案】1;3
7.(1)证明:∵ 四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO.∵O为BD的中点,∴OD=OB.又∵∠POD=∠QOB,
∴△POD≌△QOB.
(2)解:由(1)知△POD≌△QOB,
∴PD=QB.
又∵PD∥QB,∴四边形PBQD是平行四边形.由题意可得PD=(8-t) cm,当四边形PBQD是菱形时,PB=PD=(8-t) cm.
∵四边形ABCD是矩形,∴∠A=90°,在Rt△ABP中,
AP2+AB2=BP2,∴t2+62=(8-t)2,
解得t=,即当t=时,四边形PBQD是菱形.
8.(1)证明:如图,由对称性得:∠1=∠2,ED=EF,GD=GF.
∵FG∥CD,∴∠1=∠3,则∠2=∠3,∴FE=FG,
(方法一)∴ED=EF=GD=GF,
∴四边形DEFG为菱形.
(方法二)∴ED=FG.又∵ED∥FG,
∴四边形DEFG为平行四边形.
又∵GD=GF,∴四边形DEFG为菱形.
(2)解:设DE=x,则FE=DE=x,EC=8-x,
在Rt△EFC中,FC2+EC2=EF2,即42+(8-x)2=x2.
解得:x=5,∴CE=8-x=3.
∴=.
