2.2.3运用乘法公式进行计算同步练习
图片预览

文档简介
湘教版版七年级下册数学2.2.3运用乘法公式进行计算同步练习
一、选择题(本大题共8小题)
1. 若a2+ab+b2+A=(a-b) 2,则A式应为( )
A.ab B.-3ab C.0 D.-2ab
2. 如果a2-b2=4,那么(a+b)2(a-b)2的结果是( )
A.32 B.16 C.8 D.4
3. 计算(a+1)2(a-1)2的结果是( )
A.a4-1 B.a4+1 C.a4+2a2+1 D.a4-2a2+1
4. 计算(m-2n-1)(m+2n-1)的结果为( )
A.m2-4n2-2m+1 B.m2+4n2-2m+1
C.m2-4n2-2m-1 D.m2+4n2+2m-1
5. 若一个正方形的边长增加3 cm,它的面积增加45 cm2,则此正方形原来的边长为( )
A.6 cm B.9 cm C.12 cm D.无法确定2·1·c·n·j·y
6.计算(2a+3b)2(2a-3b) 2的结果是( )
A.4a2-9b2 B.16a4-72a2b2+81b4
C.(4a2-9b2)2 D.4a4-12a2b2+9b4
7. 设正方形的面积为S1 cm2,长方形的面积为S2 cm2,如果长方形的长比正方形的边长多3 cm,宽比正方形的边长少3 cm.那么S1与S2的大小关系是( )www-2-1-cnjy-com
A.S1>S2 B.S1<S2 C.S1=S2 D.不能确定
8.由m(a+b+c)=ma+mb+mc,可得:(a+b)(a2-ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,即:(a+b)(a2-ab+b2)=a3+b3.①【出处:21教育名师】
我们把等式①叫做多项式乘法的立方公式.
下列应用这个立方公式进行的变形不正确的是( )
A.(a+1)(a2+a+1)=a3+1 B.(2x+y)(4x2-2xy+y2)=8x3+y3
C.(a+3)(a2-3a+9)=a3+27 D.(x+4y)(x2-4xy+16y2)=x3+64y3
二、填空题(本大题共6小题)
9. 已知a-b=3,则a(a-2b)+b2的值为 .
10.计算(-3x+2y-z)(3x+2y+z)= .
11. 下图是四张全等的矩形纸片拼成的图形,请利用图中的空白部分面积的不同表示方法,写出一个关于a,b的恒等式:__________________.21教育网
12. 已知a+b=2,ab=1,则a2+b2的值是 .
13. 已知a2+b2+4a-2b+5=0,则的值是__________.
14. 下图由边长为a和b的两个正方形组成,通过用不同的方法,计算图中阴影部分的面积,可以验证的一个乘法公式是____________________.2-1-c-n-j-y
三、计算题(本大题共4小题)
15. 计算:(1)(3x+2y)(3x-2y);
(2)(-m+n)(-m-n);
(3)(-2x-3)(2x-3).
16. 先化简,再求值:5(m+n)(m-n)-2(m+n)2-3(m-n)2,其中m=-2,n=.
17. 一个正方形的边长增加3 cm,它的面积就增加39 cm2,这个正方形的边长是多少?
18. 计算:(2+1)(22+1)(24+1)(28+1)…(22n+1)的值.
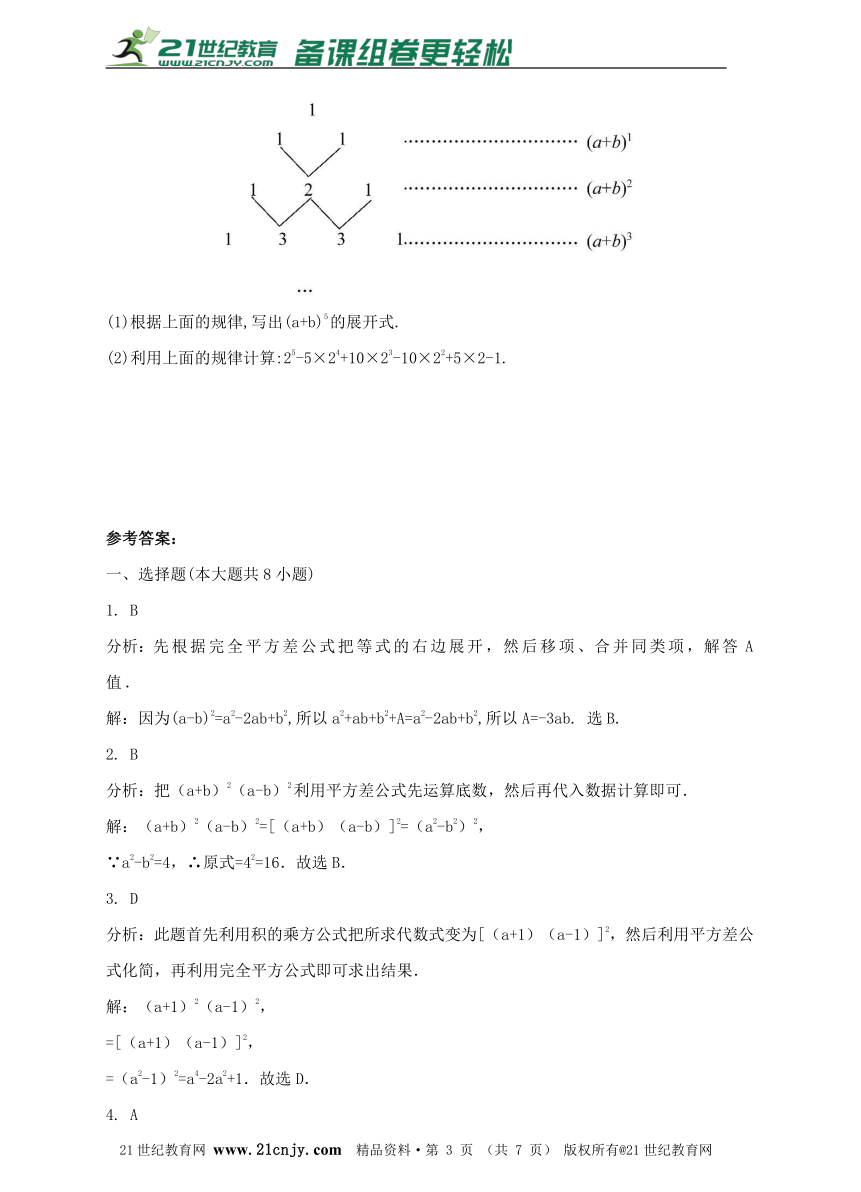
19. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.21·cn·jy·com
(1)根据上面的规律,写出(a+b)5的展开式.
(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:先根据完全平方差公式把等式的右边展开,然后移项、合并同类项,解答A值.
解:因为(a-b)2=a2-2ab+b2,所以a2+ab+b2+A=a2-2ab+b2,所以A=-3ab. 选B.
2. B
分析:把(a+b)2(a-b)2利用平方差公式先运算底数,然后再代入数据计算即可.
解:(a+b)2(a-b)2=[(a+b)(a-b)]2=(a2-b2)2,
∵a2-b2=4,∴原式=42=16.故选B.
3. D
分析:此题首先利用积的乘方公式把所求代数式变为[(a+1)(a-1)]2,然后利用平方差公式化简,再利用完全平方公式即可求出结果.21*cnjy*com
解:(a+1)2(a-1)2,
=[(a+1)(a-1)]2,
=(a2-1)2=a4-2a2+1.故选D.
4. A
分析:采用整体思想将(m-1)看成整体利用平方差计算即可。
解: (m-2n-1)(m+2n-1)
=[(m-1)-2n][(m-1)+2n]
=(m-1)2-4n2
=m2-2m+1-4n2
=m2-4n2-2m+1. 选A.
5.A
分析:利用方程思想求边长即可。
解:设此正方形原来的边长为x,则x2+45=(x+3)2,
∴(x+3+x)(x+3-x)=45,
∴x=6,故选A.
6B
分析:先利用平方差公式再利用完全平方公式解答即可。
解: (2a+3b)2(2a-3b)2
=[(2a+3b)(2a-3b)]2
=(4a2-9b2)2
=16a4-72a2b2+81b4. 选B.
7. A
分析:利用方程思想和面积公式可解答。
解; 设正方形边长为x,
可得长方形长为x+3,宽为x-3,
得出S1=x2,S2=(x+3)(x-3)=x2-9,
∴S1>S2,故选A.
8.A
分析:本题需先根据多项式乘法的立方公式分别对每一项进行计算,即可得出答案.
解:解:A、(a+1)(a2+a+1)=a3+2a2+2a+1,故本选项错误;
B、(2x+y)(4x2-2xy+y2)=8x3+y3,故本选项正确;
C、(a+3)(a2-3a+9)=a3+27,故本选项正确;
D、(x+4y)(x2-4xy+16y2)=x3+64y3,故本选项正确.故选A.
二、填空题(本大题共6小题)
9.分析:先将原式化简,然后将a-b=1整体代入求解。
解:a(a-2b)+b2=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.答案:9
10.分析:将(3x+z)看成一个整体利用平方差进行计算即可。
解:(-3x+2y-z)(3x+2y+z)
=[2y-(3x+z)][2y+(3x+z)]
=4y2-(3x+z)2
=4y2-9x2-6xz-z2.答案:4y2-9x2-6xz-z2
11. 分析:根据图中的面积写一个恒等式,需要用两种方法表示空白正方形的面积.首先观察大正方形是由四个矩形和一个空白正方形组成,所以空白正方形的面积等于大正方形的面积减去四个矩形的面积,即(a+b)2-4ab,空白正方形的面积也等于它的边长的平方,即(a-b)2,根据面积相等有(a+b)2-4ab=(a-b)2.21cnjy.com
解:(a+b)2-4ab=(a-b)2
12.分析:利用完全平方公式有(a+b)2=a2+2ab+b2,把2ab移到等式的左边,可得(a+b)2-2ab=a2+b2,然后代入求值即可.www.21-cn-jy.com
解:∵(a+b)2=a2+2ab+b2,∴a2+b2=(a+b)2-2aB.∵a+b=2,ab=1,∴a2+b2=22-2×1=2.21·世纪*教育网
13.分析:原等式可化为(a2+4a+4)+(b2-2b+1)=0,即(a+2)2+(b-1)2=0,根据非负数的特点知a+2=0且b-1=0,从而可知a=-2且b=1.然后将其代入求的值即可.
解:
14. 分析:要表示阴影部分的面积,可以从两个方面出发:一是观察阴影部分是由边长为a的正方形除去边长为b的正方形得到的,所以它的面积等于a2-b2;二是阴影部分是由两个直角梯形构成的,所以它的面积又等于两个梯形的面积之和.这两个梯形的面积都等于(b+a)(a-b),所以梯形的面积和是(a+b)(a-b),根据阴影部分的面积不变,得(a+b)(a-b)=a2-b2.因此验证的一个乘法公式是(a+b)(a-b)=a2-b2.【来源:21cnj*y.co*m】
解:(a+b)(a-b)=a2-b2
三、计算题(本大题共4小题)
15.
分析:(1)本题符合平方差公式的结构特征,其中3x对应“a”,2y对应“b”;(2)题中相同项为-m,互为相反数的项为n与-n,故本题也符合平方差公式的结构特征;(3)利用加法交换律将【来源:21·世纪·教育·网】
原式变形为(-3+2x)(-3-2x),然后运用平方差公式计算.
解:(1)(3x+2y)(3x-2y)=(3x)2-(2y)2=9x2-4y2.
(2)(-m+n)(-m-n)=(-m)2-n2.
(3)(-2x-3)(2x-3)= (-3+2x)(-3-2x)=(-3)2-(2x)2=9-4x2.
16.解:5(m+n)(m-n)-2(m+n)2-3(m-n)2=5(m2-n2)-2(m2+2mn+n2)-3(m2-2mn+n2)=5m2-5n2-2m2-4mn-2n2-3m2+6mn-3n2=-10n2+2mn.当m=-2,n=时,原式=-10n2+2mn=-10×2+2×(-2)×=-.【版权所有:21教育】
17.分析:如果设原正方形的边长为x cm,根据题意和正方形的面积公式可列出方程(x+3)2=x2+39,求解即可.21教育名师原创作品
解:设原正方形的边长为x cm,则(x+3)2=x2+39,
即x2+6x+9=x2+39,解得x=5(cm).
故这个正方形的边长是5 cm.
18.分析:为了能便于运用平方差公式,观察到待求式中都是和的形式,没有差的形式,可设法构造出差的因数,于是可乘以(2-1),这样就可巧妙地运用平方差公式了.
解:(2+1)(22+1)(24+1)(28+1)…(22n+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(22n+1)
=(22-1)(22+1)(24+1)(28+1)…(22n+1)
=(24-1)(24+1)(28+1)…(22n+1)
=…=(22n-1)(22n+1)=24n-1.
19. 解:解:(1)∵(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a4+4a3b+6a2b2+4ab3+b4,
∴(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5,
故答案为:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2)25-5×24+10×23-10×22+5×2-1=(2-1)5=15=1(根据(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5的逆运用得出的),21世纪教育网版权所有
故答案为:1.
一、选择题(本大题共8小题)
1. 若a2+ab+b2+A=(a-b) 2,则A式应为( )
A.ab B.-3ab C.0 D.-2ab
2. 如果a2-b2=4,那么(a+b)2(a-b)2的结果是( )
A.32 B.16 C.8 D.4
3. 计算(a+1)2(a-1)2的结果是( )
A.a4-1 B.a4+1 C.a4+2a2+1 D.a4-2a2+1
4. 计算(m-2n-1)(m+2n-1)的结果为( )
A.m2-4n2-2m+1 B.m2+4n2-2m+1
C.m2-4n2-2m-1 D.m2+4n2+2m-1
5. 若一个正方形的边长增加3 cm,它的面积增加45 cm2,则此正方形原来的边长为( )
A.6 cm B.9 cm C.12 cm D.无法确定2·1·c·n·j·y
6.计算(2a+3b)2(2a-3b) 2的结果是( )
A.4a2-9b2 B.16a4-72a2b2+81b4
C.(4a2-9b2)2 D.4a4-12a2b2+9b4
7. 设正方形的面积为S1 cm2,长方形的面积为S2 cm2,如果长方形的长比正方形的边长多3 cm,宽比正方形的边长少3 cm.那么S1与S2的大小关系是( )www-2-1-cnjy-com
A.S1>S2 B.S1<S2 C.S1=S2 D.不能确定
8.由m(a+b+c)=ma+mb+mc,可得:(a+b)(a2-ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,即:(a+b)(a2-ab+b2)=a3+b3.①【出处:21教育名师】
我们把等式①叫做多项式乘法的立方公式.
下列应用这个立方公式进行的变形不正确的是( )
A.(a+1)(a2+a+1)=a3+1 B.(2x+y)(4x2-2xy+y2)=8x3+y3
C.(a+3)(a2-3a+9)=a3+27 D.(x+4y)(x2-4xy+16y2)=x3+64y3
二、填空题(本大题共6小题)
9. 已知a-b=3,则a(a-2b)+b2的值为 .
10.计算(-3x+2y-z)(3x+2y+z)= .
11. 下图是四张全等的矩形纸片拼成的图形,请利用图中的空白部分面积的不同表示方法,写出一个关于a,b的恒等式:__________________.21教育网
12. 已知a+b=2,ab=1,则a2+b2的值是 .
13. 已知a2+b2+4a-2b+5=0,则的值是__________.
14. 下图由边长为a和b的两个正方形组成,通过用不同的方法,计算图中阴影部分的面积,可以验证的一个乘法公式是____________________.2-1-c-n-j-y
三、计算题(本大题共4小题)
15. 计算:(1)(3x+2y)(3x-2y);
(2)(-m+n)(-m-n);
(3)(-2x-3)(2x-3).
16. 先化简,再求值:5(m+n)(m-n)-2(m+n)2-3(m-n)2,其中m=-2,n=.
17. 一个正方形的边长增加3 cm,它的面积就增加39 cm2,这个正方形的边长是多少?
18. 计算:(2+1)(22+1)(24+1)(28+1)…(22n+1)的值.
19. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.21·cn·jy·com
(1)根据上面的规律,写出(a+b)5的展开式.
(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.
参考答案:
一、选择题(本大题共8小题)
1. B
分析:先根据完全平方差公式把等式的右边展开,然后移项、合并同类项,解答A值.
解:因为(a-b)2=a2-2ab+b2,所以a2+ab+b2+A=a2-2ab+b2,所以A=-3ab. 选B.
2. B
分析:把(a+b)2(a-b)2利用平方差公式先运算底数,然后再代入数据计算即可.
解:(a+b)2(a-b)2=[(a+b)(a-b)]2=(a2-b2)2,
∵a2-b2=4,∴原式=42=16.故选B.
3. D
分析:此题首先利用积的乘方公式把所求代数式变为[(a+1)(a-1)]2,然后利用平方差公式化简,再利用完全平方公式即可求出结果.21*cnjy*com
解:(a+1)2(a-1)2,
=[(a+1)(a-1)]2,
=(a2-1)2=a4-2a2+1.故选D.
4. A
分析:采用整体思想将(m-1)看成整体利用平方差计算即可。
解: (m-2n-1)(m+2n-1)
=[(m-1)-2n][(m-1)+2n]
=(m-1)2-4n2
=m2-2m+1-4n2
=m2-4n2-2m+1. 选A.
5.A
分析:利用方程思想求边长即可。
解:设此正方形原来的边长为x,则x2+45=(x+3)2,
∴(x+3+x)(x+3-x)=45,
∴x=6,故选A.
6B
分析:先利用平方差公式再利用完全平方公式解答即可。
解: (2a+3b)2(2a-3b)2
=[(2a+3b)(2a-3b)]2
=(4a2-9b2)2
=16a4-72a2b2+81b4. 选B.
7. A
分析:利用方程思想和面积公式可解答。
解; 设正方形边长为x,
可得长方形长为x+3,宽为x-3,
得出S1=x2,S2=(x+3)(x-3)=x2-9,
∴S1>S2,故选A.
8.A
分析:本题需先根据多项式乘法的立方公式分别对每一项进行计算,即可得出答案.
解:解:A、(a+1)(a2+a+1)=a3+2a2+2a+1,故本选项错误;
B、(2x+y)(4x2-2xy+y2)=8x3+y3,故本选项正确;
C、(a+3)(a2-3a+9)=a3+27,故本选项正确;
D、(x+4y)(x2-4xy+16y2)=x3+64y3,故本选项正确.故选A.
二、填空题(本大题共6小题)
9.分析:先将原式化简,然后将a-b=1整体代入求解。
解:a(a-2b)+b2=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.答案:9
10.分析:将(3x+z)看成一个整体利用平方差进行计算即可。
解:(-3x+2y-z)(3x+2y+z)
=[2y-(3x+z)][2y+(3x+z)]
=4y2-(3x+z)2
=4y2-9x2-6xz-z2.答案:4y2-9x2-6xz-z2
11. 分析:根据图中的面积写一个恒等式,需要用两种方法表示空白正方形的面积.首先观察大正方形是由四个矩形和一个空白正方形组成,所以空白正方形的面积等于大正方形的面积减去四个矩形的面积,即(a+b)2-4ab,空白正方形的面积也等于它的边长的平方,即(a-b)2,根据面积相等有(a+b)2-4ab=(a-b)2.21cnjy.com
解:(a+b)2-4ab=(a-b)2
12.分析:利用完全平方公式有(a+b)2=a2+2ab+b2,把2ab移到等式的左边,可得(a+b)2-2ab=a2+b2,然后代入求值即可.www.21-cn-jy.com
解:∵(a+b)2=a2+2ab+b2,∴a2+b2=(a+b)2-2aB.∵a+b=2,ab=1,∴a2+b2=22-2×1=2.21·世纪*教育网
13.分析:原等式可化为(a2+4a+4)+(b2-2b+1)=0,即(a+2)2+(b-1)2=0,根据非负数的特点知a+2=0且b-1=0,从而可知a=-2且b=1.然后将其代入求的值即可.
解:
14. 分析:要表示阴影部分的面积,可以从两个方面出发:一是观察阴影部分是由边长为a的正方形除去边长为b的正方形得到的,所以它的面积等于a2-b2;二是阴影部分是由两个直角梯形构成的,所以它的面积又等于两个梯形的面积之和.这两个梯形的面积都等于(b+a)(a-b),所以梯形的面积和是(a+b)(a-b),根据阴影部分的面积不变,得(a+b)(a-b)=a2-b2.因此验证的一个乘法公式是(a+b)(a-b)=a2-b2.【来源:21cnj*y.co*m】
解:(a+b)(a-b)=a2-b2
三、计算题(本大题共4小题)
15.
分析:(1)本题符合平方差公式的结构特征,其中3x对应“a”,2y对应“b”;(2)题中相同项为-m,互为相反数的项为n与-n,故本题也符合平方差公式的结构特征;(3)利用加法交换律将【来源:21·世纪·教育·网】
原式变形为(-3+2x)(-3-2x),然后运用平方差公式计算.
解:(1)(3x+2y)(3x-2y)=(3x)2-(2y)2=9x2-4y2.
(2)(-m+n)(-m-n)=(-m)2-n2.
(3)(-2x-3)(2x-3)= (-3+2x)(-3-2x)=(-3)2-(2x)2=9-4x2.
16.解:5(m+n)(m-n)-2(m+n)2-3(m-n)2=5(m2-n2)-2(m2+2mn+n2)-3(m2-2mn+n2)=5m2-5n2-2m2-4mn-2n2-3m2+6mn-3n2=-10n2+2mn.当m=-2,n=时,原式=-10n2+2mn=-10×2+2×(-2)×=-.【版权所有:21教育】
17.分析:如果设原正方形的边长为x cm,根据题意和正方形的面积公式可列出方程(x+3)2=x2+39,求解即可.21教育名师原创作品
解:设原正方形的边长为x cm,则(x+3)2=x2+39,
即x2+6x+9=x2+39,解得x=5(cm).
故这个正方形的边长是5 cm.
18.分析:为了能便于运用平方差公式,观察到待求式中都是和的形式,没有差的形式,可设法构造出差的因数,于是可乘以(2-1),这样就可巧妙地运用平方差公式了.
解:(2+1)(22+1)(24+1)(28+1)…(22n+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(22n+1)
=(22-1)(22+1)(24+1)(28+1)…(22n+1)
=(24-1)(24+1)(28+1)…(22n+1)
=…=(22n-1)(22n+1)=24n-1.
19. 解:解:(1)∵(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
(a+b)4=a4+4a3b+6a2b2+4ab3+b4,
∴(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5,
故答案为:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2)25-5×24+10×23-10×22+5×2-1=(2-1)5=15=1(根据(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5的逆运用得出的),21世纪教育网版权所有
故答案为:1.
