18.2.2菱形的性质(1)课件
图片预览








文档简介
课件33张PPT。一起放飞理想的翅膀
在知识的天空中自由翱翔
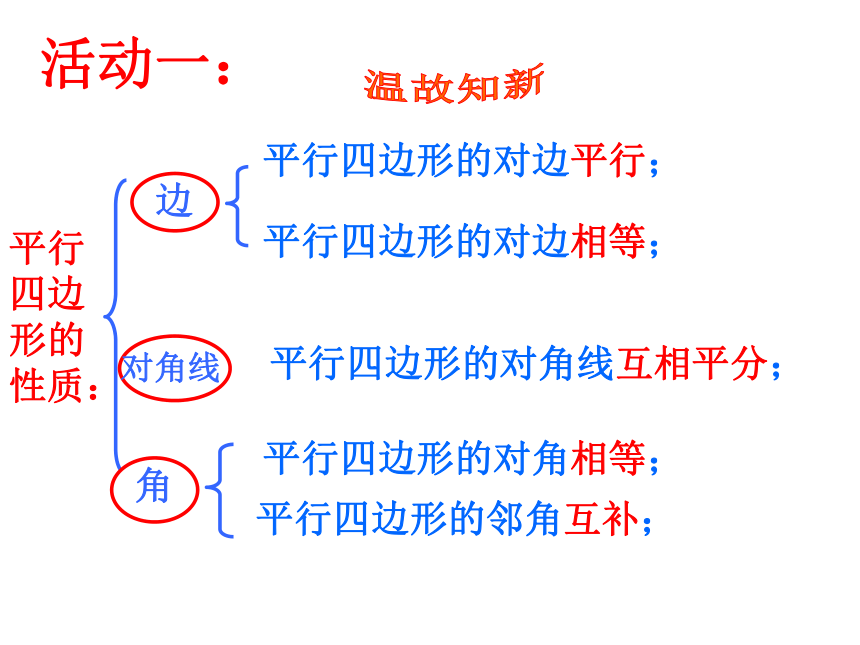
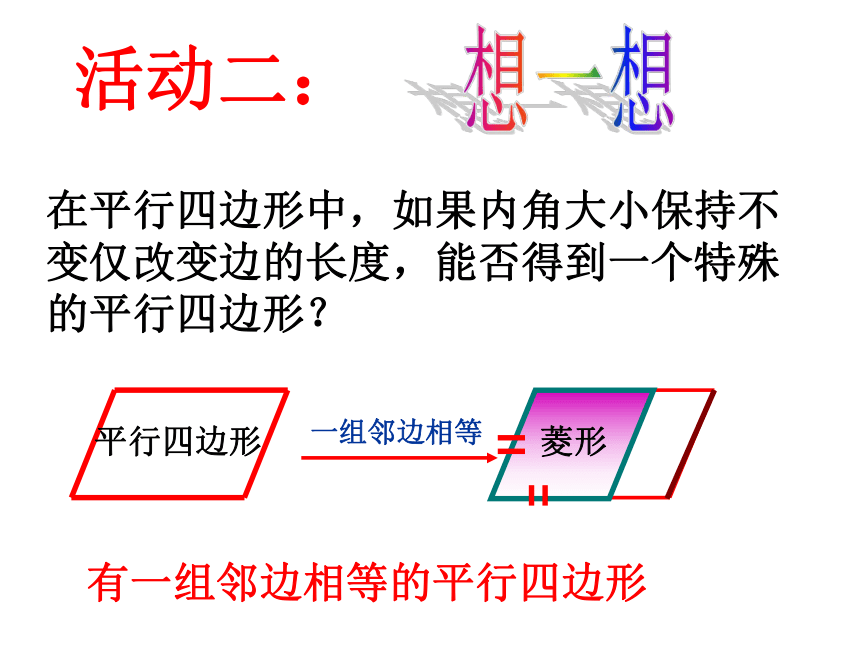
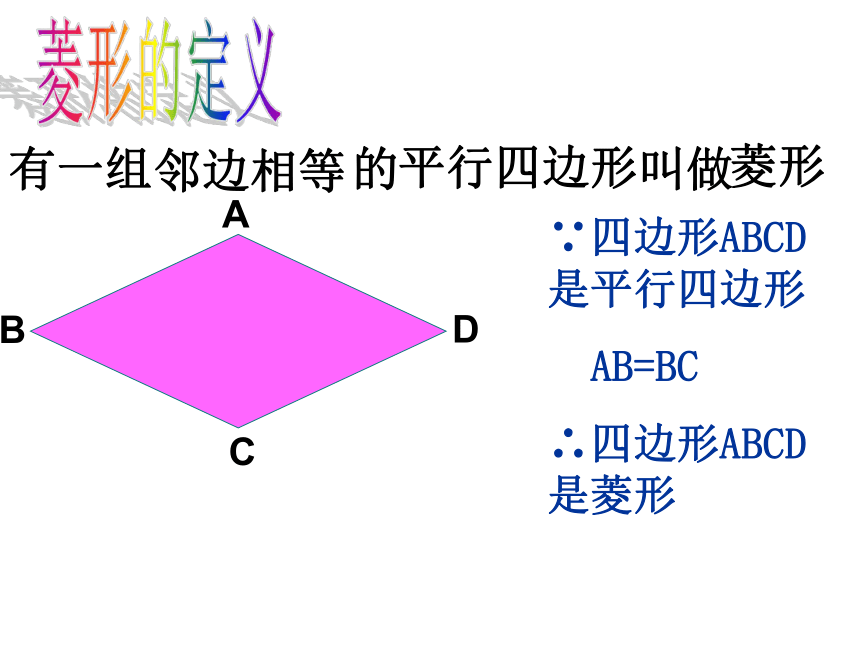
18.2特殊的平行四边形18.2.2菱形的性质(1)平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新活动一:矩形的性质矩形的四个角都是直角矩形的对角线相等想一想在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形? 平行四边形 菱形活动二:菱形的定义有一组 的 叫做邻边相等 平行四边形 ADCB∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形菱形 菱形的性质菱形的对边平行且相等.菱形的对角相等.菱形是特殊的平行四边形,它具有平行四边形的一切性质.即菱形的对角线互相平分.
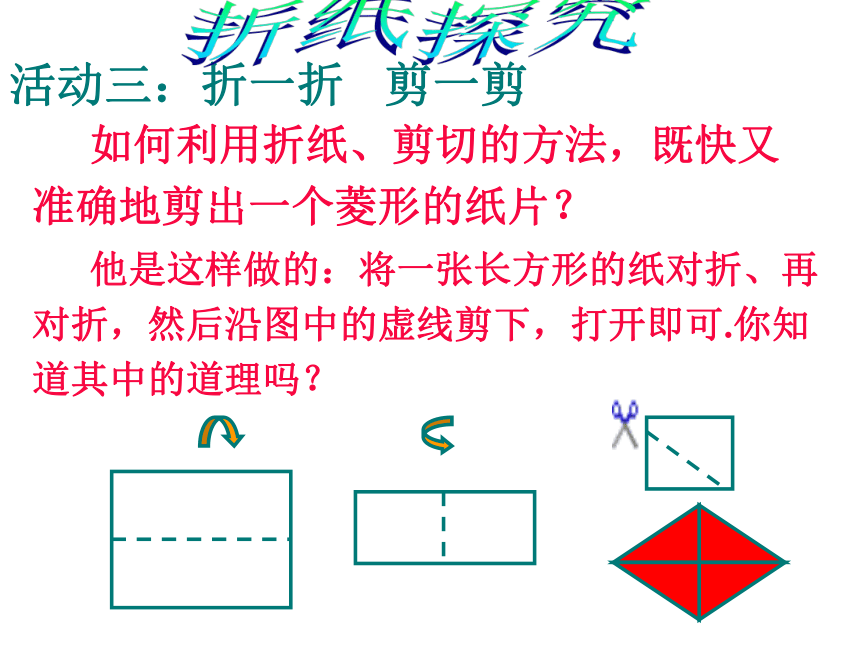
菱形是中心对称图形,对角线的交点是对称中心.感受生活你能举出生活中你看到的菱形吗?生活感受菱形就在我们身边三菱汽车标志欣赏感受生活 他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?活动三:折一折 剪一剪折纸探究菱形的性质①、菱形的四边在数量上有什么关系?;
②、菱形是轴对称图形吗?如果是,那么谁是对称轴?
③、菱形的对角线在位置上有什么关系?
④、菱形的每一条对角线是否平分一组对角?相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:菱形ABCD中AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678探究菱形的性质菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的四条边相等菱形是轴对称图形,也是中心对称图形
已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中,又∵AO=CO∴DB⊥AC,
DB平分∠ADC(三线合一)同理: DB平分∠ABC;
AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB BD平分∠ADC和∠ABC求证:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;菱形的性质1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
解:活动四:做一做菱形的面积公式S菱形=底×高=对角线乘积的一半S菱形=2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )生活中的数学生活中的数学练一练1.菱形的定义: 是菱形
2.菱形的性质:①菱形的四条边 ,
②菱形的对角线 ,并且每一条对角线------一组对角.
3.下列说法不正确的有 (填序号)
①菱形的对边平行且相等.②菱形的对角线互相平分
③菱形的对角线相等.④菱形的对角线互相垂直.
⑤菱形的一条对角线平分一组对角.⑥菱形的对角相等.
4.菱形的面积公式:① ② .
5.菱形既是 图形,又是 图形. 活动五:练一练3cm600C练一练9.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度有关菱形问题可转化为直角三角形或等腰三角形的问题来解决3.菱形的两条对角线的长分别为6cm和8cm,那么菱形的面积是_____. 24cm2 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言活动六:菱形的性质从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形是中心对称图形,也是轴对称图形;
知识再现菱形的性质③菱形的四边都相等;
④菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
知识再现知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:P60页第5题
P61页第11,12题作业布置:如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想谢谢光临指导再见画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:1、菱形是轴对称图形吗?2、菱形有几条对称轴?3、对称轴之间有什么关系?4、你能看出图中哪些线段和角相等?
在知识的天空中自由翱翔
18.2特殊的平行四边形18.2.2菱形的性质(1)平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新活动一:矩形的性质矩形的四个角都是直角矩形的对角线相等想一想在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形? 平行四边形 菱形活动二:菱形的定义有一组 的 叫做邻边相等 平行四边形 ADCB∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形菱形 菱形的性质菱形的对边平行且相等.菱形的对角相等.菱形是特殊的平行四边形,它具有平行四边形的一切性质.即菱形的对角线互相平分.
菱形是中心对称图形,对角线的交点是对称中心.感受生活你能举出生活中你看到的菱形吗?生活感受菱形就在我们身边三菱汽车标志欣赏感受生活 他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?活动三:折一折 剪一剪折纸探究菱形的性质①、菱形的四边在数量上有什么关系?;
②、菱形是轴对称图形吗?如果是,那么谁是对称轴?
③、菱形的对角线在位置上有什么关系?
④、菱形的每一条对角线是否平分一组对角?相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:菱形ABCD中AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678探究菱形的性质菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
菱形的四条边相等菱形是轴对称图形,也是中心对称图形
已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中,又∵AO=CO∴DB⊥AC,
DB平分∠ADC(三线合一)同理: DB平分∠ABC;
AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB BD平分∠ADC和∠ABC求证:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;菱形的性质1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
解:活动四:做一做菱形的面积公式S菱形=底×高=对角线乘积的一半S菱形=2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.1m2 )生活中的数学生活中的数学练一练1.菱形的定义: 是菱形
2.菱形的性质:①菱形的四条边 ,
②菱形的对角线 ,并且每一条对角线------一组对角.
3.下列说法不正确的有 (填序号)
①菱形的对边平行且相等.②菱形的对角线互相平分
③菱形的对角线相等.④菱形的对角线互相垂直.
⑤菱形的一条对角线平分一组对角.⑥菱形的对角相等.
4.菱形的面积公式:① ② .
5.菱形既是 图形,又是 图形. 活动五:练一练3cm600C练一练9.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度有关菱形问题可转化为直角三角形或等腰三角形的问题来解决3.菱形的两条对角线的长分别为6cm和8cm,那么菱形的面积是_____. 24cm2 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言活动六:菱形的性质从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形是中心对称图形,也是轴对称图形;
知识再现菱形的性质③菱形的四边都相等;
④菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
知识再现知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:P60页第5题
P61页第11,12题作业布置:如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想谢谢光临指导再见画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:1、菱形是轴对称图形吗?2、菱形有几条对称轴?3、对称轴之间有什么关系?4、你能看出图中哪些线段和角相等?
