18.2.3正方形的性质(1)课件
图片预览



文档简介
课件24张PPT。18.2.3正方形的性质(1)达连河镇第一中学:汪多敏正方形正方形有一个角是
直角
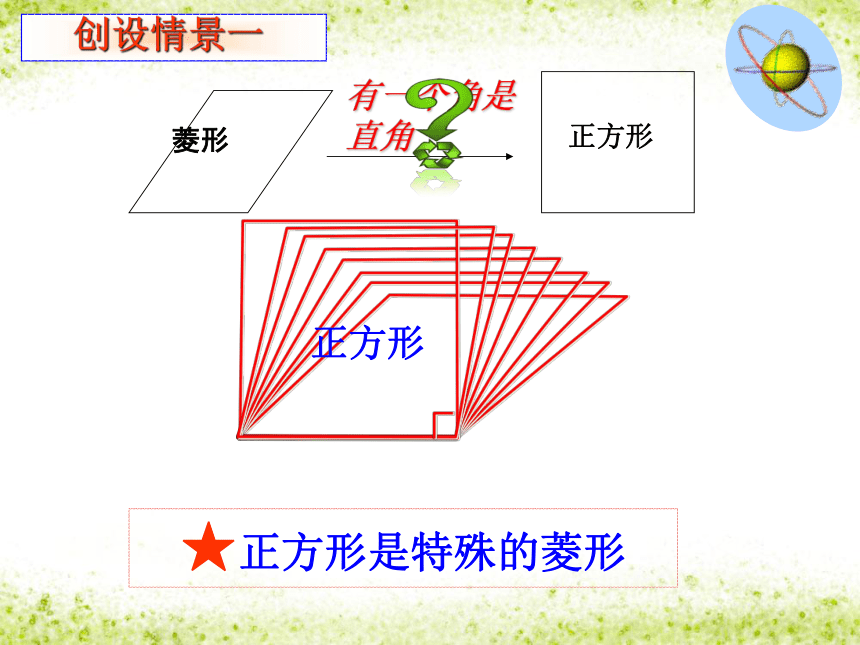
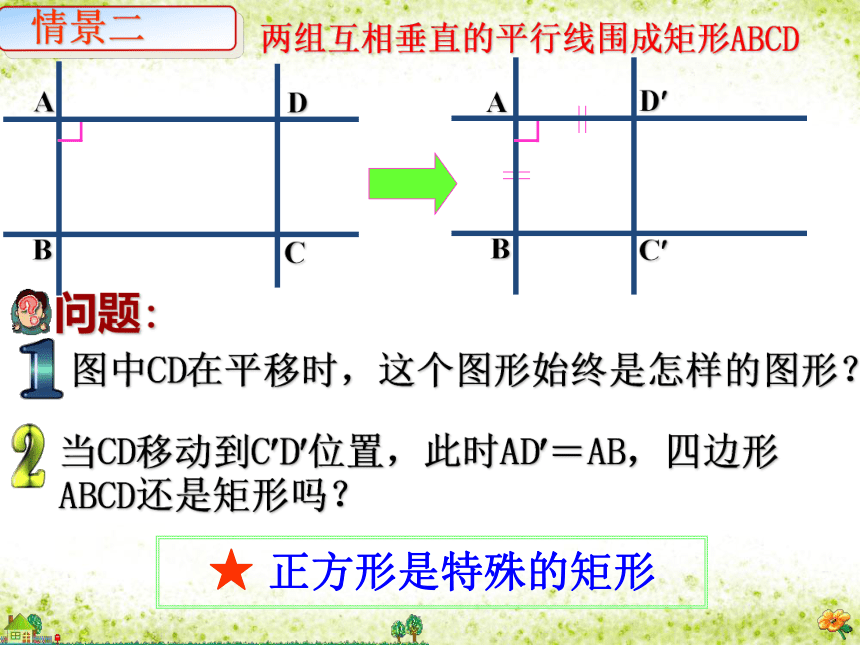
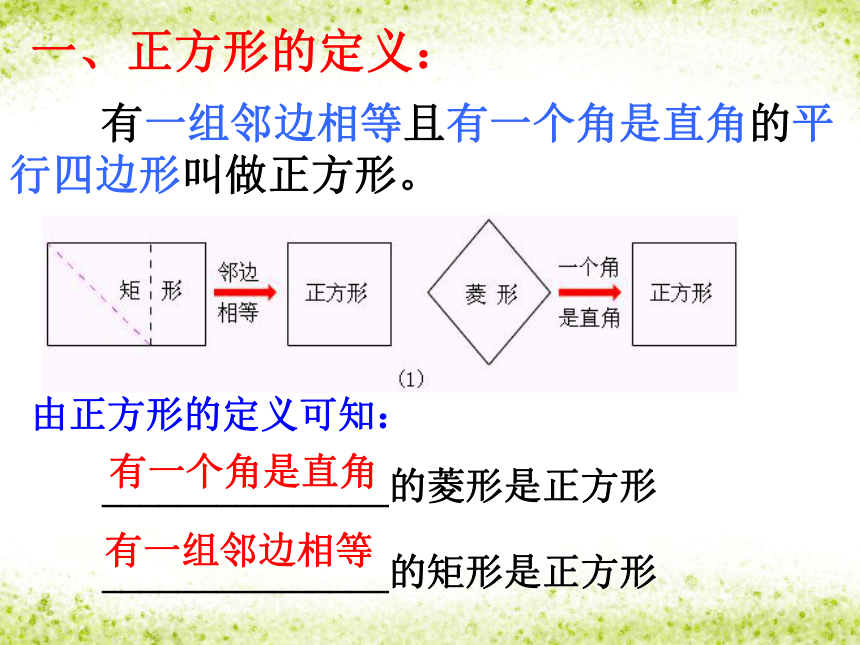
创设情景一★正方形是特殊的菱形AB ★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 一、正方形的定义:_______________的菱形是正方形 _______________的矩形是正方形由正方形的定义可知:有一个角是直角有一组邻边相等四边形
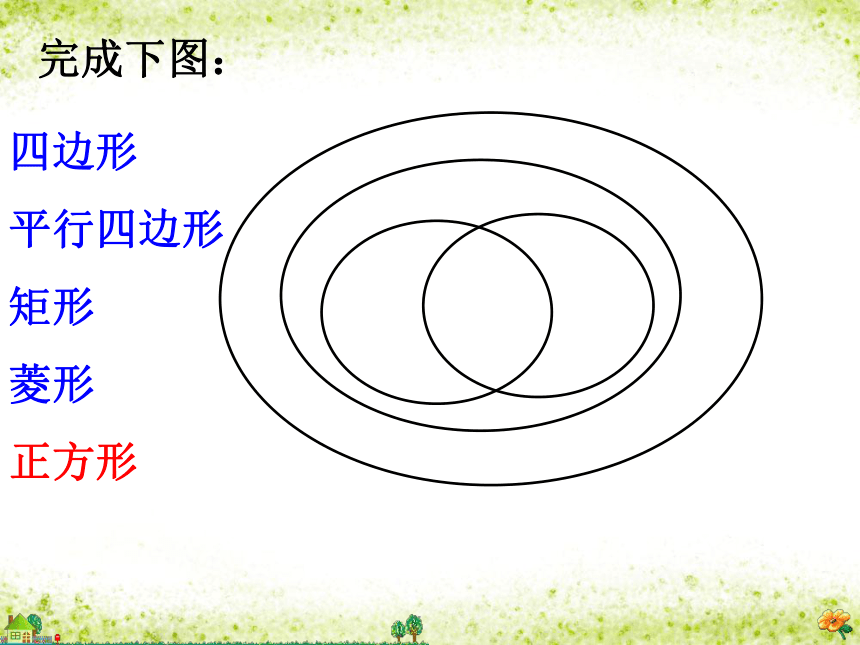
平行四边形
矩形
菱形
正方形完成下图:特殊的平行四边形
特殊的矩形
特殊的菱形
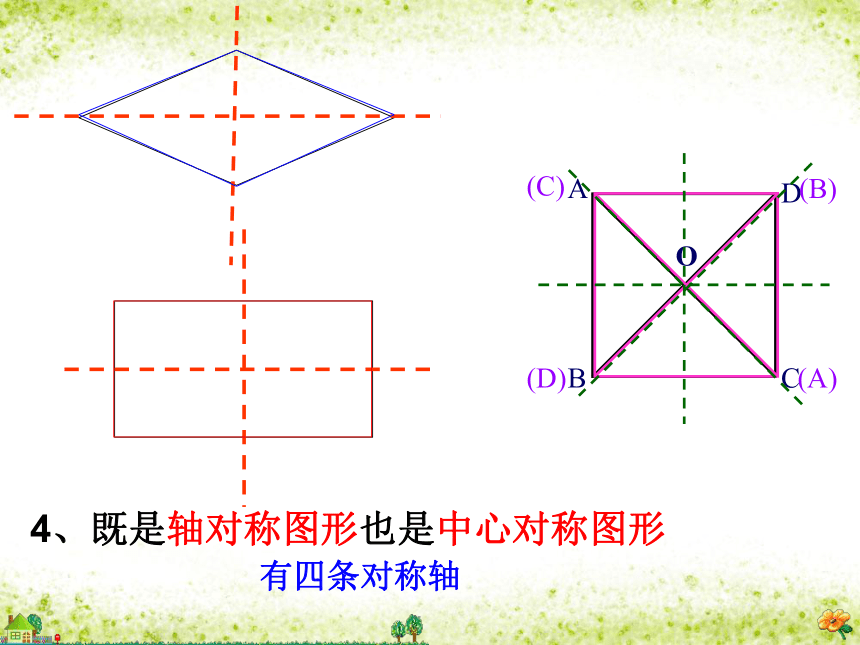
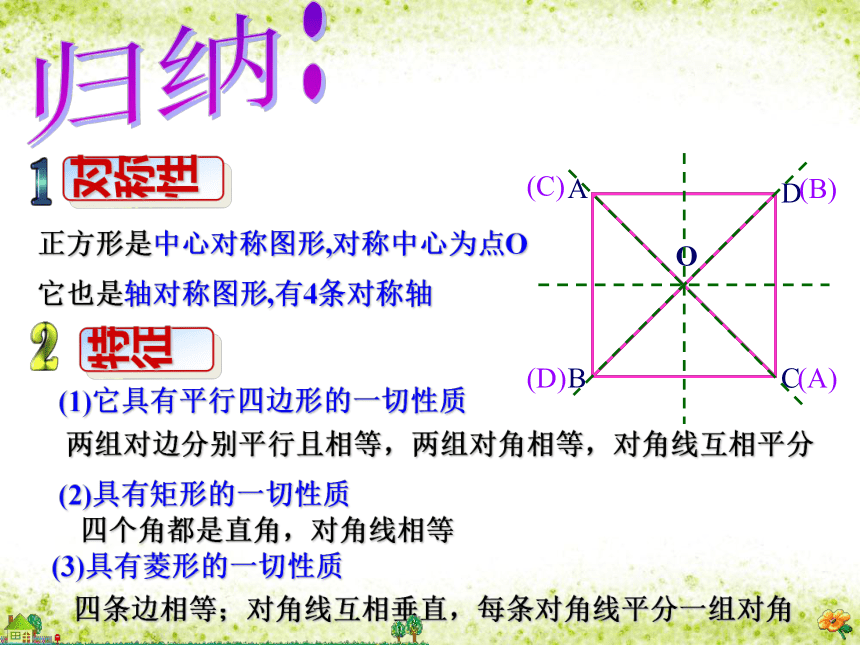
四条边都相等且对边平行;两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.四个角都是直角; 1、边:2. 角:3.对角线:(A)(B)(C)(D)4、既是轴对称图形也是中心对称图形有四条对称轴正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)归纳:例4 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD尝试练习:43624230⑹(7)159、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.16cm510.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是多少?EF证△D0E≌△C0F(ASA)111.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。又∵MN∥AB
∴∠OMN=∠1=
∠BCO=∠ONM=45° ∴OM=ON⌒1⌒2证明:
∵四边形ABCD是正方形 ∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°∴△COM≌△DON(SAS)∴DN=MCH⌒3答:DN=MC DN⊥MC(2)由△COM≌△DON得∠2=∠3又∠3+∠CMO=90°∴∠2+∠CMO=90°∴∠DHM=90°∴DN⊥MC12、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG13.在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.求证:DP=EF证明:连接PB又∵PE⊥AB , PF⊥BC∵四边形ABCD是正方形∴∠ABC=90°,AD=AB,
∠DAP=∠BAP=45°∴∠PEB=∠PFB=90°∴四边形PECF是矩形∴PB=EF又∵AP=AP∴△ADE≌△CDG(SAS)∴PD=PB∴PD=EF14.在正方形ABCD中,P为BC边上一点,Q为CD边上一点,如果PQ=BP+DQ,求∠PAQ的度数.15.如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数。数一数图中正方形的个数,你发现了什么? ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识第十九章 四边形【例1】已知:如图1,正方形ABCD中,对角线的交点为O.
(1)E是AC上的一点,过点A作AG⊥BE于G,AG、BD交于点F.求证:OE=OF.
(2)若点E在AC上的延长线上(如图2),过点A做AG⊥BE交EB的延长线于G,AG的延长线交BD于点F,其它条件不变,OE=OF还成立吗?若成立,请给予证明;若不成立,请说明理由.【解析】(1)要证明OE=OF,只需证明△BOE≌△AOF,要证△BOE≌△AOF,利用正方形性质即可;
第(2)问和第(1)问图形虽然有所变化,但实质一样,也可通过证△BOE≌△AOF,从而得到OE=OF.【例2】已知:如图3,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.【答案】证明:∵PN⊥l1,QM⊥l1,∴PN∥QM,∠PNM=90°∵PQ∥NM,∴四边形PQMN是矩形∵四边形ABCD是正方形∴∠BAD=∠ADC=90°,AB=AD=DC(正方形的四条边都相等,四个角都是直角)∴∠1+∠2=90°,又∠3+∠2=90°,∴∠1=∠3∴△ABM≌△DAN∴AM=DN同理 AN=DP∴AM+AN=DN+DP 即MN=PN.∴四边形PQMN是正方形(有一组邻边相等的矩形是正方形)谢谢!
直角
创设情景一★正方形是特殊的菱形AB ★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。 一、正方形的定义:_______________的菱形是正方形 _______________的矩形是正方形由正方形的定义可知:有一个角是直角有一组邻边相等四边形
平行四边形
矩形
菱形
正方形完成下图:特殊的平行四边形
特殊的矩形
特殊的菱形
四条边都相等且对边平行;两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.四个角都是直角; 1、边:2. 角:3.对角线:(A)(B)(C)(D)4、既是轴对称图形也是中心对称图形有四条对称轴正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)归纳:例4 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD尝试练习:43624230⑹(7)159、正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.16cm510.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两正方形重合部分的面积是多少?EF证△D0E≌△C0F(ASA)111.已知:如图,正方形ABCD的对角线相交于点O,M、N在OB和OC上,且MN∥BC,连结DN、MC,试猜想DN与MC有什么关系?并证明你的猜想。又∵MN∥AB
∴∠OMN=∠1=
∠BCO=∠ONM=45° ∴OM=ON⌒1⌒2证明:
∵四边形ABCD是正方形 ∴OC=OD ,
∠COD=∠COB=90°
∠1=∠BCO=45°∴△COM≌△DON(SAS)∴DN=MCH⌒3答:DN=MC DN⊥MC(2)由△COM≌△DON得∠2=∠3又∠3+∠CMO=90°∴∠2+∠CMO=90°∴∠DHM=90°∴DN⊥MC12、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG13.在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是点E、F.求证:DP=EF证明:连接PB又∵PE⊥AB , PF⊥BC∵四边形ABCD是正方形∴∠ABC=90°,AD=AB,
∠DAP=∠BAP=45°∴∠PEB=∠PFB=90°∴四边形PECF是矩形∴PB=EF又∵AP=AP∴△ADE≌△CDG(SAS)∴PD=PB∴PD=EF14.在正方形ABCD中,P为BC边上一点,Q为CD边上一点,如果PQ=BP+DQ,求∠PAQ的度数.15.如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数。数一数图中正方形的个数,你发现了什么? ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识第十九章 四边形【例1】已知:如图1,正方形ABCD中,对角线的交点为O.
(1)E是AC上的一点,过点A作AG⊥BE于G,AG、BD交于点F.求证:OE=OF.
(2)若点E在AC上的延长线上(如图2),过点A做AG⊥BE交EB的延长线于G,AG的延长线交BD于点F,其它条件不变,OE=OF还成立吗?若成立,请给予证明;若不成立,请说明理由.【解析】(1)要证明OE=OF,只需证明△BOE≌△AOF,要证△BOE≌△AOF,利用正方形性质即可;
第(2)问和第(1)问图形虽然有所变化,但实质一样,也可通过证△BOE≌△AOF,从而得到OE=OF.【例2】已知:如图3,四边形ABCD是正方形,分别过点A、C两点l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点
求证:四边形PQMN是正方形.【答案】证明:∵PN⊥l1,QM⊥l1,∴PN∥QM,∠PNM=90°∵PQ∥NM,∴四边形PQMN是矩形∵四边形ABCD是正方形∴∠BAD=∠ADC=90°,AB=AD=DC(正方形的四条边都相等,四个角都是直角)∴∠1+∠2=90°,又∠3+∠2=90°,∴∠1=∠3∴△ABM≌△DAN∴AM=DN同理 AN=DP∴AM+AN=DN+DP 即MN=PN.∴四边形PQMN是正方形(有一组邻边相等的矩形是正方形)谢谢!
