6.3.2 实数的性质及运算 教学课件
文档属性
| 名称 | 6.3.2 实数的性质及运算 教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 223.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 19:18:55 | ||
图片预览






文档简介
课件15张PPT。6.3 实 数第六章 实 数2 实数的性质及运算1.理解在实数范围内的相反数、倒数、绝对值的意义; (重点)
2.掌握实数的运算法则,熟练地利用计算器去解决有
关实数的运算问题.(重点、难点)学习目标 有理数中的几个重要概念:导入新课回顾与思考思考:无理数也有相反数吗?怎么表示?有绝对值吗?怎么表示?有倒数吗?怎么表示?有理数中的相反数、绝对值、倒数等概念对实数仍然适用. 只有符号不同的两个数叫互为相反数,零
的相反数是零.1. 相反数 3. 倒数 如果两个数的积等于1,这两个数叫互为倒数.
其中一个叫另一个的倒数.讲授新课练一练1. 的相反数是 ,
的相反数是 ,
的相反数是 . 2. -π的绝对值是 ,
= ,
= .
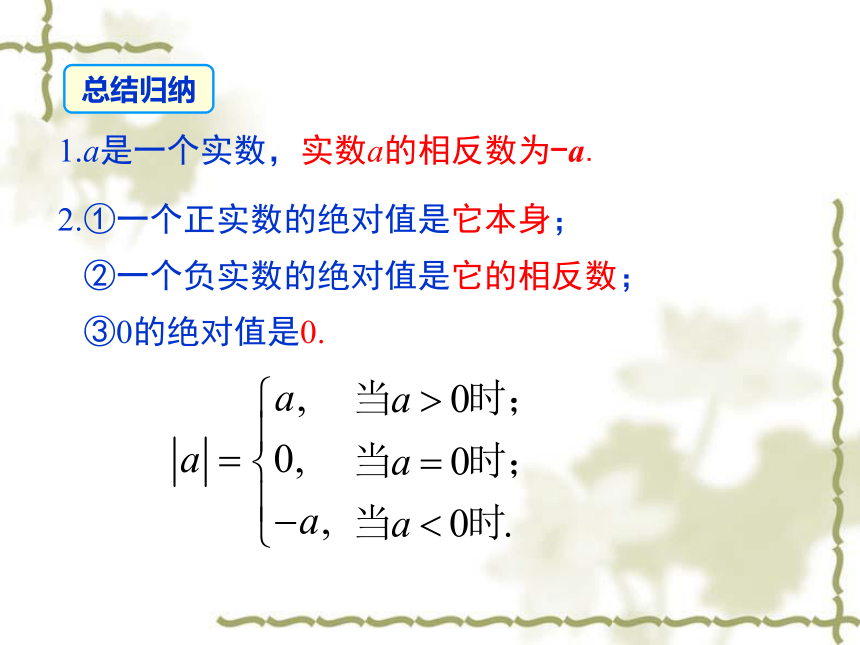
1.a是一个实数,实数a的相反数为-a. 2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.总结归纳典例精析例2 (1)求 的相反数, 当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除、乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算.进行实数运算时,有理数的运算法则及性质等同样适用.实数的运算顺序(1)先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号,则先进行括号里的运算.例3 计算下列各式的值:典例精析例4 计算(结果保留小数点后两位):注意:计算过程中要多保留一位!1.判断:(1) ( )(2) 的绝对值是 ; ( )(3) 的相反数是 . ( )××当堂练习2.下列各数中,互为相反数的是( )
A.3 与 B. 与
C. 与 D. 与C5.- 是 的相反数;π-3.14的相反数是 .3. 的值是( )
A.5 B.-1 C. D.C3.14-π4.比较大小:(1) ;(2) 4.>﹤6.计算(1)(2)(3)=4 通过这节课的学习,你有什么收获?你还有什么疑惑的地方? (2)混合运算中注意两点:一是运算顺序;二是灵活运用运算律简化计算.课堂小结
2.掌握实数的运算法则,熟练地利用计算器去解决有
关实数的运算问题.(重点、难点)学习目标 有理数中的几个重要概念:导入新课回顾与思考思考:无理数也有相反数吗?怎么表示?有绝对值吗?怎么表示?有倒数吗?怎么表示?有理数中的相反数、绝对值、倒数等概念对实数仍然适用. 只有符号不同的两个数叫互为相反数,零
的相反数是零.1. 相反数 3. 倒数 如果两个数的积等于1,这两个数叫互为倒数.
其中一个叫另一个的倒数.讲授新课练一练1. 的相反数是 ,
的相反数是 ,
的相反数是 . 2. -π的绝对值是 ,
= ,
= .
1.a是一个实数,实数a的相反数为-a. 2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.总结归纳典例精析例2 (1)求 的相反数, 当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除、乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算.进行实数运算时,有理数的运算法则及性质等同样适用.实数的运算顺序(1)先算乘方和开方;
(2)再算乘除,最后算加;
(3)如果遇到括号,则先进行括号里的运算.例3 计算下列各式的值:典例精析例4 计算(结果保留小数点后两位):注意:计算过程中要多保留一位!1.判断:(1) ( )(2) 的绝对值是 ; ( )(3) 的相反数是 . ( )××当堂练习2.下列各数中,互为相反数的是( )
A.3 与 B. 与
C. 与 D. 与C5.- 是 的相反数;π-3.14的相反数是 .3. 的值是( )
A.5 B.-1 C. D.C3.14-π4.比较大小:(1) ;(2) 4.>﹤6.计算(1)(2)(3)=4 通过这节课的学习,你有什么收获?你还有什么疑惑的地方? (2)混合运算中注意两点:一是运算顺序;二是灵活运用运算律简化计算.课堂小结
