湖北省枣阳市育才中学2016-2017学年高一下学期第一次质量检测数学试题
文档属性
| 名称 | 湖北省枣阳市育才中学2016-2017学年高一下学期第一次质量检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 788.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-10 09:15:25 | ||
图片预览




文档简介
湖北省枣阳市育才中学2016-2017学年下学期高一年级第一次质量检测数学试题
★祝考试顺利★
时间:120分钟
分值150分_
第I卷(选择题共60分)
一、选择题(本大题12小题,每小题5分,共60分)
1.一个几何体的三视图如图所示,则该几何体的体积的是(
)
(A)
(B)
(C)
(D)
2.
如图,一个不透明圆柱体的正视图和侧视图(
( http: / / www.21cnjy.com )左视图)为两全等的正方形,若将它竖直放在桌面上,则该圆柱体在桌面上从垂直位置旋转到水平位置的过程中,其在水平桌面上的正投影不可能是
(
)
3.设、是两条不同的直线,、是两个不同的平面.
考察下列命题,其中真命题是
A.
B.∥,∥
C.∥
D.
4.如图是正三棱锥V-ABC的正视图、侧视图和俯视图,则其侧视图的面积是(
)
( http: / / www.21cnjy.com )
A.4
B.5
C.6
D.7
5.(2015秋 石景山区期末)某建筑由相同的若干个房间组成,该楼的三视图如图所示,最高一层的房间在什么位置(
)
( http: / / www.21cnjy.com )
A.左前
B.右前
C.左后
D.右后
6.已知正方体的棱长为2,则其外接球的半径为
A. B. C. D.
7.在正四棱锥中,底面正方形的边长为1,侧棱长为2,则异面直线与所成角的大小为(
)
A.
B.
C.
D.
8.已知某几何体的三视图(单位:)如图所示,则该几何体的表面积是(
)
( http: / / www.21cnjy.com )
A.
B.
C.
D.
9.在空间中,下列命题错误的是(
)
A.一条直线与两个平行平面中的一个相交,则必与另一个相交
B.一个平面与两个平行平面相交,交线平行
C.平行于同一平面的两个平面平行
D.平行于同一直线的两个平面平行
10.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为(
)
A.1∶
B.
1∶9
C.
1∶
D.
1∶
11.在三棱锥中,侧面、侧面、侧两两互相垂直,且,设三棱锥的体积为,三棱锥的外接球的体积为,则(
)
A.
B.
C.
D.
12.在正方体中,、分别是、的中点,则异面直线与所成角的大小是(
)
A.
B.
C.
D.
第II卷(非选择题)
二
、填空题(本大题共4个小题,每题5分,满分20分)
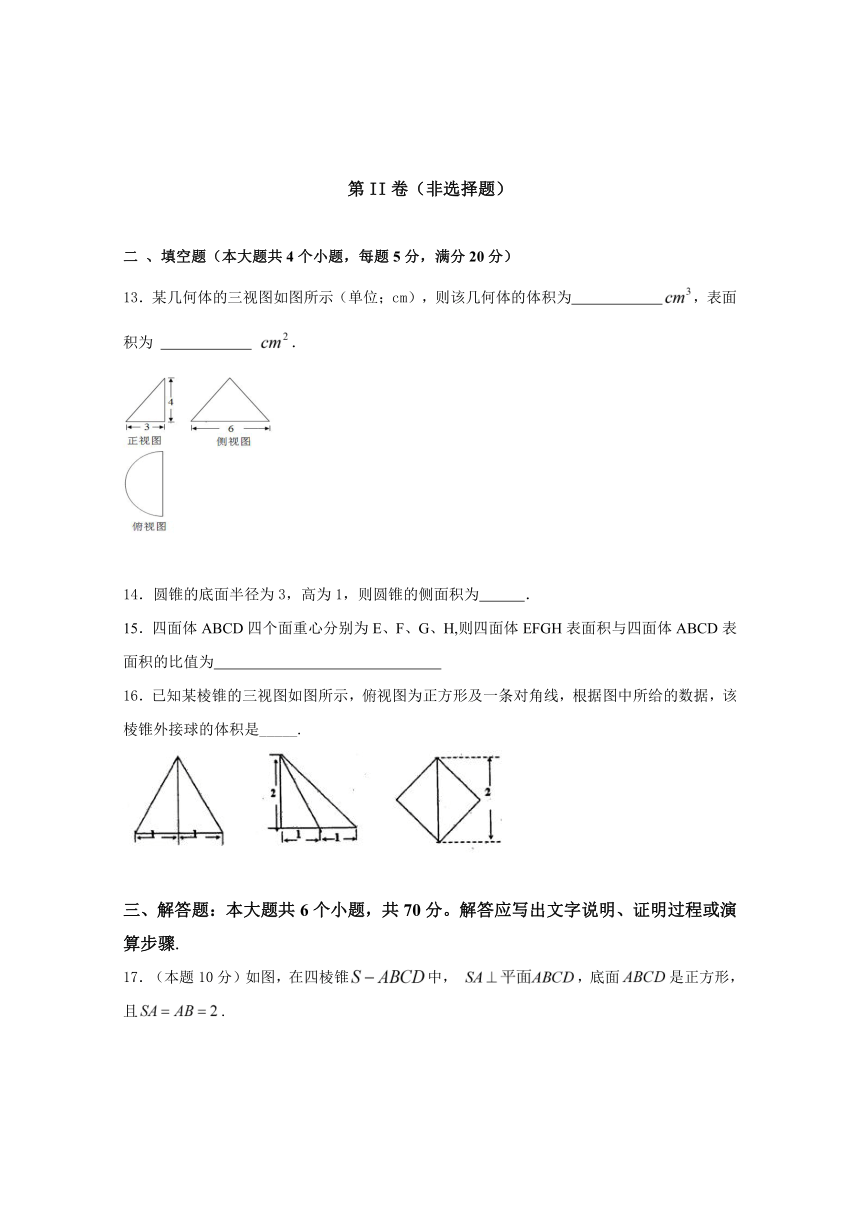
13.某几何体的三视图如图所示(单位;cm),则该几何体的体积为
,表面积为
.
( http: / / www.21cnjy.com )
14.圆锥的底面半径为3,高为1,则圆锥的侧面积为
.
15.四面体ABCD四个面重心分别为E、F
( http: / / www.21cnjy.com )、G、H,则四面体EFGH表面积与四面体ABCD表面积的比值为
16.已知某棱锥的三视图如图所示,俯视图为正方形及一条对角线,根据图中所给的数据,该棱锥外接球的体积是_____.
( http: / / www.21cnjy.com )
三、解答题:本大题共6个小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17.(本题10分)如图,在四棱锥中,
,底面是正方形,且.
( http: / / www.21cnjy.com )
(Ⅰ)若是中点,是的中点,求证:;
(Ⅱ)求四棱锥的侧面积.
18.(本题12分)如图,四棱锥中,
底面是直角梯形,
∥,,,侧面⊥底面,且是以为底的等腰三角形.
( http: / / www.21cnjy.com )
(1)证明:⊥;
(2)若三棱锥的体积等于,问:是否存
在过点的平面,分别交、于点,使得平面∥平面?若存在,求出的面积;若不存在,请说明理由.
19.(本题12分)在如图所示的四棱锥中,
四边形为正方形,
平面,且、、分别为、、的中点,.
( http: / / www.21cnjy.com )
(1)证明:平面;
(2)若,求二面角的余弦值.
20.(本题12分)如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4,AB=2,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
21.(本题12分)(本小题满分12分)如图所示多面体中,⊥平面,为平行四边形,分别为的中点,,,.
(1)求证:∥平面;
(2)若∠=90°,求证;
(3)若∠=120°,求该多面体的体积.
( http: / / www.21cnjy.com )
22.(本题12分)
如图1,已知矩形中,,分别是的中点,对角线与交于点,沿将矩形折起,使平面与平面所成角为60°,在图2中:
( http: / / www.21cnjy.com )
(1)求证:;
(2)求平面与平面所成角的余弦值。
答案
选择:1_5ABBCC
6_10
DDCDD
11_12
AD
填空:13.,.
14.
15.1:9
16.
17.(Ⅰ)证明见解析;(Ⅱ).
试题解析:(Ⅰ)证明:取的中点,连结.
( http: / / www.21cnjy.com )
因为是三角形的中位线,
所以.
又因为,所以.
所以四边形是平行四边形,所以,
又因为,,所以.
(Ⅱ)依题意得.
因为所以,
又因为,且,所以.
又因为,所以.
所以是直角三角形.
,所以.
同理可得.
所以四棱锥的侧面积是.
考点:直线与平面平行的判定定理;直线与平面垂直的判定定理;棱锥的侧面积。
18.(1)证明见解析;(2)存在,且面积为.
试题分析:(1)要证明线线垂直,可以通过线面垂直来证明,取中点,连,即证明平面.利用侧面⊥底面和在底面解三角形即可证明;(2)由三棱锥的体积,求出,取中点,中点,连得平面平面,取中点,.
试题解析:(1)取中点,连
∵为等腰三角形,
∴
在直角梯形中,由,,
得,
则为正三角形,∴
∴平面,⊥.
(2)由(1)知,又平面底面
∴平面
则,∴
取中点,中点,连
由
可知平面平面
取中点,∴
考点:空间立体几何证明平行与垂直.
19.(1)详见解析(2)
试题解析:(1)证明:连结分别交、于点、连结、为中点,
为中点,,
又为中点,
又为的中点,
平面平面平面.
( http: / / www.21cnjy.com )
(2)平面,又平面.如图,
以
为坐标原点,
所在直线分别为轴,轴,轴建立空间直角坐标系,
设,可知,则,平面,平面的一个法向量,设平面的法向量为,则,
即,令,则,,
由图可知,
二面角为钝角,
二面角的余弦值为.
( http: / / www.21cnjy.com )
`
20.(1)证明见解析;(2)证明见解析;(3).
试题分析:(1)因为分别是,的中点,由三角形的中位线性质知,∥,从而证明∥平面;(2)由题意易知,,又,所以,故,所以由线面垂直的判定定理可得结论;(3)可转化为到平面的距离的倍,再利用三棱锥的等体积法求到平面的距离.
试题解析:(1)因为AB∥EM,且AB=EM,所以四边形ABEM为平行四边形.
连接AE,则AE过点P,且P为AE中点,又Q为AC中点,
所以PQ是△ACE的中位线,于是PQ∥CE.
∵CE 平面BCE,PQ 平面BCE,
∴PQ∥平面BCE.
(2)AD⊥平面ABEF BC⊥平面ABEF BC⊥AM.
在等腰梯形ABEF中,由AF=BE=2,EF=4,AB=2,
可得∠BEF=45°,BM=AM=2,
∴AB2=AM2+BM2,∴AM⊥BM.
又BC∩BM=B,∴AM⊥平面BCM.
(3)解法一:点F到平面BCE的距离是M到平面BCE的距离的2倍,
∵EM2=BE2+BM2,∴MB⊥BE,
∵MB⊥BC,BC∩BE=B,
∴MB⊥平面BCE,∴d=2MB=4.
解法二:VC-BEF=S△BEF·BC=BC,
VF-BCE=S△BCE·d=BC.
∵VC-BEF=VF-BCE,∴d=4.
21.(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)该五面体的体积为
。
(Ⅰ)取PC的中点为O,连FO,DO,可证
( http: / / www.21cnjy.com )FO∥ED,且FO=ED,所以四边形EFOD是平行四边形,从而可得EF∥DO,利用线面平行的判定,可得EF∥平面PDC;
(Ⅱ)先证明PD⊥平面ABCD,再证明BE⊥DP;
(Ⅲ)连接AC,由ABCD
( http: / / www.21cnjy.com )为平行四边形可知△ABC与△ADC面积相等,所以三棱锥P-ADC与三棱锥P-ABC体积相等,即五面体的体积为三棱锥P-ADC体积的二倍.
(Ⅰ)取PC的中点为O,连FO,DO,∵F,O分别为BP,PC的中点,
∴∥BC,且,又ABCD为平行四边形,∥BC,且,
∴∥ED,且
∴四边形EFOD是平行四边形
--------------------------------2分
即EF∥DO
又EF平面PDC
∴EF∥平面PDC.
----------------------
4分
(Ⅱ)若∠CDP=90°,则PD⊥DC,又AD⊥平面PDC
∴AD⊥DP,
∴PD⊥平面ABCD,
-------------
6分
∵BE平面ABCD,∴BE⊥DP
------------
8分
(Ⅲ)连结AC,由ABCD为平行四边形可知与面积相等,
所以三棱锥与三棱锥体积相等,
即五面体的体积为三棱锥体积的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4又∠CDP=120°PC=2,
由余弦定理并整理得,
解得DC=2
-------------------
10分
∴三棱锥的体积
∴该五面体的体积为
--------------------
12分
22.(1)证明见解析;(2)。
试题分析:(1),由勾股定理的逆定理可知;(2)以为坐标原点,分别为轴,轴的正方向,建立如图所示的空间直角坐标系,算出平面的法向量,而为平面的法向量,根据空间向量夹角余弦公式可得平面与平面所成角的余弦值。
试题解析:(1)由题设知,,,,连接,在中,,
所以,由勾股定理的逆定理可知。
(2)以为坐标原点,分别为轴,轴的正方向,建立如图所示的空间直角坐标系,根据题设可知,,所以,设平面的法向量为,则,即,令,可得,所以可取,另外为平面的法向量。所以,所以平面为平面所成角的余弦值为。
( http: / / www.21cnjy.com )
侧(左)视图
正(主)视图
俯视图
2
1
1
1
2
2
1
1
1
1
★祝考试顺利★
时间:120分钟
分值150分_
第I卷(选择题共60分)
一、选择题(本大题12小题,每小题5分,共60分)
1.一个几何体的三视图如图所示,则该几何体的体积的是(
)
(A)
(B)
(C)
(D)
2.
如图,一个不透明圆柱体的正视图和侧视图(
( http: / / www.21cnjy.com )左视图)为两全等的正方形,若将它竖直放在桌面上,则该圆柱体在桌面上从垂直位置旋转到水平位置的过程中,其在水平桌面上的正投影不可能是
(
)
3.设、是两条不同的直线,、是两个不同的平面.
考察下列命题,其中真命题是
A.
B.∥,∥
C.∥
D.
4.如图是正三棱锥V-ABC的正视图、侧视图和俯视图,则其侧视图的面积是(
)
( http: / / www.21cnjy.com )
A.4
B.5
C.6
D.7
5.(2015秋 石景山区期末)某建筑由相同的若干个房间组成,该楼的三视图如图所示,最高一层的房间在什么位置(
)
( http: / / www.21cnjy.com )
A.左前
B.右前
C.左后
D.右后
6.已知正方体的棱长为2,则其外接球的半径为
A. B. C. D.
7.在正四棱锥中,底面正方形的边长为1,侧棱长为2,则异面直线与所成角的大小为(
)
A.
B.
C.
D.
8.已知某几何体的三视图(单位:)如图所示,则该几何体的表面积是(
)
( http: / / www.21cnjy.com )
A.
B.
C.
D.
9.在空间中,下列命题错误的是(
)
A.一条直线与两个平行平面中的一个相交,则必与另一个相交
B.一个平面与两个平行平面相交,交线平行
C.平行于同一平面的两个平面平行
D.平行于同一直线的两个平面平行
10.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为(
)
A.1∶
B.
1∶9
C.
1∶
D.
1∶
11.在三棱锥中,侧面、侧面、侧两两互相垂直,且,设三棱锥的体积为,三棱锥的外接球的体积为,则(
)
A.
B.
C.
D.
12.在正方体中,、分别是、的中点,则异面直线与所成角的大小是(
)
A.
B.
C.
D.
第II卷(非选择题)
二
、填空题(本大题共4个小题,每题5分,满分20分)
13.某几何体的三视图如图所示(单位;cm),则该几何体的体积为
,表面积为
.
( http: / / www.21cnjy.com )
14.圆锥的底面半径为3,高为1,则圆锥的侧面积为
.
15.四面体ABCD四个面重心分别为E、F
( http: / / www.21cnjy.com )、G、H,则四面体EFGH表面积与四面体ABCD表面积的比值为
16.已知某棱锥的三视图如图所示,俯视图为正方形及一条对角线,根据图中所给的数据,该棱锥外接球的体积是_____.
( http: / / www.21cnjy.com )
三、解答题:本大题共6个小题,共70分。解答应写出文字说明、证明过程或演算步骤.
17.(本题10分)如图,在四棱锥中,
,底面是正方形,且.
( http: / / www.21cnjy.com )
(Ⅰ)若是中点,是的中点,求证:;
(Ⅱ)求四棱锥的侧面积.
18.(本题12分)如图,四棱锥中,
底面是直角梯形,
∥,,,侧面⊥底面,且是以为底的等腰三角形.
( http: / / www.21cnjy.com )
(1)证明:⊥;
(2)若三棱锥的体积等于,问:是否存
在过点的平面,分别交、于点,使得平面∥平面?若存在,求出的面积;若不存在,请说明理由.
19.(本题12分)在如图所示的四棱锥中,
四边形为正方形,
平面,且、、分别为、、的中点,.
( http: / / www.21cnjy.com )
(1)证明:平面;
(2)若,求二面角的余弦值.
20.(本题12分)如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4,AB=2,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
21.(本题12分)(本小题满分12分)如图所示多面体中,⊥平面,为平行四边形,分别为的中点,,,.
(1)求证:∥平面;
(2)若∠=90°,求证;
(3)若∠=120°,求该多面体的体积.
( http: / / www.21cnjy.com )
22.(本题12分)
如图1,已知矩形中,,分别是的中点,对角线与交于点,沿将矩形折起,使平面与平面所成角为60°,在图2中:
( http: / / www.21cnjy.com )
(1)求证:;
(2)求平面与平面所成角的余弦值。
答案
选择:1_5ABBCC
6_10
DDCDD
11_12
AD
填空:13.,.
14.
15.1:9
16.
17.(Ⅰ)证明见解析;(Ⅱ).
试题解析:(Ⅰ)证明:取的中点,连结.
( http: / / www.21cnjy.com )
因为是三角形的中位线,
所以.
又因为,所以.
所以四边形是平行四边形,所以,
又因为,,所以.
(Ⅱ)依题意得.
因为所以,
又因为,且,所以.
又因为,所以.
所以是直角三角形.
,所以.
同理可得.
所以四棱锥的侧面积是.
考点:直线与平面平行的判定定理;直线与平面垂直的判定定理;棱锥的侧面积。
18.(1)证明见解析;(2)存在,且面积为.
试题分析:(1)要证明线线垂直,可以通过线面垂直来证明,取中点,连,即证明平面.利用侧面⊥底面和在底面解三角形即可证明;(2)由三棱锥的体积,求出,取中点,中点,连得平面平面,取中点,.
试题解析:(1)取中点,连
∵为等腰三角形,
∴
在直角梯形中,由,,
得,
则为正三角形,∴
∴平面,⊥.
(2)由(1)知,又平面底面
∴平面
则,∴
取中点,中点,连
由
可知平面平面
取中点,∴
考点:空间立体几何证明平行与垂直.
19.(1)详见解析(2)
试题解析:(1)证明:连结分别交、于点、连结、为中点,
为中点,,
又为中点,
又为的中点,
平面平面平面.
( http: / / www.21cnjy.com )
(2)平面,又平面.如图,
以
为坐标原点,
所在直线分别为轴,轴,轴建立空间直角坐标系,
设,可知,则,平面,平面的一个法向量,设平面的法向量为,则,
即,令,则,,
由图可知,
二面角为钝角,
二面角的余弦值为.
( http: / / www.21cnjy.com )
`
20.(1)证明见解析;(2)证明见解析;(3).
试题分析:(1)因为分别是,的中点,由三角形的中位线性质知,∥,从而证明∥平面;(2)由题意易知,,又,所以,故,所以由线面垂直的判定定理可得结论;(3)可转化为到平面的距离的倍,再利用三棱锥的等体积法求到平面的距离.
试题解析:(1)因为AB∥EM,且AB=EM,所以四边形ABEM为平行四边形.
连接AE,则AE过点P,且P为AE中点,又Q为AC中点,
所以PQ是△ACE的中位线,于是PQ∥CE.
∵CE 平面BCE,PQ 平面BCE,
∴PQ∥平面BCE.
(2)AD⊥平面ABEF BC⊥平面ABEF BC⊥AM.
在等腰梯形ABEF中,由AF=BE=2,EF=4,AB=2,
可得∠BEF=45°,BM=AM=2,
∴AB2=AM2+BM2,∴AM⊥BM.
又BC∩BM=B,∴AM⊥平面BCM.
(3)解法一:点F到平面BCE的距离是M到平面BCE的距离的2倍,
∵EM2=BE2+BM2,∴MB⊥BE,
∵MB⊥BC,BC∩BE=B,
∴MB⊥平面BCE,∴d=2MB=4.
解法二:VC-BEF=S△BEF·BC=BC,
VF-BCE=S△BCE·d=BC.
∵VC-BEF=VF-BCE,∴d=4.
21.(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)该五面体的体积为
。
(Ⅰ)取PC的中点为O,连FO,DO,可证
( http: / / www.21cnjy.com )FO∥ED,且FO=ED,所以四边形EFOD是平行四边形,从而可得EF∥DO,利用线面平行的判定,可得EF∥平面PDC;
(Ⅱ)先证明PD⊥平面ABCD,再证明BE⊥DP;
(Ⅲ)连接AC,由ABCD
( http: / / www.21cnjy.com )为平行四边形可知△ABC与△ADC面积相等,所以三棱锥P-ADC与三棱锥P-ABC体积相等,即五面体的体积为三棱锥P-ADC体积的二倍.
(Ⅰ)取PC的中点为O,连FO,DO,∵F,O分别为BP,PC的中点,
∴∥BC,且,又ABCD为平行四边形,∥BC,且,
∴∥ED,且
∴四边形EFOD是平行四边形
--------------------------------2分
即EF∥DO
又EF平面PDC
∴EF∥平面PDC.
----------------------
4分
(Ⅱ)若∠CDP=90°,则PD⊥DC,又AD⊥平面PDC
∴AD⊥DP,
∴PD⊥平面ABCD,
-------------
6分
∵BE平面ABCD,∴BE⊥DP
------------
8分
(Ⅲ)连结AC,由ABCD为平行四边形可知与面积相等,
所以三棱锥与三棱锥体积相等,
即五面体的体积为三棱锥体积的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4又∠CDP=120°PC=2,
由余弦定理并整理得,
解得DC=2
-------------------
10分
∴三棱锥的体积
∴该五面体的体积为
--------------------
12分
22.(1)证明见解析;(2)。
试题分析:(1),由勾股定理的逆定理可知;(2)以为坐标原点,分别为轴,轴的正方向,建立如图所示的空间直角坐标系,算出平面的法向量,而为平面的法向量,根据空间向量夹角余弦公式可得平面与平面所成角的余弦值。
试题解析:(1)由题设知,,,,连接,在中,,
所以,由勾股定理的逆定理可知。
(2)以为坐标原点,分别为轴,轴的正方向,建立如图所示的空间直角坐标系,根据题设可知,,所以,设平面的法向量为,则,即,令,可得,所以可取,另外为平面的法向量。所以,所以平面为平面所成角的余弦值为。
( http: / / www.21cnjy.com )
侧(左)视图
正(主)视图
俯视图
2
1
1
1
2
2
1
1
1
1
同课章节目录
