20.1.1 平均数的意义及用计算器求平均数 同步练习
文档属性
| 名称 | 20.1.1 平均数的意义及用计算器求平均数 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 00:00:00 | ||
图片预览



文档简介
20.1.1 平均数的意义及用计算器求平均数
核心笔记: 1.算术平均数:一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为,即=(x1+x221世纪教育网版权所有
+…+xn).
2.平均数的意义:平均数表示一组数据的“平均水平”.
3.用计算器求算术平均数的步骤:①打开计算器;②启动统计计算功能;③输入所有数据;④计算出这组数据的算术平均数.
基础训练
1.小明记录了今年元月份某五天的最低温度(单位:℃):1,2,0,-1,-2,这五天的最低温度的平均值是( )21教育网
A.1 ℃ B.2 ℃
C.0 ℃ D.-1 ℃
2.我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
3.如图是小芹6月1日~7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
A.1小时
B.1.5小时
C.2小时
D.3小时
4.某校举行国庆文艺节目演出,由参加演出的10个班各派一名同学担任评委,下面是各评委给八(2)班一个节目的评分:【来源:21·世纪·教育·网】
评委编号
1
2
3
4
5
评分
7.25分
7.30分
7.05分
7.35分
10.00分
评委编号
6
7
8
9
10
评分
7.35分
7.30分
7.15分
6.00分
7.25分
(1)如果每个节目的得分取各个评委所给分的平均分,那么该节目的得分为____________分;?
(2)如果先去掉其中一个最高分和一个最低分,再取余下评委所给分的平均分,那么该节目的得分为____________分;?www.21-cn-jy.com
(3)两种得分相差____________分, ____________ (填序号(1)或(2))计算该节目的得分情况的方法比较合理.?21·世纪*教育网
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输成了15,则由此求出的平均数与实际平均数相差多少?
培优提升
1.期中考试后,学习小组组长算得该组5位同学数学成绩的平均分为M,如果把M当成另一位同学的分数,与原来的5个分数一起,算出这6个分数的平均值为N,那么M∶N的值为( )21*cnjy*com
A. B.1 C. D.2
2.某班50名同学的平均身高为168 cm,其中30名男生的平均身高为170 cm,则20名女生的平均身高是( )【出处:21教育名师】
A.165 cm B.168 cm C.169 cm D.167 cm
3.若数据2,3,7,-1,x的平均数为2,则x=______________;?
4.在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则甲同学以外的5名同学的平均分为_________ 分.?【版权所有:21教育】
5.现在有5个数,将各数都减去200,所得的差分别是8,6,-2,3,0,则原来5个数的平均数 =_________.?21教育名师原创作品
6.若a,b,c,d的平均数为m,则3a+1,3b+2,3c+3,3d+4的平均数是_________.?
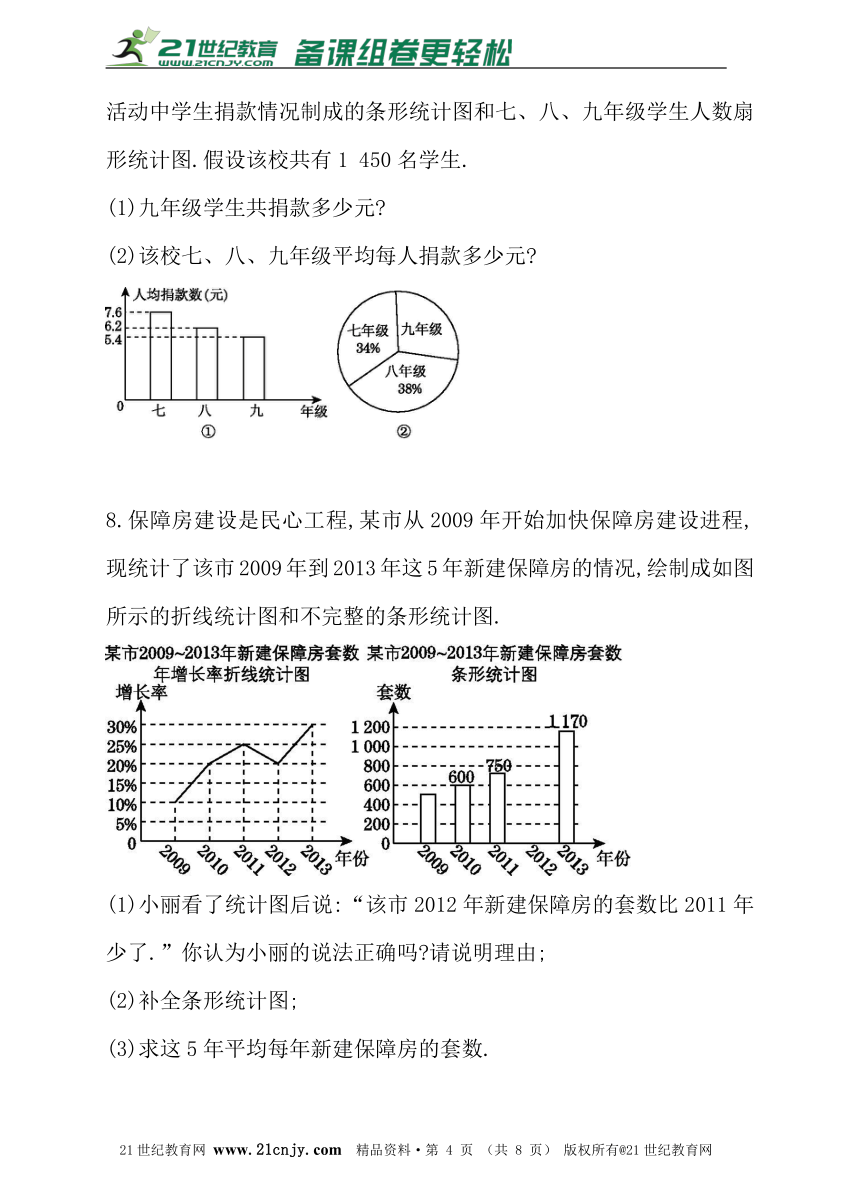
7.如图①②分别是根据某校七、八、九年级学生“献爱心”自愿捐款活动中学生捐款情况制成的条形统计图和七、八、九年级学生人数扇形统计图.假设该校共有1 450名学生.
(1)九年级学生共捐款多少元?
(2)该校七、八、九年级平均每人捐款多少元?
8.保障房建设是民心工程,某市从2009年开始加快保障房建设进程,现统计了该市2009年到2013年这5年新建保障房的情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2012年新建保障房的套数比2011年少了.”你认为小丽的说法正确吗?请说明理由;
(2)补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
9.个体户王某经营一家饭馆,下面是饭馆所有工作人员某个月的工资情况:王某10000元,厨师甲3800元,厨师乙3500元,杂工2200元,招待甲2800元,招待乙2500元,会计3200元.
(1)计算所有工作人员的平均工资;
(2)计算出的平均工资能否反映工作人员这个月收入的一般水平?
(3)去掉王某的工资后,再计算剩余工作人员的平均工资;
(4)(3)中的平均工资能代表一般工作人员的月收入吗?
(5)根据以上计算,从统计的观点看,你对(2)和(4)的结果有什么看法?
参考答案
【基础训练】
1.【答案】C
解:平均数等于所有数据的和除以数据的个数,应注意0也是一个数据.
2.【答案】C
解:=×(111+96+47+68+70+77+105)=82;故选C.
3.【答案】B
4.【答案】(1)7.4 (2)7.25 (3)0.15;(2)
解:(1)该节目的得分=(7.25+7.30+7.05+7.35+10.00+7.35+7.30+7.15+6.00+7.25)÷10=7.4(分);21·cn·jy·com
(2)该节目的得分=(7.25+7.30+7.05+7.35+7.35+7.30+7.15+7.25)÷8=7.25(分);
(3)7.4-7.25=0.15(分),(2)的方法较为合理,因为评委的评分常带有主观性,因此去掉一个最高分和一个最低分,能够使评分更具公平性.
5.解:该数据与实际数据相差105-15=90,∴求出的平均数与实际平均数相差=3.
【培优提升】
1.【答案】B
解:∵5位同学数学成绩的平均分为M,∴5位同学的总分为5M.把M当成另一位同学的分数,与原来的5位同学的分数加在一起,总分就为5M+M,∴这6个分数的平均值= (5M+M)=M=N,∴M∶N=1.故选B.
2.【答案】A 3.【答案】-1
4.【答案】71
解:包括甲同学在内的6名同学的总分为:74×6=444(分),甲同学以外的5名同学的总分为:444-89=355(分),则甲同学以外的5名同学的平均分为:=71(分).故填71.21cnjy.com
5.【答案】203
解:所得的差的平均数= ×(8+6-2+3+0)=3,所以原来5个数的平均数=3+200=203.故填203.【来源:21cnj*y.co*m】
6.【答案】3m+2.5
解:(3a+1)+(3b+2)+(3c+3)+(3d+4)=3(a+b+c+d)+10=3×4m+10=12m+10,所以平均数为(12m+10)÷4=3m+2.5.2-1-c-n-j-y
7.解:(1)九年级学生人数占的百分比为:1-34%-38%=28%,
九年级学生人数为:1450×28%=406(人),
所以九年级学生共捐款406×5.4=2192.4(元).
(2)七年级学生人数为:1450×34%=493(人),八年级学生人数为:1450×38%=551(人),所以七、八、九年级平均每人捐款21*cnjy*com
=6.452≈6.45(元).
8.解:(1)小丽的说法不正确.理由如下:该市2012年新建保障房的增长率比2011年的增长率减少了,
但是2012年新建保障房的套数比2011年增加了,故小丽的说法不正确.
(2)2012年新建保障房的套数为:750×(1+20%)=900(套),
2009年新建保障房的套数为:600÷(1+20%)=500(套),
补全条形统计图如图所示:
(3)这5年平均每年新建保障房的套数为:(500+600+750+900+1170)÷5=784(套).www-2-1-cnjy-com
9.解:(1)(10000+3800+3 500+2200+2800+2500+3200)÷7=4000(元),因此,所有工作人员的平均工资是4000元.
(2)不能反映工作人员这个月收入的一般水平.
(3)(3800+3500+2200+2800+2500+3200)÷6=3000(元),所以去掉王某的工资后,剩余工作人员的平均工资是3000元.2·1·c·n·j·y
(4)由于该平均工资接近一般工作人员的月工资收入,故能代表一般工作人员的月收入.
(5)从本题的计算中可以看出,个别特殊值对平均数具有很大的影响.
核心笔记: 1.算术平均数:一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为,即=(x1+x221世纪教育网版权所有
+…+xn).
2.平均数的意义:平均数表示一组数据的“平均水平”.
3.用计算器求算术平均数的步骤:①打开计算器;②启动统计计算功能;③输入所有数据;④计算出这组数据的算术平均数.
基础训练
1.小明记录了今年元月份某五天的最低温度(单位:℃):1,2,0,-1,-2,这五天的最低温度的平均值是( )21教育网
A.1 ℃ B.2 ℃
C.0 ℃ D.-1 ℃
2.我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
3.如图是小芹6月1日~7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
A.1小时
B.1.5小时
C.2小时
D.3小时
4.某校举行国庆文艺节目演出,由参加演出的10个班各派一名同学担任评委,下面是各评委给八(2)班一个节目的评分:【来源:21·世纪·教育·网】
评委编号
1
2
3
4
5
评分
7.25分
7.30分
7.05分
7.35分
10.00分
评委编号
6
7
8
9
10
评分
7.35分
7.30分
7.15分
6.00分
7.25分
(1)如果每个节目的得分取各个评委所给分的平均分,那么该节目的得分为____________分;?
(2)如果先去掉其中一个最高分和一个最低分,再取余下评委所给分的平均分,那么该节目的得分为____________分;?www.21-cn-jy.com
(3)两种得分相差____________分, ____________ (填序号(1)或(2))计算该节目的得分情况的方法比较合理.?21·世纪*教育网
5.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输成了15,则由此求出的平均数与实际平均数相差多少?
培优提升
1.期中考试后,学习小组组长算得该组5位同学数学成绩的平均分为M,如果把M当成另一位同学的分数,与原来的5个分数一起,算出这6个分数的平均值为N,那么M∶N的值为( )21*cnjy*com
A. B.1 C. D.2
2.某班50名同学的平均身高为168 cm,其中30名男生的平均身高为170 cm,则20名女生的平均身高是( )【出处:21教育名师】
A.165 cm B.168 cm C.169 cm D.167 cm
3.若数据2,3,7,-1,x的平均数为2,则x=______________;?
4.在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则甲同学以外的5名同学的平均分为_________ 分.?【版权所有:21教育】
5.现在有5个数,将各数都减去200,所得的差分别是8,6,-2,3,0,则原来5个数的平均数 =_________.?21教育名师原创作品
6.若a,b,c,d的平均数为m,则3a+1,3b+2,3c+3,3d+4的平均数是_________.?
7.如图①②分别是根据某校七、八、九年级学生“献爱心”自愿捐款活动中学生捐款情况制成的条形统计图和七、八、九年级学生人数扇形统计图.假设该校共有1 450名学生.
(1)九年级学生共捐款多少元?
(2)该校七、八、九年级平均每人捐款多少元?
8.保障房建设是民心工程,某市从2009年开始加快保障房建设进程,现统计了该市2009年到2013年这5年新建保障房的情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2012年新建保障房的套数比2011年少了.”你认为小丽的说法正确吗?请说明理由;
(2)补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
9.个体户王某经营一家饭馆,下面是饭馆所有工作人员某个月的工资情况:王某10000元,厨师甲3800元,厨师乙3500元,杂工2200元,招待甲2800元,招待乙2500元,会计3200元.
(1)计算所有工作人员的平均工资;
(2)计算出的平均工资能否反映工作人员这个月收入的一般水平?
(3)去掉王某的工资后,再计算剩余工作人员的平均工资;
(4)(3)中的平均工资能代表一般工作人员的月收入吗?
(5)根据以上计算,从统计的观点看,你对(2)和(4)的结果有什么看法?
参考答案
【基础训练】
1.【答案】C
解:平均数等于所有数据的和除以数据的个数,应注意0也是一个数据.
2.【答案】C
解:=×(111+96+47+68+70+77+105)=82;故选C.
3.【答案】B
4.【答案】(1)7.4 (2)7.25 (3)0.15;(2)
解:(1)该节目的得分=(7.25+7.30+7.05+7.35+10.00+7.35+7.30+7.15+6.00+7.25)÷10=7.4(分);21·cn·jy·com
(2)该节目的得分=(7.25+7.30+7.05+7.35+7.35+7.30+7.15+7.25)÷8=7.25(分);
(3)7.4-7.25=0.15(分),(2)的方法较为合理,因为评委的评分常带有主观性,因此去掉一个最高分和一个最低分,能够使评分更具公平性.
5.解:该数据与实际数据相差105-15=90,∴求出的平均数与实际平均数相差=3.
【培优提升】
1.【答案】B
解:∵5位同学数学成绩的平均分为M,∴5位同学的总分为5M.把M当成另一位同学的分数,与原来的5位同学的分数加在一起,总分就为5M+M,∴这6个分数的平均值= (5M+M)=M=N,∴M∶N=1.故选B.
2.【答案】A 3.【答案】-1
4.【答案】71
解:包括甲同学在内的6名同学的总分为:74×6=444(分),甲同学以外的5名同学的总分为:444-89=355(分),则甲同学以外的5名同学的平均分为:=71(分).故填71.21cnjy.com
5.【答案】203
解:所得的差的平均数= ×(8+6-2+3+0)=3,所以原来5个数的平均数=3+200=203.故填203.【来源:21cnj*y.co*m】
6.【答案】3m+2.5
解:(3a+1)+(3b+2)+(3c+3)+(3d+4)=3(a+b+c+d)+10=3×4m+10=12m+10,所以平均数为(12m+10)÷4=3m+2.5.2-1-c-n-j-y
7.解:(1)九年级学生人数占的百分比为:1-34%-38%=28%,
九年级学生人数为:1450×28%=406(人),
所以九年级学生共捐款406×5.4=2192.4(元).
(2)七年级学生人数为:1450×34%=493(人),八年级学生人数为:1450×38%=551(人),所以七、八、九年级平均每人捐款21*cnjy*com
=6.452≈6.45(元).
8.解:(1)小丽的说法不正确.理由如下:该市2012年新建保障房的增长率比2011年的增长率减少了,
但是2012年新建保障房的套数比2011年增加了,故小丽的说法不正确.
(2)2012年新建保障房的套数为:750×(1+20%)=900(套),
2009年新建保障房的套数为:600÷(1+20%)=500(套),
补全条形统计图如图所示:
(3)这5年平均每年新建保障房的套数为:(500+600+750+900+1170)÷5=784(套).www-2-1-cnjy-com
9.解:(1)(10000+3800+3 500+2200+2800+2500+3200)÷7=4000(元),因此,所有工作人员的平均工资是4000元.
(2)不能反映工作人员这个月收入的一般水平.
(3)(3800+3500+2200+2800+2500+3200)÷6=3000(元),所以去掉王某的工资后,剩余工作人员的平均工资是3000元.2·1·c·n·j·y
(4)由于该平均工资接近一般工作人员的月工资收入,故能代表一般工作人员的月收入.
(5)从本题的计算中可以看出,个别特殊值对平均数具有很大的影响.
