28.2.1 解直角三角形 同步练习
图片预览



文档简介
28.2.1 解直角三角形
基础训练
知识点1 已知两边解三角形
1.在Rt△ABC中,∠C=90°.
(1)若c=6,a=6,则b=_________,∠B=_______,∠A=_______;?
(2)若a=4,b=4,则∠A=_______,∠B=_______,c=_______.?
2.如图,△ABC中,∠B=90°,BC=2AB,则cos A=( )
A. B. C. D.
3.如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tan B=( )21·cn·jy·com
A.2 B.2 C. D.
知识点2 已知一边及一锐角解三角形
4.在Rt△ABC中,∠C=90°.
(1)若∠B=60°,BC=,则
∠A=__________,AC=_________,AB=_________;?
(2)若∠A=45°,AB=2,则
∠B=_________,AC=_________,BC=_________.?
5.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC等于( )
A.3sin 40° B.3sin 50°
C.3tan 40° D.3tan 50°
6.如图,△ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP长不可能是( )www.21-cn-jy.com
A.3.5 B.4.2 C.5.8 D.7
7.如图,在Rt△ABC中,∠C=90°, D为BC上一
点,∠DAC=30°,BD=2,AB=2,则AC的长是( )
A. B.2 C.3 D.
知识点3 已知一边及一锐角的三角函数值解三角形
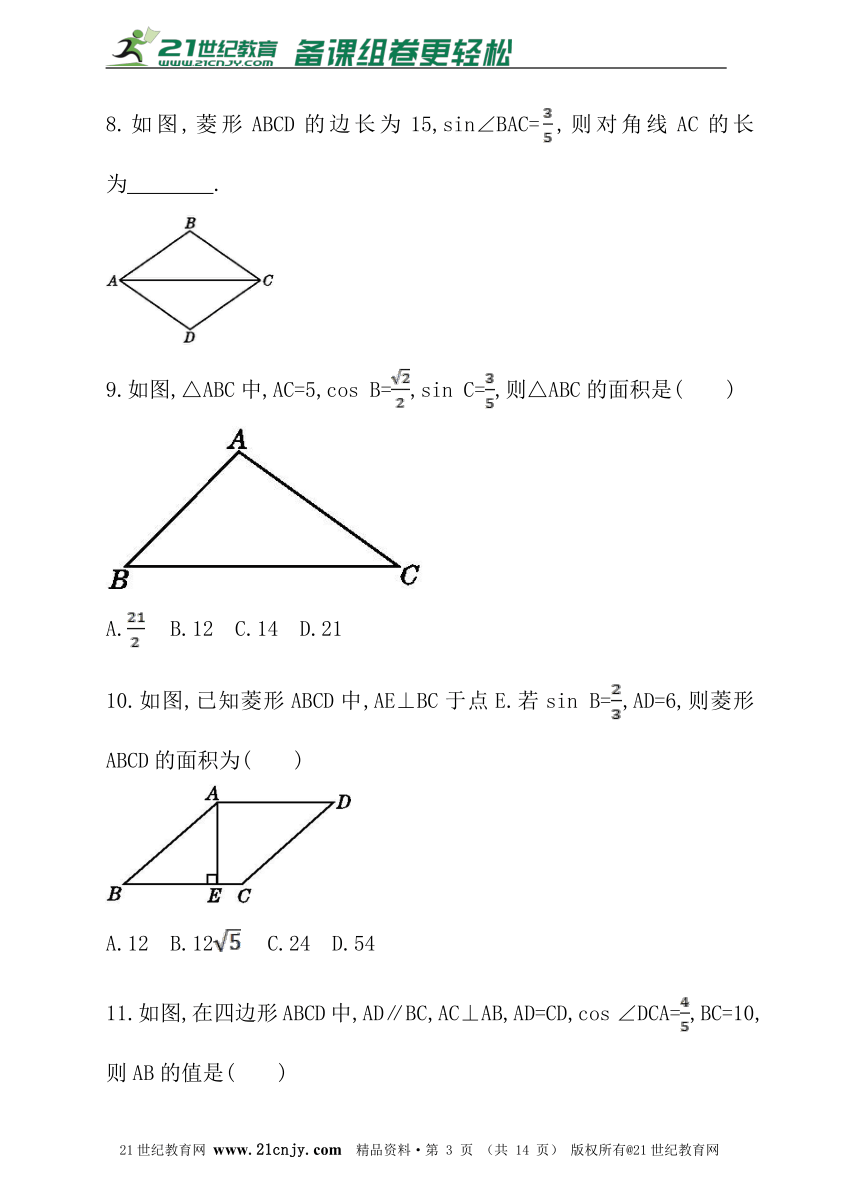
8.如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为 .?
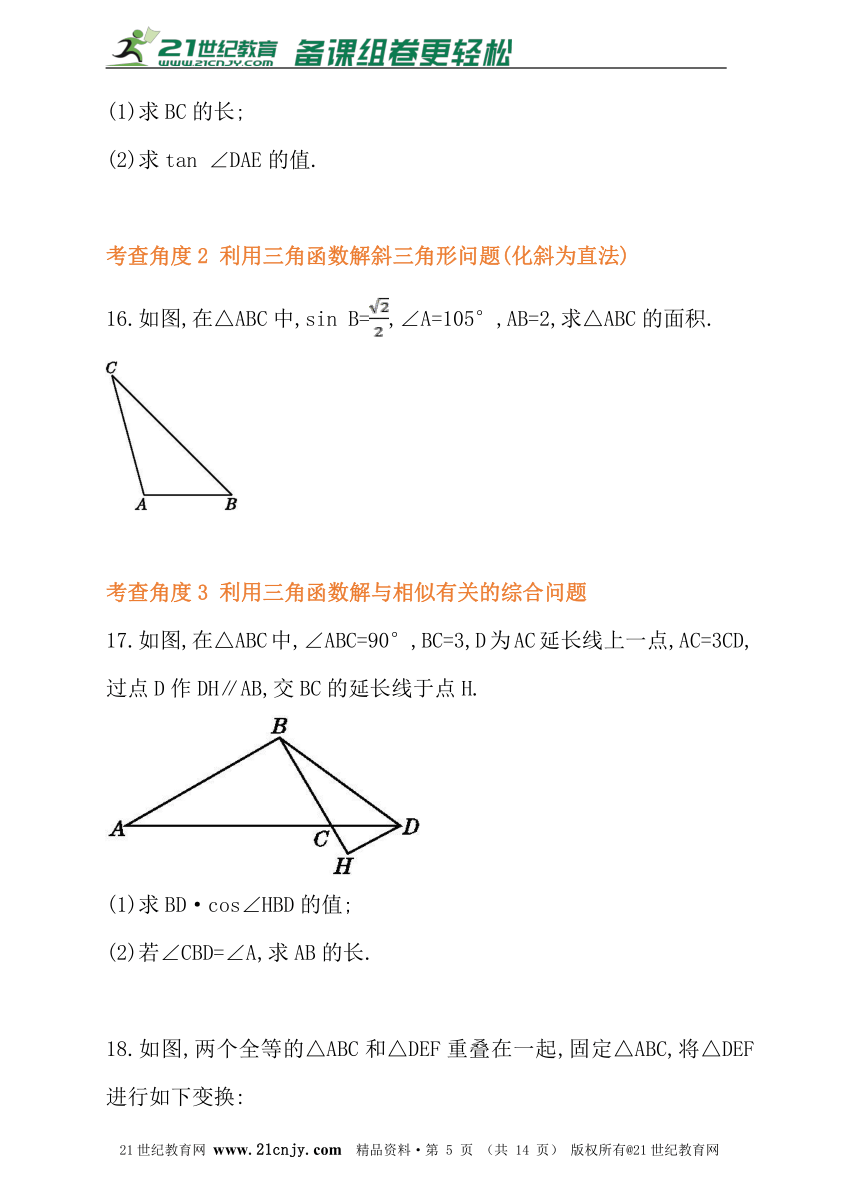
9.如图,△ABC中,AC=5,cos B=,sin C=,则△ABC的面积是( )
A. B.12 C.14 D.21
10.如图,已知菱形ABCD中,AE⊥BC于点E.若sin B=,AD=6,则菱形ABCD的面积为( )21·世纪*教育网
A.12 B.12 C.24 D.54
11.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos ∠DCA=,BC=10,则AB的值是( )21世纪教育网版权所有
A.3 B.6 C.8 D.9
12.在△ABC中,AB=2,AC=,∠B=30°.求∠BAC的度数.
提升训练
考查角度1 利用三角函数解直角三角形
13.如图,在Rt△ABC中,∠C=90°,AC=BC=3,解这个直角三角形.
14.在Rt△ABC中,∠C=90°,已知b=10,∠B=60°,解这个直角三角形.
15.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=,AD=1.www-2-1-cnjy-com
(1)求BC的长;
(2)求tan ∠DAE的值.
考查角度2 利用三角函数解斜三角形问题(化斜为直法)
16.如图,在△ABC中,sin B=,∠A=105°,AB=2,求△ABC的面积.
考查角度3 利用三角函数解与相似有关的综合问题
17.如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.2-1-c-n-j-y
(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
18.如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图①,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF,AD,BD,请直接写出S△ABC与S四边形AFBD的关系.21教育网
(2)如图②,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明.21*cnjy*com
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,并求出sin∠CGF的值.21*cnjy*com
①
②
19.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.
(1)求证:PA是☉O的切线.
(2)若=,且OC=4,求PA的长和tan D的值.
参考答案
1.【答案】(1)6;45°;45° (2)60°;30°;8
2.【答案】D 3.【答案】B
4.【答案】(1)30°;;2 (2)45°;;
5.【答案】D 6.【答案】D 7.【答案】A
8.【答案】24
9.【答案】A
解:如图,过点A作AD⊥BC.因为cos B=,所以∠B=45°,所以AD=BD.因为sin C==,所以=,所以AD=BD=3,所以2·1·c·n·j·y
DC===4,所以BC=BD+DC=7,所以S△ABC=BC·AD=×7×3=.
10.【答案】C
解:∵四边形ABCD是菱形,AD=6,∴AB=BC=6.在Rt△ABE中,sin B=,∵sin B=,21cnjy.com
∴=,解得AE=4.∴菱形ABCD的面积是6×4=24.故选C.
11.【答案】B
解:∵AD∥BC,∴∠DAC=∠ACB.
∵AD=CD,
∴∠DAC=∠DCA.∴∠ACB=∠DCA.
∴cos∠ACB=cos∠DCA=,即==,
∴AC=8,∴AB==6.
12.解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D.在Rt△ABD中,∵∠B=30°,【来源:21·世纪·教育·网】
∴∠BAD=60°,AD=AB·sin 30°=1.
在Rt△ACD中,CD===1,
∴△ACD是等腰直角三角形,则∠CAD=45°,
∴∠BAC=∠BAD+∠CAD=60°+45°=105°.
(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D.
∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°.
∴CD===1,
∴∠DAC=45°,
∴∠BAC=∠BAD-∠DAC=60°-45°=15°.
综上可知,∠BAC的度数为105°或15°.
常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解.
13.解:在Rt△ABC中,AB===6.
∵tan A===1,∴∠A=45°.
∴∠B=90°-∠A=90°-45°=45°.
14.解:∵∠B=60°,∴∠A=90°-∠B=30°.
∵tan B=,
∴a====.
∵sin B=,
∴c====.
方法解:已知一个锐角时,可以先根据直角三角形的两锐角互余来计算另一个锐角的度数.已知一个锐角及对边,常通过正切和正弦来解直角三角形.【来源:21cnj*y.co*m】
15.解:(1)在△ABC中,∵AD是BC边上的高,∴∠ADB=∠ADC=90°.在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1.在△ADB中,∵∠ADB=90°,sin B=,AD=1,∴AB==3,∴BD==2,∴BC=BD+DC=2+1.【出处:21教育名师】
(2)∵AE是BC边上的中线,∴CE=BC=+,∴DE=CE-CD=-,∴tan ∠DAE==-.【版权所有:21教育】
16.解:过A作AD⊥BC于D.
在Rt△ABD中,易得∠B=45°,又AB=2,∴∠DAB=∠B=45°,AD=BD=2×=,∴∠CAD=105°-45°=60°.21教育名师原创作品
在Rt△CAD中,tan∠CAD=,
∴CD=AD·tan∠CAD=×tan 60°=.
∴BC=CD+BD=+.
∴S△ABC=·BC·AD=(+)×=+1.
17.解:(1)∵DH∥AB,∴∠BHD=∠ABC=90°,
∴△ABC∽△DHC,∴=.
∵AC=3CD,BC=3,∴CH=1.∴BH=BC+CH=4.
在Rt△BHD中,cos ∠HBD=.
∴BD·cos∠HBD=BH=4.
(2)方法一:
∵∠A=∠CBD,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴=.
∵△ABC∽△DHC,
∴==,∴AB=3DH,
∴=,DH=2,∴AB=6.
方法二:
∵∠CBD=∠A,∠BDC=∠ADB,
∴△CDB∽△BDA,
∴=,BD2=CD·AD.∴BD2=CD·4CD=4CD2.
∴BD=2CD.
∵△CDB∽△BDA,∴=.∴=.
∴AB=6.
18.解:(1)S△ABC=S四边形AFBD.
(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°.
理由如下:
∵F为BC的中点,
∴CF=BF.
∵CF=AD,
∴AD=BF.
又∵AD∥BF,
∴四边形AFBD为平行四边形.
∵AB=AC,F为BC的中点,
∴AF⊥BC.
∴平行四边形AFBD为矩形.
∵∠BAC=90°,F为BC的中点,
∴AF=BC=BF.
∴四边形AFBD为正方形.
(3)正确画出图形如图.
由(2)知,△ABC为等腰直角三角形,AF⊥BC,
设CF=k,则GF=EF=CB=2k.
由勾股定理,得:CG=k.
sin ∠CGF===.
19.(1)证明:如图,连接BO,∵PB为☉O的切线,B为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.又∵OP=OP,
∴△PAO≌△PBO,
∴∠PAO=∠PBO=90°,PA=PB,
∴PA是☉O的切线.
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,
∴==.又∵OC=4,∴AC=6.
在Rt△AOC中,
OA===2,
∴PA=OA=3,∴PB=3.
在Rt△PAO中,PO===13.
如图,连接BE.∵AE为直径,∴∠ABE=90°.又∵OC⊥AB,
∴BE∥OP,∴△DBE∽△DPO,BE=2OC=8.
∴=.
即=.解得BD=.
∴在Rt△DBO中,tan D===.
基础训练
知识点1 已知两边解三角形
1.在Rt△ABC中,∠C=90°.
(1)若c=6,a=6,则b=_________,∠B=_______,∠A=_______;?
(2)若a=4,b=4,则∠A=_______,∠B=_______,c=_______.?
2.如图,△ABC中,∠B=90°,BC=2AB,则cos A=( )
A. B. C. D.
3.如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tan B=( )21·cn·jy·com
A.2 B.2 C. D.
知识点2 已知一边及一锐角解三角形
4.在Rt△ABC中,∠C=90°.
(1)若∠B=60°,BC=,则
∠A=__________,AC=_________,AB=_________;?
(2)若∠A=45°,AB=2,则
∠B=_________,AC=_________,BC=_________.?
5.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC等于( )
A.3sin 40° B.3sin 50°
C.3tan 40° D.3tan 50°
6.如图,△ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP长不可能是( )www.21-cn-jy.com
A.3.5 B.4.2 C.5.8 D.7
7.如图,在Rt△ABC中,∠C=90°, D为BC上一
点,∠DAC=30°,BD=2,AB=2,则AC的长是( )
A. B.2 C.3 D.
知识点3 已知一边及一锐角的三角函数值解三角形
8.如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为 .?
9.如图,△ABC中,AC=5,cos B=,sin C=,则△ABC的面积是( )
A. B.12 C.14 D.21
10.如图,已知菱形ABCD中,AE⊥BC于点E.若sin B=,AD=6,则菱形ABCD的面积为( )21·世纪*教育网
A.12 B.12 C.24 D.54
11.如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos ∠DCA=,BC=10,则AB的值是( )21世纪教育网版权所有
A.3 B.6 C.8 D.9
12.在△ABC中,AB=2,AC=,∠B=30°.求∠BAC的度数.
提升训练
考查角度1 利用三角函数解直角三角形
13.如图,在Rt△ABC中,∠C=90°,AC=BC=3,解这个直角三角形.
14.在Rt△ABC中,∠C=90°,已知b=10,∠B=60°,解这个直角三角形.
15.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=,AD=1.www-2-1-cnjy-com
(1)求BC的长;
(2)求tan ∠DAE的值.
考查角度2 利用三角函数解斜三角形问题(化斜为直法)
16.如图,在△ABC中,sin B=,∠A=105°,AB=2,求△ABC的面积.
考查角度3 利用三角函数解与相似有关的综合问题
17.如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.2-1-c-n-j-y
(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
18.如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图①,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF,AD,BD,请直接写出S△ABC与S四边形AFBD的关系.21教育网
(2)如图②,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明.21*cnjy*com
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,并求出sin∠CGF的值.21*cnjy*com
①
②
19.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.
(1)求证:PA是☉O的切线.
(2)若=,且OC=4,求PA的长和tan D的值.
参考答案
1.【答案】(1)6;45°;45° (2)60°;30°;8
2.【答案】D 3.【答案】B
4.【答案】(1)30°;;2 (2)45°;;
5.【答案】D 6.【答案】D 7.【答案】A
8.【答案】24
9.【答案】A
解:如图,过点A作AD⊥BC.因为cos B=,所以∠B=45°,所以AD=BD.因为sin C==,所以=,所以AD=BD=3,所以2·1·c·n·j·y
DC===4,所以BC=BD+DC=7,所以S△ABC=BC·AD=×7×3=.
10.【答案】C
解:∵四边形ABCD是菱形,AD=6,∴AB=BC=6.在Rt△ABE中,sin B=,∵sin B=,21cnjy.com
∴=,解得AE=4.∴菱形ABCD的面积是6×4=24.故选C.
11.【答案】B
解:∵AD∥BC,∴∠DAC=∠ACB.
∵AD=CD,
∴∠DAC=∠DCA.∴∠ACB=∠DCA.
∴cos∠ACB=cos∠DCA=,即==,
∴AC=8,∴AB==6.
12.解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D.在Rt△ABD中,∵∠B=30°,【来源:21·世纪·教育·网】
∴∠BAD=60°,AD=AB·sin 30°=1.
在Rt△ACD中,CD===1,
∴△ACD是等腰直角三角形,则∠CAD=45°,
∴∠BAC=∠BAD+∠CAD=60°+45°=105°.
(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D.
∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°.
∴CD===1,
∴∠DAC=45°,
∴∠BAC=∠BAD-∠DAC=60°-45°=15°.
综上可知,∠BAC的度数为105°或15°.
常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解.
13.解:在Rt△ABC中,AB===6.
∵tan A===1,∴∠A=45°.
∴∠B=90°-∠A=90°-45°=45°.
14.解:∵∠B=60°,∴∠A=90°-∠B=30°.
∵tan B=,
∴a====.
∵sin B=,
∴c====.
方法解:已知一个锐角时,可以先根据直角三角形的两锐角互余来计算另一个锐角的度数.已知一个锐角及对边,常通过正切和正弦来解直角三角形.【来源:21cnj*y.co*m】
15.解:(1)在△ABC中,∵AD是BC边上的高,∴∠ADB=∠ADC=90°.在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1.在△ADB中,∵∠ADB=90°,sin B=,AD=1,∴AB==3,∴BD==2,∴BC=BD+DC=2+1.【出处:21教育名师】
(2)∵AE是BC边上的中线,∴CE=BC=+,∴DE=CE-CD=-,∴tan ∠DAE==-.【版权所有:21教育】
16.解:过A作AD⊥BC于D.
在Rt△ABD中,易得∠B=45°,又AB=2,∴∠DAB=∠B=45°,AD=BD=2×=,∴∠CAD=105°-45°=60°.21教育名师原创作品
在Rt△CAD中,tan∠CAD=,
∴CD=AD·tan∠CAD=×tan 60°=.
∴BC=CD+BD=+.
∴S△ABC=·BC·AD=(+)×=+1.
17.解:(1)∵DH∥AB,∴∠BHD=∠ABC=90°,
∴△ABC∽△DHC,∴=.
∵AC=3CD,BC=3,∴CH=1.∴BH=BC+CH=4.
在Rt△BHD中,cos ∠HBD=.
∴BD·cos∠HBD=BH=4.
(2)方法一:
∵∠A=∠CBD,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴=.
∵△ABC∽△DHC,
∴==,∴AB=3DH,
∴=,DH=2,∴AB=6.
方法二:
∵∠CBD=∠A,∠BDC=∠ADB,
∴△CDB∽△BDA,
∴=,BD2=CD·AD.∴BD2=CD·4CD=4CD2.
∴BD=2CD.
∵△CDB∽△BDA,∴=.∴=.
∴AB=6.
18.解:(1)S△ABC=S四边形AFBD.
(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°.
理由如下:
∵F为BC的中点,
∴CF=BF.
∵CF=AD,
∴AD=BF.
又∵AD∥BF,
∴四边形AFBD为平行四边形.
∵AB=AC,F为BC的中点,
∴AF⊥BC.
∴平行四边形AFBD为矩形.
∵∠BAC=90°,F为BC的中点,
∴AF=BC=BF.
∴四边形AFBD为正方形.
(3)正确画出图形如图.
由(2)知,△ABC为等腰直角三角形,AF⊥BC,
设CF=k,则GF=EF=CB=2k.
由勾股定理,得:CG=k.
sin ∠CGF===.
19.(1)证明:如图,连接BO,∵PB为☉O的切线,B为切点,
∴OB⊥PD,∠PBO=90°.
又∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC.又∵OP=OP,
∴△PAO≌△PBO,
∴∠PAO=∠PBO=90°,PA=PB,
∴PA是☉O的切线.
(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,
∴△AOC∽△POA,
∴==.又∵OC=4,∴AC=6.
在Rt△AOC中,
OA===2,
∴PA=OA=3,∴PB=3.
在Rt△PAO中,PO===13.
如图,连接BE.∵AE为直径,∴∠ABE=90°.又∵OC⊥AB,
∴BE∥OP,∴△DBE∽△DPO,BE=2OC=8.
∴=.
即=.解得BD=.
∴在Rt△DBO中,tan D===.
