28.2.2 解直角三角形的一般应用 同步练习
文档属性
| 名称 | 28.2.2 解直角三角形的一般应用 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 22:26:57 | ||
图片预览



文档简介
28.2.2 解直角三角形的一般应用
基础训练
知识点1 利用解直角三角形解一般三角形应用问题
1.为解决停车难的问题,在如图所示的一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出___________个这样的停车位.
2.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,在D点测得∠ADB=60°,又CD=60 m,则河宽AB为___________m.(结果保留根号)?2·1·c·n·j·y
3.如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长是 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)21·世纪*教育网
4.长为4m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了 m.【来源:21cnj*y.co*m】
5.如图,是意大利著名的比萨斜塔,塔身的中心线与垂直中心线的夹角A约为5°28',塔身AB的长为54.5 m,则塔顶中心偏离垂直中心线的距离BC是( )【出处:21教育名师】
A.54.5×sin 5°28'm B.54.5×cos 5°28'm
C.54.5×tan 5°28'm D. m
6.如图,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )www-2-1-cnjy-com
A.asin 40°米 B.acos 40°米
C.atan 40°米 D.米
知识点2 利用解直角三角形解与圆相关的问题
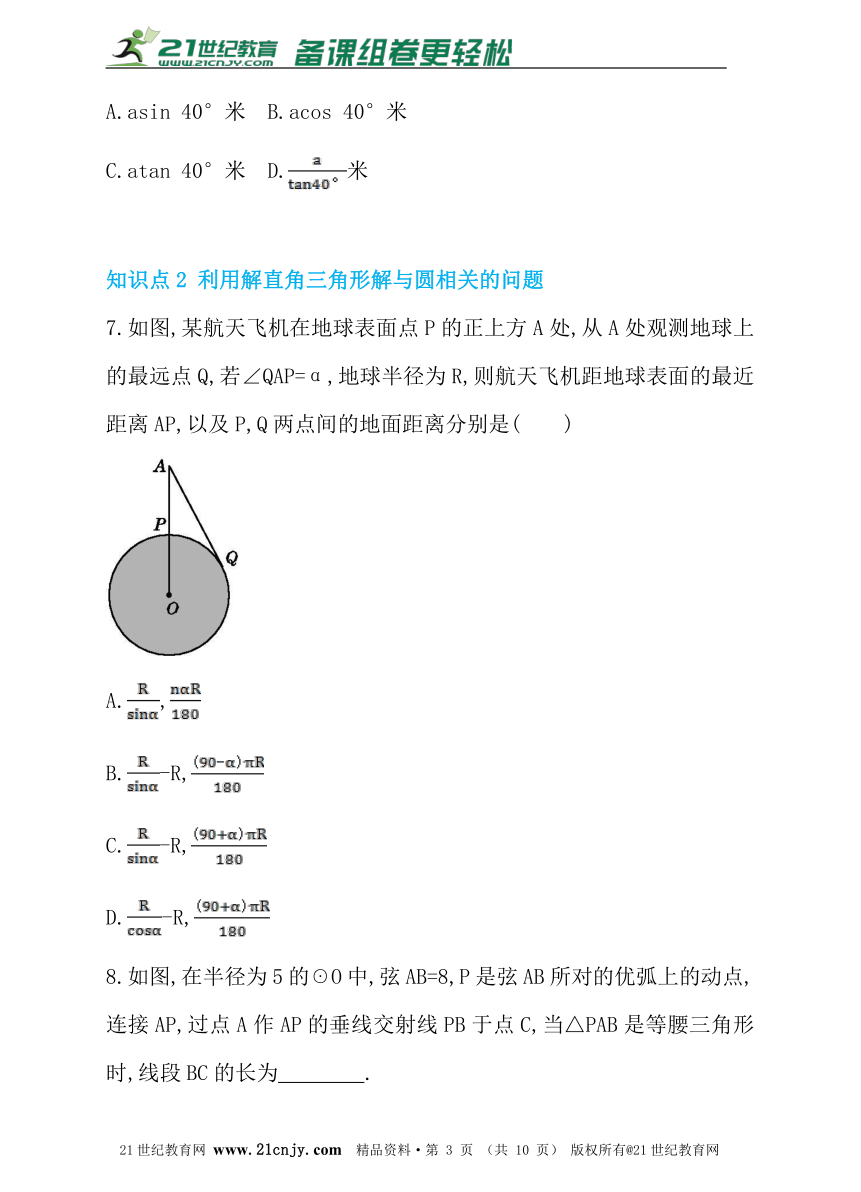
7.如图,某航天飞机在地球表面点P的正上方A处,从A处观测地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P,Q两点间的地面距离分别是( )2-1-c-n-j-y
A.,
B.-R,
C.-R,
D.-R,
8.如图,在半径为5的☉O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为 .21世纪教育网版权所有
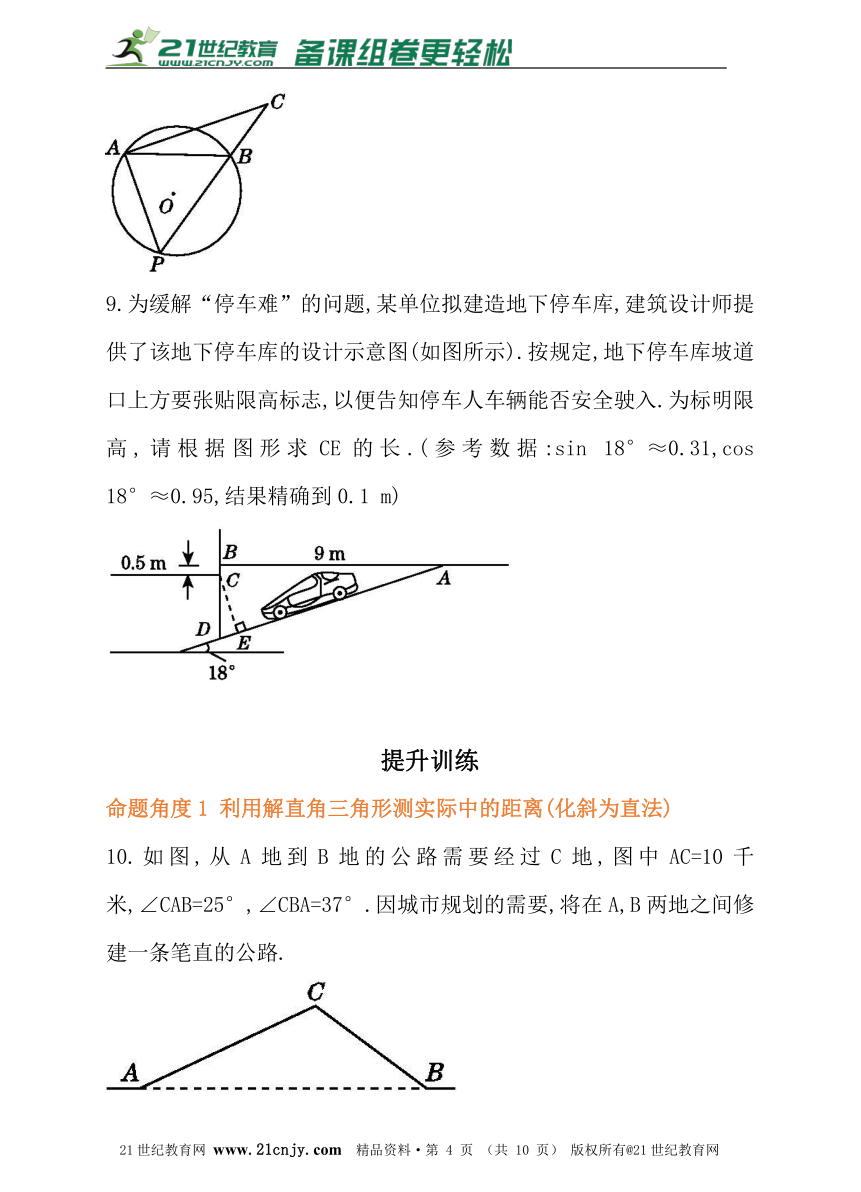
9.为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图(如图所示).按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.为标明限高,请根据图形求CE的长.(参考数据:sin 18°≈0.31,cos 18°≈0.95,结果精确到0.1 m)21*cnjy*com
提升训练
命题角度1 利用解直角三角形测实际中的距离(化斜为直法)
10.如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.www.21-cn-jy.com
(1)求改直后的公路AB的长;
(2)问:公路改直后比原来缩短了多少千米?(sin 25°≈0.42,cos 25°≈0.91,sin 37°≈0.60,tan 37°≈0.75)21·cn·jy·com
命题角度2 利用解直角三角形测下降高度
11.如图,这是一把可调节座椅的侧面示意图,已知头枕上的点到调节器点O处的距离为80 cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA'处,求调整后点A'比调整前点A的高度降低了多少厘米?(结果取整数)【来源:21·世纪·教育·网】
(参考数据:sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70)
探究培优
拔尖角度 利用解直角三角形解方案设计问题
12.如图所示,A,B为两个村庄,AB,BC,CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从点E处开始铺设通往村庄A、村庄B的一条电线,共有如下两种铺设方案:21cnjy.com
方案一:E→D→A→B;方案二:E→C→B→A.
经测量得AB=4 km,BC=10 km,CE=6 km,∠BDC=45°,∠ABD=15°.已
知地上电缆的修建费为2万元/km,水下电缆的修建费为4万元/km.
(1)求出河宽AD.(结果保留根号)
(2)求出公路CD的长.
(3)哪种方案铺设电缆的费用较低?请说明理由.
参考答案
1.【答案】17 2.【答案】30 3.【答案】
4.【答案】2(-)
5.【答案】A 6.【答案】C 7.【答案】B
8.【答案】8或或
解:(1)当AB=AP时,如图①,作OH⊥AB于点H,延长AO交PB于点G;
易知=cos∠APC=cos∠AOH==?PC=AP=.
又知PG===?BC=PC-2PG=-=.
(2)当PA=PB时,如图②,延长PO交AB于点K,易知
OK=3,PK=8,PB=PA=4,
易知=cos ∠APC=cos∠AOK==?PC=AP=?BC=PC-PB=
(3)当BA=BP时,如图③,由∠C=90°-∠P=90°-∠PAB=∠CAB?BC=AB=8.
综上:BC=8或或.
9.解:在Rt△ABD中,AB=9 m,∠BAE=18°,
∴BD=AB·tan ∠BAE=9tan 18°(m).
∴CD=BD-BC=(9tan 18°-0.5)m.
∵∠CDE=90°-∠BAE=90°-∠DCE,
∴∠DCE=∠BAE=18°.
在Rt△CDE中,有cos ∠DCE=,
∴CE=CD·cos 18°=(9tan 18°-0.5)×cos 18°
=9××cos 18°-0.5cos 18°
=9sin 18°-0.5cos 18°
≈9×0.31-0.5×0.95
=2.315≈2.3(m).
分析:解此类题的关键是构造数学模型,将求限高的问题转化为解直角三角形的问题.此外,为了安全,此处宜用去尾法取近似值.
10.解:(1)作CH⊥AB于点H,在Rt△ACH中,CH=AC·sin ∠CAB=AC·sin 25°≈10×0.42=4.2(千米),21教育网
AH=AC·cos ∠CAB=AC·cos 25°≈10×0.91=9.1(千米).
在Rt△BCH中,BH=≈=5.6(千米).
∴AB=AH+BH≈9.1+5.6=14.7(千米).
(2)BC=≈=7.0(千米),
∴AC+BC-AB≈10+7.0-14.7=2.3(千米).
∴公路改直后比原来缩短了约2.3千米.
11.解:过点A'作A'H⊥OA于点H,
由旋转可知,OA'=OA=80 cm,
在Rt△OA'H中,OH=OA'cos 35°≈80×0.82=65.6(cm).
∴AH=OA-OH≈80-65.6=14.4≈14(cm).
答:调整后点A'比调整前点A的高度降低了14 cm.
12.解:(1)如图,过点B作BF⊥AD,交DA的延长线于点F.
∵CD⊥AD,∠BDC=45°,∴∠BDF=45°.
在Rt△BFA中,∠BAF=∠ABD+∠BDF=15°+45°=60°,
∴BF=AB·sin 60°=4×=6(km),AF=AB·cos 60°=4×
=2(km).
在Rt△BFD中,∵∠BDF=45°,∴DF=BF=6 km.
∴AD=DF-AF=(6-2)km.即河宽AD为(6-2)km.
(2)如图,过点B作BG⊥CD于点G,易证四边形BFDG是正方形,∴BG=GD=BF=6 km.
在Rt△BGC中,CG===8(km),
∴CD=GD+CG=6+8=14(km).即公路CD的长为14 km.
(3)方案一铺设电缆的费用较低.
理由:由(2),得DE=CD-CE=14-6=8(km).
∴方案一的铺设费用为2(DE+AB)+4AD=40(万元).
方案二的铺设费用为2(CE+BC+AB)=32+8≈45.9(万元).
∵45.9>40,∴方案一铺设电缆的费用较低.
基础训练
知识点1 利用解直角三角形解一般三角形应用问题
1.为解决停车难的问题,在如图所示的一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出___________个这样的停车位.
2.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,在D点测得∠ADB=60°,又CD=60 m,则河宽AB为___________m.(结果保留根号)?2·1·c·n·j·y
3.如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长是 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)21·世纪*教育网
4.长为4m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了 m.【来源:21cnj*y.co*m】
5.如图,是意大利著名的比萨斜塔,塔身的中心线与垂直中心线的夹角A约为5°28',塔身AB的长为54.5 m,则塔顶中心偏离垂直中心线的距离BC是( )【出处:21教育名师】
A.54.5×sin 5°28'm B.54.5×cos 5°28'm
C.54.5×tan 5°28'm D. m
6.如图,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )www-2-1-cnjy-com
A.asin 40°米 B.acos 40°米
C.atan 40°米 D.米
知识点2 利用解直角三角形解与圆相关的问题
7.如图,某航天飞机在地球表面点P的正上方A处,从A处观测地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P,Q两点间的地面距离分别是( )2-1-c-n-j-y
A.,
B.-R,
C.-R,
D.-R,
8.如图,在半径为5的☉O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为 .21世纪教育网版权所有
9.为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图(如图所示).按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.为标明限高,请根据图形求CE的长.(参考数据:sin 18°≈0.31,cos 18°≈0.95,结果精确到0.1 m)21*cnjy*com
提升训练
命题角度1 利用解直角三角形测实际中的距离(化斜为直法)
10.如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.www.21-cn-jy.com
(1)求改直后的公路AB的长;
(2)问:公路改直后比原来缩短了多少千米?(sin 25°≈0.42,cos 25°≈0.91,sin 37°≈0.60,tan 37°≈0.75)21·cn·jy·com
命题角度2 利用解直角三角形测下降高度
11.如图,这是一把可调节座椅的侧面示意图,已知头枕上的点到调节器点O处的距离为80 cm,AO与地面垂直,现调整靠背,把OA绕点O旋转35°到OA'处,求调整后点A'比调整前点A的高度降低了多少厘米?(结果取整数)【来源:21·世纪·教育·网】
(参考数据:sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70)
探究培优
拔尖角度 利用解直角三角形解方案设计问题
12.如图所示,A,B为两个村庄,AB,BC,CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直.现在要从点E处开始铺设通往村庄A、村庄B的一条电线,共有如下两种铺设方案:21cnjy.com
方案一:E→D→A→B;方案二:E→C→B→A.
经测量得AB=4 km,BC=10 km,CE=6 km,∠BDC=45°,∠ABD=15°.已
知地上电缆的修建费为2万元/km,水下电缆的修建费为4万元/km.
(1)求出河宽AD.(结果保留根号)
(2)求出公路CD的长.
(3)哪种方案铺设电缆的费用较低?请说明理由.
参考答案
1.【答案】17 2.【答案】30 3.【答案】
4.【答案】2(-)
5.【答案】A 6.【答案】C 7.【答案】B
8.【答案】8或或
解:(1)当AB=AP时,如图①,作OH⊥AB于点H,延长AO交PB于点G;
易知=cos∠APC=cos∠AOH==?PC=AP=.
又知PG===?BC=PC-2PG=-=.
(2)当PA=PB时,如图②,延长PO交AB于点K,易知
OK=3,PK=8,PB=PA=4,
易知=cos ∠APC=cos∠AOK==?PC=AP=?BC=PC-PB=
(3)当BA=BP时,如图③,由∠C=90°-∠P=90°-∠PAB=∠CAB?BC=AB=8.
综上:BC=8或或.
9.解:在Rt△ABD中,AB=9 m,∠BAE=18°,
∴BD=AB·tan ∠BAE=9tan 18°(m).
∴CD=BD-BC=(9tan 18°-0.5)m.
∵∠CDE=90°-∠BAE=90°-∠DCE,
∴∠DCE=∠BAE=18°.
在Rt△CDE中,有cos ∠DCE=,
∴CE=CD·cos 18°=(9tan 18°-0.5)×cos 18°
=9××cos 18°-0.5cos 18°
=9sin 18°-0.5cos 18°
≈9×0.31-0.5×0.95
=2.315≈2.3(m).
分析:解此类题的关键是构造数学模型,将求限高的问题转化为解直角三角形的问题.此外,为了安全,此处宜用去尾法取近似值.
10.解:(1)作CH⊥AB于点H,在Rt△ACH中,CH=AC·sin ∠CAB=AC·sin 25°≈10×0.42=4.2(千米),21教育网
AH=AC·cos ∠CAB=AC·cos 25°≈10×0.91=9.1(千米).
在Rt△BCH中,BH=≈=5.6(千米).
∴AB=AH+BH≈9.1+5.6=14.7(千米).
(2)BC=≈=7.0(千米),
∴AC+BC-AB≈10+7.0-14.7=2.3(千米).
∴公路改直后比原来缩短了约2.3千米.
11.解:过点A'作A'H⊥OA于点H,
由旋转可知,OA'=OA=80 cm,
在Rt△OA'H中,OH=OA'cos 35°≈80×0.82=65.6(cm).
∴AH=OA-OH≈80-65.6=14.4≈14(cm).
答:调整后点A'比调整前点A的高度降低了14 cm.
12.解:(1)如图,过点B作BF⊥AD,交DA的延长线于点F.
∵CD⊥AD,∠BDC=45°,∴∠BDF=45°.
在Rt△BFA中,∠BAF=∠ABD+∠BDF=15°+45°=60°,
∴BF=AB·sin 60°=4×=6(km),AF=AB·cos 60°=4×
=2(km).
在Rt△BFD中,∵∠BDF=45°,∴DF=BF=6 km.
∴AD=DF-AF=(6-2)km.即河宽AD为(6-2)km.
(2)如图,过点B作BG⊥CD于点G,易证四边形BFDG是正方形,∴BG=GD=BF=6 km.
在Rt△BGC中,CG===8(km),
∴CD=GD+CG=6+8=14(km).即公路CD的长为14 km.
(3)方案一铺设电缆的费用较低.
理由:由(2),得DE=CD-CE=14-6=8(km).
∴方案一的铺设费用为2(DE+AB)+4AD=40(万元).
方案二的铺设费用为2(CE+BC+AB)=32+8≈45.9(万元).
∵45.9>40,∴方案一铺设电缆的费用较低.
