29.3 课题学习 制作立体模型 同步练习
文档属性
| 名称 | 29.3 课题学习 制作立体模型 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 538.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 22:44:37 | ||
图片预览

文档简介
29.3 课题学习 制作立体模型
基础训练
知识点1 由实物图到三视图的认识
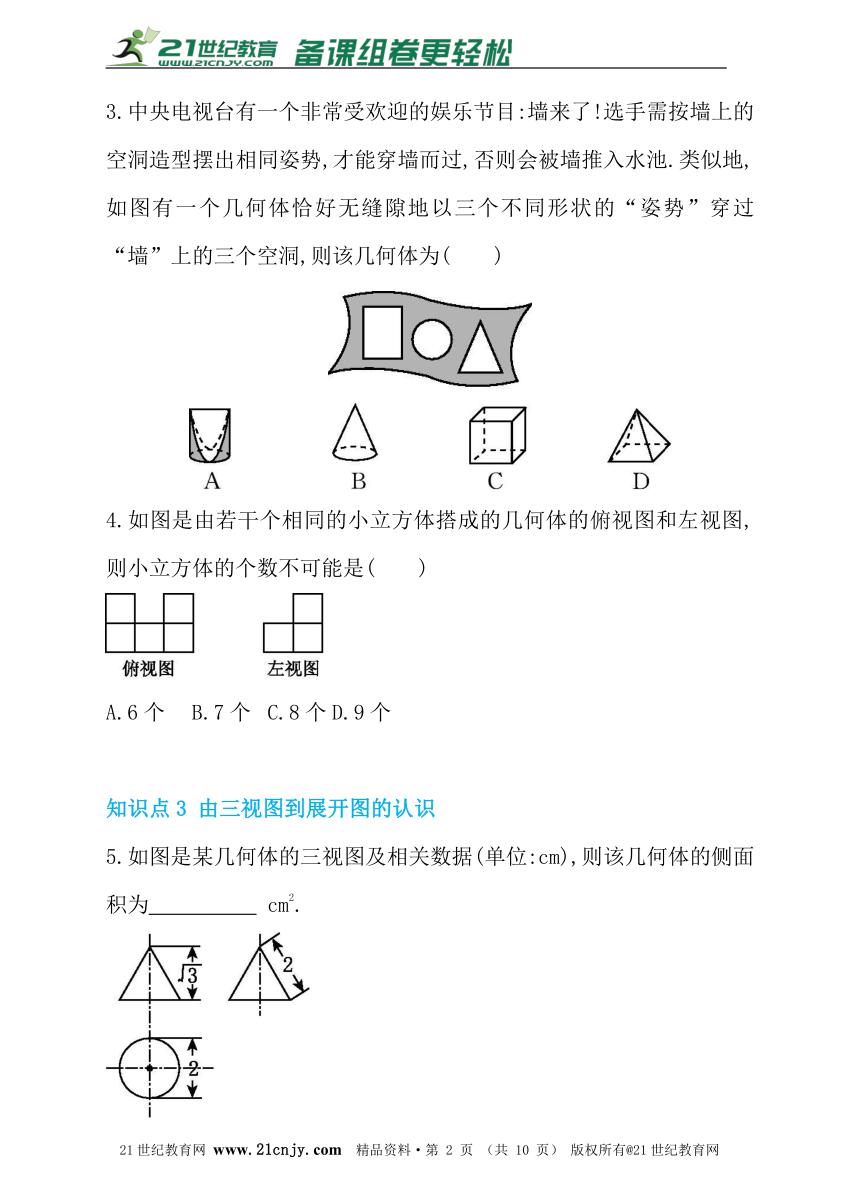
1.如果用表示1个小立方体,用表示两个小立方体叠加,用表示三个小立方体叠加,那么下面由7个小立方体搭成的几何体,从正前方观察,可画出的平面图形是( )www.21-cn-jy.com
2.如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
知识点2 由三视图到立体图的认识
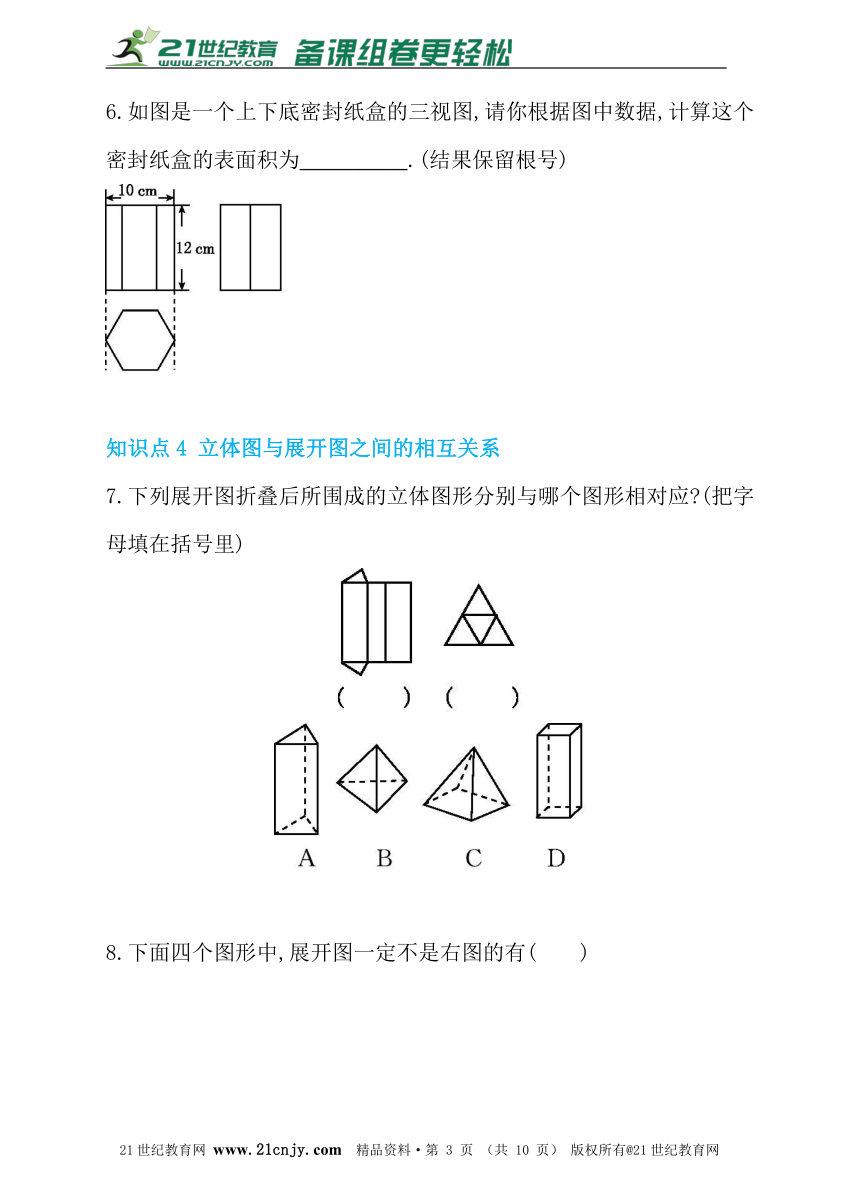
3.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,如图有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )21·世纪*教育网
4.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )
A.6个 B.7个 C.8个 D.9个
知识点3 由三视图到展开图的认识
5.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为__________ cm2.www-2-1-cnjy-com
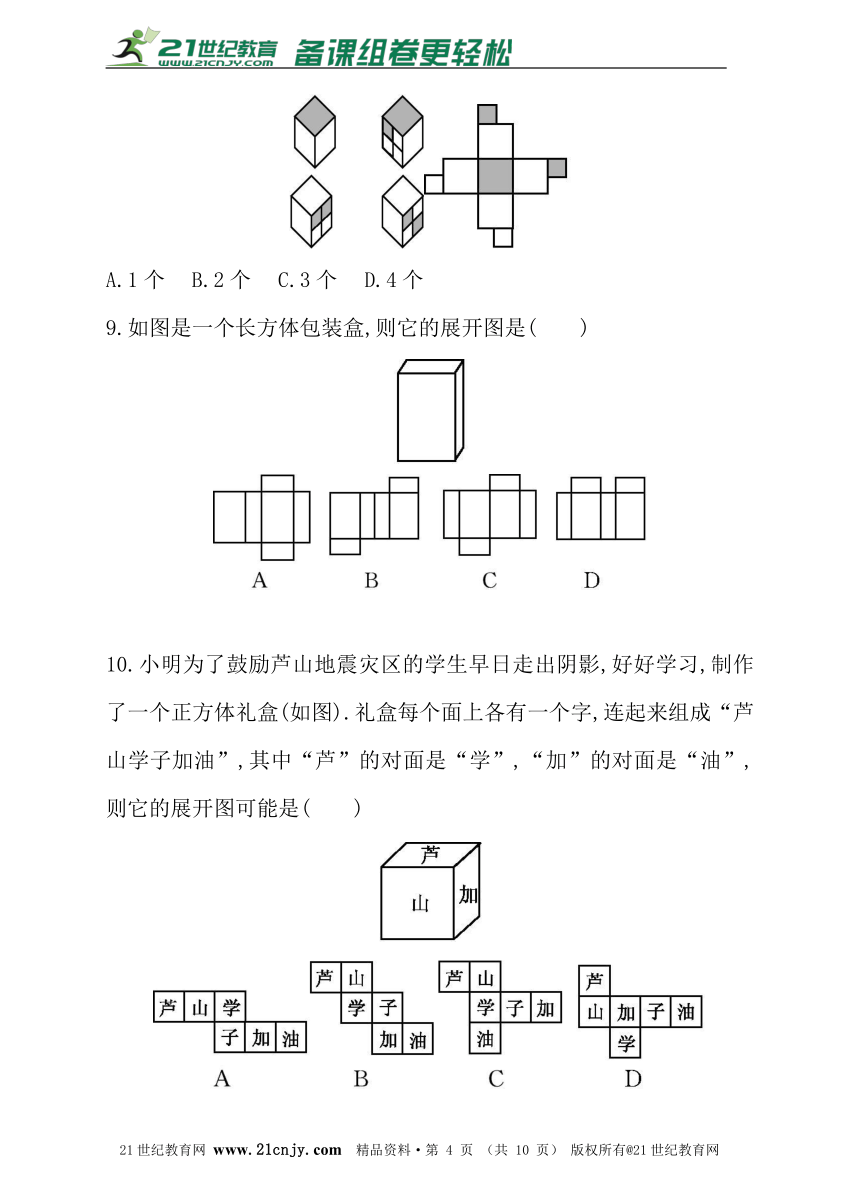
6.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为__________.(结果保留根号)2-1-c-n-j-y
知识点4 立体图与展开图之间的相互关系
7.下列展开图折叠后所围成的立体图形分别与哪个图形相对应?(把字母填在括号里)
8.下面四个图形中,展开图一定不是右图的有( )
A.1个 B.2个 C.3个 D.4个
9.如图是一个长方体包装盒,则它的展开图是( )
10.小明为了鼓励芦山地震灾区的学生早日走出阴影,好好学习,制作了一个正方体礼盒(如图).礼盒每个面上各有一个字,连起来组成“芦山学子加油”,其中“芦”的对面是“学”,“加”的对面是“油”,则它的展开图可能是( )21·cn·jy·com
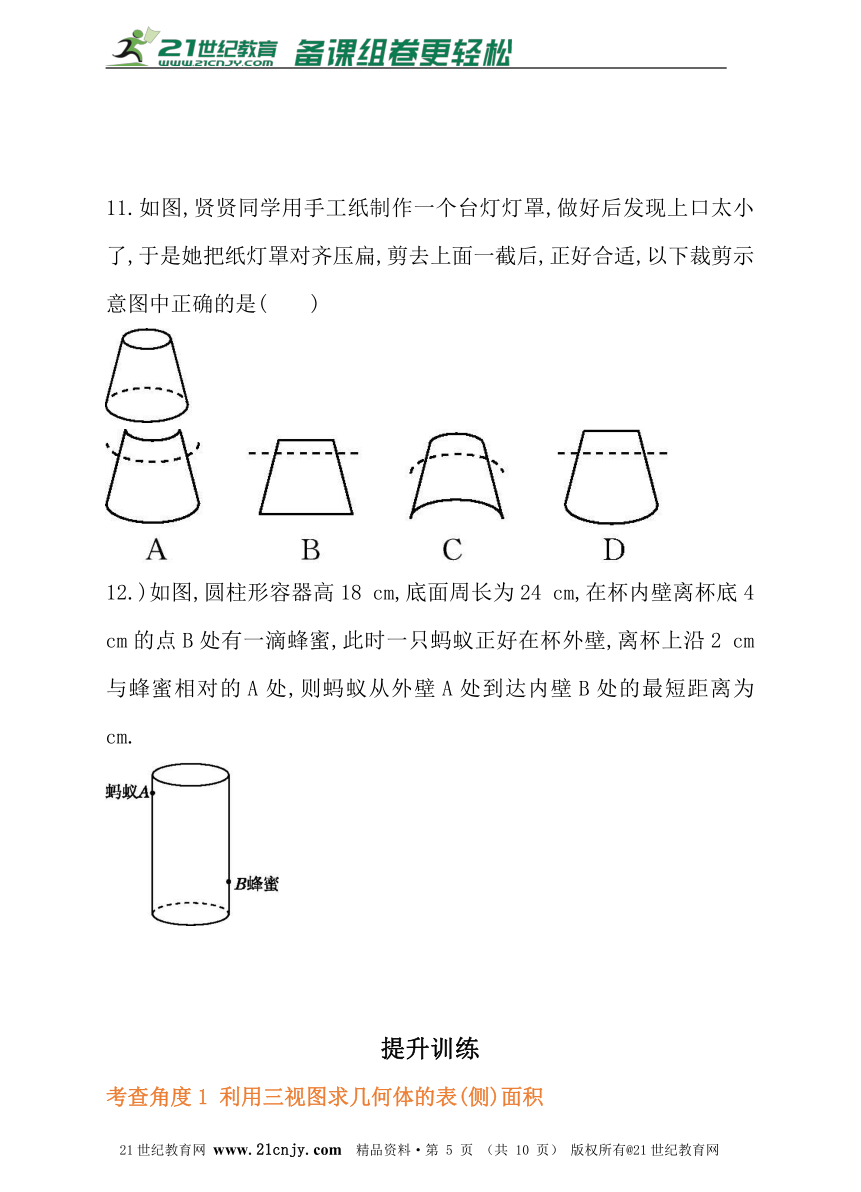
11.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是她把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中正确的是( )21cnjy.com
12.)如图,圆柱形容器高18 cm,底面周长为24 cm,在杯内壁离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2 cm与蜂蜜相对的A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm.2·1·c·n·j·y
提升训练
考查角度1 利用三视图求几何体的表(侧)面积
13.某工厂要加工一批密封罐,设计者给出了物体的三种视图(单位:cm),如图所示,请你按照三种视图求制作每个密封罐所需钢板的面积(结果保留整数).21*cnjy*com
14.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据,求出它的侧面积.
考查角度2 利用模具画其三视图和展开图
15.小明利用废纸板制作一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示(有盖),有关数据已标注在图上.21教育网
(1)请画出该立体模型的三视图和展开图;
(2)制作该笔筒至少要用多少废纸板?
参考答案
1.【答案】B
解:从正面看这个几何体,第一层的左边是一个小立方体,中间是三个小立方体,右边是一个小立方体;第二层只有中间有两个小立方体,故选B.【来源:21cnj*y.co*m】
2.【答案】A
3.【答案】A
解:比较各几何体的三视图,考虑是否有长方形、圆、三角形即可.对于A,三视图的形状分别为长方形、三角形、圆,符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意.故选A.【出处:21教育名师】
4.【答案】D
解:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2.
当a,b,c中有一个为2时,小立方体的个数为:1+1+2+1+1=6;当a,b,c中有两个为2时,小立方体的个数为:1+1+2+2+1=7;当a,b,c都为2时,小立方体的个数为:1+1+2+2+2=8.所以小立方体的个数可能为6个、7个或8个.【版权所有:21教育】
5.【答案】2π
解:由三视图可知,此几何体是圆锥,母线长为2 cm,底面直径为2 cm,高是 cm,其侧面展开图为扇形,所以其侧面积为扇形的面积S=×2π×2=2π(cm2).【来源:21·世纪·教育·网】
6.【答案】(75+360) cm2
解:据图形得,纸盒的底面为正六边形,正六边形的边长为5 cm,纸盒的高为12 cm.每个底面正六边形的面积=6××52=(cm2);侧面展开图为长方形,侧面积为30×12=360(cm2),所以这个密封纸盒的表面积=2×+360=(75+360)(cm2).21教育名师原创作品
解决三视图问题时,应熟悉常见的几何体的三视图;计算正六棱柱的表面积时注意是2个底面积加上侧面积.
7.【答案】A;B
解:A.从图中可知组成的立体图形一共有5个面,3个长方形,2个三角形,符合题图中的第一幅图;B.组成的立体图形一共有4个面,每个面都是三角形,符合题图中的第二幅图.21*cnjy*com
8.【答案】B
9.【答案】A
解:A可以拼成一个长方体;B,C,D不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
10.【答案】D
11.【答案】A
解:圆台的侧面展开图是扇环,折叠之后是展开图的一半,其不等的两条曲线必是向内弯的,故选A.
12.【答案】20
13.解:由三种视图可知,密封罐的形状是正六棱柱,如图①所示.罐子的高为50 cm,底面边长为50 cm,图②是它的展开图.
由展开图可知,制作这样一个密封罐所需钢板的面积为
6×50×50+2×6××50×50×=6×502×≈27 990(cm2).
方法总结:由几何体的三视图求它的表面积的方法:先由几何体的三视图想象出该几何体的形状,再进一步画出展开图,从而计算出表面积.
14.解:四棱柱.由三视图知,棱柱底面菱形的对角线长分别是4 cm,3 cm,∴菱形边长为cm,其侧面积=×8×4=80(cm2).21世纪教育网版权所有
15.解:(1)展开图如图①所示.
三视图如图②所示.
①
②
(2)(6+8+10)×14+6×8÷2=360(cm2).
答:制作该笔筒至少要用360 cm2废纸板.
基础训练
知识点1 由实物图到三视图的认识
1.如果用表示1个小立方体,用表示两个小立方体叠加,用表示三个小立方体叠加,那么下面由7个小立方体搭成的几何体,从正前方观察,可画出的平面图形是( )www.21-cn-jy.com
2.如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
知识点2 由三视图到立体图的认识
3.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,如图有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )21·世纪*教育网
4.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是( )
A.6个 B.7个 C.8个 D.9个
知识点3 由三视图到展开图的认识
5.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为__________ cm2.www-2-1-cnjy-com
6.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为__________.(结果保留根号)2-1-c-n-j-y
知识点4 立体图与展开图之间的相互关系
7.下列展开图折叠后所围成的立体图形分别与哪个图形相对应?(把字母填在括号里)
8.下面四个图形中,展开图一定不是右图的有( )
A.1个 B.2个 C.3个 D.4个
9.如图是一个长方体包装盒,则它的展开图是( )
10.小明为了鼓励芦山地震灾区的学生早日走出阴影,好好学习,制作了一个正方体礼盒(如图).礼盒每个面上各有一个字,连起来组成“芦山学子加油”,其中“芦”的对面是“学”,“加”的对面是“油”,则它的展开图可能是( )21·cn·jy·com
11.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是她把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中正确的是( )21cnjy.com
12.)如图,圆柱形容器高18 cm,底面周长为24 cm,在杯内壁离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2 cm与蜂蜜相对的A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm.2·1·c·n·j·y
提升训练
考查角度1 利用三视图求几何体的表(侧)面积
13.某工厂要加工一批密封罐,设计者给出了物体的三种视图(单位:cm),如图所示,请你按照三种视图求制作每个密封罐所需钢板的面积(结果保留整数).21*cnjy*com
14.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据,求出它的侧面积.
考查角度2 利用模具画其三视图和展开图
15.小明利用废纸板制作一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示(有盖),有关数据已标注在图上.21教育网
(1)请画出该立体模型的三视图和展开图;
(2)制作该笔筒至少要用多少废纸板?
参考答案
1.【答案】B
解:从正面看这个几何体,第一层的左边是一个小立方体,中间是三个小立方体,右边是一个小立方体;第二层只有中间有两个小立方体,故选B.【来源:21cnj*y.co*m】
2.【答案】A
3.【答案】A
解:比较各几何体的三视图,考虑是否有长方形、圆、三角形即可.对于A,三视图的形状分别为长方形、三角形、圆,符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意.故选A.【出处:21教育名师】
4.【答案】D
解:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2.
当a,b,c中有一个为2时,小立方体的个数为:1+1+2+1+1=6;当a,b,c中有两个为2时,小立方体的个数为:1+1+2+2+1=7;当a,b,c都为2时,小立方体的个数为:1+1+2+2+2=8.所以小立方体的个数可能为6个、7个或8个.【版权所有:21教育】
5.【答案】2π
解:由三视图可知,此几何体是圆锥,母线长为2 cm,底面直径为2 cm,高是 cm,其侧面展开图为扇形,所以其侧面积为扇形的面积S=×2π×2=2π(cm2).【来源:21·世纪·教育·网】
6.【答案】(75+360) cm2
解:据图形得,纸盒的底面为正六边形,正六边形的边长为5 cm,纸盒的高为12 cm.每个底面正六边形的面积=6××52=(cm2);侧面展开图为长方形,侧面积为30×12=360(cm2),所以这个密封纸盒的表面积=2×+360=(75+360)(cm2).21教育名师原创作品
解决三视图问题时,应熟悉常见的几何体的三视图;计算正六棱柱的表面积时注意是2个底面积加上侧面积.
7.【答案】A;B
解:A.从图中可知组成的立体图形一共有5个面,3个长方形,2个三角形,符合题图中的第一幅图;B.组成的立体图形一共有4个面,每个面都是三角形,符合题图中的第二幅图.21*cnjy*com
8.【答案】B
9.【答案】A
解:A可以拼成一个长方体;B,C,D不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
10.【答案】D
11.【答案】A
解:圆台的侧面展开图是扇环,折叠之后是展开图的一半,其不等的两条曲线必是向内弯的,故选A.
12.【答案】20
13.解:由三种视图可知,密封罐的形状是正六棱柱,如图①所示.罐子的高为50 cm,底面边长为50 cm,图②是它的展开图.
由展开图可知,制作这样一个密封罐所需钢板的面积为
6×50×50+2×6××50×50×=6×502×≈27 990(cm2).
方法总结:由几何体的三视图求它的表面积的方法:先由几何体的三视图想象出该几何体的形状,再进一步画出展开图,从而计算出表面积.
14.解:四棱柱.由三视图知,棱柱底面菱形的对角线长分别是4 cm,3 cm,∴菱形边长为cm,其侧面积=×8×4=80(cm2).21世纪教育网版权所有
15.解:(1)展开图如图①所示.
三视图如图②所示.
①
②
(2)(6+8+10)×14+6×8÷2=360(cm2).
答:制作该笔筒至少要用360 cm2废纸板.
