第8章 一元一次不等式 单元测试卷
文档属性
| 名称 | 第8章 一元一次不等式 单元测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 467.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-09 00:00:00 | ||
图片预览




文档简介
第8章 一元一次不等式 单元测试卷
一、选择题(每题3分,共30分)
1.若a>b,则( )
A.ac>bc B.->-
C.-a<-b D.a-22.某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是( )
A.t>33 B.t≤24 C.243.已知a,b为常数,若ax+b>0的解集是x<,则bx-a<0的解集是( )
A.x>-3 B.x<-3 C.x>3 D.x<3
4.不等式组的解集在数轴上表示正确的是( )
5.不等式2-3x≥2x-8的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
6.不等式组的最小整数解为( )
A.-1 B.0 C.1 D.2
7.使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
A.3,4 B.4,5 C.3,4,5 D.不存在
8.某种植物适宜生长在温度为18℃~20℃的山区,已知山区海拔每升高100米,气温下降0.55℃,现测得山脚下(海拔高度为0米)的气温为22℃,问该植物种在山上的什么地方较适宜.如果设该植物种在海拔高度为x米的山区较适宜,则由题意可列出的不等式组为( )
A.18≤22-×x≤20 B.18≤22-≤20
C.18≤22-0.55x≤20 D.18≤22-≤20
9.若关于x的一元一次不等式组无解,则a的取值范围是( )
A.a≥1 B.a>1 C.a≤-1 D.a<-1
10.已知水在0 ℃以下就会结冰,某天气温是零下10 ℃,湖面开始结冰,冰块厚度以2 mm/h的速度增加,同时冰块厚度又以0.2 mm/h的速度升华减少,若人在湖面上可以安全行走,要求冰块厚度至少是18 mm,则从开始结冰至人能在湖面上安全行走至少需( )
A.7 h B.8 h C.9 h D.10 h
二、填空题(每题3分,共30分)
11.当a<0时,6+a___________6-a(填“<”或“>”).?
12.已知关于x的不等式(1+a)x<3的解集为x>,则a的取值范围是___________.?
13.定义一种法则“⊕”如下:a⊕b=例如:1⊕2=2,若(-2m-5)⊕3=3,则m的取值范围是___________.?21·cn·jy·com
14.若m15.若关于x,y的二元一次方程组的解满足x+y>1,则k的取值范围是__________.?
16.如图,要使输出值y大于100,则输入的最小正整数x是__________.
17.若关于x的不等式组的解集中任何一个x的值均不在2≤x≤5的范围内,则a的取值范围是__________.?www.21-cn-jy.com
18.孙泽坤想给宋沂儒打电话,但忘记了电话号码中的一位数字,只记得号码是521 689( 表示忘记的数字).若 位置的数字是不等式组的整数解,则 可能表示的数字是__________.?
19.若关于x的不等式(2a-b)x+a-5b>0的解集是x<,则关于x的不等式(a-b)x>b的解集是__________.?2·1·c·n·j·y
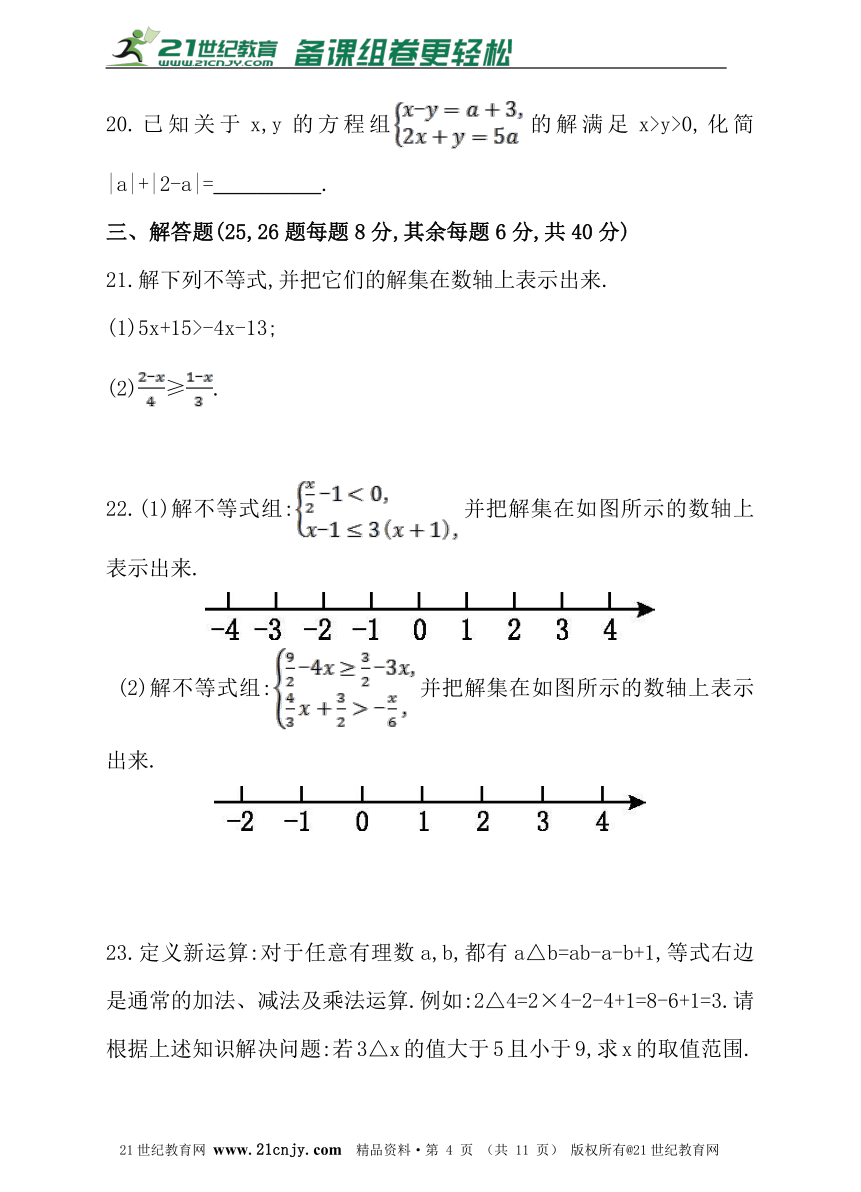
20.已知关于x,y的方程组的解满足x>y>0,化简|a|+|2-a|=__________.?
三、解答题(25,26题每题8分,其余每题6分,共40分)
21.解下列不等式,并把它们的解集在数轴上表示出来.
(1)5x+15>-4x-13;
(2)≥.
22.(1)解不等式组:并把解集在如图所示的数轴上表示出来.
(2)解不等式组:并把解集在如图所示的数轴上表示出来.
23.定义新运算:对于任意有理数a,b,都有a△b=ab-a-b+1,等式右边是通常的加法、减法及乘法运算.例如:2△4=2×4-2-4+1=8-6+1=3.请根据上述知识解决问题:若3△x的值大于5且小于9,求x的取值范围.
24.某商家计划从厂家采购空调和冰箱两种产品共20台.空调的采购单价y(元)与采购数量x(台)满足y=-20x+1500(025.求不等式(2x-1)(x+3)>0的解集.
解:根据“同号两数相乘,积为正”可得:①或②
解①得x>;解②得x<-3.
所以原不等式的解集为x>或x<-3.
请你仿照上述方法解决下列问题:
(1)求不等式(2x-3)(x+1)<0的解集;
(2)求不等式≥0的解集.
26.为打造“书香校园”某学校计划用不超过1 900本科技类书籍和1 620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.21·世纪*教育网
(1)问符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明在(1)中哪种方案费用最低?最低费用是多少元?
参考答案
一、1.【答案】C 2.【答案】D 3.【答案】B 4.【答案】C
5.【答案】C
解:移项,得-3x-2x≥-8-2,合并同类项,得-5x≥-10,则x≤2.故非负整数解是0,1,2,共3个.www-2-1-cnjy-com
6.【答案】B
解:不等式组的解集为-17.【答案】A
解:根据题意得:解得3≤x<5,则x的整数值是3,4,故选A.
8.【答案】A
解:海拔每升高100米,气温下降0.55℃,那么海拔每升高1米,气温下降℃;海拔高度为x米,则升高了x米,气温就在22℃的基础上下降x×℃ ,而温度适宜的范围是18℃~20℃.故选A.
9.【答案】A
10.【答案】D
解:设从开始结冰至人能在湖面上安全行走需x h,根据题意得(2-0.2)x≥18,解得x≥10,即从开始结冰至人能在湖面上安全行走至少需10 h.21世纪教育网版权所有
二、11.【答案】<
解:∵a<0,∴a<-a,在不等式两边同时加上6,得6+a<6-a.
12.【答案】a<-1
解:由题意得1+a<0,移项,得a<-1.
13.【答案】m≥-4
解:由题意得-2m-5≤3,解得m≥-4.
14.【答案】m-115.【答案】k>2
解:①+②,得3(x+y)=3k-3,解得x+y=k-1,∵x+y>1,∴k-1>1,解得k>2.2-1-c-n-j-y
16.【答案】21
解:若x为偶数,根据题意,得x×4+13>100,解得x>,此时x的最小整数值为22;若x为奇数,根据题意,得x×5>100,解得x>20,此时x的最小整数值为21,综上所述,输入的最小正整数x是21.
17.【答案】a≥5或a≤1
解:解关于x的不等式组,得a18.【答案】6,7,8
19.【答案】x<
解:∵(2a-b)x+a-5b>0的解集是
x<,∴2a-b<0,x<,
∴=,解得a=b,
∵2a-b<0,∴2×b-b<0,解得b<0,
∴(a-b)x>b转化为x>b,
整理得bx>b.∵b<0,∴x<.
20.【答案】2a-2
三、21.解:(1)移项、合并同类项,得9x>-28,
两边都除以9,得x>-.
表示在数轴上如图所示.
(2)去分母,得3(2-x)≥4(1-x),
去括号,得6-3x≥4-4x,
移项、合并同类项,得x≥-2.表示在数轴上如图所示.
22.解:(1)
由①得x<2,
由②得x≥-2,
所以,不等式组的解集是-2≤x<2.
在数轴上的表示如图所示.
(2)由①得x≤3,
由②得x>-1,
所以不等式组的解集是-1在数轴上的表示如图所示:
23.解:由题意得,3△x=3x-3-x+1=2x-2,
则解得24.解:根据题意可得
解得11≤x≤15,因为x为整数,
所以x可取的值为11,12,13,14,15.
所以该商家共有5种采购方案.
25.解:(1)根据“异号两数相乘,积为负”可得:
①或②
解不等式组①得无解,解不等式组②得-1所以原不等式的解集为-1(2)依题意可得①或②
解①得x≥3,解②得x<-2,
所以原不等式的解集为x≥3或x<-2.
26.解:(1)设组建中型图书角x个,则组建小型图书角(30-x)个.
由题意得
解这个不等式组得18≤x≤20.
由于x只能取整数,所以x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;
当x=20时,30-x=10.
故有三种组建方案:方案一,组建中型图书角18个,小型图书角12个;方案二,组建中型图书角19个,小型图书角11个;方案三,组建中型图书角20个,小型图书角10个.21教育网
(2)方法一:由于组建一个中型图书角的费用大于组建一个小型图书角的费用,因此组建中型图书角的数量越少,费用就越低,故方案一费用最低,21cnjy.com
最低费用是860×18+570×12=22320(元).
方法二:①方案一的费用是:860×18+570×12=22320(元).
②方案二的费用是:860×19+570×11=22610(元).
③方案三的费用是:860×20+570×10=22900(元).
故方案一费用最低,最低费用是22320元.
一、选择题(每题3分,共30分)
1.若a>b,则( )
A.ac>bc B.->-
C.-a<-b D.a-2
A.t>33 B.t≤24 C.24
A.x>-3 B.x<-3 C.x>3 D.x<3
4.不等式组的解集在数轴上表示正确的是( )
5.不等式2-3x≥2x-8的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
6.不等式组的最小整数解为( )
A.-1 B.0 C.1 D.2
7.使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
A.3,4 B.4,5 C.3,4,5 D.不存在
8.某种植物适宜生长在温度为18℃~20℃的山区,已知山区海拔每升高100米,气温下降0.55℃,现测得山脚下(海拔高度为0米)的气温为22℃,问该植物种在山上的什么地方较适宜.如果设该植物种在海拔高度为x米的山区较适宜,则由题意可列出的不等式组为( )
A.18≤22-×x≤20 B.18≤22-≤20
C.18≤22-0.55x≤20 D.18≤22-≤20
9.若关于x的一元一次不等式组无解,则a的取值范围是( )
A.a≥1 B.a>1 C.a≤-1 D.a<-1
10.已知水在0 ℃以下就会结冰,某天气温是零下10 ℃,湖面开始结冰,冰块厚度以2 mm/h的速度增加,同时冰块厚度又以0.2 mm/h的速度升华减少,若人在湖面上可以安全行走,要求冰块厚度至少是18 mm,则从开始结冰至人能在湖面上安全行走至少需( )
A.7 h B.8 h C.9 h D.10 h
二、填空题(每题3分,共30分)
11.当a<0时,6+a___________6-a(填“<”或“>”).?
12.已知关于x的不等式(1+a)x<3的解集为x>,则a的取值范围是___________.?
13.定义一种法则“⊕”如下:a⊕b=例如:1⊕2=2,若(-2m-5)⊕3=3,则m的取值范围是___________.?21·cn·jy·com
14.若m
16.如图,要使输出值y大于100,则输入的最小正整数x是__________.
17.若关于x的不等式组的解集中任何一个x的值均不在2≤x≤5的范围内,则a的取值范围是__________.?www.21-cn-jy.com
18.孙泽坤想给宋沂儒打电话,但忘记了电话号码中的一位数字,只记得号码是521 689( 表示忘记的数字).若 位置的数字是不等式组的整数解,则 可能表示的数字是__________.?
19.若关于x的不等式(2a-b)x+a-5b>0的解集是x<,则关于x的不等式(a-b)x>b的解集是__________.?2·1·c·n·j·y
20.已知关于x,y的方程组的解满足x>y>0,化简|a|+|2-a|=__________.?
三、解答题(25,26题每题8分,其余每题6分,共40分)
21.解下列不等式,并把它们的解集在数轴上表示出来.
(1)5x+15>-4x-13;
(2)≥.
22.(1)解不等式组:并把解集在如图所示的数轴上表示出来.
(2)解不等式组:并把解集在如图所示的数轴上表示出来.
23.定义新运算:对于任意有理数a,b,都有a△b=ab-a-b+1,等式右边是通常的加法、减法及乘法运算.例如:2△4=2×4-2-4+1=8-6+1=3.请根据上述知识解决问题:若3△x的值大于5且小于9,求x的取值范围.
24.某商家计划从厂家采购空调和冰箱两种产品共20台.空调的采购单价y(元)与采购数量x(台)满足y=-20x+1500(0
解:根据“同号两数相乘,积为正”可得:①或②
解①得x>;解②得x<-3.
所以原不等式的解集为x>或x<-3.
请你仿照上述方法解决下列问题:
(1)求不等式(2x-3)(x+1)<0的解集;
(2)求不等式≥0的解集.
26.为打造“书香校园”某学校计划用不超过1 900本科技类书籍和1 620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.21·世纪*教育网
(1)问符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明在(1)中哪种方案费用最低?最低费用是多少元?
参考答案
一、1.【答案】C 2.【答案】D 3.【答案】B 4.【答案】C
5.【答案】C
解:移项,得-3x-2x≥-8-2,合并同类项,得-5x≥-10,则x≤2.故非负整数解是0,1,2,共3个.www-2-1-cnjy-com
6.【答案】B
解:不等式组的解集为-1
解:根据题意得:解得3≤x<5,则x的整数值是3,4,故选A.
8.【答案】A
解:海拔每升高100米,气温下降0.55℃,那么海拔每升高1米,气温下降℃;海拔高度为x米,则升高了x米,气温就在22℃的基础上下降x×℃ ,而温度适宜的范围是18℃~20℃.故选A.
9.【答案】A
10.【答案】D
解:设从开始结冰至人能在湖面上安全行走需x h,根据题意得(2-0.2)x≥18,解得x≥10,即从开始结冰至人能在湖面上安全行走至少需10 h.21世纪教育网版权所有
二、11.【答案】<
解:∵a<0,∴a<-a,在不等式两边同时加上6,得6+a<6-a.
12.【答案】a<-1
解:由题意得1+a<0,移项,得a<-1.
13.【答案】m≥-4
解:由题意得-2m-5≤3,解得m≥-4.
14.【答案】m-1
解:①+②,得3(x+y)=3k-3,解得x+y=k-1,∵x+y>1,∴k-1>1,解得k>2.2-1-c-n-j-y
16.【答案】21
解:若x为偶数,根据题意,得x×4+13>100,解得x>,此时x的最小整数值为22;若x为奇数,根据题意,得x×5>100,解得x>20,此时x的最小整数值为21,综上所述,输入的最小正整数x是21.
17.【答案】a≥5或a≤1
解:解关于x的不等式组,得a
19.【答案】x<
解:∵(2a-b)x+a-5b>0的解集是
x<,∴2a-b<0,x<,
∴=,解得a=b,
∵2a-b<0,∴2×b-b<0,解得b<0,
∴(a-b)x>b转化为x>b,
整理得bx>b.∵b<0,∴x<.
20.【答案】2a-2
三、21.解:(1)移项、合并同类项,得9x>-28,
两边都除以9,得x>-.
表示在数轴上如图所示.
(2)去分母,得3(2-x)≥4(1-x),
去括号,得6-3x≥4-4x,
移项、合并同类项,得x≥-2.表示在数轴上如图所示.
22.解:(1)
由①得x<2,
由②得x≥-2,
所以,不等式组的解集是-2≤x<2.
在数轴上的表示如图所示.
(2)由①得x≤3,
由②得x>-1,
所以不等式组的解集是-1
23.解:由题意得,3△x=3x-3-x+1=2x-2,
则解得
解得11≤x≤15,因为x为整数,
所以x可取的值为11,12,13,14,15.
所以该商家共有5种采购方案.
25.解:(1)根据“异号两数相乘,积为负”可得:
①或②
解不等式组①得无解,解不等式组②得-1
解①得x≥3,解②得x<-2,
所以原不等式的解集为x≥3或x<-2.
26.解:(1)设组建中型图书角x个,则组建小型图书角(30-x)个.
由题意得
解这个不等式组得18≤x≤20.
由于x只能取整数,所以x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;
当x=20时,30-x=10.
故有三种组建方案:方案一,组建中型图书角18个,小型图书角12个;方案二,组建中型图书角19个,小型图书角11个;方案三,组建中型图书角20个,小型图书角10个.21教育网
(2)方法一:由于组建一个中型图书角的费用大于组建一个小型图书角的费用,因此组建中型图书角的数量越少,费用就越低,故方案一费用最低,21cnjy.com
最低费用是860×18+570×12=22320(元).
方法二:①方案一的费用是:860×18+570×12=22320(元).
②方案二的费用是:860×19+570×11=22610(元).
③方案三的费用是:860×20+570×10=22900(元).
故方案一费用最低,最低费用是22320元.
