第9章 多边形 单元测试卷
图片预览



文档简介
第9章 多边形 单元测试卷
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的高总在三角形内部
C.三角形的高、中线、角平分线一定是三条不同的线段
D.三角形的中线在三角形内部
2.如图,AB∥CD,∠A=45°,∠C=28°, 则∠AEC的大小为( )
A.17° B.62°
C.63° D.73°
3.下列各组长度的线段,能组成三角形的是( )
A.2 cm,3 cm,4 cm B.2 cm,3 cm,5 cm
C.2 cm,5 cm,10 cm D.8 cm,4 cm,4 cm
4.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.设△ABC的三边长分别为a,b,c,其中a,b满足|a+b-4|+(a-b+2)2=0,则第三边的长c的取值范围是( )【来源:21·世纪·教育·网】
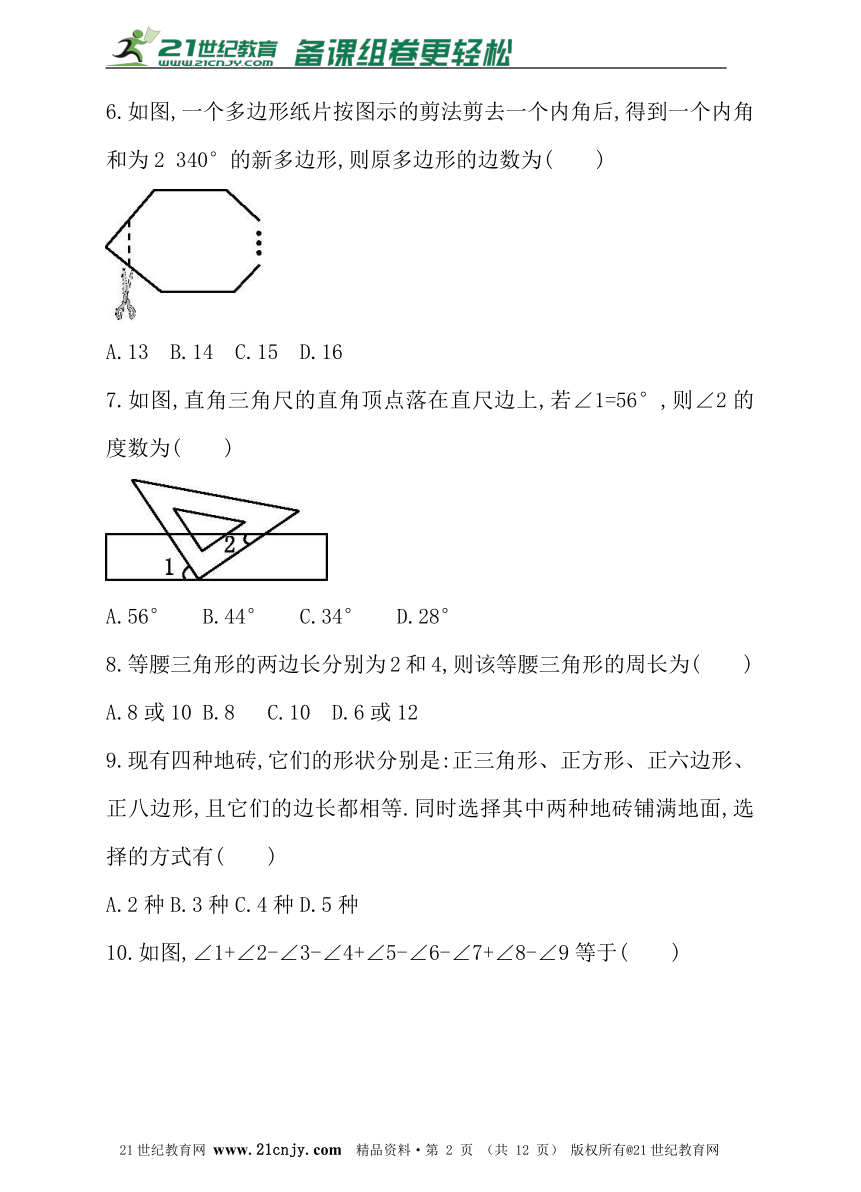
A.36.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2 340°的新多边形,则原多边形的边数为( )
A.13 B.14 C.15 D.16
7.如图,直角三角尺的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
8.等腰三角形的两边长分别为2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
9.现有四种地砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地砖铺满地面,选择的方式有( )2·1·c·n·j·y
A.2种 B.3种 C.4种 D.5种
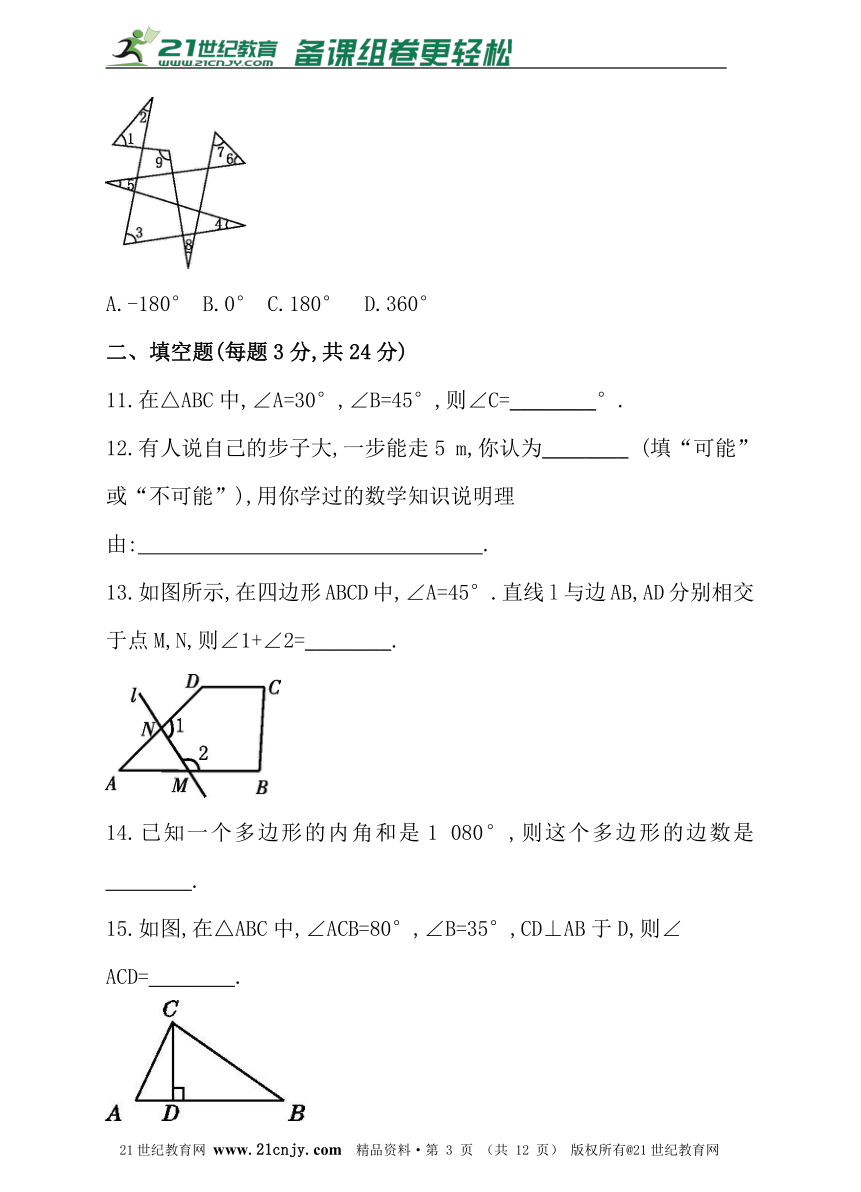
10.如图,∠1+∠2-∠3-∠4+∠5-∠6-∠7+∠8-∠9等于( )
A.-180° B.0° C.180° D.360°
二、填空题(每题3分,共24分)
11.在△ABC中,∠A=30°,∠B=45°,则∠C=________°.?
12.有人说自己的步子大,一步能走5 m,你认为________ (填“可能”或“不可能”),用你学过的数学知识说明理21·cn·jy·com
由: .?
13.如图所示,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2=________.21·世纪*教育网
14.已知一个多边形的内角和是1 080°,则这个多边形的边数是________.?
15.如图,在△ABC中,∠ACB=80°,∠B=35°,CD⊥AB于D,则∠
ACD=________.
16.n边形与m边形内角和度数的差为720°,则n与m的差为 .?
17.用4个完全一样的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图①,用n个完全一样的正六边形按这种方式进行拼接,如图②,若围成一圈后中间形成一个正多边形,则n的值为 .21教育网
18.如图所示,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 ,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2 012BC和∠A2 012CD的平分线交于点A2 013,得∠A2 013,则∠A2 013= °.
三、解答题(23,24题每题9分,其余每题7分,共46分)
19.求出图中x的值.
20.如图所示,BP平分∠FBC,CP平分∠ECB,∠A=40°,求∠BPC的度数.
21.有一张正方形桌面,它的4个内角的和为360°,现在锯掉它的一个角,残余桌面所有的内角的和是多少?小光说:“锯掉一个角,变成三角形,于是残余桌面所有的内角的和是180°.”小欣说:“锯掉一个角,变成五边形,内角和应为540°.”你认为谁对谁不对?说说你的解答.
22.如图,请你想办法求出五角星中∠A+∠B+∠C+∠D+∠E的值.下面是习题讲解时,老师和学生对话的情境:老师向学生抛出问题:观察图①中的图形,能分别求出∠A,∠B,∠C,∠D,∠E的度数吗?能的话怎么求?不能的话怎么办?学生通过观察回答:很明显每个角都不规则,因此求不出∠A,∠B,∠C,∠D,∠E的度数.有个学生小声地说了句:要是能把这五个角放到一块就好了.老师回答:有想法,就去试试看.很快就有学生发现利用三角形外角的性质将∠C与∠E的度数和,∠B与∠D的度数和分别用∠1和∠2表示.于是得到∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.根据以上信息,你能求出图②中∠A+∠B+∠C+∠D+∠E+∠F+∠G的值吗?21世纪教育网版权所有
23.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F,试说明:∠CEF=∠CFE.21cnjy.com
24.王老师准备装修新房的地面,到一家装修公司去看地砖,该公司现有一批边长相等的正多边形地砖(如图)供客户选择.
(1)若只用其中一种正多边形地砖铺满地面,则供王老师选择的正多边形地砖有哪些?
(2)若从其中任取两种组合,能铺满地面的正多边形地砖的组合有哪些?
(3)若从其中任取三种组合,能铺满地面的正多边形地砖的组合有哪些?
(4)请说出其中所蕴含的数学道理.
参考答案
一、1.【答案】D 2.【答案】D
3.【答案】A
解:根据三角形中任意两边之和大于第三边,任意两边之差小于第三边判断.
4.【答案】A
解:设多边形的边数是n,则(n-2)·180°=360°,解得n=4.
5.【答案】D
解:∵a,b满足|a+b-4|+(a-b+2)2=0,|a+b-4|≥0,(a-b+2)2≥0,∴a+b-4=0,a-b+2=0.∴a=1,b=3.∴c的取值范围为3-16.【答案】B 7.【答案】C
8.【答案】C
解:本题利用分类讨论思想解题,对于已知中没有明确腰和底边的题目一定要分类讨论,还应验证各种情况是否能构成三角形,这点非常重要,也是解题的关键.21*cnjy*com
9.【答案】B
解:可选择的方式有:正三角形和正方形;正三角形和正六边形;正方形和正八边形,共3种.
10.【答案】A
解:如图,
∵∠1+∠2=180°-∠α,∠3+∠4=180°-∠γ,∠5=180°-∠γ-∠θ,∠6+∠7=180°-∠β,∠8=180°-∠β-∠λ,∠9=360°-∠α-∠θ-∠λ,∴∠1+∠2-∠3-∠4+∠5-∠6-∠7+∠8-∠9=180°-∠α-(180°-∠γ)+180°-∠γ-∠θ-(180°-∠β)+180°-∠β-∠λ-(360°-∠α-∠θ-∠λ)=-180°.【来源:21cnj*y.co*m】
二、11.【答案】105
解:在△ABC中,∠A=30°,∠B=45°,∴∠C=180°-∠A-∠B=180°-30°-45°=105°.【版权所有:21教育】
12.【答案】不可能;三角形的任何两边的和大于第三边
解:人的两腿的长度总和不可能大于5 m,故一步不可能走5 m.
13.【答案】225°
14.【答案】8
解:设这个多边形的边数为x,由题意,得(x-2)×180°=1 080°,解得x=8.
15.【答案】25°
解:∵在△ABC中,∠ACB=80°,∠B=35°,
∴∠A=180°-∠B-∠ACB=65°.∵CD⊥AB,
∴∠CDA=90°,∴∠ACD=180°-90°-65°=25°.
16.【答案】4
解:根据题意,有(n-2)·180°-(m-2)·180°=(n-m)·180°=720°,整理得n-m=4.即n与m的差为4.2-1-c-n-j-y
17.【答案】6 18.【答案】
三、19.解:①根据三角形的外角的性质,得
(x+70)°=x°+(x+10)°,解得x=60.
②根据四边形的内角和是360°,得
(x+10)°+x°+60°+90°=360°,解得x=100.
③根据五边形的内角和是(5-2)×180°=540°,
得x°+(x+20)°+(x-10)°+x°+70°=540°,
解得x=115.
20.解:如图,因为BP平分∠FBC,CP平分∠ECB,
所以∠1=∠FBC,∠2=∠ECB,
所以∠1=(∠A+∠4),∠2=(∠A+∠3),
又因为∠BPC=180°-(∠1+∠2),∠A=40°,
所以∠BPC=180°-(∠A+∠4)+(∠A+∠3)=180°-×(180°+40°)=180°-110°=70°.www-2-1-cnjy-com
解:可利用三角形外角的性质及三角形内角和为180°来求解.
21.解:都不对.锯掉一个角,可能出现如图所示的三种情况,
因此残余桌面所有的内角的和可能为540°,360°,180°.
22.解:能.设AF与BG相交于点Q,
则∠BQF=∠A+∠D+∠G,
于是∠A+∠B+∠C+∠D+∠E+∠F+∠G=
∠B+∠C+∠E+∠F+∠BQF=(5-2)×180°=540°.
23.解法一:∵∠ACB=90°,
∴∠CFE=90°-∠1,
∵CD⊥AB于D,
∴∠ADE=90°,∴∠AED=90°-∠2.
又∵AF平分∠CAB,
∴∠1=∠2,∴∠AED=∠CFE.
又∵∠CEF=∠AED(对顶角相等),
∴∠CEF=∠CFE.
解法二:∵∠ACB=90°,
∴∠ACE+∠BCD=90°.
∵CD⊥AB于D,
∴∠B+∠BCD=90°,
∴∠ACE=∠B.
∵AF平分∠CAB,
∴∠1=∠2.
∵∠CEF=∠1+∠ACE,∠CFE=∠B+∠2(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠CEF=∠CFE.
24.解:(1)正三角形的一个内角为60°,
正方形的一个内角为90°,
正六边形的一个内角为120°,
正八边形的一个内角为135°,
正十二边形的一个内角为150° .
∵60、90、120能整除360,
∴供王老师选择的正多边形地砖有正三角形地砖、正方形地砖、正六边形地砖.
(2)3×60°+2×90°=360°,∴正三角形地砖和正方形地砖可以铺满地面;2×60°+2×120°=360°或4×60°+120°=360°,∴正三角形地砖和正六边形地砖可以铺满地面;60°+2×150°=360°,∴正三角形地砖和正十二边形地砖可以铺满地面;90°+2×135°=360°,∴正方形地砖和正八边形地砖可以铺满地面,即其中任取两种组合,能铺满地面的正多边形地砖的组合有正三角形地砖和正方形地砖,正三角形地砖和正六边形地砖,正三角形地砖和正十二边形地砖,正方形地砖和正八边形地砖.【出处:21教育名师】
(3)1块正方形地砖,1块正六边形地砖,1块正十二边形地砖可以铺满地面;2块正三角形地砖,1块正方形地砖,1块正十二边形地砖可以铺满地面;1块正三角形地砖,2块正方形地砖,1块正六边形地砖可以铺满地面,∴从其中任取三种组合,能铺满地面的正多边形地砖的组合有:正三角形地砖,正方形地砖,正十二边形地砖;正方形地砖,正六边形地砖,正十二边形地砖;正三角形地砖,正方形地砖,正六边形地砖.
(4)能铺满地面的正多边形在一个顶点处的各内角的和为360°.
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的高总在三角形内部
C.三角形的高、中线、角平分线一定是三条不同的线段
D.三角形的中线在三角形内部
2.如图,AB∥CD,∠A=45°,∠C=28°, 则∠AEC的大小为( )
A.17° B.62°
C.63° D.73°
3.下列各组长度的线段,能组成三角形的是( )
A.2 cm,3 cm,4 cm B.2 cm,3 cm,5 cm
C.2 cm,5 cm,10 cm D.8 cm,4 cm,4 cm
4.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.设△ABC的三边长分别为a,b,c,其中a,b满足|a+b-4|+(a-b+2)2=0,则第三边的长c的取值范围是( )【来源:21·世纪·教育·网】
A.3
A.13 B.14 C.15 D.16
7.如图,直角三角尺的直角顶点落在直尺边上,若∠1=56°,则∠2的度数为( )
A.56° B.44° C.34° D.28°
8.等腰三角形的两边长分别为2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
9.现有四种地砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地砖铺满地面,选择的方式有( )2·1·c·n·j·y
A.2种 B.3种 C.4种 D.5种
10.如图,∠1+∠2-∠3-∠4+∠5-∠6-∠7+∠8-∠9等于( )
A.-180° B.0° C.180° D.360°
二、填空题(每题3分,共24分)
11.在△ABC中,∠A=30°,∠B=45°,则∠C=________°.?
12.有人说自己的步子大,一步能走5 m,你认为________ (填“可能”或“不可能”),用你学过的数学知识说明理21·cn·jy·com
由: .?
13.如图所示,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2=________.21·世纪*教育网
14.已知一个多边形的内角和是1 080°,则这个多边形的边数是________.?
15.如图,在△ABC中,∠ACB=80°,∠B=35°,CD⊥AB于D,则∠
ACD=________.
16.n边形与m边形内角和度数的差为720°,则n与m的差为 .?
17.用4个完全一样的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图①,用n个完全一样的正六边形按这种方式进行拼接,如图②,若围成一圈后中间形成一个正多边形,则n的值为 .21教育网
18.如图所示,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 ,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2 012BC和∠A2 012CD的平分线交于点A2 013,得∠A2 013,则∠A2 013= °.
三、解答题(23,24题每题9分,其余每题7分,共46分)
19.求出图中x的值.
20.如图所示,BP平分∠FBC,CP平分∠ECB,∠A=40°,求∠BPC的度数.
21.有一张正方形桌面,它的4个内角的和为360°,现在锯掉它的一个角,残余桌面所有的内角的和是多少?小光说:“锯掉一个角,变成三角形,于是残余桌面所有的内角的和是180°.”小欣说:“锯掉一个角,变成五边形,内角和应为540°.”你认为谁对谁不对?说说你的解答.
22.如图,请你想办法求出五角星中∠A+∠B+∠C+∠D+∠E的值.下面是习题讲解时,老师和学生对话的情境:老师向学生抛出问题:观察图①中的图形,能分别求出∠A,∠B,∠C,∠D,∠E的度数吗?能的话怎么求?不能的话怎么办?学生通过观察回答:很明显每个角都不规则,因此求不出∠A,∠B,∠C,∠D,∠E的度数.有个学生小声地说了句:要是能把这五个角放到一块就好了.老师回答:有想法,就去试试看.很快就有学生发现利用三角形外角的性质将∠C与∠E的度数和,∠B与∠D的度数和分别用∠1和∠2表示.于是得到∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.根据以上信息,你能求出图②中∠A+∠B+∠C+∠D+∠E+∠F+∠G的值吗?21世纪教育网版权所有
23.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交BC于F,试说明:∠CEF=∠CFE.21cnjy.com
24.王老师准备装修新房的地面,到一家装修公司去看地砖,该公司现有一批边长相等的正多边形地砖(如图)供客户选择.
(1)若只用其中一种正多边形地砖铺满地面,则供王老师选择的正多边形地砖有哪些?
(2)若从其中任取两种组合,能铺满地面的正多边形地砖的组合有哪些?
(3)若从其中任取三种组合,能铺满地面的正多边形地砖的组合有哪些?
(4)请说出其中所蕴含的数学道理.
参考答案
一、1.【答案】D 2.【答案】D
3.【答案】A
解:根据三角形中任意两边之和大于第三边,任意两边之差小于第三边判断.
4.【答案】A
解:设多边形的边数是n,则(n-2)·180°=360°,解得n=4.
5.【答案】D
解:∵a,b满足|a+b-4|+(a-b+2)2=0,|a+b-4|≥0,(a-b+2)2≥0,∴a+b-4=0,a-b+2=0.∴a=1,b=3.∴c的取值范围为3-1
8.【答案】C
解:本题利用分类讨论思想解题,对于已知中没有明确腰和底边的题目一定要分类讨论,还应验证各种情况是否能构成三角形,这点非常重要,也是解题的关键.21*cnjy*com
9.【答案】B
解:可选择的方式有:正三角形和正方形;正三角形和正六边形;正方形和正八边形,共3种.
10.【答案】A
解:如图,
∵∠1+∠2=180°-∠α,∠3+∠4=180°-∠γ,∠5=180°-∠γ-∠θ,∠6+∠7=180°-∠β,∠8=180°-∠β-∠λ,∠9=360°-∠α-∠θ-∠λ,∴∠1+∠2-∠3-∠4+∠5-∠6-∠7+∠8-∠9=180°-∠α-(180°-∠γ)+180°-∠γ-∠θ-(180°-∠β)+180°-∠β-∠λ-(360°-∠α-∠θ-∠λ)=-180°.【来源:21cnj*y.co*m】
二、11.【答案】105
解:在△ABC中,∠A=30°,∠B=45°,∴∠C=180°-∠A-∠B=180°-30°-45°=105°.【版权所有:21教育】
12.【答案】不可能;三角形的任何两边的和大于第三边
解:人的两腿的长度总和不可能大于5 m,故一步不可能走5 m.
13.【答案】225°
14.【答案】8
解:设这个多边形的边数为x,由题意,得(x-2)×180°=1 080°,解得x=8.
15.【答案】25°
解:∵在△ABC中,∠ACB=80°,∠B=35°,
∴∠A=180°-∠B-∠ACB=65°.∵CD⊥AB,
∴∠CDA=90°,∴∠ACD=180°-90°-65°=25°.
16.【答案】4
解:根据题意,有(n-2)·180°-(m-2)·180°=(n-m)·180°=720°,整理得n-m=4.即n与m的差为4.2-1-c-n-j-y
17.【答案】6 18.【答案】
三、19.解:①根据三角形的外角的性质,得
(x+70)°=x°+(x+10)°,解得x=60.
②根据四边形的内角和是360°,得
(x+10)°+x°+60°+90°=360°,解得x=100.
③根据五边形的内角和是(5-2)×180°=540°,
得x°+(x+20)°+(x-10)°+x°+70°=540°,
解得x=115.
20.解:如图,因为BP平分∠FBC,CP平分∠ECB,
所以∠1=∠FBC,∠2=∠ECB,
所以∠1=(∠A+∠4),∠2=(∠A+∠3),
又因为∠BPC=180°-(∠1+∠2),∠A=40°,
所以∠BPC=180°-(∠A+∠4)+(∠A+∠3)=180°-×(180°+40°)=180°-110°=70°.www-2-1-cnjy-com
解:可利用三角形外角的性质及三角形内角和为180°来求解.
21.解:都不对.锯掉一个角,可能出现如图所示的三种情况,
因此残余桌面所有的内角的和可能为540°,360°,180°.
22.解:能.设AF与BG相交于点Q,
则∠BQF=∠A+∠D+∠G,
于是∠A+∠B+∠C+∠D+∠E+∠F+∠G=
∠B+∠C+∠E+∠F+∠BQF=(5-2)×180°=540°.
23.解法一:∵∠ACB=90°,
∴∠CFE=90°-∠1,
∵CD⊥AB于D,
∴∠ADE=90°,∴∠AED=90°-∠2.
又∵AF平分∠CAB,
∴∠1=∠2,∴∠AED=∠CFE.
又∵∠CEF=∠AED(对顶角相等),
∴∠CEF=∠CFE.
解法二:∵∠ACB=90°,
∴∠ACE+∠BCD=90°.
∵CD⊥AB于D,
∴∠B+∠BCD=90°,
∴∠ACE=∠B.
∵AF平分∠CAB,
∴∠1=∠2.
∵∠CEF=∠1+∠ACE,∠CFE=∠B+∠2(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠CEF=∠CFE.
24.解:(1)正三角形的一个内角为60°,
正方形的一个内角为90°,
正六边形的一个内角为120°,
正八边形的一个内角为135°,
正十二边形的一个内角为150° .
∵60、90、120能整除360,
∴供王老师选择的正多边形地砖有正三角形地砖、正方形地砖、正六边形地砖.
(2)3×60°+2×90°=360°,∴正三角形地砖和正方形地砖可以铺满地面;2×60°+2×120°=360°或4×60°+120°=360°,∴正三角形地砖和正六边形地砖可以铺满地面;60°+2×150°=360°,∴正三角形地砖和正十二边形地砖可以铺满地面;90°+2×135°=360°,∴正方形地砖和正八边形地砖可以铺满地面,即其中任取两种组合,能铺满地面的正多边形地砖的组合有正三角形地砖和正方形地砖,正三角形地砖和正六边形地砖,正三角形地砖和正十二边形地砖,正方形地砖和正八边形地砖.【出处:21教育名师】
(3)1块正方形地砖,1块正六边形地砖,1块正十二边形地砖可以铺满地面;2块正三角形地砖,1块正方形地砖,1块正十二边形地砖可以铺满地面;1块正三角形地砖,2块正方形地砖,1块正六边形地砖可以铺满地面,∴从其中任取三种组合,能铺满地面的正多边形地砖的组合有:正三角形地砖,正方形地砖,正十二边形地砖;正方形地砖,正六边形地砖,正十二边形地砖;正三角形地砖,正方形地砖,正六边形地砖.
(4)能铺满地面的正多边形在一个顶点处的各内角的和为360°.
