5.2.2 平行线的判定 课件(38张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 课件(38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 420.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-10 08:23:12 | ||
图片预览






文档简介
课件38张PPT。5.2 平行线及其判定第五章 相交线与平行线学练优七年级数学下(RJ)
教学课件5.2.2 平行线的判定第1课时 平行线的判定学习目标1.掌握平行线的三种判定方法,会运用判定方法来判
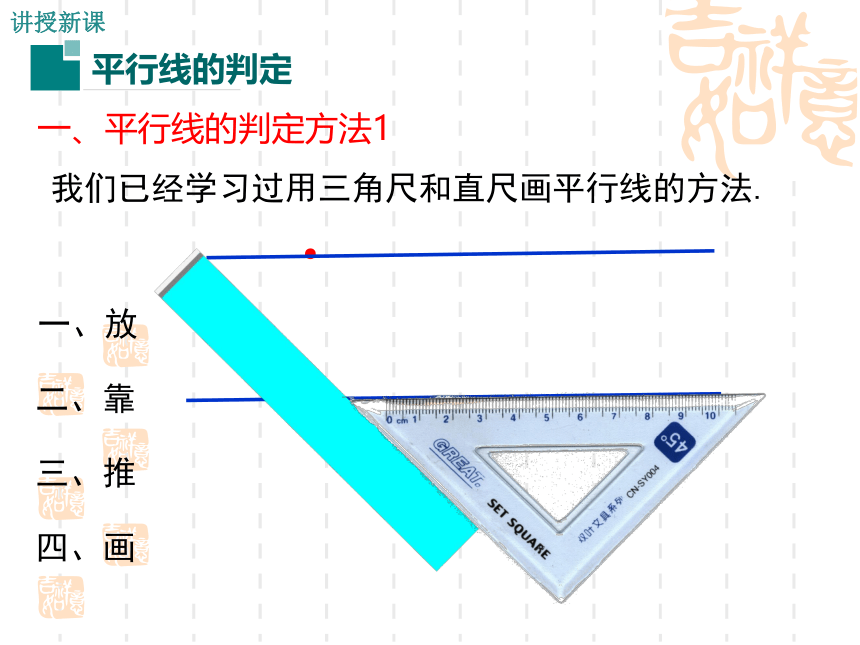
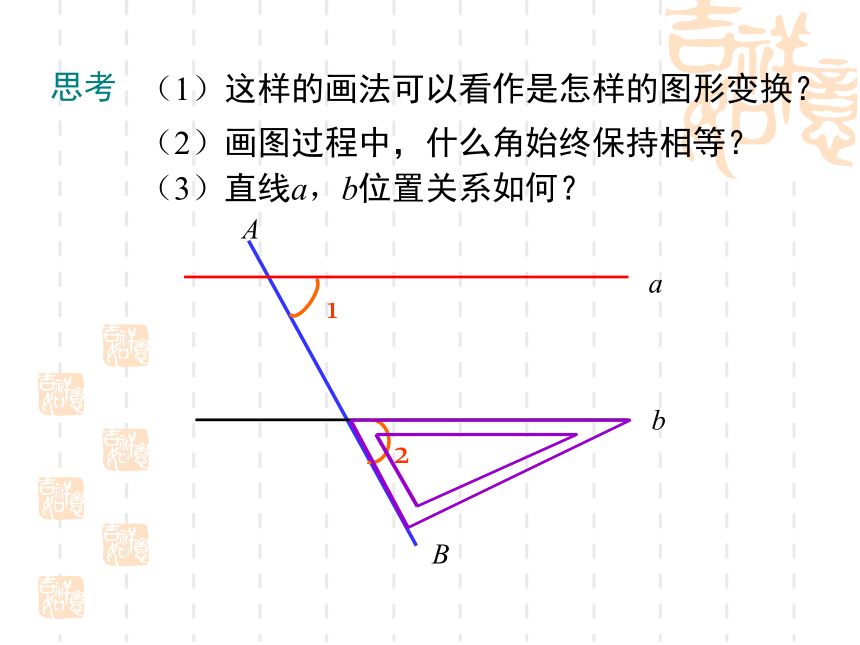
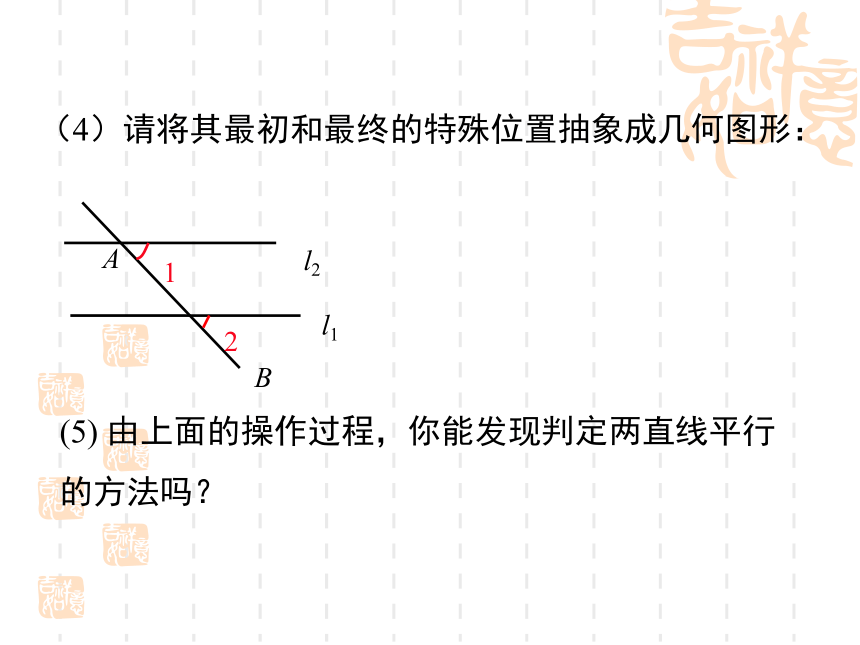
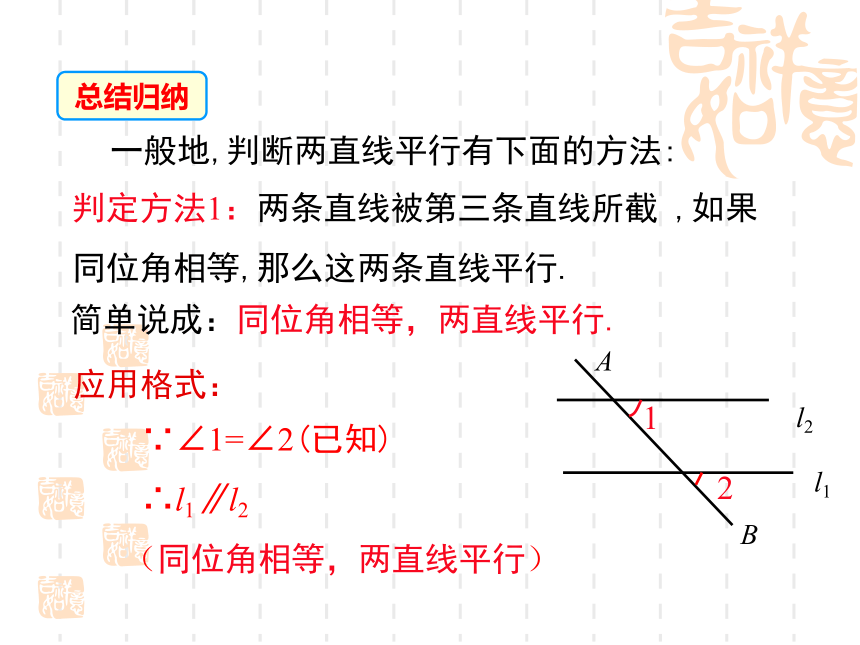
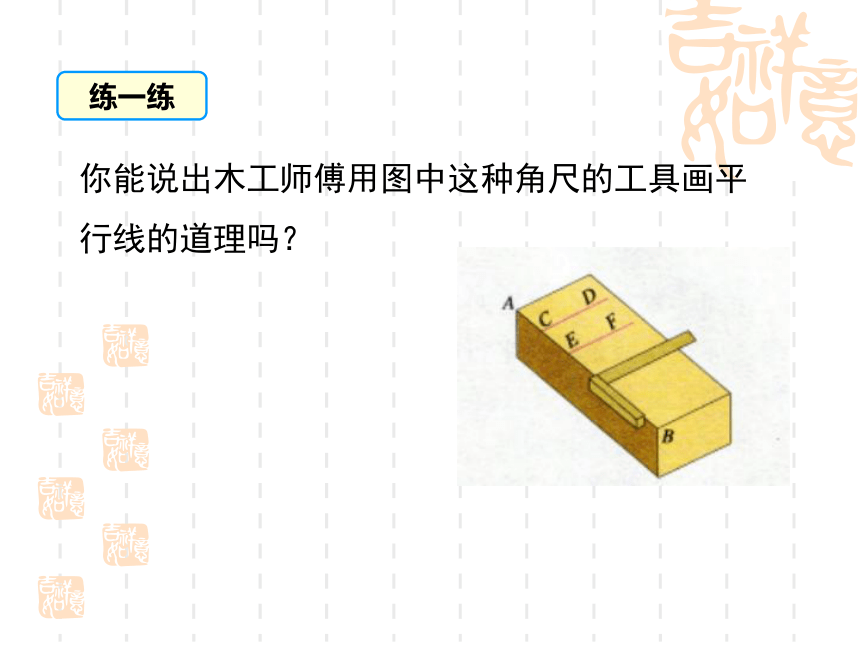
断两条 直线是否平行;(重点)2.能够根据平行线的判定方法进行简单的推理. 问题1 两条不重合的直线的位置关系有哪几种?问题2 怎样的两条直线平行?问题3 上节课你学了平行线的哪些内容?相交(包括垂直)和平行两种.在同一平面内,不相交的两条直线平行.2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.1.经过直线外一点,有且只有一条直线与已知直线平行.导入新课回顾与思考思考 根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否平行,那么有没有其他判定方法呢?●一、放二、靠三、推四、画我们已经学习过用三角尺和直尺画平行线的方法.讲授新课一、平行线的判定方法1bA21aB(1)这样的画法可以看作是怎样的图形变换? (2)画图过程中,什么角始终保持相等? (3)直线a,b位置关系如何? 思考(4)请将其最初和最终的特殊位置抽象成几何图形:(5) 由上面的操作过程,你能发现判定两直线平行的方法吗? 一般地,判断两直线平行有下面的方法:判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.应用格式: ∵∠1=∠2(已知)
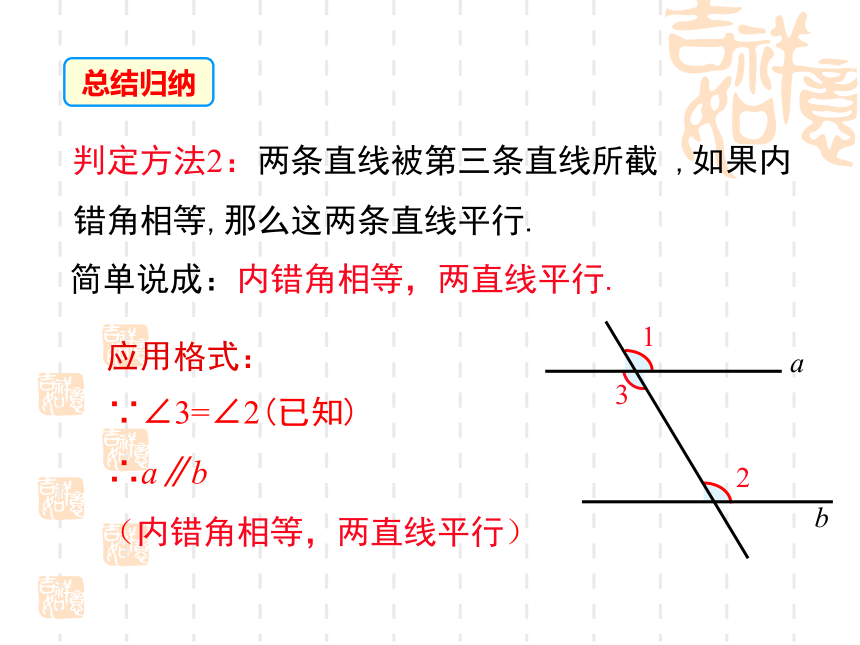
∴l1∥l2 (同位角相等,两直线平行)总结归纳你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?练一练思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?二、平行线的判定方法2如图,由?3= ?2,可推出a//b吗?如何推出?解: ∵?3= ?2 (已知)
?1=?3(对顶角相等)
? ?1= ?2
? a//b(同位角相等,两直线平行)判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)应用格式: 总结归纳如图,如果?1+?2=180° ,你能判定a//b吗?c解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角定义)
? ?2=?3(同角的补角相等)
? a//b (同位角相等,两直线平行)三、平行线的判定方法3判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.应用格式: ∵∠1+∠2=180°(已知)
∴a∥b (同旁内角互补,两直线平行)总结归纳1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠AC当堂练习2.如图,已知∠1=30°,∠2或∠3满足条件
_________ _ __,则a//b.∠2=150°或∠3=30°3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .23内错角相等,两直线平行ABC同位角相等,两直线平行 理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
4.如图,已知∠1= ∠3,AC平分∠DAB,你能判断
那两条直线平行?请说明理由?解: AB∥CD. 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°课堂小结abc12435.2 平行线及其判定第五章 相交线与平行线学练优七年级数学下(RJ)
教学课件5.2.2 平行线的判定第2课时 平行线判定方法的综合运用学习目标1.进一步掌握平行线的判定方法,并会运用平行线的
判定解决问题;(重点)2.掌握垂直于同一条直线的两条直线互相平行. 1.到目前为止,判定两直线平行的方法有哪些?(1)定义法:(这条不实用)(2)平行公理的推论:若a//b,b//c,则a//c.(3)判定方法1:同位角相等,两直线平行.(4)判定方法2:内错角相等,两直线平行.(5)判定方法3:同旁内角互补,两直线平行.导入新课复习导入2.下面的题你会吗?如果会,请说说你的理由.若∠1=∠2,则b c.若∠1=∠2,则 // .若∠ =∠ ,则AB//DC.//ADBC23(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?例1 如图,E是AB上一点,F是DC上一点,G是BC延长线
上一点.(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?解 (1)AB//CD, 同位角相等,两直线平行; (2)AD//BC, 内错角相等,两直线平行; (3)AD//EF, 同旁内角互补,两直线平行.讲授新课例2 如图,为了说明示意图中的平安大街与长安街
是互相平行的,在地图上量得∠1=90°,你能通过
度量图中已标出的其他的角来验证这个结论吗?
说出你的理由.解:验证方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
验证方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
验证方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
(答案不唯一)例3 如图,∠1=∠2,能判断AB∥DF吗?为什么??
?
?
?
?
?解:不能.添加∠CBD=∠EDB内错角相等,两直线平行想想还可以添加什么条件?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么??垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)你还能利用其他方法说明b//c吗? 若∠3=__,即∠1+ ∠3=180o,则AB//CD.
( )1.如图,直线AB,CD被直线EF所截 .
若∠1=120o,∠2= __ ,则AB//CD.
( )内错角相等,两直线平行120o60o同旁内角互补,两直线平行当堂练习2.用两块相同的三角板按如图所示的方式作平
行线,能解释其中道理是什么?解:内错角相等,两直线平行3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )A.第一次向右拐50o,第二次向左拐130o
B.第一次向左拐30o,第二次向右拐30o
C.第一次向右拐50o,第二次向右拐130o
D.第一次向左拐50o,第二次向左拐130oB4.(1)∵∠1=∠4,(已知)
∴ ∥ .( )(2)∵∠ABC +∠ =180o,(已知)
∴AB∥CD.( )ABCDBCD内错角相等,两直线平行同旁内角互补,两直线平行(3)∵∠ =∠ (已知)
∴AD∥BC( )(4)∵∠5=∠ (已知)
∴AB∥CD( )32ABC内错角相等,两直线平行同位角相等,两直线平行31
解析:根据平行线的判定定理即可求得答案.
①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥BC;
③∵∠3=∠4,∴AB∥CD;
④∵∠B=∠5,∴AB∥CD.
∴能得到AB∥CD的条件是①③④.故选C.5.如图,有以下四个条件:①∠B+∠BCD=180°;
②∠1=∠2;③∠3=∠4;④∠B=∠5,其中能
判定AB∥CD的条件有( )A.1个 B.2个 C.3个 D.4个
245C拓展提升:
(1)如图1,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.解:∠3=∠2=55°,AB∥CD(2)如图2,∠1=55°,∠2=125°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
解:∠3=180°-∠1=125°,AB∥CD1.在使用平行线的判定方法时,要明确以下两点: (1)各判定方法的条件是什么,结论是什么. (2)判定方法已知的是角的关系,说明的是两
直线平行.2.在使用平行线的判定方法时,碰到复杂图形要会
从其中分离出基本图形.
课堂小结3.在同一平面内,垂直于同一条直线的两条直线平行.
教学课件5.2.2 平行线的判定第1课时 平行线的判定学习目标1.掌握平行线的三种判定方法,会运用判定方法来判
断两条 直线是否平行;(重点)2.能够根据平行线的判定方法进行简单的推理. 问题1 两条不重合的直线的位置关系有哪几种?问题2 怎样的两条直线平行?问题3 上节课你学了平行线的哪些内容?相交(包括垂直)和平行两种.在同一平面内,不相交的两条直线平行.2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.1.经过直线外一点,有且只有一条直线与已知直线平行.导入新课回顾与思考思考 根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否平行,那么有没有其他判定方法呢?●一、放二、靠三、推四、画我们已经学习过用三角尺和直尺画平行线的方法.讲授新课一、平行线的判定方法1bA21aB(1)这样的画法可以看作是怎样的图形变换? (2)画图过程中,什么角始终保持相等? (3)直线a,b位置关系如何? 思考(4)请将其最初和最终的特殊位置抽象成几何图形:(5) 由上面的操作过程,你能发现判定两直线平行的方法吗? 一般地,判断两直线平行有下面的方法:判定方法1:两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.应用格式: ∵∠1=∠2(已知)
∴l1∥l2 (同位角相等,两直线平行)总结归纳你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?练一练思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?二、平行线的判定方法2如图,由?3= ?2,可推出a//b吗?如何推出?解: ∵?3= ?2 (已知)
?1=?3(对顶角相等)
? ?1= ?2
? a//b(同位角相等,两直线平行)判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)应用格式: 总结归纳如图,如果?1+?2=180° ,你能判定a//b吗?c解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角定义)
? ?2=?3(同角的补角相等)
? a//b (同位角相等,两直线平行)三、平行线的判定方法3判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.应用格式: ∵∠1+∠2=180°(已知)
∴a∥b (同旁内角互补,两直线平行)总结归纳1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠AC当堂练习2.如图,已知∠1=30°,∠2或∠3满足条件
_________ _ __,则a//b.∠2=150°或∠3=30°3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行(3)从∠ =∠ ,可以推出AD∥BC,
理由是 .(4)从∠5=∠ ,可以推出AB∥CD,
理由是 .23内错角相等,两直线平行ABC同位角相等,两直线平行 理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
4.如图,已知∠1= ∠3,AC平分∠DAB,你能判断
那两条直线平行?请说明理由?解: AB∥CD. 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°课堂小结abc12435.2 平行线及其判定第五章 相交线与平行线学练优七年级数学下(RJ)
教学课件5.2.2 平行线的判定第2课时 平行线判定方法的综合运用学习目标1.进一步掌握平行线的判定方法,并会运用平行线的
判定解决问题;(重点)2.掌握垂直于同一条直线的两条直线互相平行. 1.到目前为止,判定两直线平行的方法有哪些?(1)定义法:(这条不实用)(2)平行公理的推论:若a//b,b//c,则a//c.(3)判定方法1:同位角相等,两直线平行.(4)判定方法2:内错角相等,两直线平行.(5)判定方法3:同旁内角互补,两直线平行.导入新课复习导入2.下面的题你会吗?如果会,请说说你的理由.若∠1=∠2,则b c.若∠1=∠2,则 // .若∠ =∠ ,则AB//DC.//ADBC23(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?例1 如图,E是AB上一点,F是DC上一点,G是BC延长线
上一点.(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?解 (1)AB//CD, 同位角相等,两直线平行; (2)AD//BC, 内错角相等,两直线平行; (3)AD//EF, 同旁内角互补,两直线平行.讲授新课例2 如图,为了说明示意图中的平安大街与长安街
是互相平行的,在地图上量得∠1=90°,你能通过
度量图中已标出的其他的角来验证这个结论吗?
说出你的理由.解:验证方法1:测出∠3=90°,
理由是同位角相等,两直线平行.
验证方法2:测出∠2=90°,
理由是同旁内角互补,两直线平行.
验证方法3:测出∠5=90°,
理由是内错角相等,两直线平行.
(答案不唯一)例3 如图,∠1=∠2,能判断AB∥DF吗?为什么??
?
?
?
?
?解:不能.添加∠CBD=∠EDB内错角相等,两直线平行想想还可以添加什么条件?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.思考:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么??垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)你还能利用其他方法说明b//c吗? 若∠3=__,即∠1+ ∠3=180o,则AB//CD.
( )1.如图,直线AB,CD被直线EF所截 .
若∠1=120o,∠2= __ ,则AB//CD.
( )内错角相等,两直线平行120o60o同旁内角互补,两直线平行当堂练习2.用两块相同的三角板按如图所示的方式作平
行线,能解释其中道理是什么?解:内错角相等,两直线平行3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )A.第一次向右拐50o,第二次向左拐130o
B.第一次向左拐30o,第二次向右拐30o
C.第一次向右拐50o,第二次向右拐130o
D.第一次向左拐50o,第二次向左拐130oB4.(1)∵∠1=∠4,(已知)
∴ ∥ .( )(2)∵∠ABC +∠ =180o,(已知)
∴AB∥CD.( )ABCDBCD内错角相等,两直线平行同旁内角互补,两直线平行(3)∵∠ =∠ (已知)
∴AD∥BC( )(4)∵∠5=∠ (已知)
∴AB∥CD( )32ABC内错角相等,两直线平行同位角相等,两直线平行31
解析:根据平行线的判定定理即可求得答案.
①∵∠B+∠BCD=180°,∴AB∥CD;
②∵∠1=∠2,∴AD∥BC;
③∵∠3=∠4,∴AB∥CD;
④∵∠B=∠5,∴AB∥CD.
∴能得到AB∥CD的条件是①③④.故选C.5.如图,有以下四个条件:①∠B+∠BCD=180°;
②∠1=∠2;③∠3=∠4;④∠B=∠5,其中能
判定AB∥CD的条件有( )A.1个 B.2个 C.3个 D.4个
245C拓展提升:
(1)如图1,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.解:∠3=∠2=55°,AB∥CD(2)如图2,∠1=55°,∠2=125°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
解:∠3=180°-∠1=125°,AB∥CD1.在使用平行线的判定方法时,要明确以下两点: (1)各判定方法的条件是什么,结论是什么. (2)判定方法已知的是角的关系,说明的是两
直线平行.2.在使用平行线的判定方法时,碰到复杂图形要会
从其中分离出基本图形.
课堂小结3.在同一平面内,垂直于同一条直线的两条直线平行.
