9.2.1 一元一次不等式的解法 课件

课件16张PPT。第九章 不等式与不等式组9.2 一元一次不等式1 一元一次不等式的解法1.理解和掌握一元一次不等式的概念；
2.会用不等式的性质熟练地解一元一次不等式.(重点、
难点）学习目标导入新课 已知一台升降机的最大载重量是1200kg，在
一名重75kg的工人乘坐的情况下，它最多能装载
多少件25kg重的货物？观察与思考前面问题中涉及的数量关系是： 设能载x件25kg重的货物，因为升降机最大载重量是1200kg，所以有
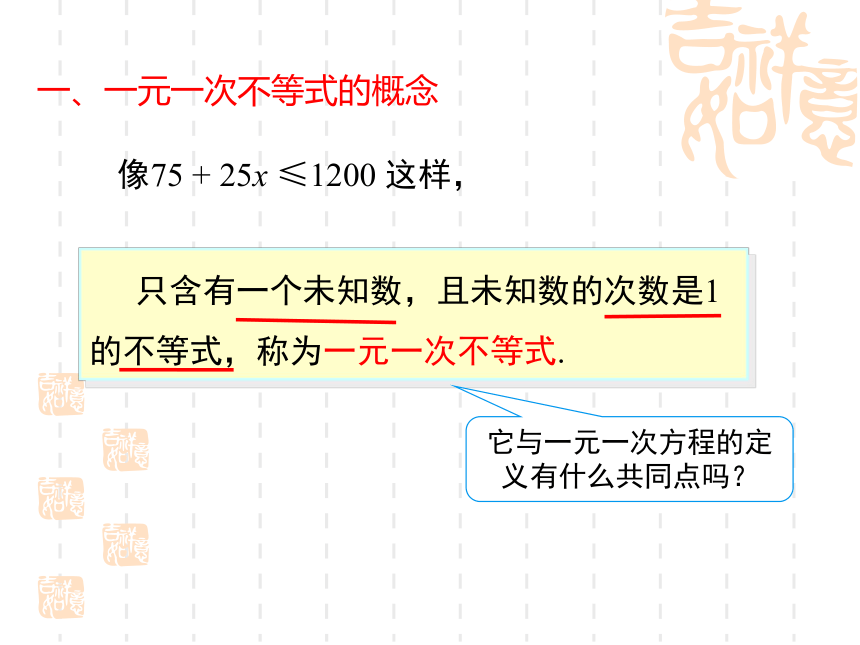
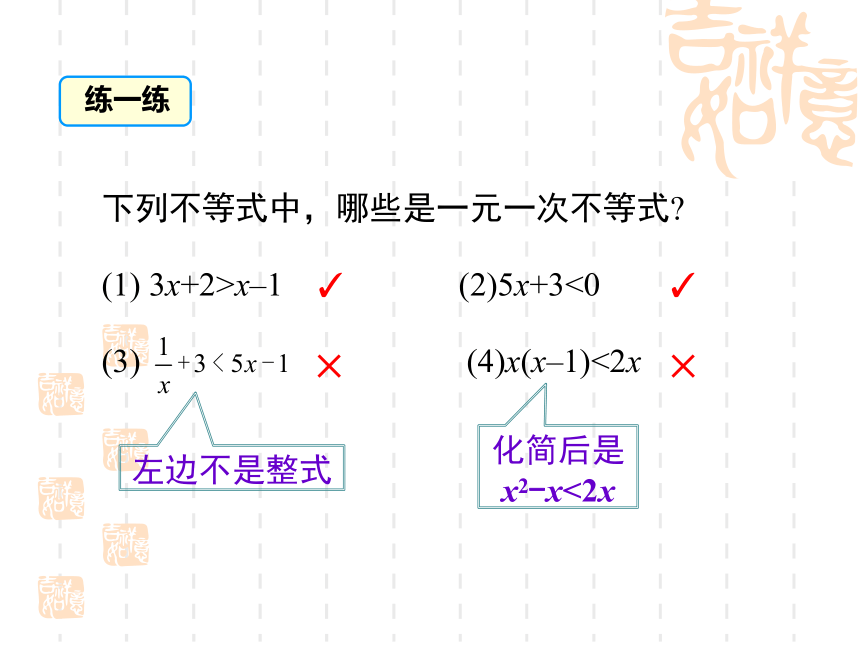
75＋25x≤1200. ①工人重 + 货物重 ≤ 最大载重量.讲授新课 只含有一个未知数，且未知数的次数是1的不等式，称为一元一次不等式.像75 + 25x ≤1200 这样，它与一元一次方程的定义有什么共同点吗？一、一元一次不等式的概念下列不等式中，哪些是一元一次不等式?
(1) 3x+2>x–1 (2)5x+3<0
(3) (4)x(x–1)<2x????左边不是整式化简后是
x2-x<2x 为了求出升降机能装载货物的件数，需要求出满足不等式75＋25x≤1200的x的值.如何求呢？ 与解一元一次方程类似，我们将根据不等式的基本性质，进行如下步骤：将不等式75+25x≤1200移项，得将②式两边都除以25（即将x的系数化为1）， 25x ≤ 1125. ②得 x≤45.因此，升降机最多装载45件25kg重的货物. 今后我们在解一元一次不等式时，将利用前面讲述的不等式的基本性质，将原不等式化成形如x ≤a(或xa，x≥a）的不等式，就可得到原不等式的解集. 这个求不等式的解集的过程称为解不等式.二、解不等式的概念例1 解下列一元一次不等式 ：（1） 2-5x < 8-6x ；（2） .解：（1） 原不等式为2-5x < 8-6x 将同类项放在一起即 x < 6. 移项，得 -5x+6x < 8-2，计算结果典例精析解：首先将分母去掉去括号，得 2x-10+6≤9x 去分母，得 2(x-5)+1×6≤9x移项，得 2x-9x≤10-6去括号将同类项放在一起合并同类项，得 -7x ≤4 两边都除以-7，得计算结果根据不等式性质3例2 解不等式12-6x≥2(1-2x)，并把它的解集在数轴
上表示出来.解：首先将括号去掉去括号，得 12-6x ≥2-4x移项，得 -6x+4x ≥ 2-12将同类项放在一起合并同类项，得 -2x ≥-10两边都除以-2，得 x ≤ 5根据不等式基本性质3原不等式的解集在数轴上表示如图所示.注：解集x≤5中包含5，所以在数轴上将表示5的点画成实心圆点. 解一元一次不等式与解一元一次方程的依据和步骤有什么异同点？ 它们的依据不相同.解一元一次方程的依据是等式的性质，解一元一次不等式的依据是不等式的性质. 它们的步骤基本相同，都是去分母、去括号、移项、合并同类项、未知数的系数化为1. 这些步骤中，要特别注意的是：不等式两边都乘（或除以）同一个负数，必须改变不等号的方向.这是与解一元一次方程不同的地方.当堂练习 1. 解下列不等式：3. 解下列不等式，并把它们的解集在数轴上表示出来：解：(1)原不等式的解集为x<5，在数轴上表示为 (2)原不等式的解集为x≤-11，在数轴上表示为：课堂小结一元一次不等式一元一次不等式的概念步骤解一元一次不等式→