九年级数学下册 28.2.2 解直角三角形及应用特色训练1(含答案)
文档属性
| 名称 | 九年级数学下册 28.2.2 解直角三角形及应用特色训练1(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-10 11:38:16 | ||
图片预览


文档简介
28.2.2
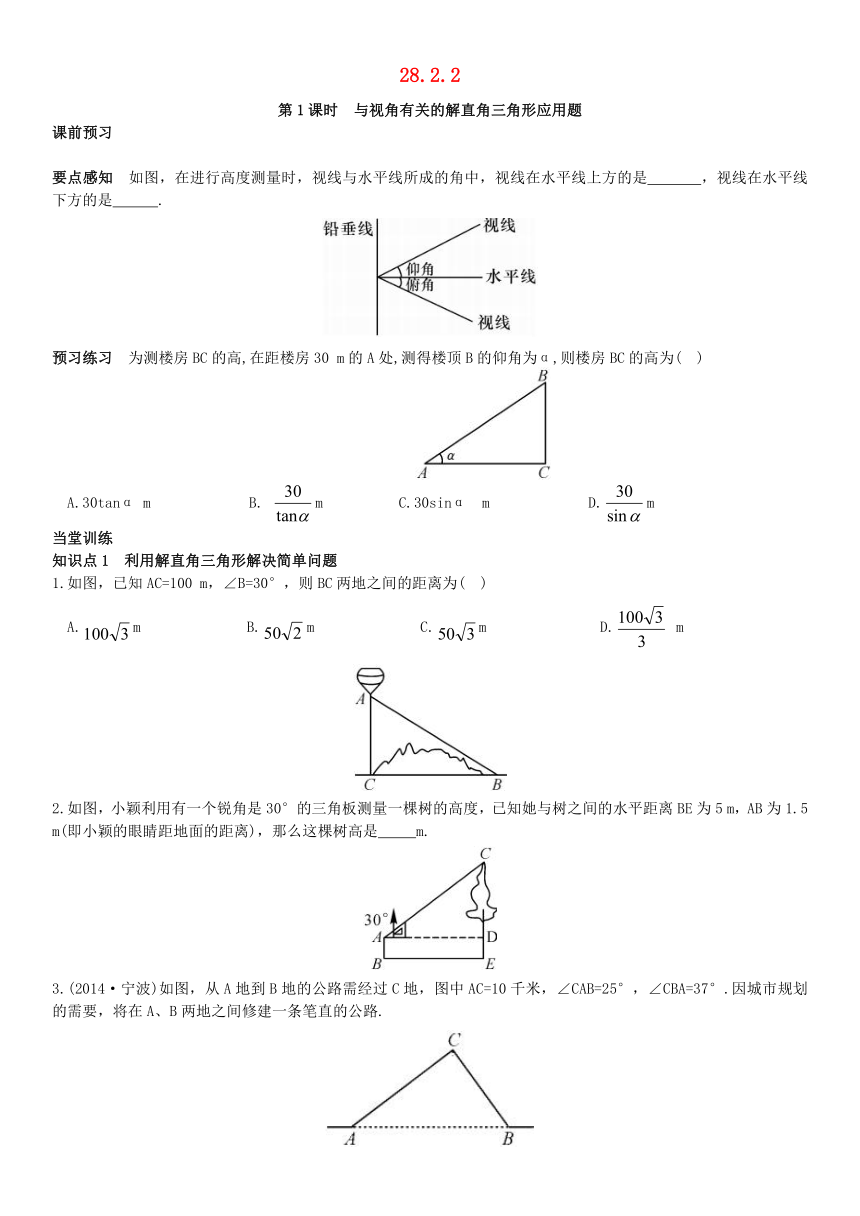
第1课时
与视角有关的解直角三角形应用题
课前预习
要点感知
如图,在进行高度测量时,视线与水平线所成的角中,视线在水平线上方的是
,视线在水平线下方的是
.
( http: / / www.21cnjy.com )
预习练习
为测楼房BC的高,在距楼房30
m的A处,测得楼顶B的仰角为α,则楼房BC的高为(
)
( http: / / www.21cnjy.com )
A.30tanα
m
B.
m
C.30sinα
m
D.m
当堂训练
知识点1
利用解直角三角形解决简单问题
1.如图,已知AC=100
m,∠B=30°,则BC两地之间的距离为(
)
A.m
B.m
C.m
D.
m
( http: / / www.21cnjy.com )
2.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5
m,AB为1.5
m(即小颖的眼睛距地面的距离),那么这棵树高是
m.
( http: / / www.21cnjy.com )
3.(2014·宁波)如图,从A地到B地
( http: / / www.21cnjy.com )的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
( http: / / www.21cnjy.com )
(1)求改直后的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
知识点2
利用视角解直角三角形
4.(2014·株洲)孔明同学在距某电视塔
( http: / / www.21cnjy.com )塔底水平距离500米处,看塔顶的仰角为20°(不考虑身高因素),则此塔高约为
米.(结果保留整数,参考数据:sin20°≈0.342
0,sin70°≈0.939
7,tan20°≈0.364
0,tan70°≈2.747
5)
( http: / / www.21cnjy.com )
5.(2014·广东)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10
m,到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度.(结果精确到0.1
m)(参考数据:≈1.414,≈1.732)
( http: / / www.21cnjy.com )
课后作业
6.(2014·枣庄)如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30
cm.
( http: / / www.21cnjy.com )
(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到1
cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.
57,tan55°≈1.43)
(2014·内江)“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机现测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点.此时测得点F在点B俯角为45°的方向上.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:≈1.7)
( http: / / www.21cnjy.com )
8.(2014·自贡)如图,某学校新建了一座吴玉章雕塑,小林站在距离2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:=1.7)
( http: / / www.21cnjy.com )
挑战自我
9.(2014·潍坊)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1
100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
( http: / / www.21cnjy.com )
参考答案
课前预习
要点感知
仰角
俯角
预习练习
A
当堂训练
1.A
2.+
3.(1)作CH⊥AB于点H.
在Rt△ACH中,
CH=AC·sin∠CAB=AC·sin25°≈4.2,
AH=AC·cos∠CAB=AC·cos25°≈9.1.
在Rt△BCH中,BH=CH÷tan37°≈5.6.
∴AB=AH+BH=9.1+5.6=14.7(千米).
(2)BC=CH÷sin37°≈7.0,
∴AC+BC-AB=10+7-14.7=2.3(千米).
答:公路改直后比原来缩短了2.3千米.
4.182
5.∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD-∠A=60°-30°=30°,
∴∠A=∠ACB.
∴BC=AB=10米.
在Rt△BCD中,CD=BCsin∠CBD=10×=5≈5×1.732≈8.7(米).
答:这棵树CD的高度为8.7米.
课后作业
6.(1)在Rt△BOE中,OE=,
在Rt△BDE中,DE=,
则+=30,解得BE≈10.6.
故B点到OP的距离大约为11
cm;
(2)在Rt△BDE中,BD=≈25.3
cm.
答:滑动支架的长为25
cm.
7.由题意知∠CBF=45°,∠BCF=90°,
∴CF=CB.
∵∠A=30°,
∴tan30°===.
∵AB=800,
∴=,
∴CF=400(+1)≈1
080.
答:竖直高度CF约为1
080米.
8.过B点作BE⊥DC于E点,
∵BA⊥AF,DF⊥AF,
∴四边形ABEF为矩形,BE=2.7.
在Rt△BEC中,∠CBE=30°,tan∠CBE=,
∴CE=BE·tan30°=.
在Rt△BDE中,∠DBE=45°,BE=2.7,
∴DE=2.7,
DC=2.7-≈1.2.
答:塑像CD的高度约为1.2米.
9.过点A作AE⊥CD于点E,过点B作BF⊥CD,交CD的延长线于点F,则四边形ABFE为矩形,
∴AB=EF,AE=BF.
由题意可知AE=BF=1
100-200=900(米),CD=19
900米.
在Rt△AEC中,∠C=45°,AE=900米,
∴CE===900(米).
在Rt△BFD中,∠BDF=60°,BF=90°,BF=900米,
∴DF===300(米).
∴AB=EF=CD+DF-CE=19
900+300-900=(19
000+300)米.
答:两海岛之间的距离AB是(19
000+300)米.
第1课时
与视角有关的解直角三角形应用题
课前预习
要点感知
如图,在进行高度测量时,视线与水平线所成的角中,视线在水平线上方的是
,视线在水平线下方的是
.
( http: / / www.21cnjy.com )
预习练习
为测楼房BC的高,在距楼房30
m的A处,测得楼顶B的仰角为α,则楼房BC的高为(
)
( http: / / www.21cnjy.com )
A.30tanα
m
B.
m
C.30sinα
m
D.m
当堂训练
知识点1
利用解直角三角形解决简单问题
1.如图,已知AC=100
m,∠B=30°,则BC两地之间的距离为(
)
A.m
B.m
C.m
D.
m
( http: / / www.21cnjy.com )
2.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5
m,AB为1.5
m(即小颖的眼睛距地面的距离),那么这棵树高是
m.
( http: / / www.21cnjy.com )
3.(2014·宁波)如图,从A地到B地
( http: / / www.21cnjy.com )的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
( http: / / www.21cnjy.com )
(1)求改直后的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
知识点2
利用视角解直角三角形
4.(2014·株洲)孔明同学在距某电视塔
( http: / / www.21cnjy.com )塔底水平距离500米处,看塔顶的仰角为20°(不考虑身高因素),则此塔高约为
米.(结果保留整数,参考数据:sin20°≈0.342
0,sin70°≈0.939
7,tan20°≈0.364
0,tan70°≈2.747
5)
( http: / / www.21cnjy.com )
5.(2014·广东)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10
m,到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度.(结果精确到0.1
m)(参考数据:≈1.414,≈1.732)
( http: / / www.21cnjy.com )
课后作业
6.(2014·枣庄)如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30
cm.
( http: / / www.21cnjy.com )
(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到1
cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.
57,tan55°≈1.43)
(2014·内江)“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机现测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点.此时测得点F在点B俯角为45°的方向上.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:≈1.7)
( http: / / www.21cnjy.com )
8.(2014·自贡)如图,某学校新建了一座吴玉章雕塑,小林站在距离2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:=1.7)
( http: / / www.21cnjy.com )
挑战自我
9.(2014·潍坊)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1
100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
( http: / / www.21cnjy.com )
参考答案
课前预习
要点感知
仰角
俯角
预习练习
A
当堂训练
1.A
2.+
3.(1)作CH⊥AB于点H.
在Rt△ACH中,
CH=AC·sin∠CAB=AC·sin25°≈4.2,
AH=AC·cos∠CAB=AC·cos25°≈9.1.
在Rt△BCH中,BH=CH÷tan37°≈5.6.
∴AB=AH+BH=9.1+5.6=14.7(千米).
(2)BC=CH÷sin37°≈7.0,
∴AC+BC-AB=10+7-14.7=2.3(千米).
答:公路改直后比原来缩短了2.3千米.
4.182
5.∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD-∠A=60°-30°=30°,
∴∠A=∠ACB.
∴BC=AB=10米.
在Rt△BCD中,CD=BCsin∠CBD=10×=5≈5×1.732≈8.7(米).
答:这棵树CD的高度为8.7米.
课后作业
6.(1)在Rt△BOE中,OE=,
在Rt△BDE中,DE=,
则+=30,解得BE≈10.6.
故B点到OP的距离大约为11
cm;
(2)在Rt△BDE中,BD=≈25.3
cm.
答:滑动支架的长为25
cm.
7.由题意知∠CBF=45°,∠BCF=90°,
∴CF=CB.
∵∠A=30°,
∴tan30°===.
∵AB=800,
∴=,
∴CF=400(+1)≈1
080.
答:竖直高度CF约为1
080米.
8.过B点作BE⊥DC于E点,
∵BA⊥AF,DF⊥AF,
∴四边形ABEF为矩形,BE=2.7.
在Rt△BEC中,∠CBE=30°,tan∠CBE=,
∴CE=BE·tan30°=.
在Rt△BDE中,∠DBE=45°,BE=2.7,
∴DE=2.7,
DC=2.7-≈1.2.
答:塑像CD的高度约为1.2米.
9.过点A作AE⊥CD于点E,过点B作BF⊥CD,交CD的延长线于点F,则四边形ABFE为矩形,
∴AB=EF,AE=BF.
由题意可知AE=BF=1
100-200=900(米),CD=19
900米.
在Rt△AEC中,∠C=45°,AE=900米,
∴CE===900(米).
在Rt△BFD中,∠BDF=60°,BF=90°,BF=900米,
∴DF===300(米).
∴AB=EF=CD+DF-CE=19
900+300-900=(19
000+300)米.
答:两海岛之间的距离AB是(19
000+300)米.
